基于快速聚类-信息量模型的汶川及周边两县滑坡易发性评价

周天伦，曾 超，范 晨，毕鸿基，龚恩慧，刘 晓

（1.中国地质大学（武汉）教育部长江三峡库区地质灾害研究中心，湖北 武汉 430074；2.中交第二公路勘察设计研究院有限公司，湖北 武汉 430056）

0 引言

滑坡是我国频发的一种地质灾害，不仅给人类生命安全带来威胁，而且对财产、环境、资源等具有破坏性[1]。面对严峻的滑坡灾害，传统的面向单体滑坡的预测研究已显得力不从心,区域性的、超前性的预测研究迫在眉睫[1]。近年涌现了大量区域滑坡易发性评价方法，如国外学者LEE等[2]使用频率比法和逻辑回归模型对马来西亚雪兰莪州进行了滑坡敏感性评价，并对两种模型做出比较评价；POURGHASEMI等[3]运用支持向量机法对伊朗戈勒斯坦省滑坡易发性做出了评价。国内学者DU等[4]结合遥感数据集与启发式易发性模型和统计学易发性模型，克服了滑坡数据空间覆盖有限和滑坡解译不确定性的问题；高克昌等[5]应用信息量模型对重庆万州区进行滑坡易发性区划；刘艺梁等[6]运用逻辑回归模型和人工神经网络模型（Artificial Neural Network，ANN）对三峡坝区东段进行滑坡易发性研究，并对两种模型进行比较分析。

汶川地震后，随着研究的深入，JIANG等[7]、马国超[8]和王磊[9]对汶川县及周边县滑坡灾害分布做出了研究和评价，总体技术路线是：基于收集的滑坡数据，选取影响滑坡发生的影响因子，以各二级因子为输入，通过特定的评价模型在GIS平台上进行栅格运算，得出易发性分区图。其中，对各个影响因子再次进行分级，以形成二级因子的过程是关键步骤之一。但现有文献对此的处理通常要么基于难以把握的主观判断[10−11]，要么基于武断的等距分级等方法[12−14]，因而忽视了二级因子本身所承载的内在聚类的特异性。

鉴于此，本文对传统等距分类方法进行改进，提出一种“快速聚类-信息量模型”。该模型通过对二级因子的分类优化，以及对滑坡样本实际面积的考虑，提高了汶川及周边两县的滑坡易发性评价精度，为该区域滑坡地质灾害的防控提供了参考。

1 研究方法

文章致力于提出“快速聚类-信息量模型”，其特色在于：第一，采用快速聚类法对生成信息量模型所需的二级评价因子进行分类；第二，考虑滑坡样本的实际面积对信息量模型的影响。基于上述两项特色，与常规的处理方案（等距分类、不考虑滑坡面积）展开对比分析，探究滑坡规模对滑坡区域易发性评价的影响，总体技术路线见图1。首先，以汶川及周边两县（理县和茂县）为研究区，从截至2020年发生的176个历史滑坡点随机抽取159处作为训练样本，剩余17处作为验证样本；然后选定7个影响因子，结合快速聚类法对各因子进行分级，采用信息量模型生成滑坡灾害易发性区划图；最后，利用线下面积（Area Under Curve，AUC）以及17处验证滑坡点的分布等指标，与常规的二级因子等距分类方案所得结果进行对比，评价两者的预测精度。

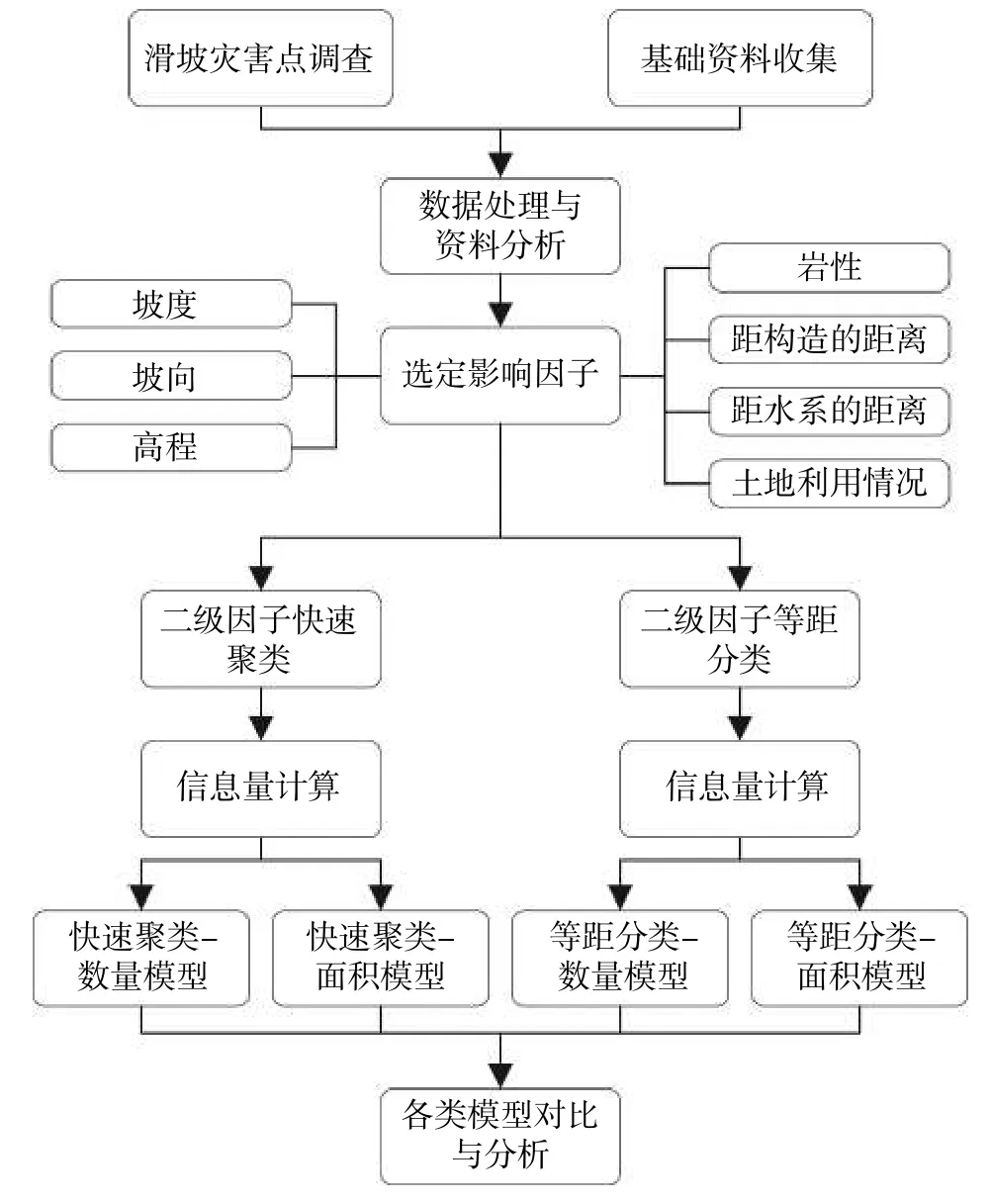
图1 技术路线图Fig.1 Technology road mapping

1.1 信息量模型

1.1.1 理论基础

信息量法的理论依据主要是信息论和工程类比法，应用于滑坡易发性评价是通过统计分析历史已发生的滑坡分布资料和导致滑坡发生的影响因子的实际数据来计算影响因子的信息量值。简而言之，就是从研究区已发生的滑坡实际情况出发，把影响滑坡发育的各因子的实测值转化为影响滑坡易发性的信息量值[13]。按式(1)分别计算各因素xi对滑坡发生事件H提供的信息量，记为I(xi,H)[5]。

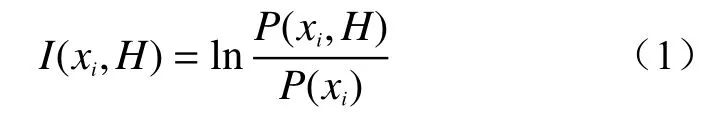
式中：P(xi,H)——滑坡发生情况下出现因子xi的概率；

H——滑坡发生事件；

P(xi)——区域内因子xi出现的概率。

1.1.2 基于滑坡样本点数的信息量模型

式(1)仅是理论模型，在实际应用中常使用样本频率计算：

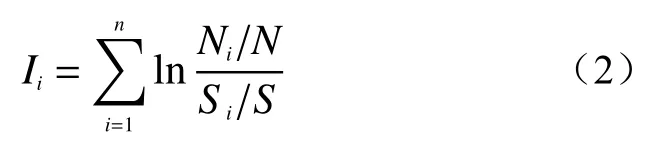
式中：Ii——评价单元总信息量；

Ni——xi因子区域内发生的滑坡数；

N——全区发生滑坡总数；

Si——全区含有xi因子所占面积；

S——全区总面积；

n——影响因子数。

1.1.3 基于滑坡样本面积的信息量模型

滑坡是具有实际空间体积与位置的空间体，所以单纯考虑滑坡点数量的信息量模型忽视了滑坡体规模对于信息量的影响，故对上述信息量模型的式(2)进行修改：

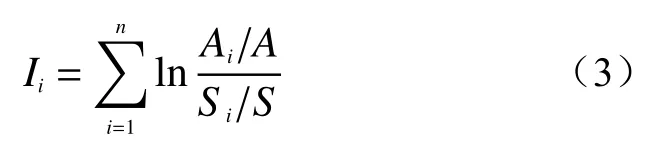
式中：Ai——xi因子区域内发生的滑坡面积；

A——全区发生滑坡总面积。

1.2 快速聚类法（K-means聚类）

1.2.1 快速聚类与等距分类的区别

聚类是一个将数据集划分为若干个子集的过程，并使得同一集合内的数据对象具有较高的相似度，而不同集合中的数据对象则是不相似的，相似或不相似的度量是基于数据对象描述属性的取值来确定的，通常就是利用各个聚类间的距离来进行描述[15]。其中快速聚类法是聚类分析中的方法之一，其核心思想是通过对聚类中心的迭代更新，将N个样本会分在K个类别中，并保证每个数据到对应聚类中心的距离（误差）平方和最小，从而保证各数据组内尽量相似，组间相似性尽可能小。该方法并不需要事先知晓各个类别的具体划分，属于无监督学习。

分类不同于聚类，分类是指在已知数据集类别标号的情况下将各数据分别属于哪一类标记出来，这是一种监督学习的过程，故而等距分类法所隐含的逻辑是假设样本对于某一特征符合均匀分布，然而这一隐含假设在多数情况下并不能严格满足。也就是说，对于指定的影响因子，实际发生的滑坡在影响因子值域中的分布并不均匀。因此，等距分类会因不符合实际情况而引入较大误差，经过复杂的系统误差传递、甚至放大等过程影响到最终的易发性评价结果。

快速聚类法区别于等距分类方法存在割裂样本内在聚类的特异性等缺点，其有着不需要事先知晓样本类别标签，仅通过组内类别中心的迭代更新以达到将样本按照组内尽量相似，组间相似度尽可能小的方式分类的优点。且该方法具有易于描述、计算效率高且适于处理大规模数据等优点，自20世纪70年代以来，该算法在国内外已经被应用到包括自然语言处理、土壤、考古等众多领域[16]。

1.2.2 快速聚类法的理论及应用

分类时应用“欧式距离法”和就近原则确定聚类中心和样本所属类别，通过多次迭代聚类中心不再移动后完成分类，每个定量因子聚类流程如图2所示。具体公式如下：

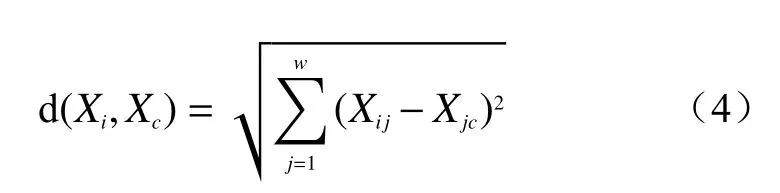
式中：Xi——样本i（i=1,2,3,···,Q），Q为样本个数；

Xc——样本总体聚类中心（c=1,2,3，···，K），K为聚类数；

w——样本Xi属性指标个数；

Xij——样本Xi的j属性指标值；

Xjc——指标属性j的聚类中心（c=1,2,3,···,K）；

d(Xi，Xc)——样本Xi关于聚类中心Xc的欧氏距离。

样本Xi经过式(4)计算后，按照就近原则（距离聚类中心最近）将样本分为K类。之后计算各组内样本平均值作为新的聚类中心，并重新计算样本与聚类中心的距离，然后更新分类，直至聚类中心不发生变化后，聚类结束，新的聚类中心计算公式如下：

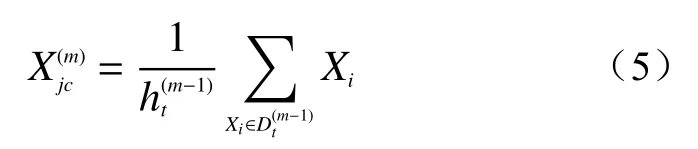
式中：m——迭代次数；

第m次迭代后属性指标j的聚类中心；

——第m−1次迭代后的分类结果（t=1,2,3,···,K）；

——第m−1次迭代后类别中的样本个数。

根据上述快速聚类原理分别对各定量影响因子聚类，每个定量因子聚类流程如图2所示，具体聚类流程如下：

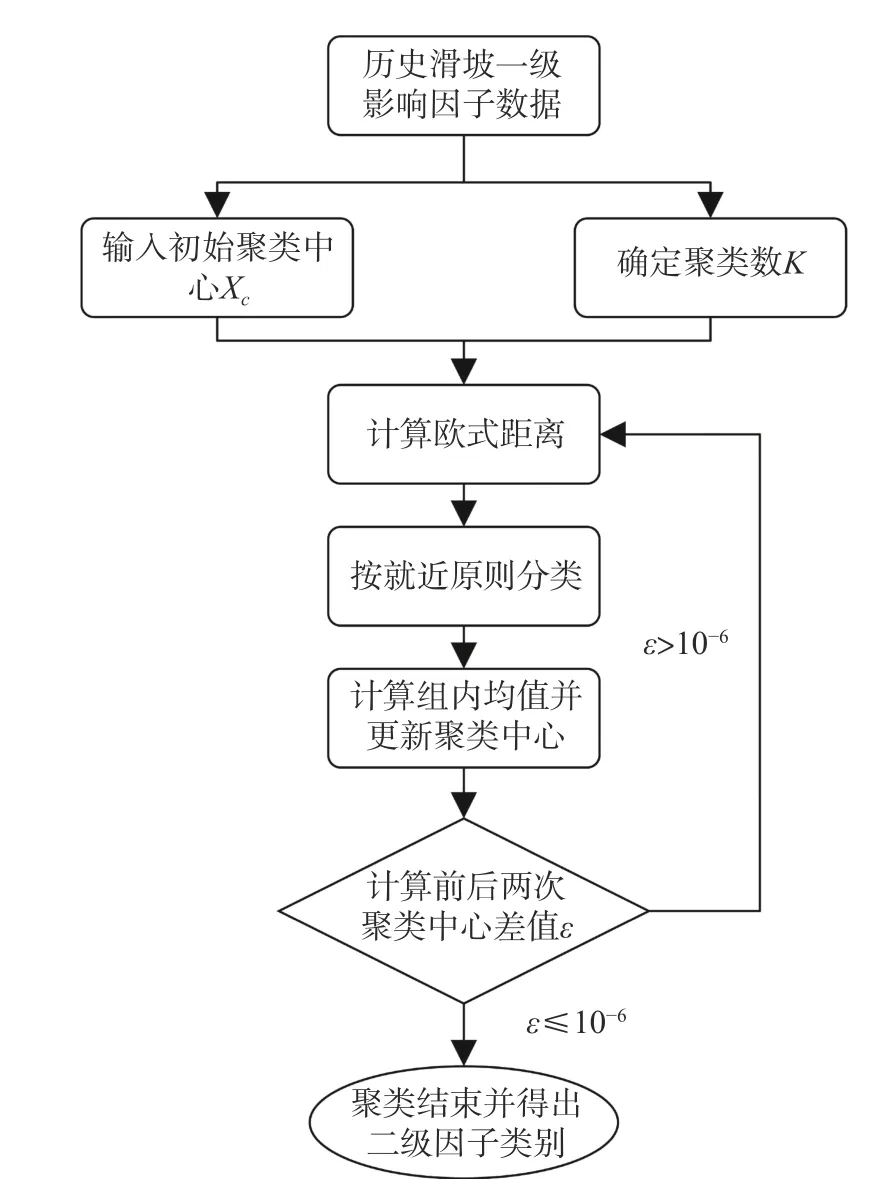
图2 快速聚类流程图Fig.2 Flow chart of K-means clustering model

（1）输入滑坡数据集单个定量影响因子属性值进行聚类分析（样本空间为一维）。

（2）输入初始聚类中心和所期望聚类数目K后，计算各样本距离初始聚类中心的欧式距离，并根据就近原则将各样本划分为K类。

（3）重新计算组内聚类中心（组内平均值），从而得到新一轮的聚类中心并重复上述过程直到前后两次聚类中心的差满足收敛条件。

（4）以各类别中影响因子属性值的最大值和最小值作为区间断点，从而确定各类别的划分区间，聚类结束。

2 研究区概况及数据源

2.1 研究区概况

选取相互毗邻的汶川县、理县及茂县作为研究区，三县位于四川省阿坝藏族羌族自治州东南部，总面积约为12 257.63 km2（图3）。地势由西北向东南倾斜，区内群山连绵，峰峦重叠，地貌为典型的高山峡谷区域，海拔762～5 974 m，高差悬殊，沟谷纵横。三县内三叠系、二叠系、侏罗系、志留系、石炭系、寒武系等地层均有出露，岩性复杂多变。研究区内主要分布有北东-南西走向斜穿汶川的茂县-汶川断裂和北川-映秀断裂，两侧有明显的片理和牵引构造的东西走向的石大关断层[13]以及马尔康北西向构造和薛城弧形构造。整体上地质构造复杂，新构造运动复杂，主要断裂带处岩体破碎，裂隙发育，风化严重，进一步导致滑坡发生。区内水系分布广泛，主要分布有杂谷脑河、土门河、寿江和草坡河等支流，最后由西向东汇入岷江。

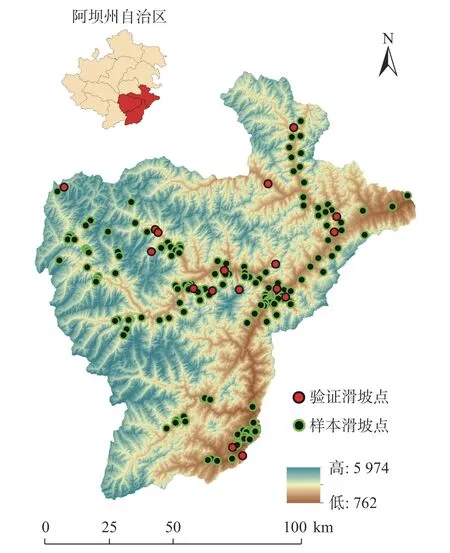
图3 研究区地理位置及滑坡调查图Fig.3 Location of study area and distribution of landslides

2.2 数据源

研究所采用的数据源主要包括：（1）滑坡分布数据共176处（其中分为训练样本159处与验证样本17处）来自于四川省自然资源厅和国家地球系统科学数据中心（国家科技基础条件平台—国家地球系统科学数据中心（http://www.geodata.cn））；（2）1∶50 000区域地质构造图；（3）30 m GDEMV2数字高程数据（地理空间数据云）；（4）研究区域水系矢量数据和地表覆盖数据均来自全国地理信息资源目录服务系统（www.webmap.cn）。

3 评价单元的选取与影响因子分级

3.1 评价单元的选取

滑坡易发性评价往往考虑多种要素的影响；为便于空间叠加等分析,常使用支持栅格数据结构的GIS软件或利用GIS栅格分析功能[17]，栅格数据存储形式有利于滑坡易发性评价的研究与计算。

进行栅格分析前，需统一栅格单元的大小，栅格大小对滑坡易发性评价的影响逐步传递。所以本研究根据研究区1∶50 000底图和李军等[17]提供的栅格大小选定经验公式计算：

GS=7.49+0.0006S−2.0×10−9S2+2.9×10−15S3（6）

式中：GS——栅格大小；

S——底图比例尺分母。

最终选定栅格大小为30 m×30 m，所以将研究区共划分为13 619 588个评价单元。

3.2 影响因子的选定

滑坡灾害发生是多个环境和人为因素共同造成，王磊[9]在理县地区以坡度、坡向、地层岩性、地质构造、河流水系、降雨、地震、人类工程活动为影响因子分析滑坡易发性；韩蓓[13]选取坡度、坡向、地层岩性、地质构造、河流水系、降雨和人类工程活动为影响因子分析岷江上游汶川-叠溪河段滑坡易发性；JIANG等[7]选取坡度、坡向、高程、岩性、地质构造、降雨、地震和土地利用类型作为汶川地区加权信息量模型的评价因子；王帅永[18]认为地震烈度、断裂带、水系、高程、坡度、岩性是汶川地区滑坡发生的主要因素；YANG等[19]选取坡度、地形粗糙度、高程、岩体、距公路的距离、地震烈度、距居民点的距离评价都汶公路滑坡易发性。

基于上述研究，并结合本研究区收集到的地质资料和矢量数据，选取坡度、坡向、高程、地层岩性、距构造的距离、距水系的距离以及土地利用为研究区滑坡灾害易发性评价影响因子[20−22]，最终结果见表1。

表1 影响因子选择Table 1 Selection of impact factors

3.3 影响因子的分级

影响因子的分级是指把每个影响因子按照一定分类标准分为对发生滑坡贡献相似的类别。本文为比较二级因子等距分类与快速聚类法分类对最终滑坡信息量结果的影响，对坡度、坡向、高程、距水系的距离、距构造的距离分别用上述两种方法进行二级因子的分类。地层岩性与土地利用则依据岩石坚硬程度和土地类型分类。

3.3.1 快速聚类法分类

本文根据159处滑坡样本点隶属的各因子值为样本进行快速聚类分析，将7个影响因子进行分类。

（1）坡度、坡向、高程

坡度、坡向和高程构成研究区3个的地形因子。本研究对坡度、坡向和高程因子分别借助SPSS软件进行快速聚类分析，分类结果如图4(a)、4(c)、4(e)所示。结果表明研究区滑坡主要集中于坡度在16°～37.1°内，其中16°～23.5°的滑坡比率较大；坡向在273°～360°范围内滑坡数与滑坡比率最大，各坡向区间面积比较均匀；高程在2 141～2 647 m滑坡发生较多，但在0～1 560 m范围内滑坡比率较大。

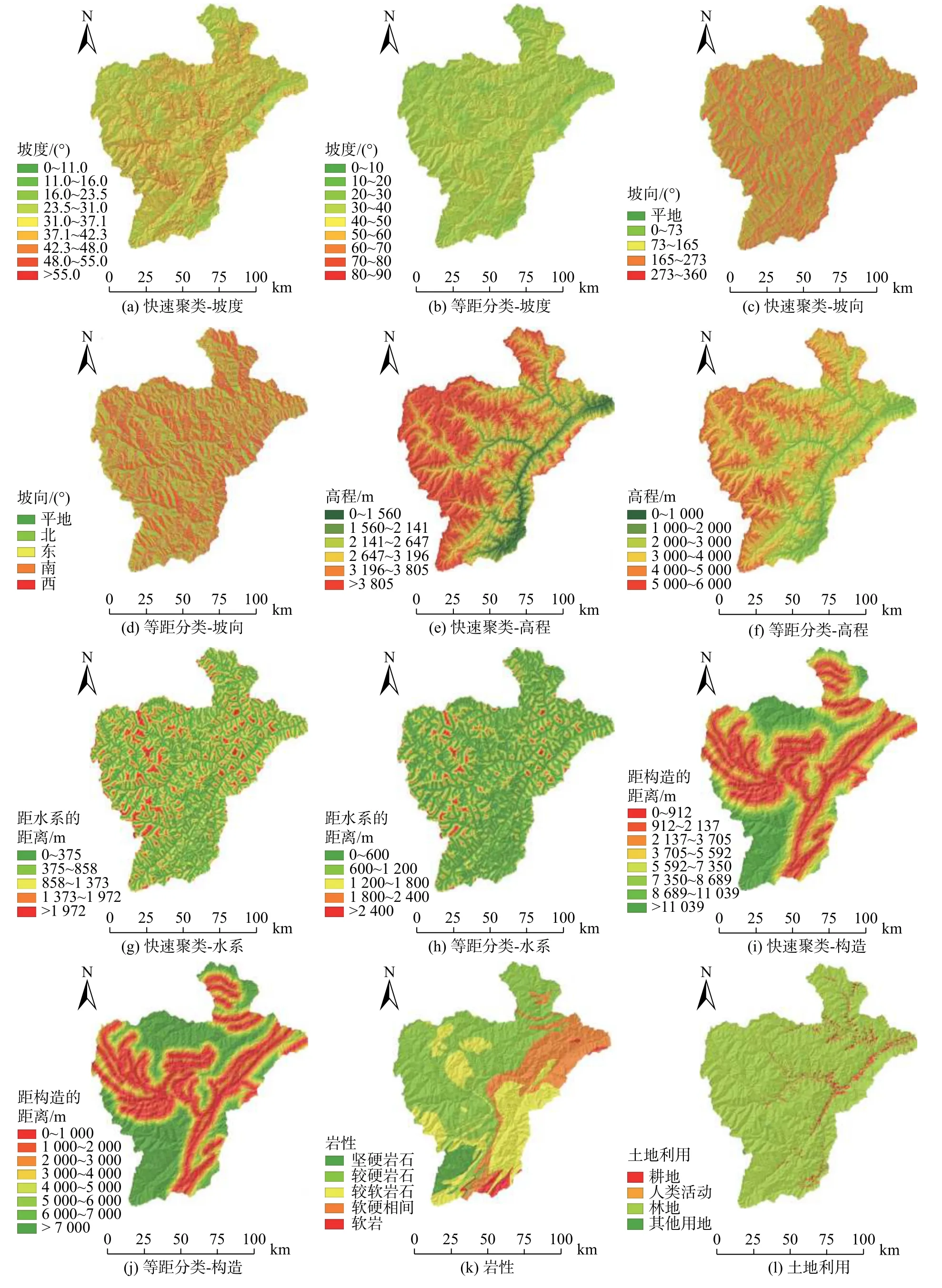
图4 影响因子分类图Fig.4 The classification diagram of the impact factors

（2）距水系的距离

研究区水系发达，河流密布，主要有岷江与其各大支流，水系的切割为滑坡的发生提供了临空面，滑坡分布与距水系的距离有着极其密切的联系[17]。本研究以159处滑坡点距水系的距离为样本，借助SPSS软件进行快速聚类分析，共将距水系的距离分为5类，分类结果如图4（g）所示。结果表明距水系0～375 m范围内滑坡比率最大，滑坡多发，随着距水系距离越远，滑坡数和滑坡比率逐渐减小。

（3）距构造的距离

地质构造是区域滑坡灾害分布的一大主导因素。本研究以159处滑坡点距构造的距离为样本，借助SPSS软件进行快速聚类分析，将该因子共分为8类，结果如图4（i）。结果表明距构造0～912 m范围内滑坡发生比率与频数均较大。随着距离构造越远，滑坡数和滑坡比率整体上呈现递减趋势，偶有波动。

（4）地层岩性

地层岩性是滑坡灾害发生的内在因素，由于研究区地层年代广泛，岩性复杂，分布有中分化-强风化岩浆岩、千枚岩、灰岩、泥岩、碳酸盐岩和砂岩等。本次根据岩石的坚硬程度将研究区岩石分为5类:①坚硬岩石；②较硬岩石；③较软岩石；④软硬相间岩石；⑤软岩。具体分类结果如图4（k）。

（5）土地利用

本文根据全国地理信息资源目录服务系统提供的地表覆盖数据将研究区土地类型分为4类：①耕地；②林地；③人类活动；④其他用地。具体分类结果如图4（l）。

3.3.2 等距分类法分类

为更直观地评价快速聚类法对二级因子分类的效果，亦同时开展了二级因子的等距分类，以便作平行对比。

（1）坡度、坡向、高程

本文对坡度以10°为间距分类；坡向则以地理方位分为东南西北与平地；高程以1 000 m为间距分类。分类结果如图4（b）、4（d）、4（f）所示。

（2）距水系的距离

水系以600 m为间距生成缓冲区，分为5类：0～600 m、600～1 200 m、1 200～1 800 m、1 800～2 400 m、>2 400 m。分类结果如图4（h）所示。

（3）距构造的距离

本文以1 000 m为间距，将距离构造的距离分为8 类：0～1 000 m、1 000～2 000 m、2 000～3 000 m、3 000～4 000 m、4 000～5 000 m、5 000～6 000 m、6 000～7 000 m、>7 000 m。具体分类结果如图4（j）所示。

（4）地层岩性与土地利用

地层岩性和土地利用则与3.3.1小节分类结果相同，分类结果如图4（k）、4（l）所示。

4 滑坡易发性区划分析

4.1 易发性区划原则

全区易发性区划依据研究区各栅格信息量的分布进行划分，区域信息量越高则其易发性越大。使用ArcGIS自然断点法将全区域滑坡易发性划分为5个等级：极高、较高、中等、较低、极低。ArcGIS自然断点法参考了聚类的思想，其认为样本之间存在着自然断点，能够将样本自然划分。依照这一思想，该方法通过寻找最大方差拟合优度（GFV）来确定最优划分类别，使得组内尽量相似，组间尽量相异，但是其与聚类方法不同的是该方法兼顾了各类别中样本数尽量相近，确保不存在特定类别样本数过少而引起的过度分类。

4.2 基于滑坡样本点数的区划分析

4.2.1 快速聚类-数量模型分析

首先，根据各影响因子快速聚类图层（图4）与滑坡样本点做空间分析，得到各因子各区间内滑坡数，并通过式(2)仅考虑滑坡数量计算各因子不同等级区间的信息量（表2）。之后对7个影响因子进行重分类，赋予各因子不同等级相应的信息量值。

最后利用ArcGIS栅格计算器对7个因子信息量值做栅格叠加运算，并用ArcGIS自然断点法将滑坡易发性信息量共划分为5个等级：极高、较高、中等、较低、极低。最终得到快速聚类-数量模型滑坡易发性区划图，如图5（a）所示。

4.2.2 等距分类-数量模型分析

依据4.2.1所述流程计算等距分类-数量模型，计算结果如表2所示，同样将信息量利用自然断点法分为5个等级：极高、较高、中等、较低、极低。分级结果如图5（b）所示。

4.3 基于滑坡样本面积的区划分析

4.3.1 快速聚类-面积模型分析

首先，将各因子快速聚类图层（图4）与滑坡样本点做空间分析，得到各因子各区间内滑坡总面积，并通过式（3）计算各因子不同等级区间的信息量（表3）。最后通过对各因子叠加分析和自然断点法将全区信息量分布同样分为5个等级：极高、较高、中等、较低、极低。分级结果如图5（c）所示。

4.3.2 等距分类-面积模型分析

与4.3.1所述流程相同，计算各因子不同等级区间的信息量（表3），最终得到等距分类-面积模型滑坡易发性区划图，并分为五个易发等级：极高、较高、中等、较低、极低。如图5（d）所示。

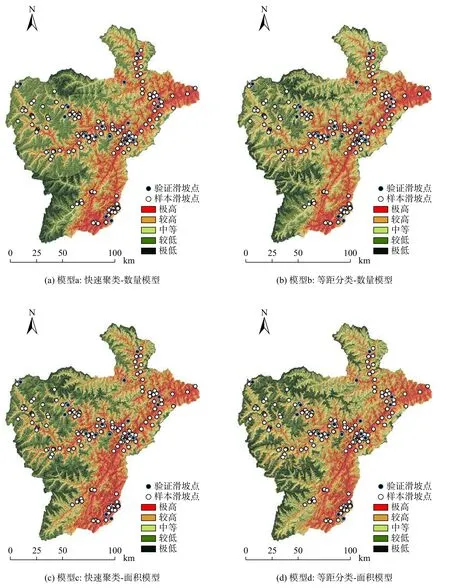
图5 研究区滑坡易发性区划Fig.5 Landslide susceptibility regionalization in the study area

4.4 影响因子信息量统计分析

为评价研究区各因子对发生滑坡事件的敏感性，根据表2和表3各二级因子信息量值，分别统计各影响因子信息量的均值和方差（图6）。关于影响因子信息量的统计分析有如下几点认识：

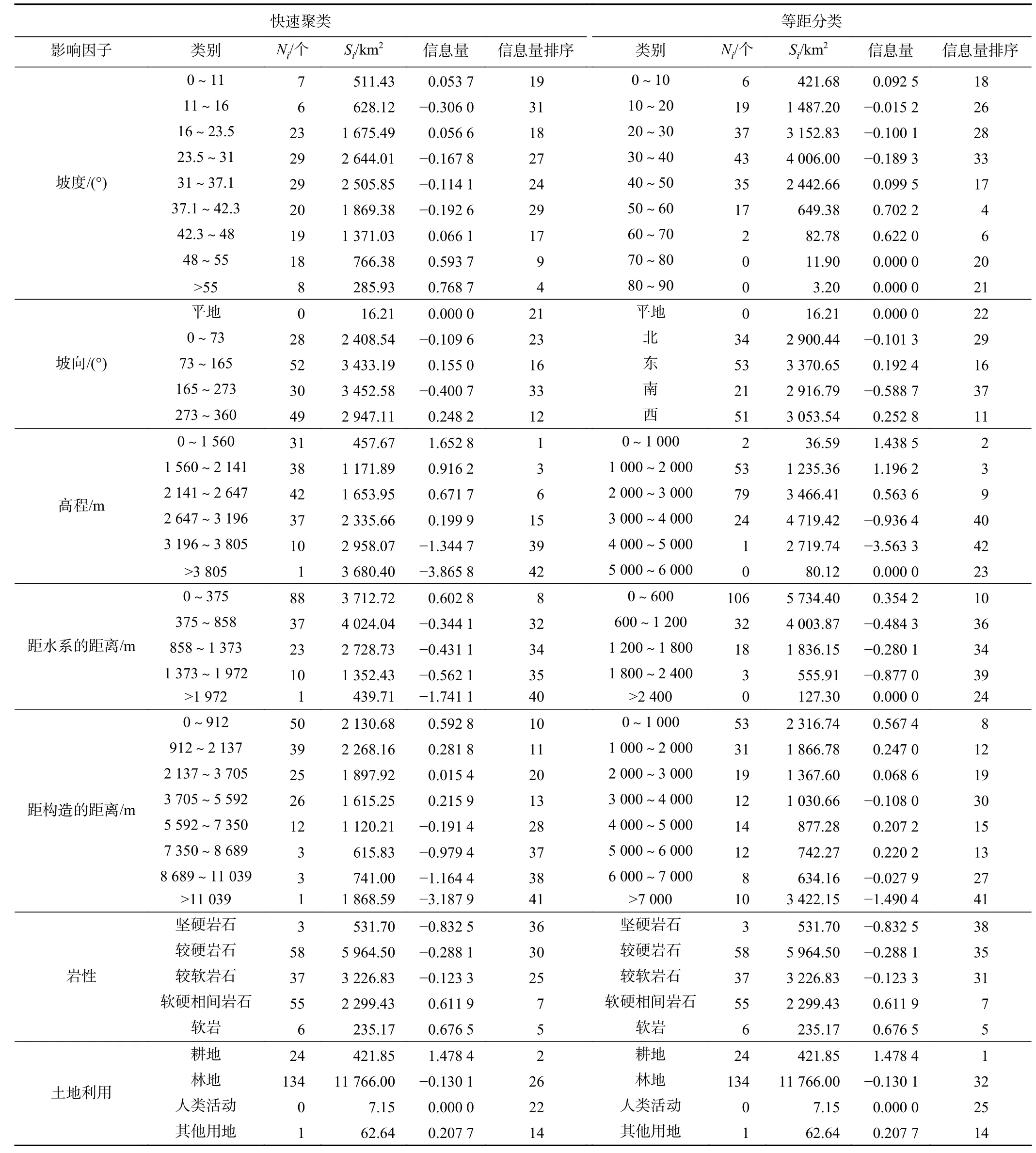
表2 基于滑坡样本点数的信息量表Table 2 Information table based on landslide sample points

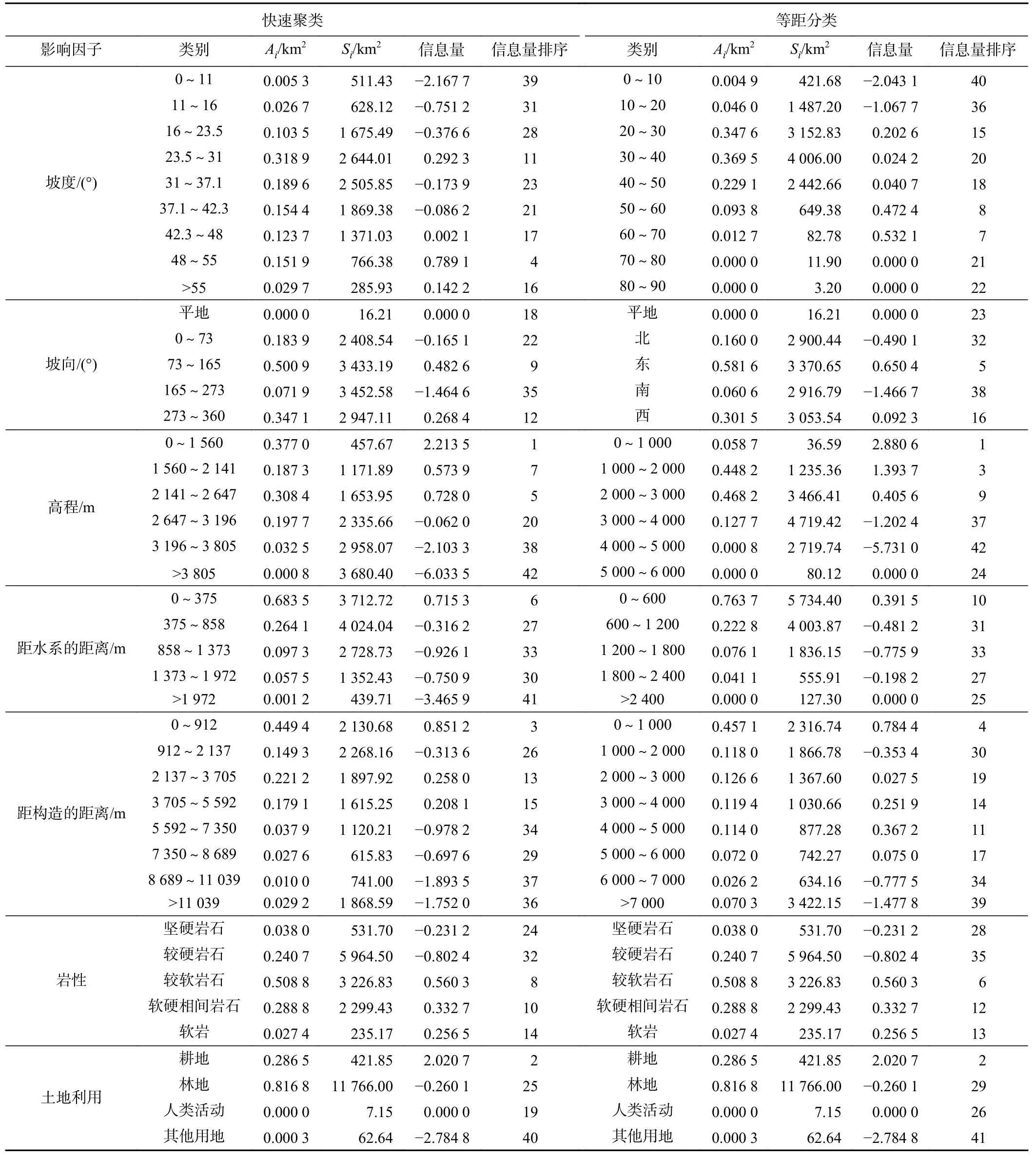
表3 基于滑坡样本面积的信息量表Table 3 Information table based on landslide sample area

第一，零信息量的含义。由式（2）和式（3）可知：二级因子信息量为零时表示滑坡发生条件下该二级因子出现的概率与该二级因子的面积占比（所覆盖的区域面积占研究区总面积的比例）相等。更进一步，如果某一级因子与滑坡发生与否不具有相关性，则其下的各二级因子所呈现的信息量将以零为数学期望。

第二，自然对数的非线性放大效应。信息量是取自然对数而得到，由于自然对数函数呈现出非线性的放大效应，且在自变量（0,1）区间内的函数值为负数，即自变量越小，函数值以指数倍方式取负值。由此当滑坡在各个档位的二级因子中分布不均匀时，某一档位的二级因子出现概率明显小于该二级因子的面积占比时，导致其信息量被放大为一个很大的负值，继而在求二级因子平均值时，很大程度上掩盖其它二级因子的信息量大小，从而整体上呈现出负数均值，如图6（a）所示。

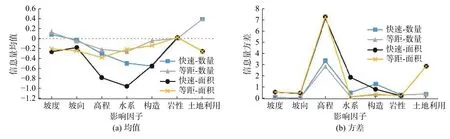
图6 影响因子信息量值统计分析图Fig.6 Statistical analysis diagram of impact factor information value

第三，信息量均值偏移基准线（零值）的程度，反映了该因子对滑坡发生的敏感程度。当某二级因子其下的若干分组对滑坡的敏感性有明显差异时，其信息量不但会呈现出较大的方差，如图6（b）所示，而且在上述第一、第二两条规律作用下，其均值将会明显偏移基准线。综上可知：偏移基线越远、方差越大，预示着该因子越敏感。

基于上述三点认识，从图6中可总结出研究区以下几点规律：

（1）同一影响因子在不同模型条件下，其均值偏离基线的程度不同，且方差也不相同。这反映了随着模型的逐步改进（由考虑仅滑坡数量改进为考虑滑坡规模、由二级因子等距分类改进为快速聚类），影响因子的敏感性被逐步挖掘出来。模型c相比较其他模型而言，离基线更远，且方差更大，预示着有最好的数据挖掘潜能，对滑坡的识别更加敏感；与之相反，模型b的数据挖掘潜能最低。

（2）在模型c条件下：从图6（a）可知，高程、水系、构造这三个因子被凸显；而从图6（b）来看，则是高程、水系、土地利用这三个因子被凸显。综上可知，高程和水系这两个因子对判断滑坡易发性最为敏感。

（3）由于岩性和土地利用的二级因子是通过定性分类，故其信息量值存在重合点，无法体现快速聚类的优势。特别是岩性因子，其信息量均值接近基准值，且方差低，表明该因子对指示滑坡发生与否相对不敏感。

4.5 滑坡区划结果分析

由图5可知四种区划方法存在差异，但其中都能发现：

（1）极高易发区与较高易发区主要分布于水系干流与各大支流附近，例如岷江，杂谷脑河等，其信息量排名在表2和表3中均在前10名。

（2）龙门山断裂带、理县薛城弧形构造以及马尔康北西构造地区滑坡易发性高，这可能是由于构造运动活跃，断裂带致使岩体破碎，裂隙发育，例如汶川东部多分布中风化至强风化的岩浆岩，其信息量排名较高。

（3）极高易发区多分布于2 000 m高程以下范围，且极高易发性地区大多分布有较软岩石、软硬相间岩石与软岩且多见于耕地，这可能是因为人为改造边坡的植被覆盖与地形导致滑坡多发，表2和表3中耕地信息量排名均在前2也能证明耕地对滑坡的影响。

4.6 精度评价

4.6.1 基于高危区占比的精度评价

为分析研究区滑坡易发性评价结果的准确性，并对两种分类方法以及计算时是否考虑滑坡面积进行比较，故对四种模型分别进行横向与纵向的分析对比。本研究利用从176处滑坡点中随机抽取的17处验证滑坡点和159处样本点对上述四种方法评价结果进行验证，同时根据滑坡易发性区划图（图5）统计各易发区滑坡发生占比与滑坡比率，结果如图7和图8所示。由图7（a）所示，将各模型极高易发区与较高易发区的滑坡占比相加发现：①模型a（快速聚类-数量）的样本点中分布于极高和较高易发区的滑坡占比总和为93.08%，高于模型b（等距分类-数量）的对应值86.16%；②模型c（快速聚类-面积）中样本点在极高和较高易发区的滑坡占比总和96.27%，也高于模型d（等距分类-面积）中对应值93.81%；③模型c（快速聚类-面积）中样本点在极高和较高易发区的滑坡占比总和为96.27%，高于模型a（快速聚类-数量）的对应值93.08%；④模型d（等距分类-面积）中样本点在极高和较高易发区的滑坡占比总和为93.81%也明显分别高于模型b（等距分类-数量）中对应值86.16%。与图7（a）类似，由图7（b）展示的验证点统计规律也符合上述①～④条。

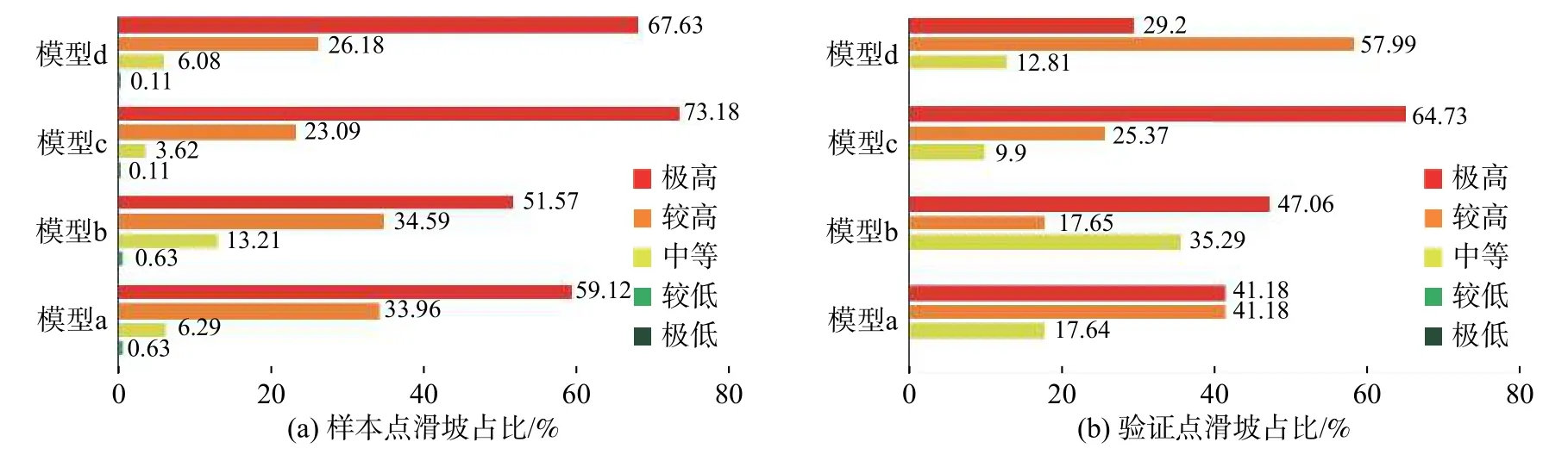
图7 四种模型评价结果对比之:滑坡占比(易发区间滑坡/总滑坡)Fig.7 Comparison of the evaluation results of the four models: landslide proportion (susceptibility grade landslide/total landslide)

综合①②说明快速聚类法优于等距分类；综合③④说明考虑滑坡面积的模型具有优势，而常规的仅考虑滑坡数量的方法，由于忽视了滑坡规模对信息量的影响，存在弊端。

由图8可以得出模型a（快速聚类-数量）与模型c（快速聚类-面积）验证点与样本点在不同易发性区间的滑坡比率分布趋势较为一致，即随着滑坡易发性等级的增加，各级滑坡比率逐渐递增，符合滑坡易发性等级划分原则，但是模型b（等距分类-数量）和模型d（等距分类-面积）中验证点在不同易发性区间的滑坡比率分布趋势不一致，出现较高易发区的滑坡比率小于中等易发区（模型b）和极高易发区滑坡比率小于较高易发区（模型d）。上述规律也可以佐证快速聚类法优于等距分类法。

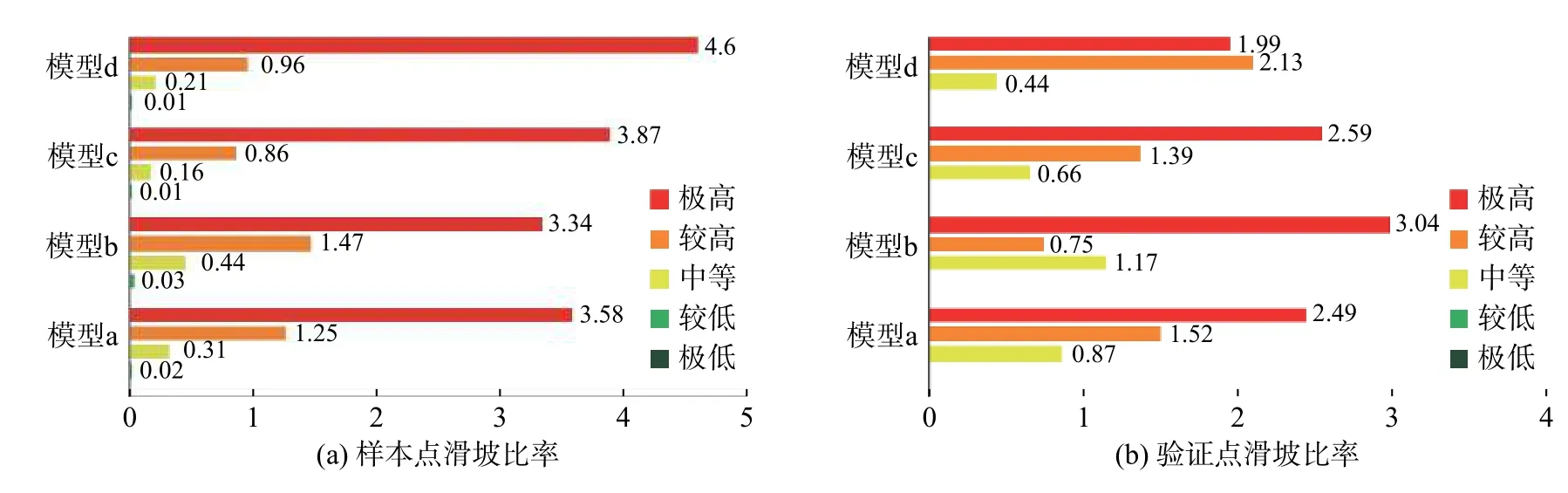
图8 四种模型评价结果对比：滑坡比率（滑坡占比/易发区间面积比）Fig.8 Comparison of evaluation results of the four models: landslide ratio (landslide proportion/area ratio of susceptibility area)

4.6.2 基于AUC的精度评价

为进一步评价两种分类方法以及信息量计算时是否考虑滑坡面积对于信息量模型预测精度的影响，故以滑坡易发面积百分比与其对应的实际滑坡累加占比构建成功预测曲线，结果如图9所示。图9表示易发性逐渐递减的情况下实际滑坡发生累积百分比的变化情况，曲线越靠近左上角，曲线下面积（AUC）越大则表示模型评价精度越高。由图9可知模型a线下面积比（AUC）为81.95%，模型b为80.46%，前者比后者高出了1.49%，评价精度有所提升。其次，在同时考虑滑坡面积时，模型c优于模型d，精度提升1.62%，上述亦可证明快速聚类法优于等距分类法。在相同二级因子分类方法下，模型c比模型a精度提升了5.30%；模型d比模型b精度提升了5.17%，说明考虑滑坡面积信息量计算更为精确。最终在快速聚类法和考虑滑坡面积信息量计算的两项优势加持下可以得出快速聚类-面积模型（模型c）为最优评价模型（AUC=87.25%），结合图7和图8的精度评价结果证明二级因子快速聚类法与考虑滑坡面积的信息量计算法能够提升滑坡易发区域预测精度，对研究区滑坡地质灾害预测与防治具有实际意义。

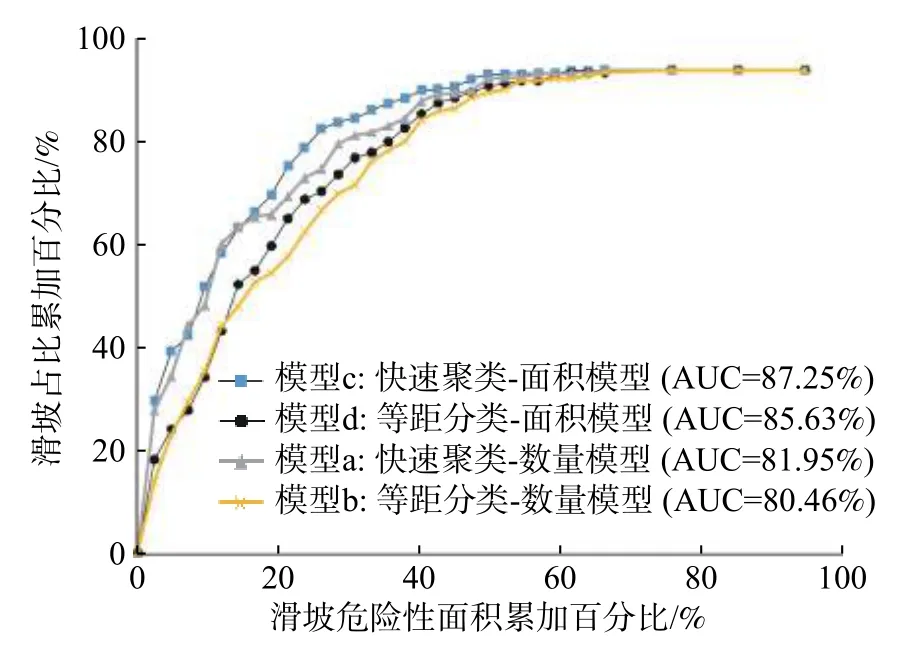
图9 滑坡成功预测曲线Fig.9 The curve of successful landslide prediction

5 结论

本文提出了基于快速聚类法的信息量模型，并以汶川及周边两县（理县和茂县）为例，开展了滑坡灾害易发性评价。主要结论如下：

（1）将汶川及周边两县（理县和茂县）滑坡灾害易发性分为极低、较低、中等、较高、极高五类。其中较高和极高易发区主要集中于高程较低的主要水系或断裂带附近，岩性通常在较软岩石以下，且多见于耕地。评价结果对该区域滑坡地质灾害的防控提供了参考。

（2）新模型采用快速聚类法对二级因子的分类进行了优化，提高了滑坡易发性评价的精度。与传统的等距分类法评价结果对比表明：①快速聚类-信息量模型的AUC值高于等距分类-信息量模型；②验证点与样本点不仅滑坡比率的分布更为符合滑坡易发性等级划分的基本原则，而且处于极高易发区与较高易发区的滑坡占比均高于等距分类法。因此，基于快速聚类-信息量模型比等距分类-信息量模型在滑坡灾害易发性预测方面有着更高的精度。

（3）通过对计算信息量时是否考虑滑坡面积，将上述新模型继续分为两个子类。比较发现，在相同二级因子分类方法的前提下，考虑滑坡面积的信息量模型均优于基于滑坡数量的信息量模型，其AUC值分别提高了5.30%（模型c比模型a）和5.17%（模型d比模型b）。