融入课程思政元素的导数定义教学设计

刘 薇，常振海，高忠社

2020年5月《高等学校课程思政建设指导纲要》（以下简称《纲要》）中指出：公共基础课程要注重在潜移默化中坚定学生理想信念、厚植爱国主义情怀、加强品德修养、增长知识见识、培养奋斗精神，提升学生综合素质；要以课程为基本载体，梳理课程教学内容，深入挖掘课程中的思政元素，将之有机地融入课程的教学过程中［1］.不同学科的学者们已经进行了有效的探索［2−7］.

“高等数学”是大学诸多专业的公共基础课程，依据纲要的精神，如何在“高等数学”的课堂上开展好思政教学成为了每一名高校数学教师义不容辞的责任和义务，已经有许多学者将高校思想政治教育工作融入大学数学课程教学［8−12］，把改革的各环节、各方面贯穿于教育教学全过程，实现知识传授、能力培养与价值引领的有机统一，使专业教育与思政课程协调同步、相得益彰，真正实现在课堂教学主渠道中全员、全方位、全过程立体化育人.

通过“高等数学”课程的教学，要使学生掌握处理数学问题的思想和方法，逐步培养学生比较熟练的基本运算能力和自学能力、综合运用所学知识去分析和解决问题的能力、初步抽象概括问题的能力以及一定的逻辑推理能力.而导数的定义又是“高等数学”教学中一个十分重要的内容，它在整个课程体系中起着举足轻重的作用，它是微分理论的核心，也是后续学习积分理论的基础.本文针对“高等数学”中导数的定义这节教学内容，科学设计了课程思政的教学体系，将德育元素融入到教学中.通过我国高铁运行视频中的两个具体问题，提出要解决的瞬时速度和切线的斜率问题，通过讲述中国高铁辉煌成就激发学生的爱国情怀，同时在解决问题时引导学生用全面、发展、联系的观点看问题，无论是学习还是生活中可能每个人都会遇到许多意想不到的问题，我们在处理时都要用运动、变化、发展的观点看问题，不能用僵化的、静止的、不变的思维来思考问题，教学中渗透了辩证唯物主义的观点.解决了相关问题后，又通过相关研究的历史背景以及科学家的介绍，鼓励学生学习科学家身上那种孜孜不倦、勤奋探索的科研精神，培养学生严谨客观的科学态度，增强了课程的知识性、人文性、引领性和时代性.

1 教学设计思路

依照“教学理论”和“学习理论”对教学内容进行了设计.“教学理论”能保障在教学设计时进行通盘考虑，让教学设计符合教学上的普遍规律，让设计者能站在更高的角度对教学任务、教学方法、教学手段、思政教育以及教学评价等进行合理的设计.“学习理论”能让学生在刺激（如高铁视频）和反映（如发现的两个问题）之间建立联系，有利于学生通过情景对问题进行认知、顿悟和理解，有利于学生对知识进行再构造，从而将知识转化为学生解决问题的能力.

1.1 教学方法：问题驱动、诱导探思教学法、类比和归纳

在教学中，主体是学生，主导是教师，主线是知识，主旨是发展思维，纽带是问题，给学生创设相关的问题情境，通过适当的引导，使学生通过类比归纳得到导数的概念，引导学生体验数学相关知识再发现的过程，知识的获取、思维的发展以及数学的感悟都在学生的参与中得到体现，这样就自然地实现了本节课的教学目标：掌握知识，发展能力，陶冶品德.

1.2 教学手段：多媒体、慕课堂辅助教学

通过PPT演示和慕课辅助能够弥补传统教学的不足，使得难以理解的教学概念更加直观，使得学生能够更好地理解无限逼近的极限思想，从而使得学生能够较好地理解导数的本质.通过中国高铁视频展示讲解，增强学生的爱国情怀，激发学生的科学探索精神.通过相关背景知识介绍调动学生的学习兴趣.通过多媒体、慕课及黑板演示等方式来突破本节课的重点和难点.

1.3 思政教育：通过例子引出问题，体现思政与教学内容的有机结合

首先，以我国高铁的一段视频为例，提出两个问题：如何求变速直线运动的瞬时速度和求曲线的切线斜率.启发学生通过探究得到这两个问题的答案.通过中国高铁激发学生的爱国情怀，通过问题的探究培养学生分析解决问题的能力和辩证唯物主义思想.接下来对所讨论的这两个问题，给出它们研究的历史背景，早在17世纪的时候它们就由英国的数学家牛顿和德国的数学家莱布尼茨进行了研究，由这两个问题以及解决相关问题而发展起来的数学理论称为微分学，这是“高等数学”研究的主要内容.由引例的结论归纳总结得到导数的定义，再回顾两个引例得到导数的物理意义和几何意义.最后给出了利用导数判断函数可导以及利用定义计算导数的方法.

本教学设计的思维导图如图1所示.

图1 思维导图

2 教学过程

2.1 问题的提出

首先创设情境，以案例式教学方式给出现实生活中的一个实际问题：我国高铁运行的一个简短视频.视频中高铁的车厢内显示了高铁每个时刻的运行速度，同时也会显示高铁在弯道内平稳的运行，示意图如图2所示.

图2 列车瞬时速度和弯道平稳性实验（乘客）

接下来给学生介绍我国铁路发展的历程，一代代的铁路人经过了不懈的努力才取得了今天高铁辉煌的成就.中国如今拥有世界上首条新建的高寒高铁，世界上单条运营里程最长的高铁，世界上一次性建成里程最长的高铁，截至2020年底，中国高速铁路运营总里程达3.8万公里，居世界第一.列车最高运营速度350千米/小时，居全球首位.高铁已经成为中国科技创新的标志性成果，也是中国向世界递出的一张靓丽的名片.在视频中同学们看到了飞驰的高铁，一定会为我们伟大的祖国感到骄傲和自豪.通过例子激发学生的爱国情怀，同时也可以增强学生的责任感和使命感.

同时提出两个问题：第1个就是高铁在运行的时候，电子屏幕上时刻会显示它的运行速度，每个时刻的速度都是不同的，这个速度是如何求出来的?第2个就是高铁在驶入弯道的时候，为了保持高铁的平稳运行，设计轨道时会涉及到求曲线的切线斜率问题，那么曲线的切线斜率又该怎么求解的呢?

2.2 问题的解决

（1）变速直线运动的瞬时速度问题.把高铁看作质点（如图3中直线上实心圆点），设质点做变速直线运动，其位移函数为S=S(t)，怎样求t0时刻的瞬时速度呢?

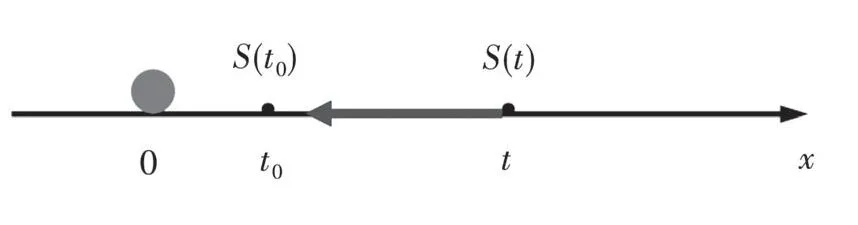
图3 高铁直线运动抽象化

为了求出t0时刻的瞬时速度，再取一个时刻t，先计算出从t0到t时间间隔内的平均速度，平均速度就等于这段时间内所经过的路程除以所需的时间，即当所取的时间间隔很小时，从t0到t时间间隔内的平均速度就很接近时刻t0的瞬时速度，可以用平均速度近似代替t0时刻的瞬时速度.若所取的时间间隔越小，则这个平均速度就越接近t0时的瞬时速度.让t无限地趋近t0，若平均速度的极限存在，这个极限值就是质点在t0时刻的瞬时速度.

（2）曲线上一点处的切线斜率问题.设曲线C为函数y=f(x)的图像（图4），列车在弯道的运行可看作是曲线上点M沿着曲线运动，列车在弯道处的运动方向可看作是求切线MT的斜率.

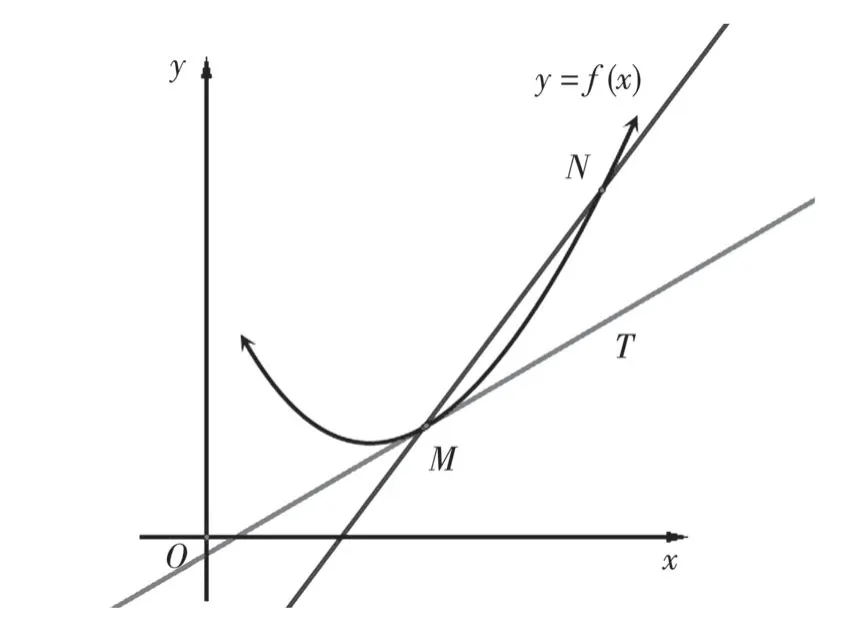
图4 列车弯道平稳性实验抽象化

为求切线MT的斜率，记曲线C上点M(x0,f(x0))，在曲线C上再取一点N(x,f(x))，作割线MN，其斜率为

当点N沿曲线C无限接近于点M.割线MN的极限位置就是曲线C在点M处的切线.当点N沿曲线C无限接近于点M时，则有x→x0，对割线MN的斜率取极限，若极限存在，则该极限值就是切线MT的斜率.

从上面的两个例子我们可以看到，当间隔取得足够小，平均速度的极限就是瞬时速度，割线斜率的极限就是切线斜率.世界上没有僵化的一成不变的事物，整个世界是一个变化发展的世界，我们对待问题的看法，处理问题的方法也应该是变化的、发展的，生活中的喜怒哀乐都是暂时的，只要你能正确的面对，科学的处理，一切都会向着好的方向发展.

2.3 问题的历史背景

其实讨论的这两个问题，早在17世纪，就由英国的数学家牛顿和德国的数学家莱布尼茨进行了研究.由这两个问题以及解决相关问题而发展起来的数学理论称为微分学.接着为同学们介绍两位伟大的数学家牛顿和莱布尼茨.

17世纪下半叶，英国的数学家牛顿为解决运动问题，创立了这种和物理概念直接联系的数学理论，牛顿称之为“流数术”，实际上就是微积分理论.牛顿用它处理了一些具体的问题，如求积问题、瞬时速度问题以及函数的极大值和极小值问题等.同时德国的数学家莱布尼茨是经过研究曲线的切线和曲线包围的面积，运用分析学方法引进了微积分的概念，得出了相应的运算法则，从几何方面发现了微积分.莱布尼茨创立微积分的途径和方法与牛顿是不同的，牛顿在微积分的应用上更多的结合了运动学，造诣较莱布尼茨高一等，但莱布尼茨创造的微积分符号却又远远优于牛顿，既简洁又准确地揭示了微积分的实质，强有力的促进了微积分的发展.因此，牛顿和莱布尼茨被公认为是微积分的创立者和奠基人.

通过介绍激发学生的学习兴趣，让学生了解数学发生、发展的相关历史，培养学生刻苦钻研及勇攀科学高峰的责任感和使命感，同时也提高了学生的人文素养.

2.4 导数的定义

抛开这两个例子的具体意义，抓住这两个问题的共性，就可以得到导数的概念.设函数y=f(x)在点x0的某个邻域内有定义，若

极限存在，则称函数y=f(x)在点x0处可导，并称此极限为函数y=f(x)在点x0处的导数，记作或f′(x0).

在引例1中，瞬时速度所得结果就可写为s′(t0)，其物理意义为质点在t0时刻的瞬时速度.在引例2中，切线的斜率所得结果就可写为f′(x0)，其几何意义为曲线y=f(x)在点(x0,f(x0))处切线的斜率.

根据导数的定义

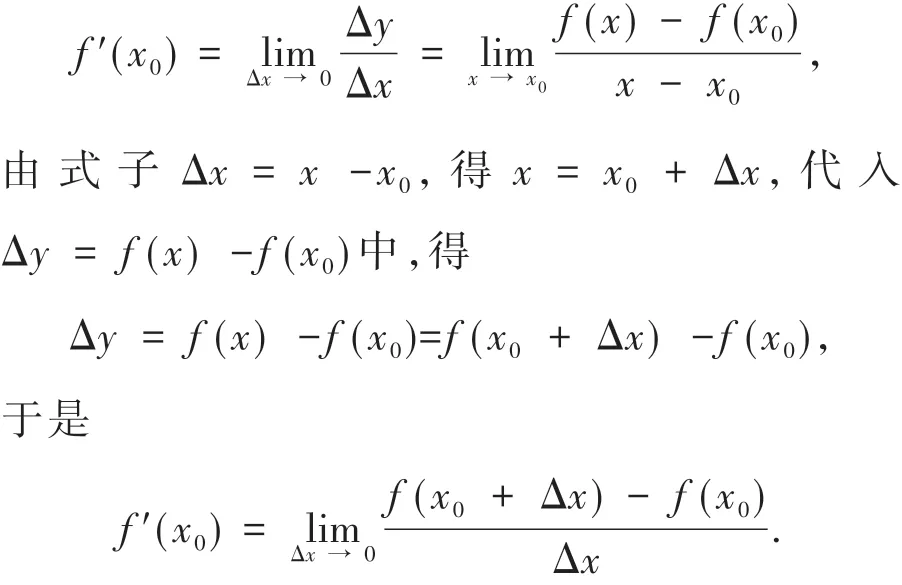
如何判断函数在一点是否可导呢？通过求差商的极限，若极限存在则函数可导，若极限不存在则函数不可导.因此，导数的定义式既可用于判定又可用于计算.

例 求函数f(x)=x3在点x=1处的导数.

板书解题过程，并引导学生总结归纳求函数在一点处导数的步骤.

2.5 学习小结

通过视频，本节课引出了两个问题，通过探索由平均速度得到瞬时速度，由割线斜率得到切线斜率，从而使得两个问题得到了解决，并且归纳抽象出了导数的概念，得到了导数的物理意义和几何意义.最后利用导数定义给出了判断函数可导以及计算导数的方法.

3 结语

本文是深度挖掘课程思政教育功能的具体案例，结合导数定义在课堂三个恰当的节点处不着痕迹地引入思政元素.第一处是中国高铁行驶的视频，引入该例子达到两个目的：一是引出我国现阶段的靓丽名片——中国高铁，潜移默化地激发学生的爱国情怀；二是引出和导数概念相关的两个问题，有力地帮助学生了解导数的实际背景以及几何意义和物理意义.第二处是在解决相关问题时运用了运动、变化、发展的唯物主义观点，平均速度取极限得到瞬时速度，割线斜率取极限得到切线斜率，引导学生用发展的观点看问题，坚持与时俱进，培养学生的创新精神.第三处是微积分发展的相关历史以及科学家的介绍，目的是培养学生刻苦钻研和勤奋向上的科研精神和学习态度.从而在知识学习上、思想方法上以及情感教育上达到有机的融合，达到课程初始设计的目的，特别是引入课程思政的目的.