分数Brown运动驱动的Levy-Heston模型下金融理财产品定价问题研究
董 艳
(陕西铁路工程职业技术学院,陕西 渭南 714000)
一、目的意义
1.研究目的
金融衍生产品定价是金融数学的重要内容之一,也是近年来人们在金融数学领域研究的一个重要课题。此外本课题的研究也具备一定的实践意义,本课题所得结果方便投资者和金融机构量化各种金融衍生产品的价值,对金融市场上的投资活动具有指导意义。
此外在生活中,期权也有诸多应用,期权与人们的日常生活息息相关。虽然“期权”二字没能出现在每个人的生活当中,但是期权的观念早已深入人心。除了上面论述的理财产品和定期存款问题以外,按揭买房和抵押贷款问题也可以通过期权找到合理解释[1-2]。
2.研究意义
近年来,金融理财产品得到了长足发展,针对人们不同的风险偏好和投资回报期望,一些金融机构推出一系列金融理财产品以满足人们投资理财的需要,见表1。
表1罗列了农业银行公布的诸多理财产品,总计6500多项,受篇幅的限制,这里只列出其中比较有代表性的8项。理财产品大概分为以下三类:非保本浮动收益型、保本浮动收益型和保本固定收益型。保本固定收益型理财产品,其收益率是固定不变的,投资者按照实现约定好的利率、投资期限和本金金额进行投资,到期之后领取约定的本金和利息。保本浮动收益型理财产品在国内外风行多年,不论市场走空还是走多,其本金是可以保证的,不会因为市场的变动影响生活,但是其收益是得不到保证的,其收益率往往随着金融市场发生变动。相比之下,非保本浮动收益型理财产品的本金和利息完全暴露在风险之下,其本金和利息都不是固定的(非保本浮动收益型理财产品的期望收益率高),可能要面临一定的本金亏损。
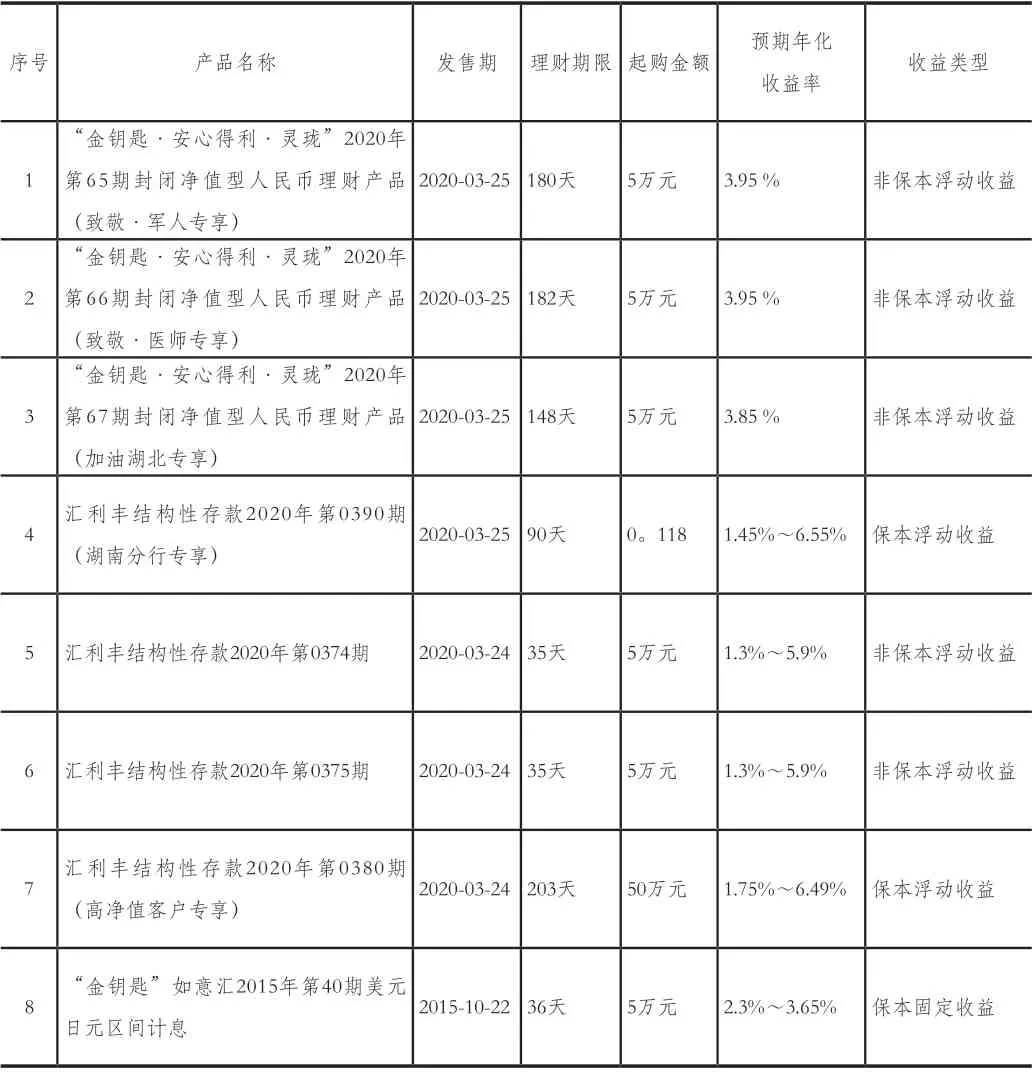
表1 农业银行部分理财产品
(1)理财产品中欧式期权的嵌入
对比保本浮动收益型理财产品和非保本浮动收益型理财产品:①对于保本浮动收益型理财产品,理财产品公司承诺本金的同时,还事先约定一个最低的收益率,这样一来,投资人在到期日T 是可以保证本金和最低的收益的,同时还可以保留因理财产品溢价而带来的意外获利的机会;②对于非保本浮动收益型理财产品,其本金和利息都是有风险的,其价值由市场决定。
因此,保本浮动收益型理财产品相当于在非保本浮动收益型理财产品的基础之上嵌入了一个欧式期权。对于这两种理财产品如果到期日相同,那么其单位本金的利息之差就应当恰好是一个欧式期权。
本文具体分析嵌入期权的种类。一方面,由于理财产品只有到期之后才可以获得利息和本金,从而理财产品中嵌入的期权只能是欧式类型。另一方面,大部分理财产品只与到期日的风险资产价格有关,与风险资产在理财产品合同续存期内的价格无关,那么此类理财产品中嵌入应当是标准欧式期权;有些理财产品(例如表1第一项和第二项)则规定了观察日,使得理财产品的收益依赖观察日风险资产的价格,那么此类理财产品中嵌入应当是欧式重置期权;最后还有一些理财产品(例如表1中第八项)其收益还依赖风险资产的价格在某个区间停留的天数,此类理财产品中嵌入应当是欧式阶梯期权。
(2)金融理财产品中美式期权的嵌入
这三种类型理财产品还有一个共同的特征:在投资期限内,拥有100%的资金使用权,通常不允许投资人提前支取理财产品,即便允许,也面临着高额的提前支取费用。相比之下,银行存款就便利许多,储户在以定期存款的形式将本金存入银行之后,如因为个人原因急需使用该本金时可以提前支取,但是提前支取的钱款按支取当日的活息利率计息。因此,定期存款相当于在理财产品的基础之上嵌入了一个美式期权。
(3)国内外研究现状及分析
由于定期存款和理财产品中所嵌入的期权分别为欧式期权和美式期权,本节对这两种期权的研究进展以及发展现状做一个简要的说明。期权定价问题的研究始于 20 世纪 70 年代初。首先研究的是几何布朗运动情形下的期权定价。Panini和Srivastav使用Mellin变换将期权适合的抛物方程转化为常微分方程并求解,然后利用Mellin逆变换给出了欧式期权的定价公式并给出了美式期权价格适合的积分方程。由于Mellin变换仅仅在波动率和利率为常数时候才可以进行,Frontczak和Schöbel在Panini和Srivastav结论的基础之上,考虑有连续红利支付情形下的欧式期权定价问题。通过 Mellin变换方法,得到了相应的欧式期权和美式期权定价结论。Company等人则对Panini和Srivastav的结论做了另一种推广,假定期权在到期日的收益是原生资产价格的一般函数,甚至允许收益函数包含有限个第一类间断点,利用傅里叶变换方法得到了欧式期权定价公式。Chanane用变量分离方法代替Mellin变换方法研究了欧式期权定价问题。Chanane提供的方法允许收益函数存在有限个间断点(第一类和第二类间断点均可),得到了更为一般情形下的期权定价结论。由于美式期权没有解析定价结论,除了采用数值方法(有限差分、有限元,Monte-Carlo)以外,易法槐老师及其研究团队采用惩罚方法研究了美式期权定价的自由边界问题,给出了美式期权弱解的存在性和唯一性,并研究了自由边界的光滑性。
分数布朗运动或者混合分数布朗运动驱动的Black-Scholes模型下的期权定价问题研究相对较晚。有学者研究了时变分数布朗运动驱动的B-S模型下的欧式期权定价问题,他们提供了一种新的随机微分展开方法用以代替Ito公式,据此给出了欧式期权满足的偏微分方程及其精确解的表达式。Chen.W研究了混合分数布朗运动情形下的美式期权定价问题。第一种是利用迎风差分格式研究了美式期权满足的变分不等式,给出了美式期权定价的数值算法。由于混合分数布朗运动情形下的美式期权变分不等式是分数阶的,第二种采用Liouville导数定义了变分不等式的弱解,并采用惩罚方法证明了该弱解的存在性。同时第二种还给出了美式期权价格的若干估计。
Levy模型适合用于模拟那些突发事件引起的风险资产价格变动。因此期权定价之Levy模型的提出受到了众多学者的欢迎。很多学者研究了Levy模型下的欧式期权定价问题,都将欧式期权转化成了一种Integro-differential型抛物偏微分方程。由于Integro-differential型抛物偏微分方程是非线性的,没有解析解,M.C.Mariania、M.Fakharany等采用数值方法研究了Levy模型下的欧式期权和美式期权定价问题。M.C.Mariania采用有限差分方法,得到了欧式和美式期权的一个二阶差分格式。此外,他还重点研究了差分格式的误差估计问题。M.Fakharany采用鞅方法研究了美式期权定价问题,得到了美式期权价格的一个半解析近似公式。
近些年来,CEV模型已经成功地应用于期权定价问题。J.Lee采用鞅方法研究了CEV模型下的欧式期权定价问题,采用无穷多个Bessel函数的线性组合表示出了欧式期权的价格公式,实际上其结果是半解析的。文献J.Lee也间接表明,由于CEV模型下的B-S方程不是常系数的,期权定价问题是不可能有精确解析解的。F.Kleinert利用有限差分方法研究了美式看跌期权的价格,Y.L.Hsu则研究了美式期权自由边界的位置。
随机波动模型也是学者研究的一个重要方向。随机波动模型克服了传统Black-Scholes模型中波动率为常数的假设。在金融实践中波动率常常呈现一定的随机因素,随机波动模型正好解决了这一问题。R.Griego通过数据统计分析,给出了某些风险资产的波动率遵循的特定分布,并在此基础之上研究了随机波动率下的期权定价问题。文献引入了各种形式的随机微分方程刻画波动率,形成了一系列的随机波动方程,也研究了期权定价问题。Heston模型用CIR方程来刻画随机波动率,预示着波动率在一定的水平上进行随机扰动,当波动率偏离平均水平后很快会恢复。S.Fallah研究了双随机项下Heston模型解的存在性和收敛性,A.Aghda则研究了延迟Heston模型解的收敛性,并且构造了一种Euler网格划分方法,在此差分格式下研究了解的非负性。E.Berthe在Heston模型下,研究了外汇期权定价问题,利用摄动方法给出了期权的近似定价结果。S.Corsaro构造了Heston模型网格查分的平行算法,并研究了亚式期权定价问题。 F.Soleymani研究了带有Hull-White随机率项的Heston模型,利用Feymann-Kac公式获取了相应的抛物偏微分方程,并给出了一种自Heston模型的适应网格划分算法。
二、目标任务
本课题在Levy噪声和分数Brownian运动驱动的市场环境下对金融市场上存在的理财产品进行数值定价分析,所得研究结果方便投资者和金融机构量化各种金融衍生产品的价值。本课题针对理财产品适合的偏微分方程初边值问题,进行网格差分,以期在特定的偏微分方程初边值问题的差分方法上获取更高精度的差分格式。
在Levy噪声和分数Brown运动驱动的Heston随机利率模型(以下简称“分数Levy-Heston模型”)下,本项目尝试以理财产品的定价问题为研究对象,以理财产品价值的网格划分为研究手段,找出理财产品价值的一个有效的差分格式,既能进行理论分析,也便于数值模拟。
三、主要内容
本项目主要研究那些分数Levy-Heston模型的金融理财产品的定价问题。具体地讲,我们将采理论推导和数值模拟相结合的方法研究理财产品的定价问题。
首先,基于网格差分方法,讨论分数Levy-Heston模型下、不附带提前实施条款的理财产品的定价问题,给出精度更好的迎风差分格式以及相应的稳定性、收敛性和相容性分析。
其次,讨论分数Levy-Heston模型下可自动续期类型的理财产品的定价问题。建立相应的变分不等式模型,计算其差分格式并讨论其自由边界(最佳实施边界)的性质。
最后,构造一种不依赖人工边界的并行算法。通常情况下,不依赖人工边界的差分算法只有显式差分格式,而显式差分格式往往是条件稳定的,本课题尝试构造一种并行差分格式,既满足无条件稳定又无需人工边界。
四、可行性分析
近年来,项目申请者一直从事期权定价方面的研究工作,并密切跟踪国内外在期权定价理论方面的研究现状,收集了丰富的数据资料,对相关期权定价理论和方法都进行了细致的分析,比较了解同类问题的研究现状和存在的问题。同时,项目申请者经常与项目成员进行讨论,对网格差分方法和Levy-Heston模型有了一定的了解,其研究思路已经基本熟悉。
本项目的研究思路是在以往期权定价理论的基础上,结合网格差分方法提出的,涉及的关键研究内容和研究路线是可行的,具体分析如下。
首先,用网格差分方法研究理财产品定价问题是可行的:许多理财产品定价问题经过Feymann-Kac公式或者金融资产的复制策略可以转化成各种形式的偏微分方程初边值问题。目前,项目申请人已经掌握了这些偏微分方程初边值问题的网格差分方法。
其次,对理财产品适合的偏微分方程的空间变量进行必要的转换是可行的: 项目申请人对这些偏微分方程的初边值问题已经有了细致的分析,通过何种方式进行转换,达到空间变量降维的效果,已有一定的了解。
最后,对差分格式进行稳定性、收敛性和相容性分析是可行的:网格差分有相对完善的稳定性、收敛性和相容性理论,项目申请人对这些也已掌握。

