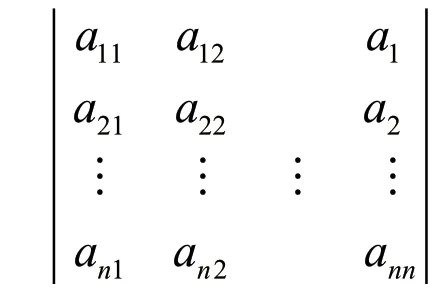行列式的几何意义探究

崔立功

（江苏财经职业技术学院，江苏淮安 223003）

0 引言

数学是人类探究世界，研究自然界任何事物的核心，数学比其他学科有更高的抽象性，这个也不是以人的精神和想象而转移的，而是实实在在的来源于我们的自然。如果我们教授数学，仅仅就是定理和公式的话，那么这就会让人感觉就是一堆冰冷的符号，难以产生热情，更加不会有火热的思考，但是授课教师掌握了蕴含在数学公式背后的思想和精神实质，那么就可以带领自己的学生畅游在知识的海洋里。把数学简单的当成一门公式堆积而成的学科来学习，而忽视数学的本质背景，这样的数学课程开设对学生的培养是无用的。

概念学习就要搞清楚概念的内涵和外延。而线性代数课程中概念的外延大内涵小的原因，进而学生们对它的理解容易发生偏差。鉴于这一特殊性，我们将借助于数学概念的几何背景来解释或者引入概念，有些概念我们要回到几何中的“根”上去找原因，显然这样的教学对教师的要求较高，但是对学生的理解是有帮助的。行列式的概念和性质很多同学学习了这个知识都感觉很简单，就是凭空的介绍了一个新的运算技巧，那么到底有什么意义，现在的教材上很少提及，当然有人会说为后面矩阵的计算特征值服务，为计算逆矩阵服务，我们所说是对的，但不是全部，我们看微积分的导数和定积分他们都有明确的几何意义，为这些知识在具体问题中的使用，打下了基础，可是行列式的几何意义是什么？绝大多少线性代数中并没有提及，本文就这个内容进行了研究。

1 预备知识

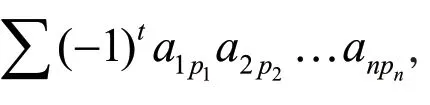
2 行列式的几何意义

定理一：一阶行列式|a|的几何意义是R数轴上数a到原点的有向距离，如果a≥0距离取正值，如果a＜0距离取负值。

证明：在数轴上当a≥0，|a|表示该数到原点的距离取正值，当a＜0，|a|表示该数到原点的距离取负值。

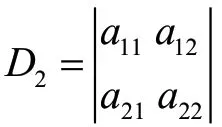
证明：如图1所示：以行向量α(a,a)与β(a,a)为邻边的平行四边形。

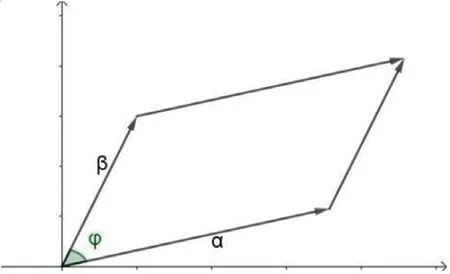
图1 二阶行列式几何意义图

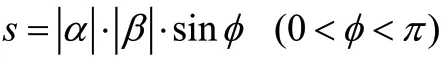
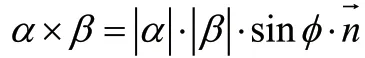
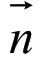
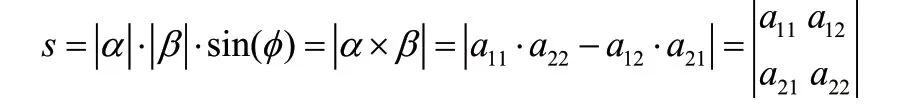
二阶即行列式的值等于平行四边形的面积，面积取正值。

二阶即行列式的值等于平行四边形面积，面积取负值。

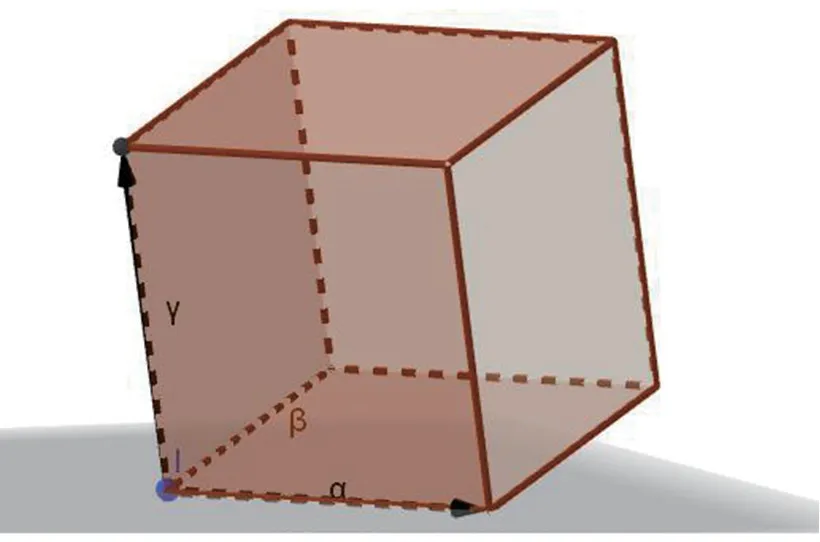
图2 三阶行列式几何意义图

三阶行列式即为空间平行六面体的体积，体积取正值。同理，当α,β,γ构成左手空间坐标系时，三阶行列式即为空间平行六面体的体积，体积取负值。

下面来分析n阶行列式情况，先定义一个超平面，再给出一个超平面的法向量。

定义1：设n-1个行向量a=(a,a,…a)，假设他们是共面的，则他们所在的面就为一个超平面。

定义2：由两个向量的叉积定义我们可知，新的向量为这两个向量所在的平面的法向量，所以我们定义这个超级平面的法向量为：

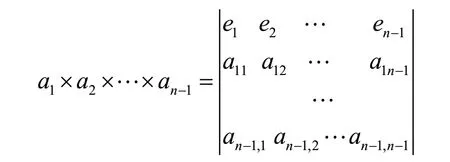
其中，e=(0,0,…1,…0)为单位向量。