Estimation based approximating control for wireless networked control systems

Liang Qipeng,Zhu Qiaohui,Kang Yu,Zhao YunBo*

1.College of Information Engineering,Zhejiang University of Technology,Hangzhou 310012,China;2.Department of Automation,University of Science and Technology of China,Hefei 230027,China

Abstract:The control design and system analysis of wireless networked control systems with unknown round-trip delay characteristics are investigated.An estimation based approximating control strategy is proposed to stabilize the systems by using delay characteristics in a practically feasible way.The strategy first uses a delay transition probability estimator to obtain the delay characteristics estimation by measuring delay data online,and then uses an approximating controller to take advantage of the estimation.On this basis,a packet delay variation detector is designed,making the strategy adaptive to the variation of delay characteristics.The sufficient conditions to ensure the closed-loop system being mean-square uniformly ultimately bounded are given,with also the controller gain design method.The effectiveness of the proposed approach is verified numerically.

Keywords:wireless network control systems;delay characteristics estimation;Markov jump system;approximating controller

1 Introduction

As a special class of networked control systems (NCSs),wireless NCSs (WNCSs)take advantage of wireless data communication networks to close the control loop.Thanks to the much more flexibility of wireless communications[1,2],as well as the developments of the embedded computing,sensing technology,etc.,WNCSs have become more and more influential in many next era information technologies including unmanned aerial vehicles[3],smart warehousing[4],Internet of vehicles[5],etc.[6-8].In these areas WNCSs can be regarded as their fundamental control architecture and hence play a vital role.

As is widely known how to effectively deal with the communication constraints such as network-induced delay,data packet dropout,etc.have always been central to the study of NCSs.For WNCSs,besides the unique features such as the flexible network topology,the security and privacy issues that are introduced by the wireless communications and have been investigated considerably in recent years,the aforementioned delay and dropout are still core to the design of WNCSs,but are more challenging for a different reason.

In fact,it is a naturally held belief that the more the information on the delay characteristics of NCSs is known,the better the system performance can achieve.Such a belief has already been demonstrated by many existing works.For example,under the assumption of time-varying delay within certain upper and lower boundaries,stabilized controllers can be designed[9-11],but with more information on the delay,e.g.,the probability distribution or the Markovian modeling of the delay,stabilized controllers can be designed subject to much larger upper and lower boundaries,and other performance index such as the settling time,overshoot,etc.can be further improved[12-14].

However,though the delay characteristics can be possibly known by classic wired NCSs,it is often not easy,if not impossible,to be known by WNCSs.The reasons are two-folded.Firstly,the flexibility of wireless communication networks means that nodes can easily join or leave the network,thus affecting the topology of the communication network that the considered WNCS uses,and consequently causing time-varying and hard to predict delays to the considered WNCS.This fact basically means that the exact delay characteristics can not be calculated even all the network parameters are known.Secondly,the wireless communication network used by the considered WNCS is usually of a relatively small scale since wireless communications are more unreliable,but the small scale further deteriorates the effects of the time-varying network topology,making the join or leave of a node affecting the delay characteristics greatly[15-17].

The above facts therefore mean that a better design for WNCSs will first require the appropriate measurement of the delay characteristics,since the system performance will be conservative without considering the detailed delay characteristics,which are however not directly available for WNCSs.

In order to deal with the above challenge,we propose an estimation based approximating control (EBAC)strategy to WNCSs.This strategy consists of a delay characteristics estimator at the controller side to estimate the delay characteristics by using online historical delay data,and a approximating controller to take advantage of the delay characteristics estimation.The sufficient stability conditions for the closed-loop system are given,and a controller gain design method is also proposed.Numerical examples illustrate the effectiveness of the proposed strategy.The remainder of the paper is organized as follows.Section 2 formulates the problem of interest,and the proposed strategy is then detailed in Section 3.The sufficient conditions for the stochastic stability of the closed-loop system with a controller gain design method are given in Section 4.Numerical examples in Section 5 validate the proposed approach and Section 6 concludes the paper.

2 Preliminaries and problem formulation

Consider the WNCS as illustrated in Figure 1,where the plant is described by the following linear discrete-time model with disturbances,

Figure 1.The considered wireless network control systems.

x(k+1)=Ax(k)+Bu(k)+Cw(k)

(1)

wherex∈n,u∈mandw∈are the system state,the control input,and the system disturbance,respectively,wwithwmaxbeing the upper bound of disturbance,andA∈n×n,B∈n×mandC∈n×mare the system matrices.

In Figure 1,the wireless communication network is shared with other users,and the sensors,controllers and actuators are time synchronized.The delay of sensor to controller and controller to actuator isdkandhkrespectively at timek.Time stamps are used in the data transmissions,and hence the actuator may know the round-trip delayτkat timek,by comparing the current time instant and the time stamp contained in the data reflecting the time instant when the sampled data was sent.

In WNCSs,τkcan usually be assumed to be unknown but behaves Markovian,as in Assumption 2.1.

Assumption 2.1(Markovianτk)The round-trip delaysτk,k≥1 are a Markov process with its unknown delay transition probability (DTP)being described by

(2)

whereπij>0,∀i,j∈

If we take consideration of nodes joining or leaving the network,we may find that in reality round-trip delay exist packet delay variation (PDV)[18],and PDV may exhibit a “piecewise Markovian”feature,that is,τkcan be essentially Markovian,but will be suddenly moved to another mode which is still Markovian,but with totally different transmission probabilities,as illustrated in Figure 2.This feature can be captured by Assumption 2.2.

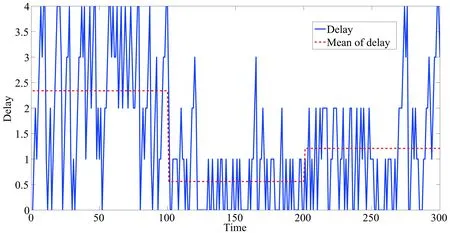
Figure 2.The transition matrix can be piecewise in practice.

Assumption 2.2(Piecewise Markovianτk)The PDV of round-trip delayτk,k≥1，is a piecewise Markov process,that is,the unknown transition probability matrix will be changed soon after the joining or leaving of the nodes at unknown time instants,but between two consecutive changes,the Markov process ofτkcan still be described as in Assumption 2.1.

Our goal is then to design appropriate control strategies for the system as illustrated in Figure 1 under Assumptions 2.1 or 2.2.One may realize that the key challenge here is that the characteristics of the round-trip delayτkis unknown,and therefore our approach will firstly try to estimateτk,which makes our work different from most existing works that often take the knowledge ofτkfor granted.

Figure 3.The framework of EBAC strategy in Assumption.

3 Design of EBAC strategy

In this section,we first design the EBAC strategy under Assumption 2.1,and then modify it to fit Assumption 2.2.

3.1 Design of EBAC strategy in Assumption 2.1

The control framework for the EBAC strategy is illustrated in Figure 3.By its name,one may realize that the main idea of our EBAC strategy is to approximate a more fine-tuned controller step by step,with the more accurate estimation of the delay step by step.For the EBAC strategy under Assumption 2.1,we have to design a DTP estimator to update the delay estimations,and an approximating controller to obtain the control signal.

In what follows we detail the designs of each module.

3.1.1 Design of the DTP estimator

One may understand that at the beginning of estimation the confidence can be worse than required due to the lack of samples.To deal with this challenge,we propose an improved Jeffery interval estimation method,as follows.

(3)

whereβ(c;d,e)is thecquantile of Beta distribution with parametersd,e,anda,bis the initial parameters of prior Beta distribution,usually taking the value of 0.5,Ni,kis the number of delays whose previous step delay isi,andXij,kis the number of received delay packets up to timekwith the delay values of two consecutive packets beingiandjrespectively.

The pair (Xij,k,Ni,k)can be obtained online iteratively.

(Xij,k,Ni,k)=

(4)

We then introduce a learning rate,σ≤1 to obtain a slowly narrowed estimation interval ofπijfrom [0,1] at the beginning,with the increase of samples,as follows,

(5)

where as can be seen,σbalances between the estimation interval and the estimation confidence,being an effective approach to solve the difficulty.

Remark 3.1The reasons for selecting the Jeffery interval estimation are two-folded.Firstly,the Jeffery interval guarantees an unbiased estimation,which is key to ensure the system stability.Secondly,the Jeffery interval estimation is a priori-based estimation method,which performs good in convergence for small quantity of samples[19].

3.1.2 Design of the approximating controller and actuator

At timek,the approximating controller receives the states setz(k-dk)=(x(k-dk),x(k-dk-1),…,x(k-dk-M)),and then the controller determines whether to update its gain,if

zT(k-dk)z(k-dk)≤c-1zT(ri)z(ri),c>1

(6a)

k-dk-ri>L,L≥M

(6b)

or

k-dk-ri≥Q

(6c)

whereriis theith updating moment,z(ri)is the updating states,Landcare configurable parameters,Qis the maximum allowed non-updating interval,whose value will be given in Section 4.

(7)

Remark 3.2The inequality (6a)ensure that the two consecutive updating statesz(ri)andz(ri+1)satisfy the decreasing relationship,which then help stabilize the system under certain conditions as given in Section 4.(6b)is used to adjust the update frequency:the largerLandcare,the greater the interval between two updating moments is.(6c)is used to keep the controller updating during the control process.

The state feedback control signal sequence is designed as follows[21],

U(k-dk)=[u(k-dk),…,u(k-dk+M)]

(8)

whereU(k-dk)with the time stampk-dkwill be sent to the actuator.

At the actuator side,the actuator selects fromU(k-τk)the control signalu(k)and applies it to the plant,

(9)

The EBAC strategy in Assumption 2.1 can then be summarized as Algorithm 3.1.

Algorithm 3.1The EBAC strategy for systems (1)with Assumption 2.1

2 The approximating controller judges whether the received states set meets equation (6),and then updatesU(k-dk)according to (8),and sends it to the actuator with time stamps.

3 The actuator receivesτk,selectsu(k)according to equation (9),and applies it to the plant.

3.2 Design of EBAC strategy for systems with Assumption 2.2

With Assumption 2.2,the PDV instants are unknown,and hence we design a PDV detector before DTP estimator to detect PDV instants,and restart Algorithm 3.1 after detected.The modified control framework for the EBAC strategy is illustrated in Figure 4.

Figure 4.The framework of EBAC strategy in Assumption 2.2.

Figure 5.The estimation interval as increasing number of samples use different σ.

Figure 6.The system states x1 and x2 with and without DTP estimator.

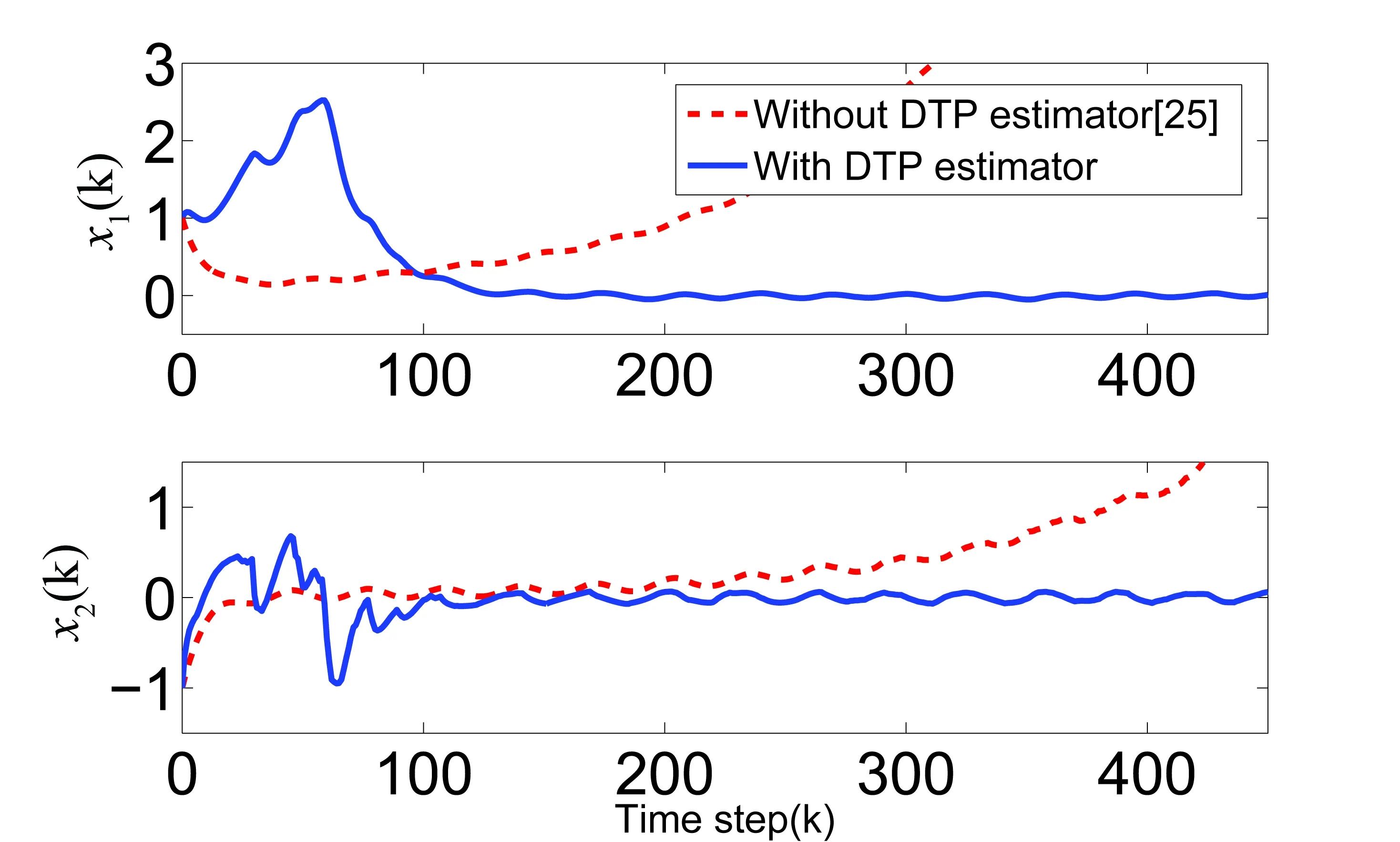
Figure 7 .The PDV happened at 400th step,and is detected at 436th steps.

Figure 8.The system states get by our method and method[26].

At timek,the PDV detector uses the latestwdelays to form the detection window,Dd={τj,k-dk-w

(10)

wherefiis the counts of each kind of delay inDd.We then compare it with chi-square distribution to obtain the detection result,see Reference [22] for details.The detect window will move one step forward when a new delay date arrives.

The modified EBAC strategy can be summarized as in Algorithm 3.2.

Algorithm 3.2The EBAC strategy for system (1)with Assumption 2.2

1 The PDV detector detects whether delay probability transition matrix has variation by equation (10):the algorithm goes to step 2 if there is no variation,otherwise goes to step 3.

2 Execute steps 1～3 in Algorithm 3.1.

3 Reset the system clock,and restart Algorithm 3.1.

4 Stability analysis and controller gain

design

Before proceeding further to the system analysis,we first present the following definition to be used later.

Definition 4.1[23]The trajectory of system (1)is said to be mean-square uniformly ultimately bounded (MUUB),if for any compact subsetDc⊂nand allx(0)=x0∈Dc,there exist a constant>0 and a time constantT=T(,x0),such thatE[xT(k)x(k)|x0] <,for allk>T.

4.1 Stability analysis

For the next stability analysis,we define the switching momentsi=k,k-1-τk-1

The following lemma is used to reveal the control signal used between consecutive switching momentssiandsi+1.

Lemma 4.1With the EBAC strategy,for any stepk∈[si,si+1),there existski∈[ri,si],such thatu(k)can be written as

(11)

(12)

Substitute equation(11)into the system (1),the closed-loop system can be written as

si≤k

The above expression can be rewritten as the following Markov jump system,

(13)

where

The following theorem gives the sufficient conditions of MUUB for the closed-loop system (13).

Theorem 4.1The closed-loop system (13)is MUUB under the EBAC strategy and Assumption 2.1,if there exist symmetric positive definite matrix setl={Pi,l,i∈} and symmetric matrix setl={Gi,l,i∈},such that the following LMIs hold for allrl,l≥0

(14)

Pi,l-Pj,l

(15)

λminI≤Pi,l≤λmaxI,∀i,j∈,

Q≥-(lnc+2lnλ)/lnρ

(16)

whereλmin,λmaxandρ<1 are given parameters,andλ=λmax/λmin.

For the closed-loop system in system (13),construct the Lyapunov function as follows,

V(z(k))=zT(k)Pτk,lz(k),

wherePτk,lis a positive definite matrix corresponding to each delay.Pτk,lis constant between the two switching moments.

We obtain

E(V(k+1)-ρV(k)-ρwT(k)w(k)|z(k),τk=i)=

ρzT(k)Pi,lz(k)-ρwT(k)w(k)

(17)

(18)

From equations (18)and (14),we can know equation (17)is less than 0,and thus

E(V(k+1)|z(k),τk)≤ρV(k)+ρwT(k)w(k)

(19)

Lemma 4.1 shows that the same controller gains sequence is used between two switching moments,and equation (19)can then be obtained as

(20)

From equation (20),The relationship between system states atkand at switching moment is shown in equation (21).

E(zT(k)z(k)|z(sl),τsl)<

(21)

Fromrltosl,the controller gains before update are used.Similar to the methods in equations (20)and (21),the relationship of states at switching moment and updating states can be obtained as follows,

E(zT(sl)z(sl)|z(rl),τrl)<

(22)

From equations (6a),(6c)and (16),the consecutive updating statesz(rl),z(rl-1)satisfy

E(zT(rl)z(rl)|z(rl-1),τrl-1)≤

(23)

Then from equations (23),(22),(21),we can obtain the following

(24)

(25)

Due to the constraint of equation (15),the control performance can be more improved when the estimation convergence.Consequently,we give the following theorem to ensure system (13)is MUUB without constraint (15),which is however relatively difficult to solve whenΠis completely unknown.

Theorem 4.2The closed-loop system (13)is MUUB under the EBAC strategy and Assumption 2.1,if there exist symmetric positive definite matrix setl={Pi,l,i∈},such that the following LMIs hold for allrl,l≥0.

(26)

(27)

where the definition ofλmin,λmax,λandρare the same as in Theorem 4.1.

4.2 Design of controller gain

Combining the advantages of these two theorems,the following controller gains design method is proposed.We introduceμ(k)to represent the convergence of the estimation.When all estimated interval width is less than a given thresholdθ,then the estimation is sufficiently close to the true value.

(28)

When the probability estimation does not converge,the controller gains are calculated by Theorem 4.1,or otherwise by Theorem 4.2.We propose Corollary 4.1 to obtain the controller gain.

Corollary 4.1The closed-loop system (13)is MUUB under the EBAC strategy and Assumption 2.1,if there exist symmetric positive definite matrix setl={Pi,l,i∈},symmetric matrix setl={Gi,l,i∈},and the controller gains sequenceK={K0,K1,K2,…,KM},such that the following LMIs hold for allrl,l≥0

(29)

(1-μ(kl))(Pi,l-Pj,l)

λminI≤Pi,l≤λmaxI,∀i,j∈

(30)

(31)

γij=

Remark 4.1The above analysis and design is for Assumption 2.1.This controller is still valid for Assumption 2.2,since as assumed the interval of PDV is sufficiently long,and each interval is regarded as an independent system mode.

5 Numerical examples

In this section,a numerical simulation example is used to illustrate the effectiveness of the proposed method.

Consider the system

x(k+1)=Ax(k)+Bu(k)+Cw(k),

xT(k)=(x1T(k),x2T(k)),w(k)is 0.1sin(2k),where the system state matrix is

with its eigenvalues being 0.8934 and 1.0166.The open loop system is unstable.The initial states of the system isτ0=1,x(0)=[1,-1]T.

The upper bound of the round-trip delayMis 4,and the delay probability transition matrixes is

which is unknown to the controller.

To verify the functions of the DTP estimator,takeπ23in the matrix as an example,whose actual value is 0.7.Figure 5 shows that when the number of delay samples is small,the traditional Jeffrey interval may not cover the true value.The improved Jeffery method can cover the true value without significantly slowing down the convergence speed(α=0.99).

To verify the EBAC strategy with Assumption 2.1,we compare our method with those in Reference [25].The parameters in Corollary 4.1 are set asρ=0.95,λmin=0.05,λmax=30,and the parameters in the EBAC strategy are set asL=4,c=1.1,θ=0.12.Figure 6 shows that our EBAC strategy can ensure the system convergence while the methods in Reference[25] destabilize the system.

To verify the EBAC strategy with Assumption 2.2,we keep the above system setting,and letΠbefore PDV be

Figure 7 shows that at 36th step after variation,the PDV detector restarts the DTP estimator,and the system starts the next round of control.Figure 8 shows that using the EBAC strategy with PDV detector can adapt to variation of delay characteristics,but the method in Reference [26] just uses the prior known matrix,and hence the stability of system can not be ensured.

6 Conclusions

For wireless networked control systems with unknown delay characteristics,an estimation based approximating control strategy is proposed,which is shown to be effective in realistic situations.It is worth pointing out that the proposed strategy is not only applicable to the delay characteristics under the Markovian assumption,but also applicable to other delay characteristics assumptions such as independent identically distributed delay and constant delay.This makes the proposed strategy widely applicable.In our future works we will try to reduce the computational cost to make the proposed approach more practically applicable.

Acknowledgments

The work is supported by the National Key Research and Development Program of China (2018AAA0100801),the National Natural Science Foundation of China (62173317),and the Key Research and Development Program of Anhui (202104a05020064).

Conflictofinterest

The authors declare no conflict of interest.

Authorinformation

LiangQipengreceived his BE degree from Xi’an University of Technology,China,in 2016.He is currently pursuing a Master degree at College of Information Engineering,Zhejiang University of Technology.His main research interests include wireless network control systems.

ZhuQiaohuireceived the BE degree from Tianjin University of Technology and Education,Tianjin,China,in 2018,and is currently a Postgraduate with Zhejiang University of Technology,Hangzhou,China.Her research interests include networked control systems and network security.

KangYureceived the PhD degree in control theory and control engineering from the University of Science and Technology of China,Hefei,China,in 2005.From 2005 to 2007,he was a Postdoctoral Fellow with the Academy of Mathematics and Systems Science,Chinese Academy of Sciences,Beijing,China.He is currently a Professor with the State Key Laboratory of Fire Science,Department of Automation,and Institute of Advanced Technology,University of Science and Technology of China,and with the Key Laboratory of Technology in GeoSpatial Information Processing and Application System,Chinese Academy of Sciences.His current research interests include monitoring of vehicle emissions,adaptive/robust control,variable structure control,mobile manipulator,and Markovian jump systems.

ZhaoYunBoreceived his BSc degree in mathematics from Shandong University,Jinan,China in 2003,MSc degree in systems sciences from the Key Laboratory of Systems and Control,Chinese Academy of Sciences,Beijing,China in 2007,and PhD degree in control engineering from the University of South Wales (formerly University of Glamorgan),Pontypridd,UK in 2008,respectively.He is currently a Professor with University of Science and Technology of China,Hefei,China.He is mainly interested in AI-driven control and automation,specifically,AI-driven networked intelligent control,AI-driven human-machine autonomies and AI-driven machine gaming.