雁列断层应力场影响因素数值模拟分析

王 时, 张环曦, 周安聘, 董 博, 章 阳, 纪春玲

(石家庄地震监测中心站, 河北 石家庄 050021)

0 引言

雁列构造是野外常见的一种间断、不连续的经典构造形式。众多学者对雁列构造进行了大量的研究工作,对断层的历史活动、相互制约和影响、地震机制以及前兆滑动过程等进行了分析和讨论。唐春安等[1]为了更好研究岩石的破裂过程,在考虑材料力学非均匀特点的基础上,对地震孕育过程进行数值模拟,并给出了应力场、变形场和微震活动的时空分布;郭玲莉等[2]通过对三种结构模型的黏滑实验,探讨了应力降与震级之间的关系,发现震源尺度是影响震级的重要因素;Dieterich[3]认为摩擦系数与时间具有一定的关联性,随着摩擦的增加,接触面积也在逐步加大,在垂直压力和接触强度不变的情况下,摩擦系数与接触面为正比关系,并用岩石摩擦实验证实了这个规律;王想等[4]认为岩石地震活动幕时段背景下需排除边界动力变化引起的区域应力场调整,再结合小震平静区或空间图像,判断平静属于岩石活动过程中出现的间歇平静还是震前平静异常;朱瑶宏等[5]研究了不同温度、动应力、初始偏应力、围压作用对黏土塑性应变的影响,发现影响因素的预测模型与试验吻合性较好;罗崇亮等[6]通过研究红层泥岩含水率对其力学特性及邓肯-张模型参数的影响,发现含水率对泥岩黏聚力和内摩擦角产生影响,进而导致结果出现差异;许健生等[7]对岩石进行了黏滑实验,发现岩石的黏滑错动分为三个部分,预滑、黏滑和止滑,黏滑过程是由多次黏滑错动过程组成;胡志平等[8]基于动三轴试验分析了不同围压条件下和加载方式对压实黄土应力应变关系的影响规律;王想等[9]利用传统和数字地震学方法,对震群与强震孕震关系进行了分析;任雅琼等[10]在实验室开展岩石变形实验,观测相关物理量的演化特征和规律,对压性雁列断层进行变形实验,根据应力时间曲线将具有前兆意义的变形阶段分为强偏离线性阶段、亚失稳阶段和失稳阶段,利用红外热像仪记录各个阶段的热场变化。但是影响雁列断层构造应力场的因素以及应力分布状态前人并未给出足够多的数值模拟实验,本文结合数值模拟做了一定的分析。

1 摩擦接触有限元数值计算方法

1.1 接触面力条件

由牛顿第三定律可知,接触面力应满足:

(1)

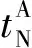
1.2 摩擦力的计算

接触面上的力:主要是摩擦力的计算,从节点N的法向接触力为fs,则它的最大摩擦力值为Fy=u|fs|,其中μ为摩擦系数。

设在上一时刻tn从节点ns的摩擦力为Fn,则当前时刻tn+1可能产生的摩擦力F*

F*=Fn-kΔe

(2)

式中:k是界面刚度;Δe是从节点的位移,

(3)

当前时刻tn+1的摩擦力Fn+1根据下式计算,

(4)

最后按作用与反作用原理,计算对应节点的摩擦力[2]。

2 模型的建立

本文建立了二条未贯通的二维理论雁列断层模型,分析了雁列走滑断层黏滑运动特征。图1为雁列断层有限元网格划分模型,在断层两侧做了加密处理,使计算精度进一步提高,在断层上选取了6个节点以便对比研究。该模型长160 km,宽90 km,该模型设置为均匀、各向同性,断层面为摩擦接触,这样可以更精确的计算断层黏滑运动的过程,下边界垂向固定,水平方向自由;左边界施加水平方向右的挤压,挤压速率为 1.2 cm/a,垂直方向自由;右边界水平方向固定,垂向自由。库伦摩擦定律被纳入塑性理论的研究范畴,基于弹塑性理论的返回映射方案已被应用到有限元摩擦接触分析,该方案使算法的收敛行为和可靠性产生了本质的提高。

图1 雁列断层有限元网格划分模型Fig.1 Finite element meshing model of the echelon fault

为了对比分析几何形态和黏滞系数对雁列断层黏滑运动的影响,建立了5个模型,分为了两组。第一组为基本模型1、模型2、模型3,是研究几何间距对断层黏滑运动的影响;第二组为模型4、基本模型1、模型5,是为了研究断层的黏滞系数对黏滑运动的影响,具体的模型列于表1(参考了西部地区的挤压速率及相关地质资料)。

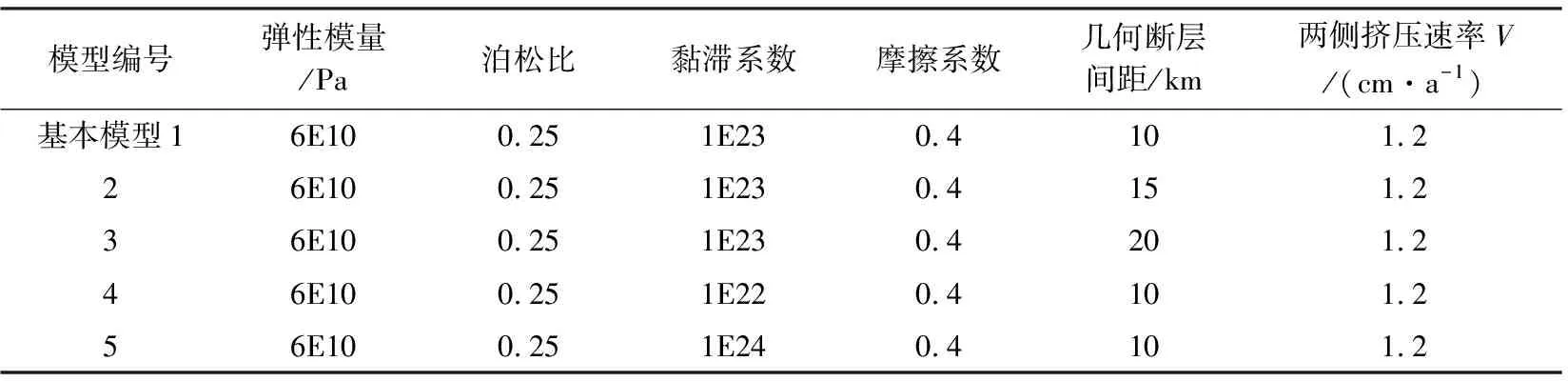
表1 模型的相关参数Table 1 Relevant parameters of the model

3 几何间距对断层黏滑运动的影响

3.1 几何间距与应力降之间的关系

图2展示了不同几何间距(10 km、15 km、20 km)情况下雁列断层的黏滑曲线。为了便于对比分析,选取断层相同位置分析几何间距对雁列断层黏滑运动的影响。曲线都是类似于阶梯式,曲线的平直段代表断层处于闭锁状态(黏着状态),断层两盘没有相对运动,剪应力处于积累状态,陡立段代表断层的突然滑动(活动状态),短时间内两盘有较大的相对位错,可以认为是一次地震的发生,形成应力降,应力减小。从曲线的变化情况可知,3个模型中断层两盘的相对运动都是黏着状态与滑动状态的交替发生。

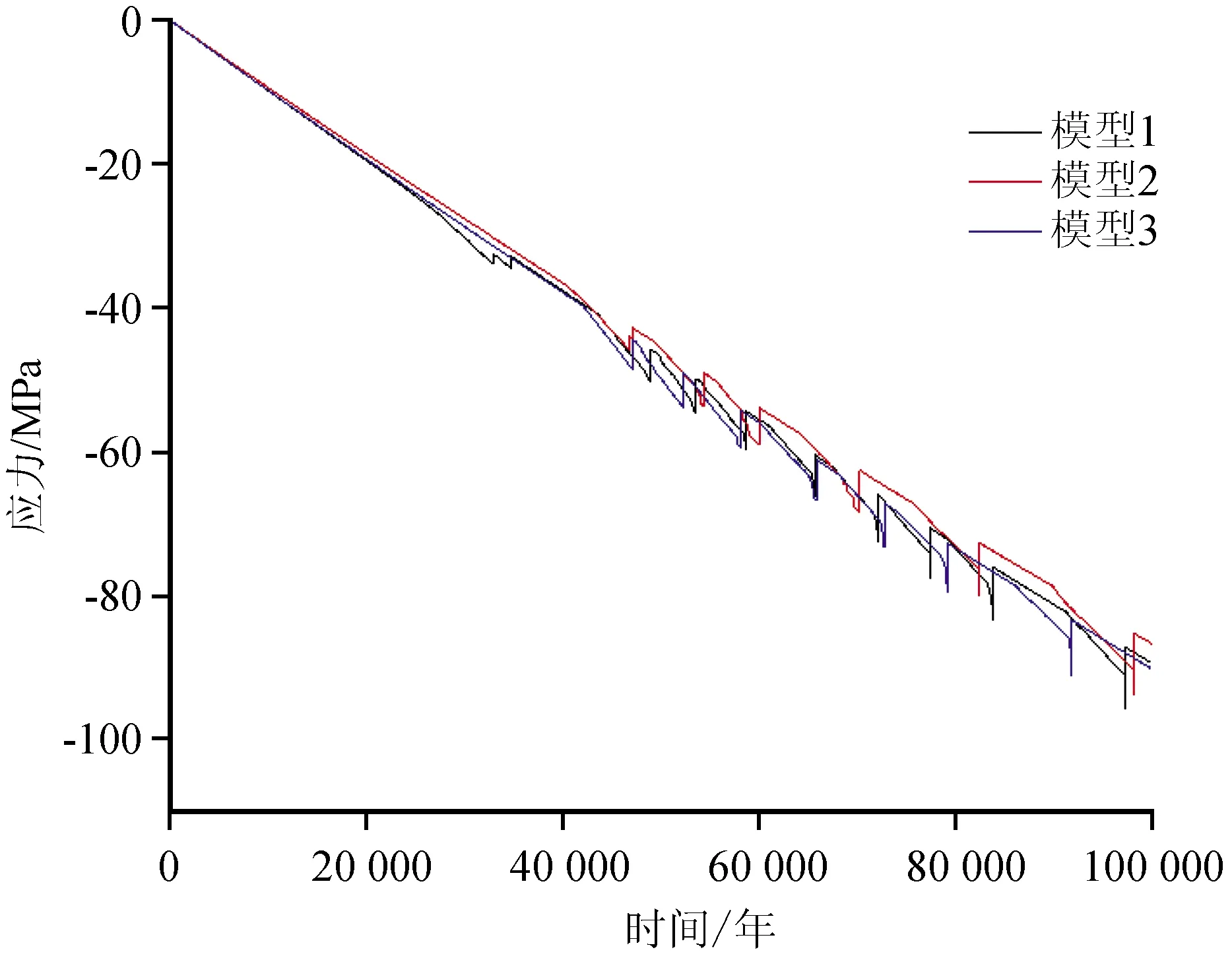
图2 不同几何间距的剪应力随时间变化曲线Fig.2 Time-dependent curves of shear stress with different geometric distances

总的来看,三个模型的都处于应力积累的状态。但断层几何间距越小,断层相互之间的控制力越强,应力场较大,容易发生黏滑运动,故而地震较多;几何间距增大,断层之间控制力较弱,构造应力场较弱,断层受到的应力较小,故黏滑运动较为平稳。当断层向前滑动时,剪应力被释放,同时产生地震并形成相应的应力降。由此认为,沿断裂面发生黏滑时,一次地震就是与断裂黏滑有关的一个应力降,从而解释了地震时应力降低的现象。地震时断层位错越大,产生的应力降也越大。对于不同的几何间距,地震时的应力降也各不相同,当几何间距为10 km(模型1)时,地震产生的应力降最大约为10 MPa,当几何间距为15 km(模型2)时,应力降最大约为8.5 MPa,当几何间距为20 km(模型3)时,应力降最大约为6.5 MPa。

3.2 应力与应变之间的关系

如图3所示,当几何形态变化从10 km到20 km逐渐增大时,断层的应力和应变均逐渐降低,是因为断层间距过大,断层之间的相互作用力降低,构造应力场变小的缘故。当几何间距为10 km时,断层的应变和应力值最大,应变量超过3E-5有6次,几何间距为15 km时,超过3E-5有2次,当间距为20 km时,超过3E-5有1次,由图可以看出,几何间距越小,应变量较大的次数较多,容易发生震级较大的地震,几何间距越大,应变量较小,但是频率高,容易卸载剪应力,应力不能持续积累,故而结构较为稳定,发生较大震级的地震的可能性小。

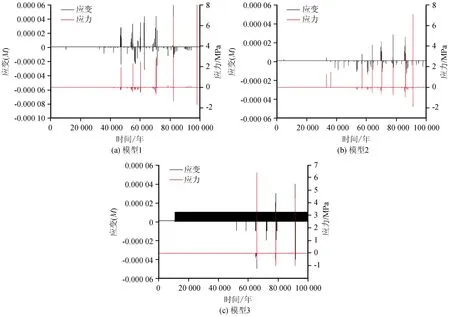
图3 模型应力与应变随时间的变化关系Fig.3 Variation of model stress and strain with time

3.3 几何间距与剪应力变化云图

图4是断层第3 000步、6 000步和10 000步的应力变化云图。每一个子步即每一个阶段的应力值是不同的,且断层的应力分布是不均匀的,应力集中在贯通区域(即岩桥区),由中间向两边依次减小。当几何间距为10 km、15 km、20 km时,断层之间的最大应力分别为0.255E9、0.242E9、0.23E9。可见,随着间距的增大,断层之间相互的影响力在逐渐减小。

图4 模型1～3雁列断层剪应力随子步变化的应力云图Fig.4 Nephogram of shear stress variation of echelon fault with sub step in model 1～3

3.4 几何间距与应力分量之间的关系

图5中第一层、第二层、第三层分别为第一、第二、第三主应力的应力云图(应力分量图的排序与表2所示内容一致)。可以看出,第一主应力主要集中在断层的贯通区域,与断层面相互垂直,随几何间距的增大,断层之间的应力逐渐减小,趋于平静;第二主应力与断层呈40°～ 45°夹角,离贯通区域越近,应力值越大,越远离该区域,应力越小;第三主应力主要分布在断层本身,即断层本身主要受到第三主应力的影响,而非第一和第二主应力,断层的受力呈现不均匀趋势,在断层末端受力最小,断层的岩桥区应力最大。

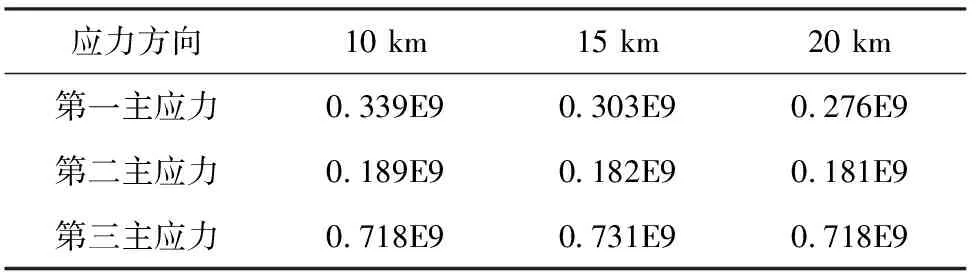
表2 应力分量与几何间距之间的数值模拟

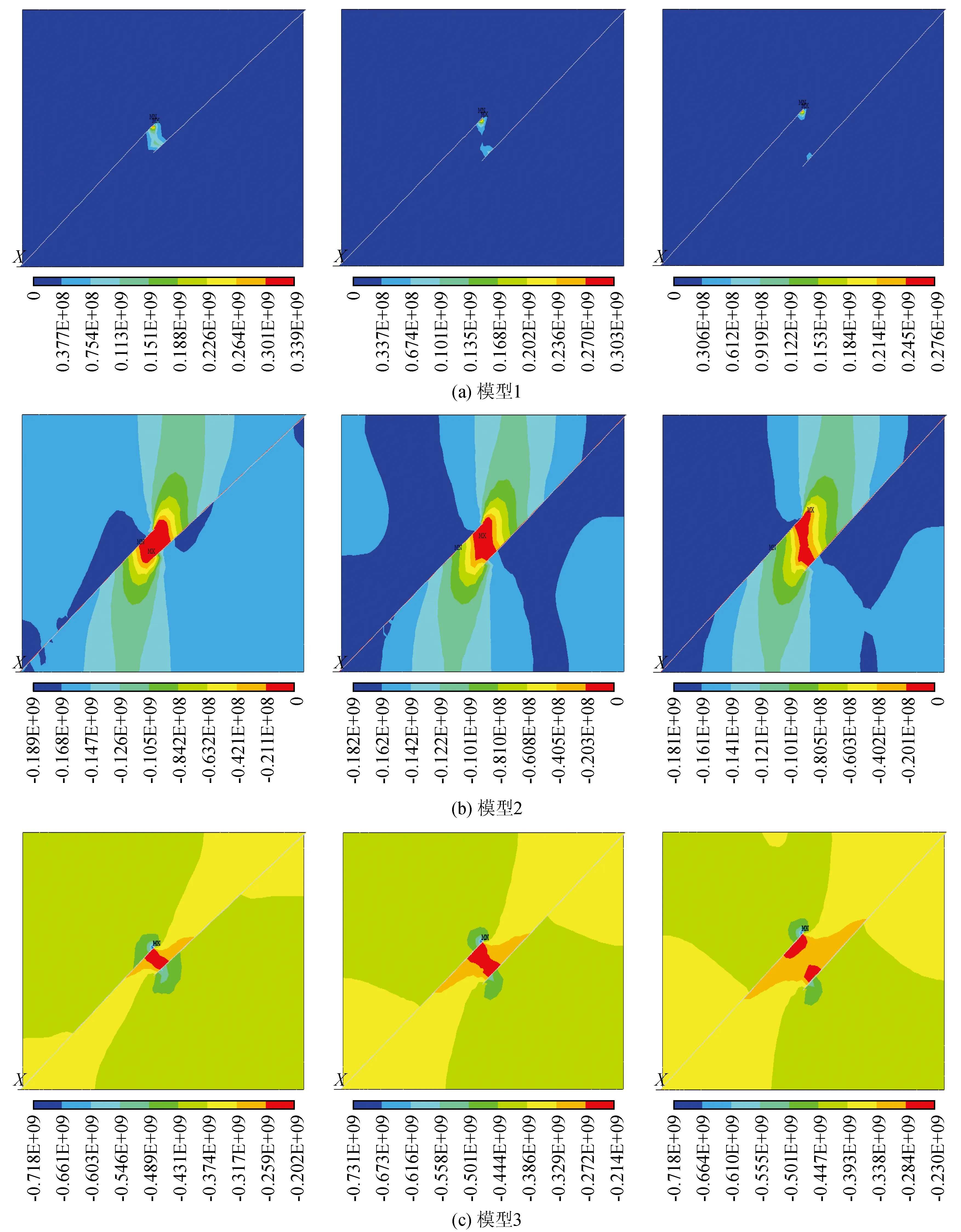
图5 模型1～3在几何间距影响下应力分量的应力云图Fig.5 Stress component nephogram of model 1～3 under the influence of geometric spacing

如图6所示,通过对不同模型雁列断层的横向对比可以看出,随着几何间距的增大,第一和第二主应力呈现下降的趋势。而第三主应力则呈现对称的形式,即在15 km处断层的第三主应力最大,断层的结构相对不稳定,易发生滑动位移,从而产生地震。

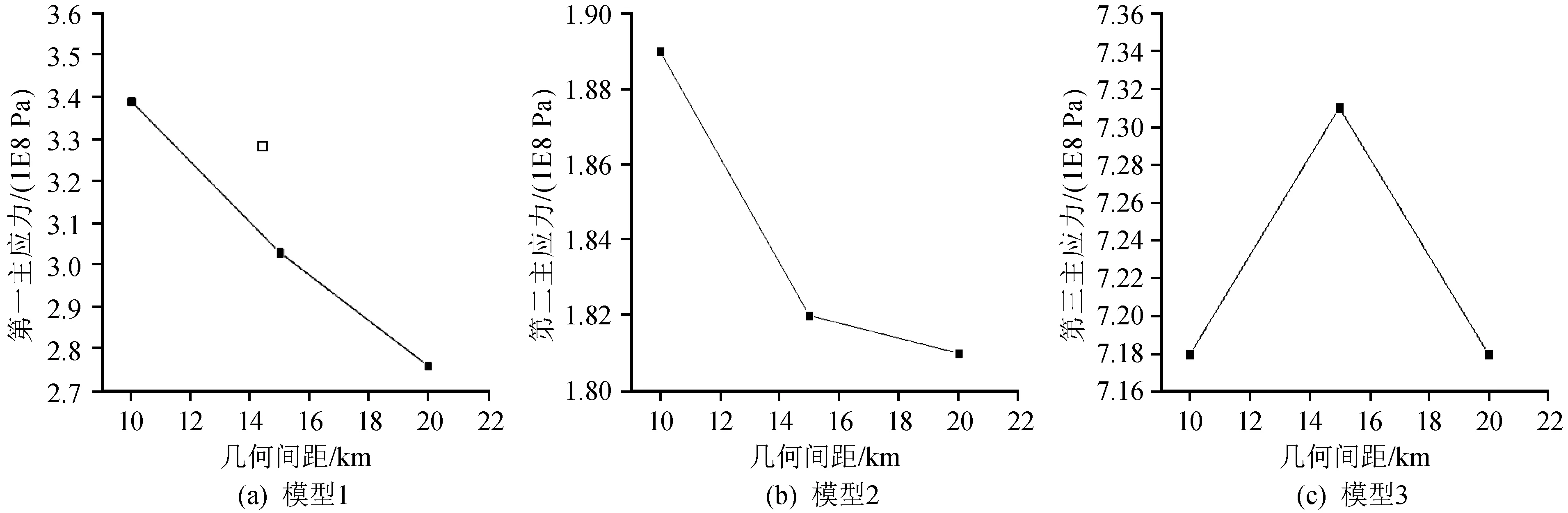
图6 模型1～3主应力与几何间距之间的关系Fig.6 Relationship between principal stress and geometric distance in model 1～3

4 黏滞系数对雁列断层黏滑运动的影响

4.1 黏滞系数与应力降之间的关系

为了分析黏滞系数对雁列断层黏滑运动的影响,本章采用了第二组模型,即模型4(1E22)、基本模型1(1E23)、模型5(1E24),选取了相同的区域进行对比,三组雁列断层的主要模型参数相同,具体参数见表1。

由图7可知黏滞系数越大,断层之间的应力值越大,当发生黏滑运动时,产生地震,形成的应力降也较大,当黏滞系数为1E22(模型4)时,地震产生的应力降最大约为4.5 MPa,当黏滞系数为1E23(模型1)时,应力降最大约为8.5 MPa,当黏滞系数为1E24(模型5)时,应力降最大约为9.5 MPa。

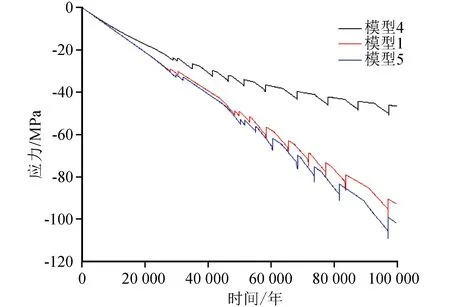
图7 不同黏滞系数的剪应力随时间变化曲线Fig.7 Time varying curves of shear stress with different viscosity coefficients

4.2 应力与应变之间的关系

如图8所示,当黏滞系数从1E22到1E24逐渐增大时,断层的应力和应变是两种不同的情况,应力是逐渐上升而应变则呈现下降的趋势。当黏滞系数较大时,断层结构较为稳定,应变较小,而应力一致处于积累状态,故应力值较大、应变量小。当黏滞系数较小时,结构松散,容易发生较大的应变,形成应力降,应力能被卸载故而不能累积,故应力值较小、应变量较大。

由图可以看出当黏滞系数为1E22时,应变量超过3E-5的有4次;当黏滞系数为1E23时应变量超过最大值3E-5的有4次;当黏滞系数为1E24时,应变量超过最大值3E-5的有0次。当黏滞系数越小,应变越大,越容易发生震级较大的地震。黏滞系数越大,断层较为坚固,不易发生形变,但应力不断持续累积,平时容易发生较小的变形,发生震级较小的地震,当应力值积累到一定的程度,超过岩石的承受极限时,发生大的应变,就会发生震级较大的地震。

4.3 黏滞系数与剪应力变化云图

图9为各雁列断层剪应力在第3 000步、6 000步和10 000步的剪应力变化云图,随着子步的变化,断层的剪应力也在发生改变,每一子步即是一年,可以看出黏滞系数的改变不会影响断层的应力分布,即断层的空间区域不同,受到的应力也不同。

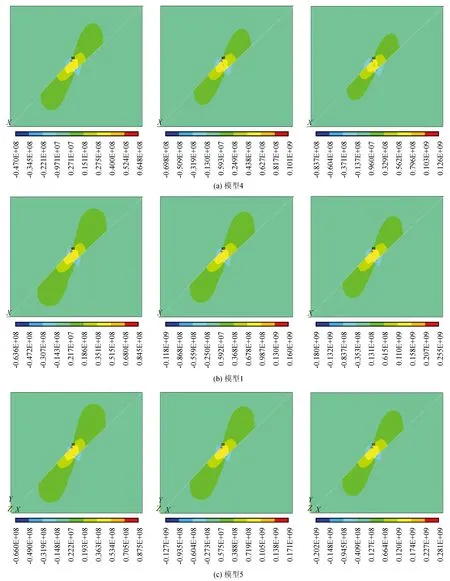
图9 各类模型雁列断层剪应力随时间变化的应力云图Fig.9 Shear stress nephogram of echelon fault with time in various models

当黏滞系数为1E22～1E24时,断层的最大应力值分别为0.126E9、0.255E9、0.281E9。当其他参数条件不变,随着黏滞系数的增大,断层之间的应力不断积累,应力值逐渐增大。

4.4 黏滞系数与应力分量之间的关系

图10为主应力分量的应力云图,其排列顺序与表3所示内容相同。从图可以看出,随着黏滞系数的增大,第一、第二、第三主应力逐渐增大且第一主应力与断层垂直;第二主应力与断层呈40°～ 45°夹角;第三主应力与断层平行。

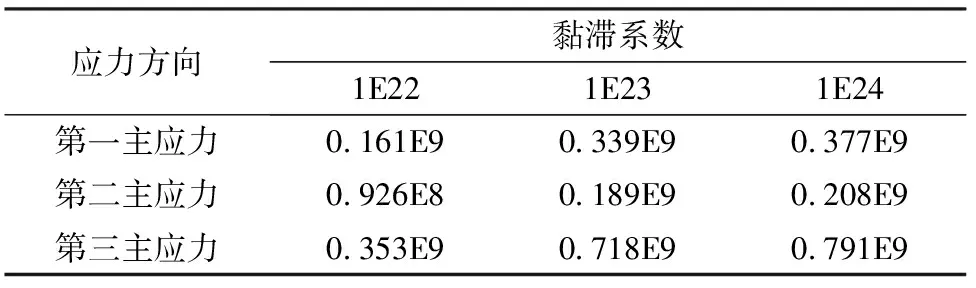
表3 应力与黏滞系数之间的数值模拟

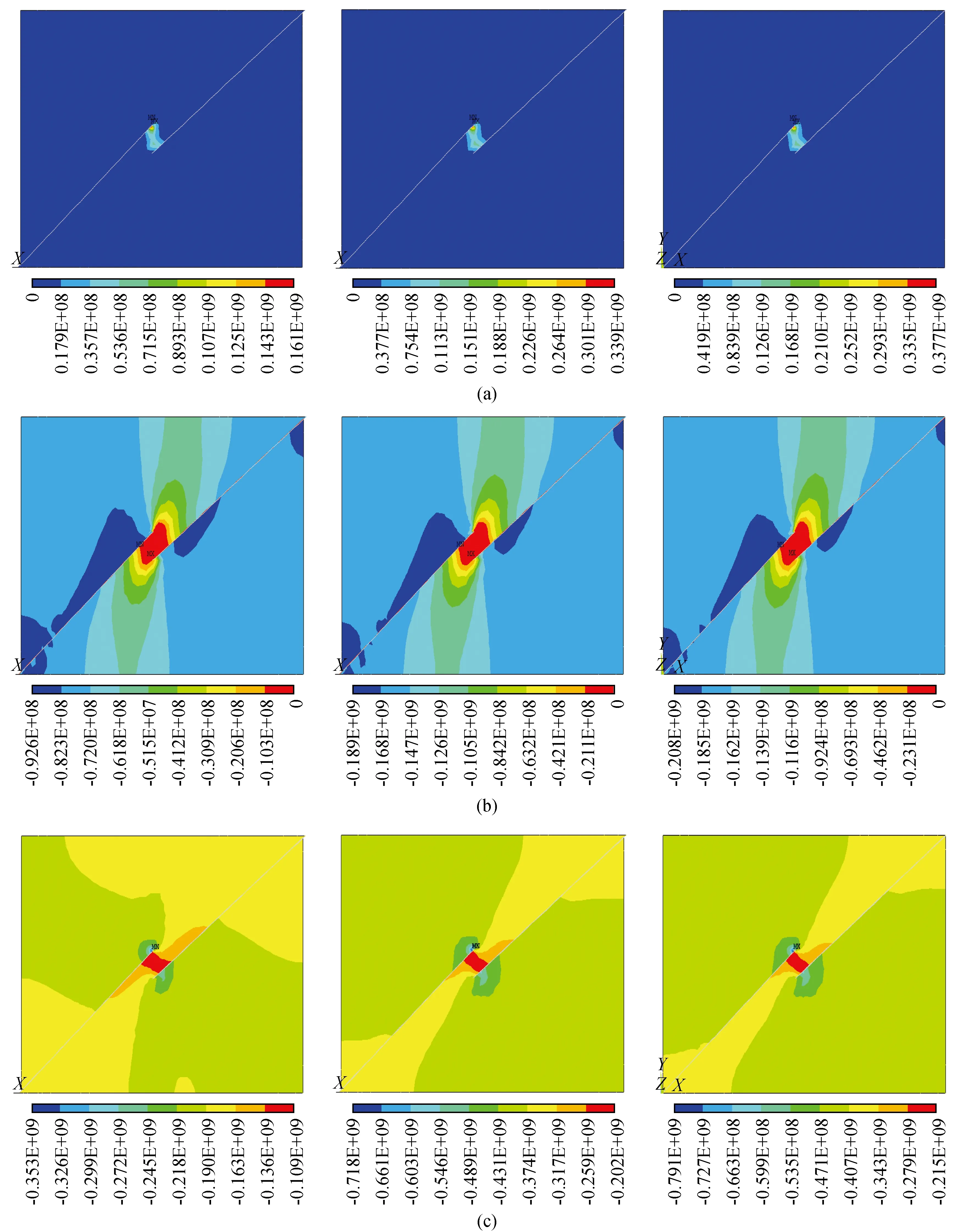
图10 在黏滞系数影响下各应力分量的应力云图Fig.10 Nephogram of each stress component under the influence of viscosity coefficient

如图11所示,通过对不同模型雁列断层的横向对比可以看出,随着黏滞系数的增大,断层的第一主应力、第二主应力和第三主应力逐渐增大,符合断层的剪应力变化和应力-应变之间规律相符合。

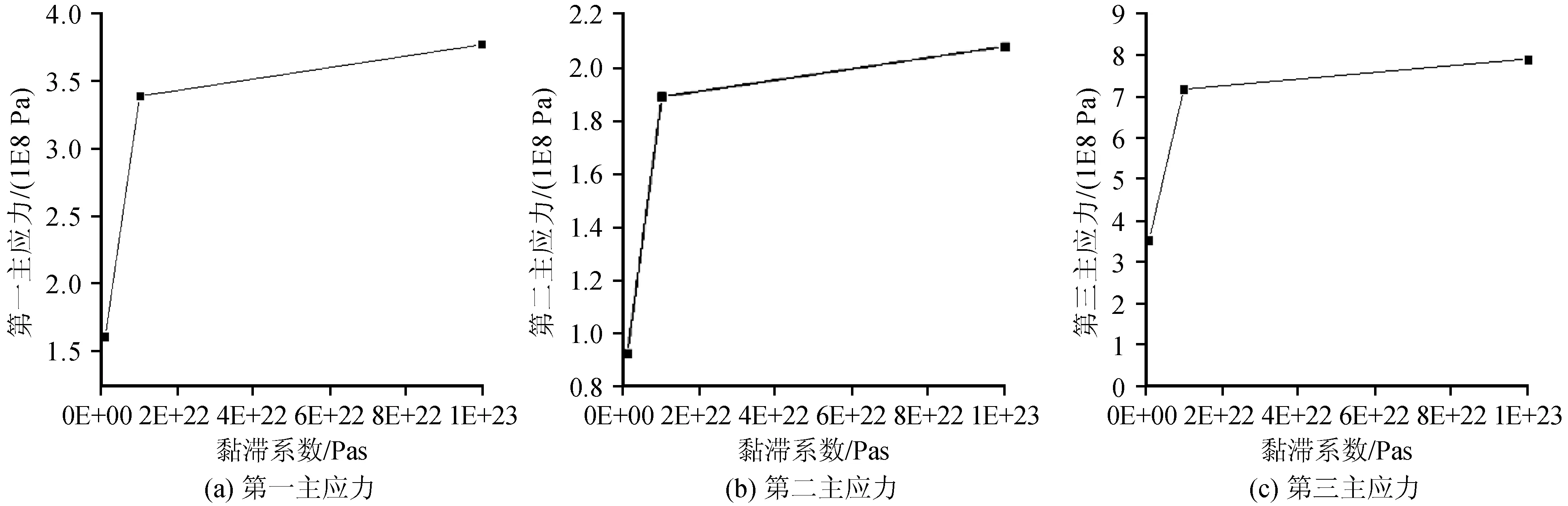
图11 各黏滞系数与应力之间的关系Fig.11 Relationship between viscosity coefficient and stress

5 结论

通过对比的方法可以看出,断层的几何形态和黏滞系数是影响雁列断层黏滑活动的重要因素,但这两个因素不会影响断层应力分布不均匀的状态。

(1) 断层的几何间距在10～20 km之间时,随着间距的增大,断层之间的相互控制力在逐渐减小(应力和应变减小),不易发生震级较大的地震,断层之间的活动相对平缓。

(2) 当黏滞系数在1E22～1E24范围之间波动时,黏滞系数越小,结构越不稳定,易发生错动从而产生地震,并伴随应力降的产生;当黏滞系数较大时,结构较为坚固,不易发生较大变形,但应力在不断地积累,积蓄的应力值逐渐增大,一旦积累到一定程度超过岩石的承受极限,岩石就会发生破碎形成震级较大的地震,但这需要一个较长的地震周期。

(3) 断层的空间区域不同,受到的应力也不同,越接近岩桥区域,受到的应力越大,由岩桥区域向断层的两侧逐渐延伸,受到的应力依次减小,体现了断层空间区域受力不均匀。应力在断层的岩桥区域最为集中,两端的应力较小,摩擦较为平缓。

(4) 第一、第二、第三主应力与断层呈一定的角度,第一主应力控制断层的岩桥区域,第二主应力控制断层的应力向外延伸,与断层呈40°～ 45°夹角,第三主应力主要控制断层本身。