基于互补滤波的汽车姿态数据采集系统研究*

张新宇

(辽宁省交通高等专科学校轨道交通工程系,辽宁 沈阳 110122)

随着汽车行业的快速发展,汽车监控系统越来越受到重视,汽车监控系统一方面可以监督驾驶员的驾驶行为,另一方面,也可以在发生事故后,进行事故回放,判定事故责任,保护驾驶人员的合法权利。

近年来,广泛应用于无人机领域的MEMS 传感器,由于其体积小、成本低、集成度高、精度高,逐步在汽车监控领域得到了应用。但是MEMS 传感器由于自身的特点,存在难以克服的噪声误差,因此,必须采取相应的算法,来消除噪声误差。刘军等[1]中使用六轴传感器,实现汽车运动姿态测量,采用卡尔曼滤波算法消除误差,由于重力加速度的存在,加速度计无法修正陀螺仪的航向角,卡尔曼滤波算法比较复杂。王京等[2]中使用三轴加速度计,采用改进的遗传神经网络算法消除误差,实现汽车姿态测量,但是三轴加速度计无法计算航向角,算法也比较复杂。曹景伟等[3]使用陀螺仪和加速度计,利用卡尔曼滤波算法将MEMS 陀螺仪和加速度计输出的数据进行滤波融合。但没有使用磁强计数据,无法修正航向角,无法解算出准确的全方位姿态角。且算法比较复杂。李超[4]使用陀螺仪、加速度计和磁强计,主要研究线性加速度的干扰,误差方程采用卡尔曼滤波算法。算法比较复杂。王贇贇[5]使用三轴加速度数据、三轴角速度数据和三轴地磁数据,采用一种基于粒子滤波的条件式姿态解算算法,获得姿态角,采用非线性扩展卡尔曼滤波进行数据融合。算法比较复杂。

因此设计了一种基于互补滤波的汽车姿态数据采集系统,采用互补滤波数据融合算法,解算出全方位的姿态数据,为监控汽车的运行状态提供一种新的手段。

1 惯性导航原理

惯性导航是一种自主式定位方法,它是利用加速度计、陀螺仪和磁力计实时测量物体的线运动、角运动以及其他外界的运动信息,根据运动特性和惯性微分方程,并在给定初始条件下,推算运动物体的位置、速度和运动姿态信息。

运动姿态的表示方法有方向余弦、四元数和欧拉角。欧拉角在求解姿态时存在奇点,不能用于全姿态的解算；方向余弦可用于全姿态的解算,但是计算量较大,不能满足实时性要求。四元数计算量小,无奇点,可以满足汽车运动过程中姿态的实时解算。因此采用四元数来进行姿态解算。

由于使用陀螺仪、加速度计和磁力计单独计算姿态信息,都有各自存在的无法规避的物理缺陷:使用陀螺仪测量值计算,积分过程中容易产生较大的累积误差,使用加速度计测量值计算,无法分离加速度测量值中的重力分量与运动分量,使用磁力计测量时,容易受到环境中磁场干扰的影响,这3 种误差在使用过程中是无法预先消除的,所以就必须要使用相应的数据处理方式来最大限度上消除单一传感器产生的误差。

陀螺仪和加速度计的姿态信息成互补性,可以采用滤波的方法进行加权平均,取得最好的估计结果。常用的方法有卡尔曼滤波和互补滤波。

卡尔曼滤波[6]是一种对系统状态进行递推最优估计的算法,它使用观测信息以及前一时刻的最优估计值作为系统输入,来估计该时刻的状态量。卡尔曼滤波的权重有一个逐步收敛的过程,计算量较大,而且需要对待测变量的误差模型有一个准确的估计。

互补滤波法[7]是根据不同传感器的各自特性,即加速度计/磁力计具有高频噪声(需要低通滤波),陀螺仪具有低频噪声(需要高通滤波),通过高通或低通滤波器来滤波,然后再进行组合来进行数据的融合。互补滤波的权重固定,不需要对误差模型做过多估计,计算量较小,因此采取互补滤波算法。

2 系统总体设计

汽车姿态数据采集系统分为车载单元和上位机单元。车载单元主要由嵌入式处理器、运动传感器、北斗模块和存储模块组成。处理器将运动传感器采集到的九轴数据进行融合解算,得到有效的姿态信息,结合北斗模块定位信息和时间信息,以固定格式保存到存储模块中。

3 系统硬件设计

本系统采用基于ARM Cortex -M4 内核的STM32F407ZGT6 高性能处理器,其时钟频率达到168 MHz,功耗低,具有更快的模数转换速度、更强大的输入/输出端口。传感器采用六轴MPU6050 和三轴磁力计 HMC5883L。定位模块采用北斗ATGM336H。存储模块用来把数据保存到U 盘中。如图1 所示。

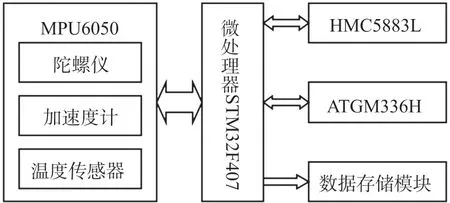
图1 系统硬件框图

4 汽车姿态数据解算

惯性器件都有各自的缺点和局限性,单一使用任何传感器,都无法得到有效准确的姿态信息。因此,需要利用多个传感器之间存在性质互补的特点,将多个传感器数据融合到一个单一的、最优的姿态估计中[8],从而得到最准确的姿态数据。

数据解算流程图如图2 所示。

图2 程序设计流程图

4.1 九轴数据校准

三轴加速度计、三轴陀螺仪、三轴磁力计的读数都会有偏移的现象,数据并不是围绕着静止的工作点摆动,因此,有必要校准九轴数据[9]。

三轴陀螺仪的校准是相对简单的工作,只要找到摆动的数据围绕的中心点。在静止状态时,陀螺仪的X轴、Y轴和Z轴读数理论上应为0,但往往会存在偏移。

通过计算机串口读取一段静止时的三轴陀螺仪读数,将这三组读数用统计均值的方式获取偏移量,每次的读数都减去偏移量就可以得到校准后的数据了。

加速度计的校准需要将设备置于水平、坚固的平面上。加速度计的X轴和Y轴的理论值应为0,加速度计的Z轴的理论值应为-16 384(假设加速度计设定为2 gn,g的加速度的读数应为最大值-32 768的一半)。

通过计算机串口读取一段时间的三轴加速度数值,由于加速度计的X轴和Y轴的理论值应为0,这2 个读数偏移量可以用统计均值的方法求得。加速度计的Z轴统计偏移量时,每次读数都需要加上16 384,再进行统计均值计算。之后每次都减去偏移量就可得到比较准确的三轴加速度值。

磁力计的校准[10-12],如果磁力计平放着绕Z轴旋转一周,读回的X轴和Y轴2 个轴的数据组成的点,理论上会形成一个圆,而实际上却是一个椭圆,并且中心点不在原点,此时使用航向角公式算出的角度是不准的,如果想用航向角公式的话,需要把这个偏移的椭圆校正成中心点在原点的正圆。校准的输出可以根据下面的方法来计算:

通过计算机串口收集磁力计被旋转360°后的数据。对采集到的数据进行分析,找到磁力计X轴、Y轴以及Z轴的最大值和最小值,xmax,xmin,ymax,ymin,zmax,zmin。

于是可以得到X轴的偏移值为:

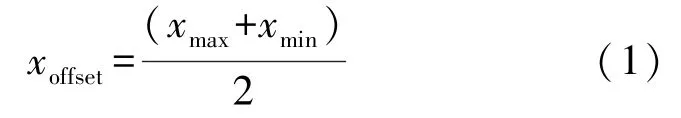
因为只需要方向,所以可以设X轴的比例系数xgain为1。

Y轴的偏移值为:

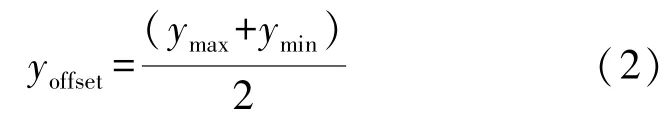
Y轴的比例系数可以由下式计算。

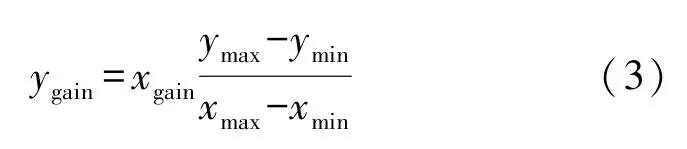
Z轴的偏移值为:

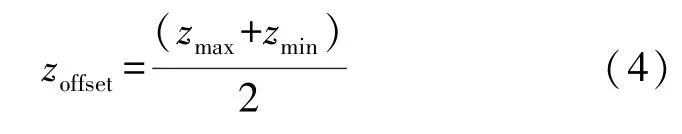
Z轴的比例系数可以由下式计算。

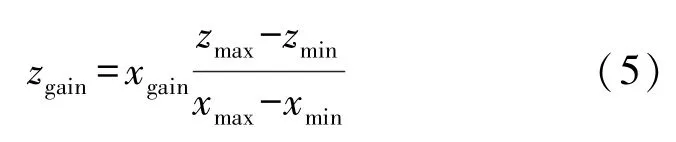
磁力计可以由下式校准。

4.2 九轴姿态解算

陀螺仪可获得角速度,通过积分可获得角度,但随时间累积,积分漂移误差会越来越大,陀螺仪响应速度快,表现为低频特性,误差随时间累积。

加速度计对载体的加速度敏感,动态响应较慢,表现为高频特性,测量倾斜角时,短时间误差较大[13]。

通过互补滤波将陀螺仪和加速度计的优点结合起来[14],可以在低频段和高频段得到较好的信号,有效提高姿态输出精度。

标准重力加速度gb从导航坐标系n系转换到载体坐标系b系中的四元数表示的矩阵为:

式中:vX、vY、vZ是标准重力加速度gb的X轴、Y轴、Z轴分量。q0、q1、q2、q3是四元数中的实数分量。

加速度计测得的三轴加速度ab在b系中的矩阵表示为:

式中:ax、ay、az是三轴加速度ab在X轴、Y轴、Z轴分量。

gb和ab都是b系的向量,经过归一化处理后,模长为1,gb和ab向量叉乘的大小仅与sinθ有关,当角度很小时,叉乘结果可以近似于角度成正比。这个结果可以作为给陀螺仪的校正补偿值。公式为:

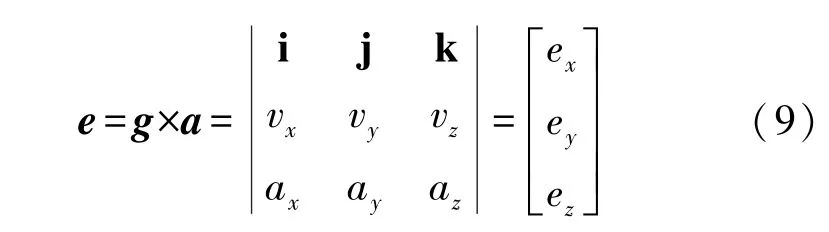
利用PI 控制器进行互补滤波处理,消除偏移误差。

PI 控制的公式为:

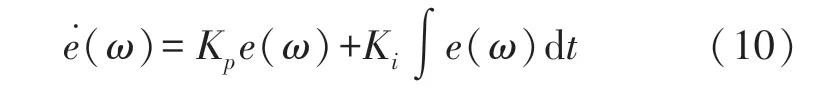
式中:ω是陀螺仪输出的角速度,是陀螺仪的校正补偿值。

只要误差存在,PI 控制器就会持续作用[15],直到误差为0。控制的效果取决于P 和I 的值,分别对应于比例控制和积分控制的参数。PI 控制器参数获取的具体方法为,先设定积分控制系数Ki为0,将系统变为纯比例调节,然后将比例控制系数Kp值由零开始逐步增大,直到系统出现振荡,再反过来调节将Kp值逐渐减小,直到系统振荡消失,记录当前的比例控制系数Kp值；当比例控制系数值确定后,设定一个比较大的积分时间常数Ti,逐渐减小积分时间常数,直到系统出现振荡,再增大积分时间常数Ti,直到系统振荡消失,记录当前的积分时间常数Ti值,积分控制系数Ki就等于Kp除以Ti。

将补偿值加到三轴陀螺仪输出的数据上进行数据修正、融合[16]。

将融合后的陀螺仪数据通过四元数微分方程转化为四元数输出。

式中:T为采样周期。

将得到的四元数转化为姿态角。

互补滤波解算法流程如图3 所示:

图3 互补滤波解算法流程图

4.3 航向角修正

上面的互补滤波法因为没有参考量,无法计算出当前的航向角γ的绝对角度,只能得到航向角γ的变化量,也就是陀螺仪的Z轴的角速度。可以通过对陀螺仪Z轴角速度进行积分,来计算当前航向角γ。由于测量精度以及温度影响的问题,并且,随着时间的推移,计算值会产生累积误差,长时间后就完全失去了意义。

加速度计可以取得与地球重力相关的横滚和俯仰方向的姿态信息,可以用来修正陀螺仪的横滚角和俯仰角,但是加速度计无法测量重力方向(即Z轴方向)的旋转,无法计算出航向角,无法修正陀螺仪的航向角。因此需要加入磁力计HMC5883L 来解决这个问题,得到3 个轴的准确姿态信息。

水平放置时航向角可由下式得到:

式中:MY和MX是磁力计的Y轴和X轴分量。

单独使用磁力计时,无法保证磁力计水平放置,导致测量的航向角有较大误差,通常利用加速度计来修正磁力计的倾斜角。

非水平放置时通过MPU6050 获得俯仰角(ψ)和翻滚角(θ)对航向角进行倾斜角补偿,公式如下:

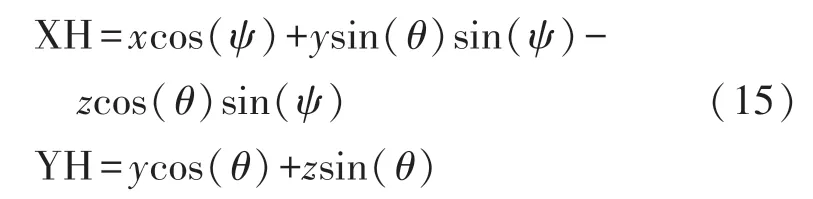
非水平放置时航向角公式为:

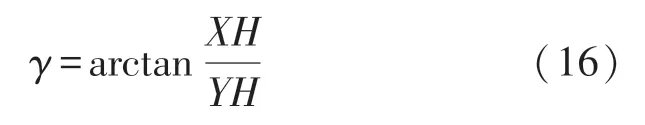
5 试验验证

将本系统固定在汽车上,在汽车运行过程中,采集汽车运行姿态数据。上位机采用MATLAB 的GUI 功能进行设计,通过读取系统中存储的以时间命名的文本文件数据,其中存储着时间、加速度、角速度、磁向量、温度、海拔高度、行驶速度等数据信息。在上位机界面上以曲线的形式把汽车的运行轨迹描绘出来。经过对比,能够真实地反映出汽车的运行状态。

图4 所示是以时间为X轴,三轴加速度为Y轴的曲线图。

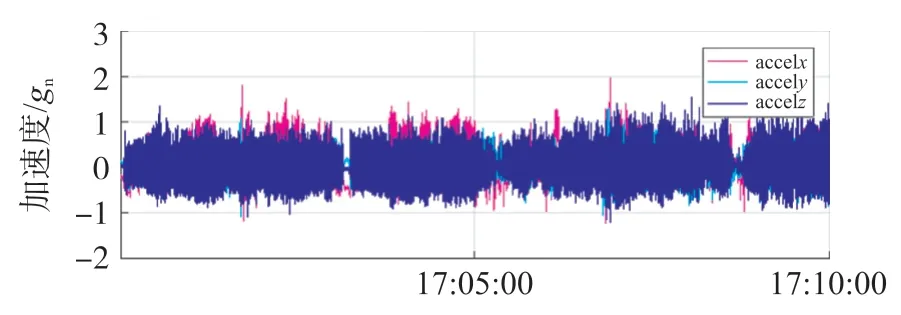
图4 三轴加速度曲线图

图5 所示是以时间为X轴,三轴角速度为Y轴的曲线图。

图5 三轴角速度曲线图

图6 所示是以时间为X轴,三轴磁向量为Y轴的曲线图。

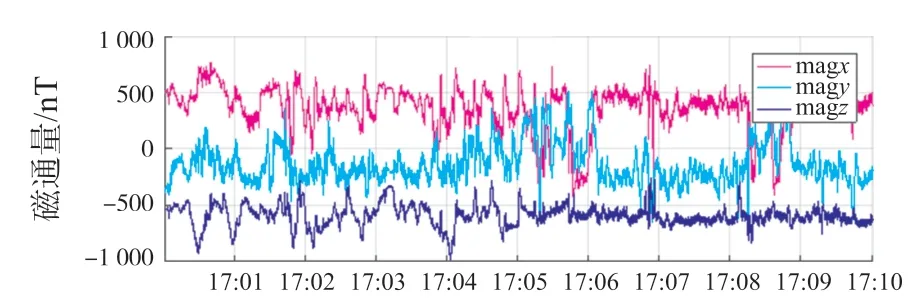
图6 三轴磁向量曲线图

图7 所示是以时间为X轴,分别以翻滚角(θ)、俯仰角(ψ)、航向角(γ)为Y轴的曲线图。

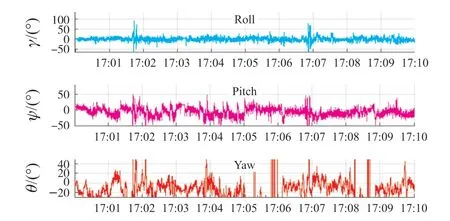
图7 姿态变换曲线图

对于姿态的变换,是将解算出来的俯仰角、翻滚角和航向角通过计算转换为在图上显示的点的变换。

首先计算航向角γ,即xOy平面中的转动,只需要让三角形的3 个点分别在下图中显示的大圆和小圆上即可。如图8 所示。

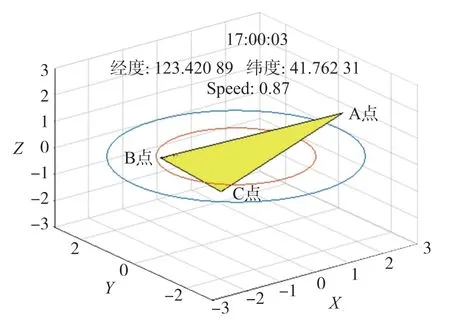
图8 姿态变换三维图

对于俯仰角ψ,规定以坐标(0,0,0)的点进行旋转,即2 个圆的圆心,因此计算俯仰角ψ需要在xOz平面内计算,通过公式sin(ψ)就可以计算出A、B、C3 个点分别在Z轴上的坐标,同时在A点变换后,其相对应的X轴、Y轴变换公式是cos(ψ)。

对于翻滚角θ,需要计算B点和C点分别在Z轴上的坐标,因为这个三角形是绕着(0,0,0)转的,并不是绕着BC的中点旋转,因而无法利用BC的长度乘以sin(θ)计算获得。所以需要通过圆心作一条直线和BC线平行,假设其与AC交与F点,与AB交与E点。如图9 所示。

图9 姿态变换计算三角形

无论ψ和θ如何转动,OF都是位于xOy平面内的,利用公式sin(θ)OF就可以得到F点在Z轴的变化,从而通过等比计算就可以得到C点在Z轴的变化,B点的变化和C点是一样的,只是方向相反,将BC的坐标在xOy平面利用公式cos(θ)得到,再进行缩放就可以得到三角形的三个坐标点。

6 结论

使用三轴加速度计、三轴陀螺仪、三轴磁力计采集姿态数据,采用统计均值法,进行九轴姿态数据校准,有效地解决了零点漂移,简单易行；采用互补滤波法,合理调整PI 参数,进行数据融合,较之卡尔曼滤波,计算量小,更适合工程实现；针对加速度计无法修正航向角的问题,采用加速度计修正磁力计的水平问题,再用磁力计修正航向角。弥补了六轴传感器无法修正航向角的不足,全方位修正了姿态角。经过实际车辆测试,能够真实地反映出汽车的运行状态。为监控汽车的运行状态提供了一种更简单、更实用的手段。