基于数据挖掘的含UPFC 输电线路纵差保护方案

范栋琛，宋亮亮，崔 玉，刘志仁，杨 毅，武 凯，李现军

(1.国网江苏省电力科学研究院,江苏 南京 210096；2.江苏省电力有限公司电力调度控制中心,江苏 南京 210096；3.国网江苏省电力有限公司无锡供电公司,江苏 无锡 214000；4.山东山大电力技术股份有限公司,山东 济南 250013)

随着全球能源互联网的建设,电网跨区域互联成为趋势,交直流混联系统扮演了重要角色,大型输电线路的保护成为了保护配置的关键[1]。目前为了对输电线路补偿有功和无功,统一潮流控制器(UPFC)也被广泛使用[2]。因此,含有UPFC 的输电线路纵联差动保护十分关键。

目前已有研究主要集中在输电线路纵联差动保护机制。李小鹏等[3]提出了一种基于反行波幅值比较的高压直流输电线路纵联保护方法。李刈等[4]提出了一种基于S 变换的高压直流输电线路纵联保护方法。索南加乐等[5]利用电流模型对输电线路纵联保护进行识别。杨亚宁等[6]提出了一种基于计算电阻的高压直流输电线路纵联保护方案。

还有部分文献研究了新技术在纵差保护中的应用。郭侨等[7]研究了光纤自愈网在线路纵差保护的应用。樊占峰等[8]针对特高压电网的纵差保护方案进行了研究。李静等[9]研究了三端纵联差动保护原理及在北京地区的应用。××等[10]分析了超导储能装置对输电线路纵联电流差动保护的影响。

但是目前研究含有UPFC 和风电场接入的输电线路纵差保护方案较少。尤其是当大容量的DG 接入到含多端电源的配网线路中形成T 接形式后,流入T 型线中纵差保护的电流相角和大小均发生了改变。系统正常运行及保护范围以外短路时,进到差动继电器的电流差值可能高于其整定值,引起误动。

为此,针对含有UPFC 和风电场的输电线路设计了基于数据挖掘的纵差保护方案。首先分析了数据挖掘的主要过程,针对Kalman 滤波以及决策树进行简要分析。然后说明了现阶段传统纵差保护出现的问题。提出了基于数据挖掘的线路纵差保护方案。最后利用仿真模型对所提模型的准确性进行了分析。

1 数据挖掘主要方法

1.1 数据挖掘流程

数据挖掘泛指对数据的综合处理、得到有效数据的过程,主要包括3 方面内容:

(1)数据预处理。数据预处理主要包括补全缺失数据和清理异常坏数据:对无可靠修改根据的数据,进行删除处理。经过数据预处理,可以获得完整的数据库。

(2)数据泛化处理。可以采用K-均值聚类算法对预处理后的数据进行泛化处理,得到泛化数据集。

(3)获取关联规则。一般采用决策树对泛化数据集进行关联规则分析。

流程图如图1 所示。

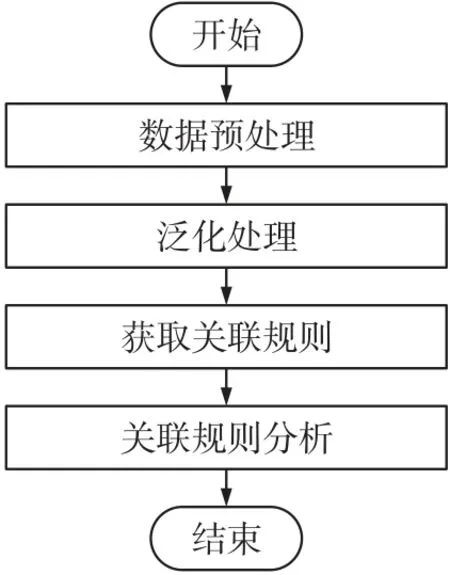
图1 数据挖掘分析流程图

1.2 Kalman 滤波

Kalman 算法能够利用前一时刻的估计值与当前时刻的测量值对系统变化的状态进行估计,并结合噪声和信号的时空模型,求解当前时刻的估计值,该过程使用最小均方误差作为估计准则,具有较高的可靠性。

该算法具有数值解的预估-校正能力,主要分为两个部分:时间更新过程、测量更新过程。一次时间更新和测量更新计算后,再次重复以上过程,上一时刻计算所得到的后验估计被作为下一次计算的先验估计,循环往复,逐渐接近回归对象,从而最终得到最优估计值。

1.3 决策树

决策树学习能够从无序的、无规则的案例中,抽象成决策树的形式对大数据进行分类,是一种以实力为基础的归纳手段,能够掌握数据在变化过程中的关键指标。其中应用最广泛的是ID3[11]算法。

设在训练集S中,由n个数据样本组成,且这些数据样本可分为m类,分别表示为Ci(i=1,2,…,m),对于每类Ci含有ni个样本,S划分为m个类的信息熵表示为:

式中:pi表示S中的样本属于第i类的概率。设属性A的取值为v的集合表示为Sv,则属性A的信息熵表示为:

式中:E(Sv)表示Sv中样本在实际的各个类别中的信息熵,则属性A相对S的信息增益表示为:

决策属性的信息增益进行排序后,选择最大的属性作为数据集S的决策属性节点,从属性点接出分支,再从剩余属性中选择信息增益最大值,重复上述过程,最终建立决策树。

2 基于数据挖掘的纵差保护机制

2.1 传统纵差保护存在的问题

传统纵差保护的依据是流入保护区域的电流之和为0。在含有容性充电电流的输电网中该规则可能不适用。尤其是统一UPFC 装设之后,电流纵差保护的整定值选取较为困难,尤其是UPFC 的控制参数易变化、故障下UPFC 运行模式不固定。再考虑到目前分布式电源的渗透率不断增高,风电仅考虑其有功注入,故障电流方向和大小都极易发生变化,使得传统纵差保护不适应新的电网发展态势。

目前针对T 接逆变型分布式电源系统中的纵联差动保护研究较多,表明线路两端差动电流大小与过渡电阻大小、系统两侧等值电势相角差和逆变电源接入容量均有关,这就增加了传统保护的难度。

2.2 基于数据挖掘的纵差保护方案

所提输电线路纵差保护方案示意如图2。变电站1 和2 通过500 kV 输电线路连接。线路两端均连接风电场和UPFC。根据故障时的电压电流序分量以及暂态时的不同相之间无功进行差动量的选择。

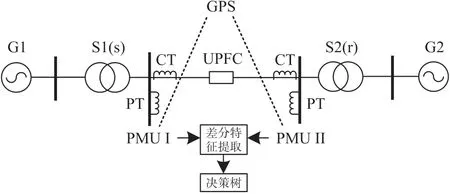
图2 基于数据挖掘的纵差保护示意图

选择基于Kalman 滤波的相量测量单元(PMU)进行相量估计并提取相应特征。Kalman 滤波算法详见文献[12]。一旦线路两端特征量根据Kalman滤波PMU 估计出,就开始计算线路差动量。

所提保护方法还需远距离通信通道实现电压电流测量量的交换并完成线路两端电压电流测量的同步。目前超高压、特高压主要利用光纤通信通道,三相电压和电流量可以高效地进行传输。因此,提出基于保护机制的通信平台。该平台能够利用卫星导航系统的精准对时,实现测量同步传输,确保保护信号的收发时间的准确度。

决策树是一种启发式学习方式。在一个周期内得到故障后差动量,构建决策树。所提方案包括21个可能的差动特征,具体包括:

其中,下标1,2,0 分别表示正序分量、负序分量和零序分量；s和r分别表示送端(站1)和受端(站2)。

基本的相量测量过程包括根据电压电流的基频进行序分量估计。首先,电压电流模拟量转换为数字量。然后,根据Kalman 滤波算法对基频分量进行估计。其中正序、负序、零序分量计算如下:

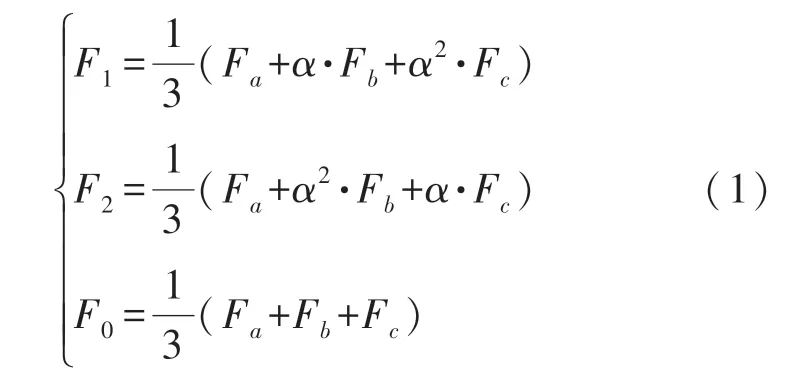
式中:F可以表示电压相量V,也可以表示电流相量I。α=1∠120°。

首先,线路两端电压电流同步采样量通过Kalman 滤波进行处理,得到电压、电流相量的估计值。然后利用该估计值,根据式(1)得到电压电流的序分量。最后,利用得到的相量、序分量计算X1-X21的差分量。

3 算例分析

3.1 仿真说明

选取两站系统进行仿真,搭建Simulink 模型,采样频率为1.2 kHz。决策树输入为含有21 个数据的单一故障向量。目标输出分类为0(无故障、区外故障)、1(a-地)、2(b-地)、3(c-地)、4(a-b)、5(bc)、6(c-a)、7(ab-地)、8(bc-地)、9(ca-地)和10(a-b-c)。

本文做出的假设如下:

(1)故障阻抗范围为0～100 Ω；

(2)故障距离考虑20%、50%、80%、95%；

(3)故障初始角为0°、30°、60°、90°；

(4)故障类型为单相接地、两相接地、三相短路；

(5)UPFC 电压相角θse为0°～360°之间；

(6)UPFC 串联电压注入量为正常电压的0%～15%；

(7)UPFC 的运行模式为自动潮流控制模式和旁路模式；

(8)风速为5 m/s、10 m/s、15 m/s。

仿真参数如表1 所示。

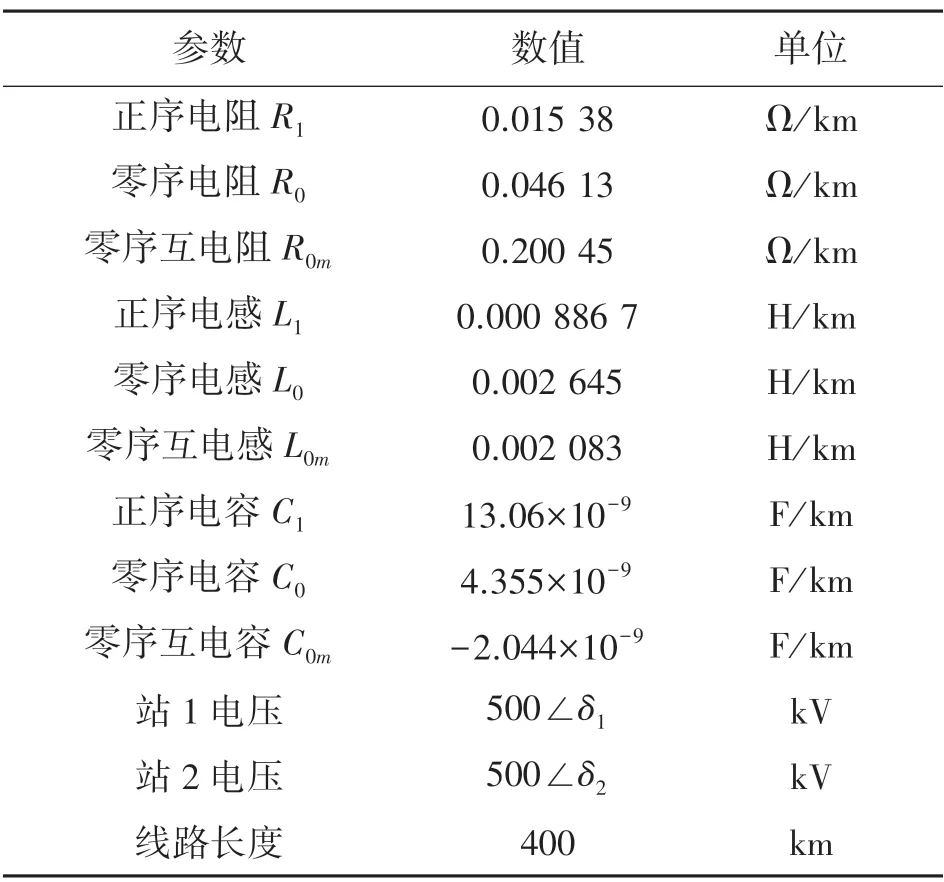
表1 IEEE 标准过电流保护特性常数

UPFC 安装于线路中部,UPFC 包括2 个48 脉冲的电压源逆变器,分别叫做静态同步补偿器和静态同步串联补偿器,通过2 个2 500 μF 的公共直流电容连接。

由40 个单台1.5 MW 组成的60 MW 风电场连接于站1 的位置。

利用构成的故障状态,训练决策树并对不同的数据集合进行测试。混淆矩阵如表2 所示,其中0表示无故障,表2 给出了给定数据集的实际故障和预测故障的对比信息,可以看出受训的决策树可以提供准确率为100%的故障分类。例如(70%～30%)数据集意味着混淆矩阵能够给出总数据30%的分类结果。考虑5(Rf)×4(故障初始角)×10(故障类型)×3(故障位置)×3(UPFC 电压值)×3(风速)＋100(区外故障)=5 500 种故障情况。

表2 混淆矩阵

3.2 算例分析

根据提出的决策树分析方法,得到故障分类结果如图3 所示。从图3 也可看出,UPFC 实际或最优的故障特征为X8,X10,X11,X12,X15,X19,X20,比最初输入的21 个特征要少。这也说明了决策树的选择能力。另外,决策树将故障分类为接地故障和不接地故障,分界点为X15,即零序电压。

图3 决策树结果

表3 给出了数据量增长后决策树分类的准确度。说明决策树的准确程度很高。可以看出,决策树求解的效率很高,耗时较少。通信延迟可能会影响响应时间,因此需要线路两侧时钟完全同步。

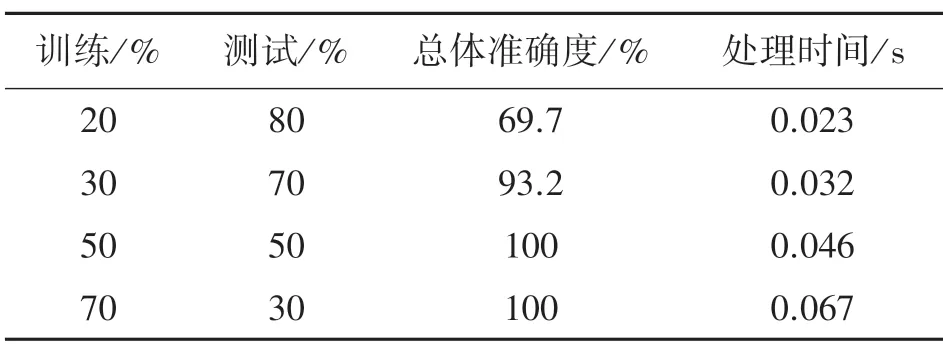
表3 决策树准确程度

为了说明所提方法的效果,将预测正确故障数与预测故障总数之比λ作为评判指标。

得到指标计算结果如表4。

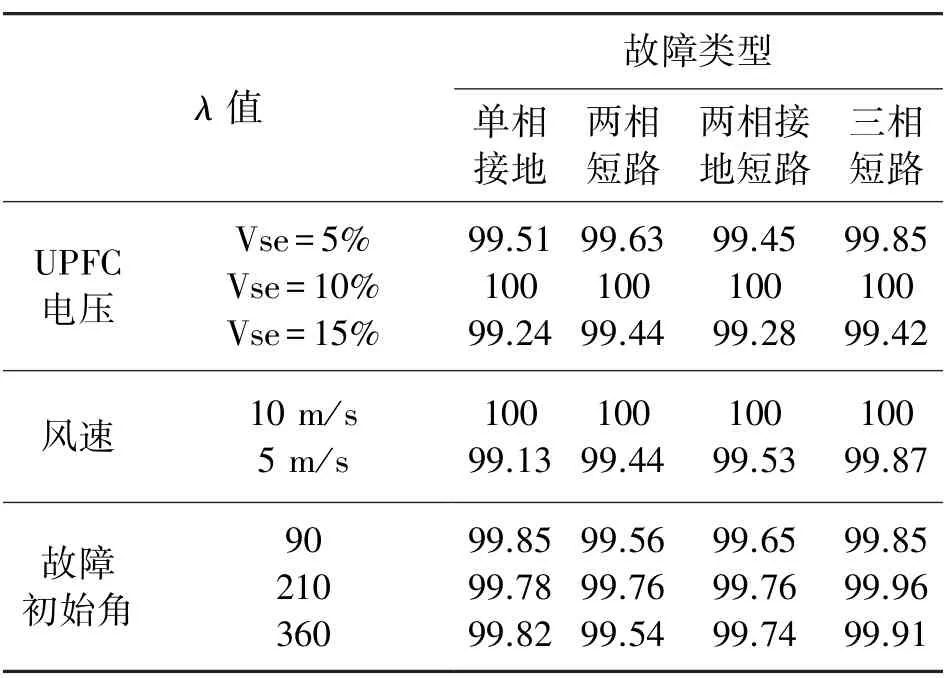
表4 λ 指标值

3.3 结果分析

通过上述分析可以看出,当故障发生的参数发生变化时,决策树的准确率也会发生变化,但是准确率都大于99%,说明在不同情境下,利用所提方法进行故障判断是十分有效的。

由于含UPFC 的线路纵联差动保护依靠线路两端的的保护元件,在分析不同故障的情况下,得到故障树,能够更加高效和准确地确定故障,实现故障的准确判断。

4 结论

提出了一种针对含有UPFC 和风电接入的输电线路纵差保护方案。首先利用Kalman 滤波对电压和电流量进行预处理,利用得到的差分特征构建最优决策树,从而实现故障状态的选择性。该方法在仿真模型中进行验证,在响应时间和响应准确度上有很高的可靠性,可以推广应用至大规模互联系统。