基于频域滤波的矿山微震信号分离方法研究

吴彦博，张 达，冀 虎，戴 锐，石雅倩

(1.矿冶科技集团有限公司，北京 102628；2.金属矿山智能开采技术北京市重点实验室，北京 102628；3.国家金属矿绿色开采国际联合研究中心，北京 102628)

我国经济快速发展导致金属、非金属等资源需求量日益增大，矿石开采量不断增加，逐步形成了大量的采空区。部分采空区能够依靠有效的充填、注浆等方法进行及时治理，然而仍然有大批采空区不能够被及时处理，地下采空区面积越来越大，从而导致地面塌陷、井下发生岩爆、冒顶、塌方等地压灾害，不仅对井下安全开采造成威胁，也对周边生态环境产生不可估量的破坏。微震监测技术能够利用井下岩体在挤压变形、破坏以及微裂隙产生过程中所发出的震动波来进行岩体分析和稳定性评估，是关键的地压监测技术之一。但在微震监测系统实际监测过程中，系统采集到的数据不仅包含岩体破裂的微震信号，还包含开采爆破、机械作业、人员活动、电干扰、凿岩信号等复杂震动信号，而且在传播过程中这些震动信号会在时域和频域上产生叠加，导致真正用于岩体稳定性评估的微震信号难以分辨，微震分析中的数据不准确，分析结果亦不可靠。

为了解决上述问题，首先要实现对震动信号开展时域及频域的分析，只有分离出有效震动信号才能够开展有效的波形识别，从而辨别出微震信号。现已有大量文献采用傅里叶频谱分析或小波分析等手段对矿山微震信号进行分析与识别，但仍存在通用性不足、计算方法复杂、计算量大等问题。本文研究了一种基于谱峰识别和频域滤波技术的矿山多源震动信号分离与提取有效方法，能够降低噪声干扰对矿山微震信号的影响，为进一步实现矿震信号的处理及分析提供新的思路。

1 基础理论

1.1 傅立叶变换及其反变换

傅里叶变换是目前信号频域分析最常用的方法之一，其能够将信号从时域转换到频域，进而从频域上得到很多在时域上不易发现的信号特征。快速傅立叶变换(fast fourier transform，FFT)是傅立叶变换中一种的高效算法，能够将时域信号转到复数域信号来快速完成频域转换。其中，复数域信号中的实数序列可以看做虚部为零的复数，例如某实数信号x(n)可认为是将实部加上数值为零的虚部，变成复信号y(n)=x(n)+j0，从而进行FFT计算。MATLAB提供的FFT工具函数可以实现任意点数的混合基运算，本文在实际应用研究中用C语言实现了混合基FFT算法，作为本文数据处理的软件工具。

1.2 窗函数

FFT对有限长的信号做频谱分析时，会产生频谱泄露现象，原本该频率的能量会泄漏到其他频率上，导致频谱不准确。当输入信号的频率不是FFT分辨率的整数倍时，信号的能量就会向整个频域扩散，此时原本幅度比较小频率就会叠加属于其他频率的泄露能量，使得原本小幅度的频率能量无法在频谱中显示其真实的信息。因此，需要建立窗函数与信号叠加，可以在一定程度上防止或减少能谱外泄效应。目前常见的窗函数有矩形窗、汉宁窗、海明窗、三角窗高斯窗等，具体根据实际数据和所要解决的问题而定。

由于窗函数同样会造成信号产生不同程度的失真，所以在选择和应用窗函数时，一方面要考虑窗谱本身的特性，另一方面还要考虑信号本身的特点。如果对频率分辨率要求较高，而谱幅值精度要求不高，可直接选用主瓣窄的矩形窗。在实际应用中也可以选择多种窗函数进行比较和选择。对于采集触发得到的微震信号，一般能量比较集中，而波形特征又不统一，所以很难选择一种固定的窗函数形式，为保证主频带能量尽量保留、其他频带能够快速压制，因此选用一种参数可设的凯泽窗(图1)，通过调整控制参数来修改窗的形态，从而达到不同的阻带衰减要求。其中，乘数因子可采用零阶第一类修正贝塞尔函数。

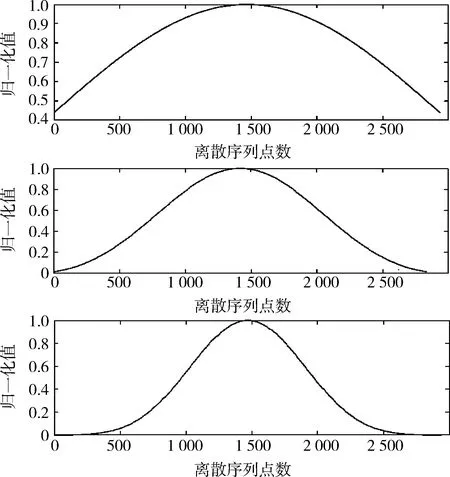
图1 凯泽窗Fig.1 Kaiser window

2 FFT频域滤波

通过FFT可以知道信号序列中包含的频率成分，以及各频率成分的振幅大小；反之通过快速傅立叶逆变换(inverse fast fourier transform，IFFT)，又可以将频域的信号变换到时域，从而得到与原来信号长度相同的时间序列。

2.1 FFT计算

输入实数序列信号数据如图2所示，经过FFT计算的结果为复数序列对称共轭形式，其对称实数域和共轭虚数域如图3所示。

图2 原始微震信号及能量频谱Fig.2 Primary seismic signal and energy spectrum

图3 对称实数域与共轭虚数域Fig.3 Symmetric real number domain andconjugate imaginary domain

为保证对频谱复数序列进行FFT反变换之后能够得到实数序列，需要保留频谱复数序列的共轭对称特性。以如图4所示的长度位为9的奇数频谱序列X1(0∶8)，和长度为10的偶数频谱序列X2(0∶9)为例。X1(0)和X2(0)部分代表直流分量，可直接保留不做处理。序列X1(1∶8)分作X1(1∶4)和X1(5∶8)两个部分，即这两个复数序列为共轭关系，实部相对称。序列X2(1∶9)分作X2(1∶4)和X2(6∶9)两个部分，这两个复数序列满足共轭关系，其中实部对称，X2(5)为对称中心直接保留即可。对满足以上条件的频谱序列进行FFT反变换，直接取其实部，即可得到滤波后的实数序列。

图4 奇数和偶数长度序列Fig.4 Odd & even length sequence

2.2 频域滤波

通过FFT可以在频域中对信号的部分频段做滤波处理，再通过IFFT得到时间序列信号。值得注意的是，在进行IFFT时需要将奈奎斯特频率之后对应的频点位置通过共轭对称的方法来补全，以得到正确的时域信号。因此整个滤波过程可以分解为五个步骤。

第一步：通过局部极值法获取谱峰频点，见式(1)。

S{xi}={xi|f(xi+1)≥

f(xi)}∩{xi|f(xi-1) ≤f(xi)}

(1)

第二步：过滤选取有效的频谱点。

方法一：在局部极值集合的基础上多次迭代，见式(2)。

S′{xi}={xi|S(xi+1)≥

S(xi)}∩{xi|S(xi-1)≤S(xi)}⟹

S″{xi}⟹…Sr{xi)}

(2)

通过多次迭代计算局部极值，得到最终需要的谱峰频点集合。迭代次数根据频谱特征来确定，迭代次数越多，获得的谱峰越少。如果信号频谱比较集中可以适当减少迭代次数，反之如果信号频谱比较复杂，则可适当提高迭代次数，目的是获得占主要成分的频带分量，并且考虑频域覆盖度。

方法二：以能量权重优先为原则，保留能量最大的频谱分量，见式(3)。

Sr{xi}={xi|f(xi)≥λ}

(3)

式中，λ为可调阈值，取值可以参考局部极值频点集合的3/4百分位数。方法二计算过程较为简单，但会损失一部分能量较小的频域分量，因此该方法更适用于频谱分布比较集中的信号。

第三步：选取合适的频谱分量带宽，取值标准可参考1/2峰值处带宽的2倍。在减少谱峰串扰的基础上带宽选取可以宽一些，以降低信号的能量损失。

第四步：获取分量并进行滤波处理，利用平顶窗函数加权计算。加权系数S(n)见式(4)。

(4)

式中：n为序号；N为信号长度，0≤n≤N-1。该过程可以提高信号的信噪比，同时会改善信号分量谱峰间串扰问题。

第五步：频域数据经过IFFT得到时域信号分量，完成信号的频域滤波过程完成。

3 信号滤波与信源提取实例分析

3.1 信号分量粗提取

以某矿山的微震和爆破两种实际信号为例进行说明。在对信号分量进行滤波提取之前，首先进行频段的划分和提取。图5和图6中的两个例子先不考虑信号的实际频谱特征，大致选取几个频段进行分量提取。图5为微震信号实例，分别选取100～400 Hz、200～400 Hz、400～600 Hz三个频段。其中，图5(a)为原始微震信号波形，图5(b)为0～200 Hz频段分量，图5(c)为200～400 Hz频段分量，图5(d)为400～600 Hz频段分量。图6为爆破信号实例，分别选取0～400 Hz和1 000～1 200 Hz两个频段。其中，图6(a)为原始爆破信号波形；图6(b)为100～400 Hz频段分量；图6(c)为1 000～1 200 Hz频段分量。

图5 微震信号实例Fig.5 Example for microseismic signal

图6 爆破信号实例Fig.6 Example for blasting signal

信号能够实现多源分离的关键因素是谱峰识别和带宽提取，识别有效的谱峰可以提高信号分量的识别能力，这也是信号多源分离的前提；合理提取带宽能够提高分量信号的还原度。分析表明，微震信号更偏向低频，能量时间分布周期较长，信源成分较单一和集中。

对比各信号分量与原始信号可以发现，图5(b)分量信号与原始信号尾波十分接近，图5(c)分量信号与微震主能量时段相吻合，而图5(d)分量则无明显的波形特征；图6(b)与爆破信号形态接近，图6(c)为爆破信号的高频部分，与原始信号相比无明显特征。通过以上两个信号分量粗提取的例子可以看到，提取的信号分量特征不明显，分量信号波形形态也比较随机，不能得到统一的分量数据，无法有效开展进一步的统计分析。

3.2 频谱细分

矿山现场的微震或爆破信号比较复杂，所以很难获得规律的一致性特征。在得到信号的频谱之后识别有效谱峰，认为每一个谱峰是一种信源分量，然后按照信号频谱的谱峰来进行频带划分，针对每个频带进行窄带滤波，从而提取出信号中的多种信源分量。频带划分见图7。

图7 微震信号细分频谱Fig.7 Subdivision spectrum for microseismic signal

3.3 信源分量提取

信源分量提取应遵守以下原则：①两个相邻的抖动谱峰需要合并为一个来提取；②谱峰带宽需要保留一部分延拓重叠数据；③使用合适的窗函数生成滤波系数，以降低信号分量失真度。如图8所示，由以上分解到的时域分量数据可以分析得到：①各个分量时域信号触发特征明显；②触发到时数据一致性；③低频分量的振幅相对高频偏大；④能量频谱分布和时域分量趋势一致，振幅、能量较大的频段信号量对应的能量谱值也比较大；⑤各个分量的触发到时可以为原始完整信号的触发到时提供评估基础。

图8 多频带细分信号分量Fig.8 Multiband subdivision of signal components

4 结 语

本文通过FFT频谱分析和频域滤波，提出了一种矿山微震多源信号的实际可行的分析与分解方法。本方法以多源信号的谱峰分布为依据，进行信源成分识别，利用FFT窄带滤波有效实现了信源分量的分离与提取。通过实际数据分析实验结果表明，在信号源成分未知的情况下能够灵活有效实现了信号的多源分离，得到信源分量波形。信源分量的触发到时与原始信号的一致性，也从另一个角度印证了该方法的有效性。该方法为微震信号的分类识别、触发到时评估、能量震级的评估以及进一步的信号特征关联分析和样本库统计提供了合理有效的数据基础和技术支持，对矿山微震监测领域的信号分析提供了新的思路。