基于VSC整流站的模型预测控制器

夏 天，余 瑜，杨文康

（湖北工业大学 太阳能高效利用湖北省协同创新中心，武汉 430068）

引言

电压源换流器高压直流输电（VSC‐HVDC）采用可关断型电力电子器件和脉宽调制技术（PWM），它既可以对VSC‐HVDC系统传输的有功、无功功率实现独立控制，又可以在无源逆变方式下工作，实现向无源网络供电，从而克服了传统HVDC无法向无源网络供电的根本缺陷[1‐3]。而基于VSC‐HVDC的整流站一般采用双闭环PⅠ控制，该系统一般使用4个PⅠ调节器，这种控制方法需要整定大量的PⅠ参数，PⅠ参数整定困难，且调节参数的过程中存在复杂的解耦过程。

向无源网络供电的VSC‐HVDC控制策略是当前的一个研究热点[4]，文献[5]实现了对d轴电流和q轴电流的解耦控制，但没有对电压外环进行控制，并且控制精度不高。文献[6]建立了VSC‐HVDC系统的稳态数学模型，并基于此设计了相应的控制策略。文献[7]提出变流器电流内环电压外环的双闭环控制策略，但内外环响应速度差别较大，导致系统在出现故障时电压质量会降低。文献[8‐10]详细讨论了VSC‐HVDC向无源网络供电的相关控制策略，并且通过仿真验证了在向无源网络供电方面VSC‐HVDC具有很大优势。

本文针对以上不足，对VSC‐HVDC系统中的整流站进行理论分析，并分析在传统双闭环PⅠ控制下的VSC‐HVDC整流站的有功功率、无功功率。通过引入模型预测控制，提出了一种基于VSC‐HVDC整流侧的有功、无功功率控制器。功率控制器结构简单，解决了传统双闭环PⅠ控制器内环和外环的PⅠ参数众多且难以整定、控制系统难以实现多目标优化等问题，最后通过MATLAB仿真平台对VSC‐HVDC整流侧模型建模，分析VSC‐HVDC整流站在传统双闭环PⅠ控制和模型预测控制下的有功功率、无功功率和波形质量，以验证所提出控制策略的正确性和可行性。

1 VSC整流站数学模型

图1给出了VSC‐HVDC系统结构图，该系统由交流电源、整流器、逆变器以及整流侧、逆变侧各等效电阻、等效电感组成。为保持VSC‐HVDC系统输出功率稳定和输电系统的安全运行，整流侧主要功能是维持有功功率、无功功率稳定。

图1 VSC‐HVDC系统结构图

传统的双闭环PⅠ控制系统整流站控制策略为双闭环PⅠ控制策略，控制原理如图2所示。

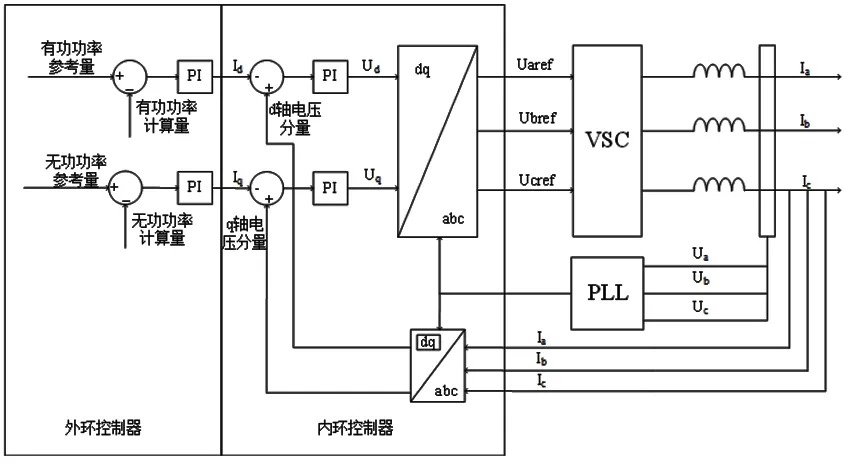
图2 双闭环PⅠ控制原理图

从图2可见，整个整流侧控制器由内环电流控制器、外环电压控制器、锁相环同步环节和触发脉冲生成等环节组成。内环电流控制器控制对象为外环控制器输出的交流侧电流I在d轴上的分量Id和q轴上的分量Iq，控制其波形和相位，以快速跟踪参考电流。而外环电压控制器则是根据柔性直流系统提供的交流侧电压，通过计算得出有功功率、无功功率的计算值，与有功功率、无功功率的参考值比较，再经过PⅠ环节输出为Id和Iq。锁相环节输出的相位信号用于提供电压矢量定向控制和触发脉冲生成所需的基准相位。脉冲触发生成环节是根据PWM原理，利用电流环输出的参考电压和同步相位信号产生换流器各桥臂的触发脉冲。

传统的VSC整流站采用电压外环和电流内环的双闭环PⅠ控制结构，整个控制环节有4个PⅠ部分，存在大量的PⅠ参数，在整定时需要通过大量的仿真来确定PⅠ参数，耗时长且过程复杂。同时，传统双闭环PⅠ控制策略需要对受电路参数影响的前馈补偿项进行解耦控制，且难以实现对控制目标的优化控制。为了克服传统控制策略的不足，本研究提出了一种基于VSC整流侧的模型预测功率控制策略。

2 VSC‐HVDC整流站数学模型

图3为向无源网络供电的VSC‐HVDC整流站拓扑结构图，图中Ea、Eb、Ec分别为整流侧三相电压，i为交流侧三相电流，R为整流站等效电阻，L为整流站等效电感，Cd为直流电容，idc为整流侧直流电流，Udc为整流侧直流电压。

按照图3所示电流方向，由基尔霍夫电压定律，可以得出整流侧在三相静止坐标系下的数学模型[11]：

图3 向无源网络供电的VSC整流站拓扑结构

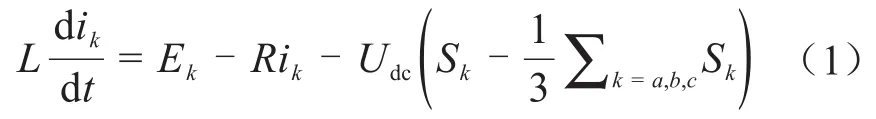
式中：k=a,b,c；开关函数Sk表示整流器每一相桥臂的开关状态，定义如下：

三相静止坐标系下的数学模型式虽然清晰地表示出了各物理量之间的数学关系，但仍存在着电气量方程组比较复杂的问题，影响控制器的设计，因此建立VSC整流侧在α,β两相静止坐标系下的数学模型，以此来简化三相静止坐标系下的数学模型。三相静止坐标系到α,β两相静止坐标系的转换矩阵如下：

因此式（1）可以表示为：

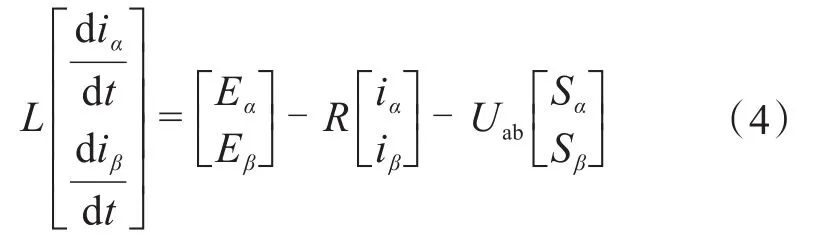
采用一阶向前差分法将式（4）离散化可以得到整流侧在α,β两相静止坐标系下的离散化数学模型：

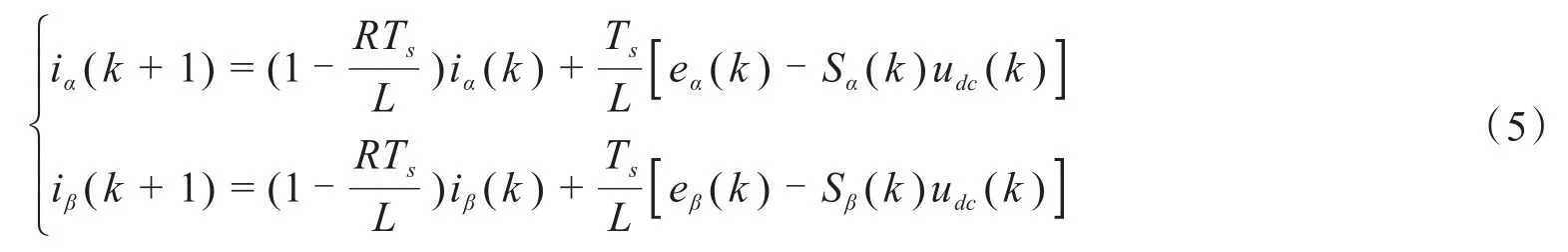
式中，Ts为采样周期，iα(k+1)、iβ(k+1)分别为α，β坐标系下电流在第k+1时刻的α轴分量和β轴分量，eα（k）、eβ（k）和udc（k）分别为交流电源的α轴分量、β轴分量和直流电源在第k时刻的值。由式（5）可以看出，通过对整流侧在第k时刻的电流采样值，可以准确地预知整流侧在第k+1时刻的电流值，因此能够准确快速地实现对整流侧电流的跟踪控制，提高整流侧对VSC‐HVDC系统故障扰动的抵抗力。

三相桥臂有8种可能的开关状态，则式（5）中对应的S（k）有7种可能的状态，见表1。

表1 开关状态与开关函数对应表

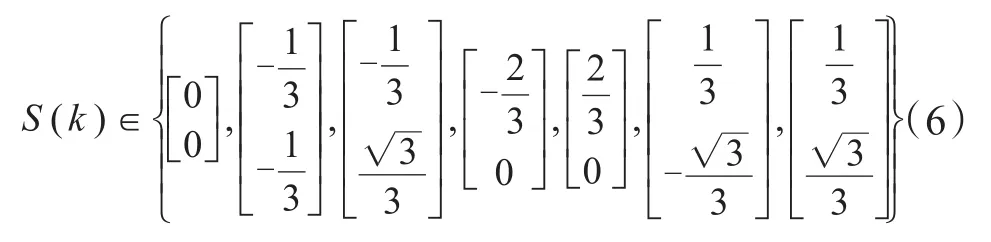
3 模型预测控制设计

VSC‐HVDC整流侧的首要控制目的是维持系统的有功功率、无功功率稳定，实现系统的安全稳定运行。其控制原理是根据有功功率、无功功率的参考值和整流侧输入电压电流等信息，确定整流站各桥臂的开关函数值，即桥臂的开关状态，进而控制整流侧输出的有功功率、无功功率。

3.1 模型预测控制函数

模型预测控制具有建模直观、动态性能好等特点，近年来在电力电子领域获得了广泛的应用研究[12]。根据瞬时功率理论，整流侧的有功功率和无功功率可以表示如下：

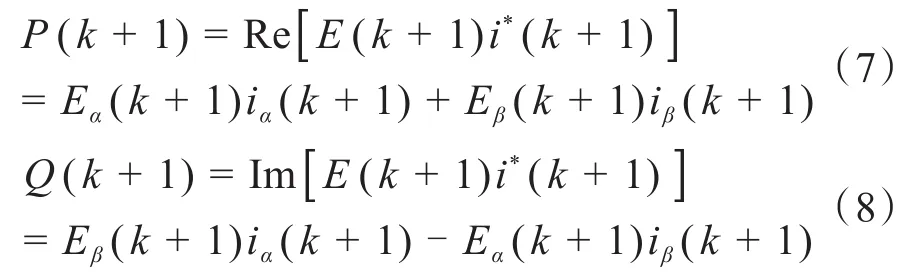
因为采样频率远高于电网频率则E（k+1）≈E（k），故式（8）可表示为：

将式（5）代入式（9），经过化简可得出以下公式：

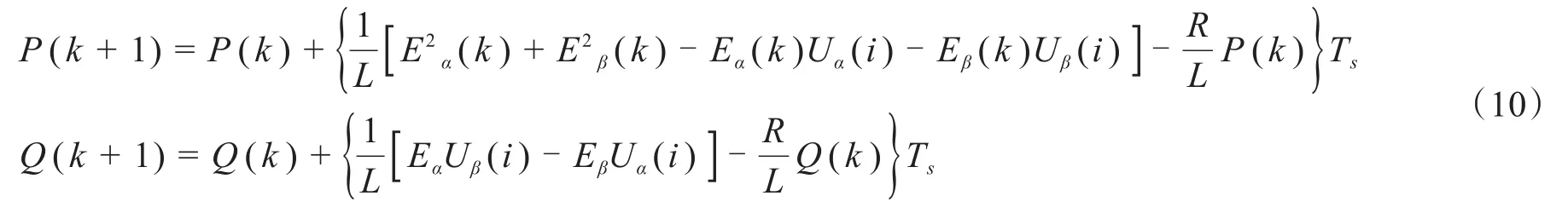
基于VSC整流侧的模型预测功率控制是一种基于模型的闭环优化控制方法。根据整流器k时刻出的开关状态组合（Sa、Sb和Sc）以及所对应的电流i，通过式（9）所示的VSC有功功率、无功功率预测模型进行计算，得到下一时刻VSC有功功率、无功功率所有的可能预测值。有功功率、无功功率的参考值与k+1时刻的有功功率、无功功率计算值通过式（12）所示的目标函数进行比较，选择目标函数最小的电流所对应的开关组合作为触发脉冲信号输入到VSC中，实现对VSC输出功率的最优控制。

3.2 构建目标函数

基于VSC整流站的模型预测控制器的控制目的为维持有功功率、无功功率与参考值接近且保持稳定，则可以构建以下目标函数：

式中，ω1、ω2为权重系数，Pref、Qref分别为有功功率参考值和无功功率参考值。

3.3 模型预测控制算法

图4为VSC模型预测功率控制策略原理图，由图4可知模型预测控制算法首先需要对k时刻的相关电气量（整流侧三相交流电压Eabc，三相交流电流i，直流电压Udc）进行测量；其次根据模型预测式（10）计算得到k+1时刻的电流预测值，根据目标函数（12）对有功功率、无功功率进行遍历计算，并与有功功率、无功功率参考值比较，得到最小目标函数对应的开关状态，输出到整流器中。图5为模型预测控制流程图。

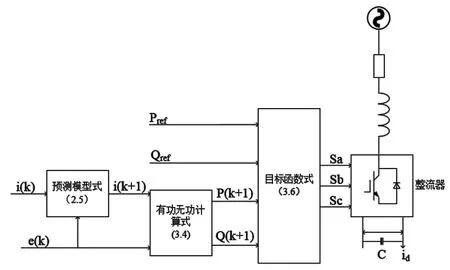
图4 VSC模型预测功率控制策略

图5 模型预测控制流程图

4 仿真结果与分析

为验证本文所提出的控制策略的有效性，在Matlab平台中搭建了图3所示的向无源网络供电的VSC‐HVDC整流站仿真模型，采用第2章提出的控制策略，设计需求为要保持系统的有功功率和无功功率分别在13 MW和6 Mvar。系统的仿真参数为：整流侧交流电源为25 kV，等效电阻R为0.6 Ω，等效电感L为0.053 H，直流侧电容为0.01 F，直流侧额定电压Udc为60 kV。

4.1 双闭环PⅠ控制

图6为双闭环PⅠ控制下的有功功率。由图6可以得出VSC整流站的有功功率在传统双闭环PⅠ控制下达到稳态的时间tp1≈0.022 s，整个系统输出的有功功率为13 MW，达到了设计中有功功率的要求；图7双闭环PⅠ控制下的无功功率，由图7可以得出VSC整流站的无功功率在传统双闭环PⅠ控制下达到稳态时间tq1≈0.023 s，整个系统输出的无功功率为6 Mvar，达到了设计中无功功率的要求；图8为双闭环PⅠ控制下的交流电流THD，由图8可以得出VSC整流站交流电流的谐波畸变率H1=5.06%，波形质量一般，波形中存在一定量的谐波。

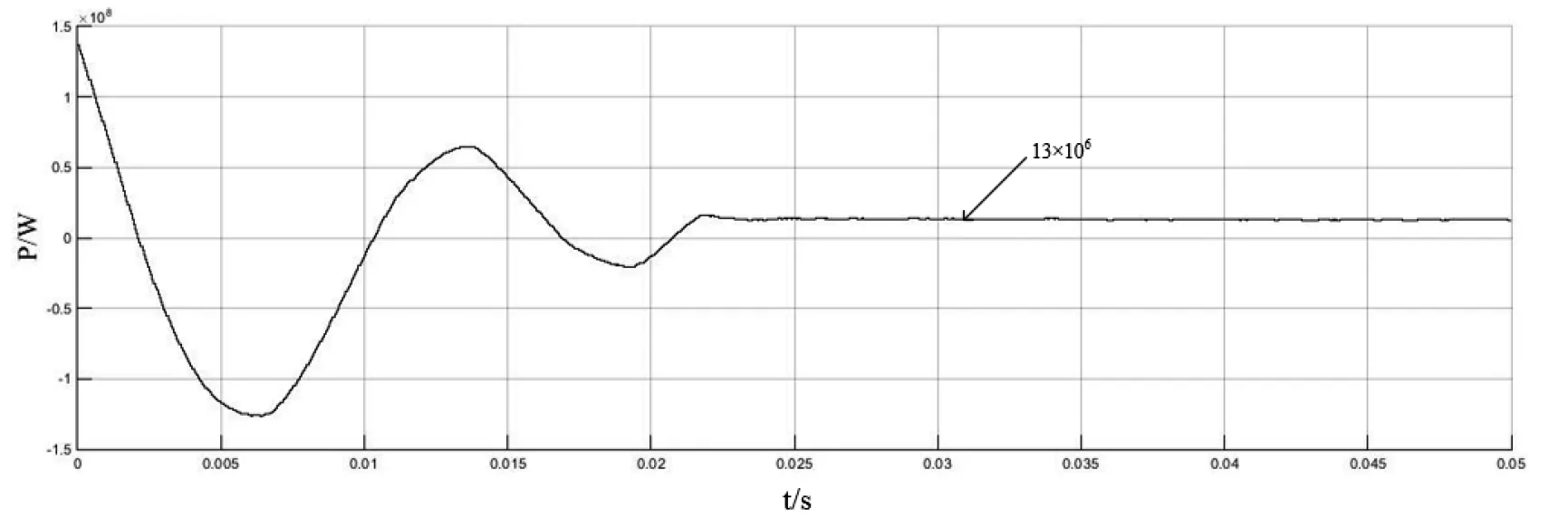
图6 双闭环PⅠ控制下的有功功率

图7 双闭环PⅠ控制下的无功功率

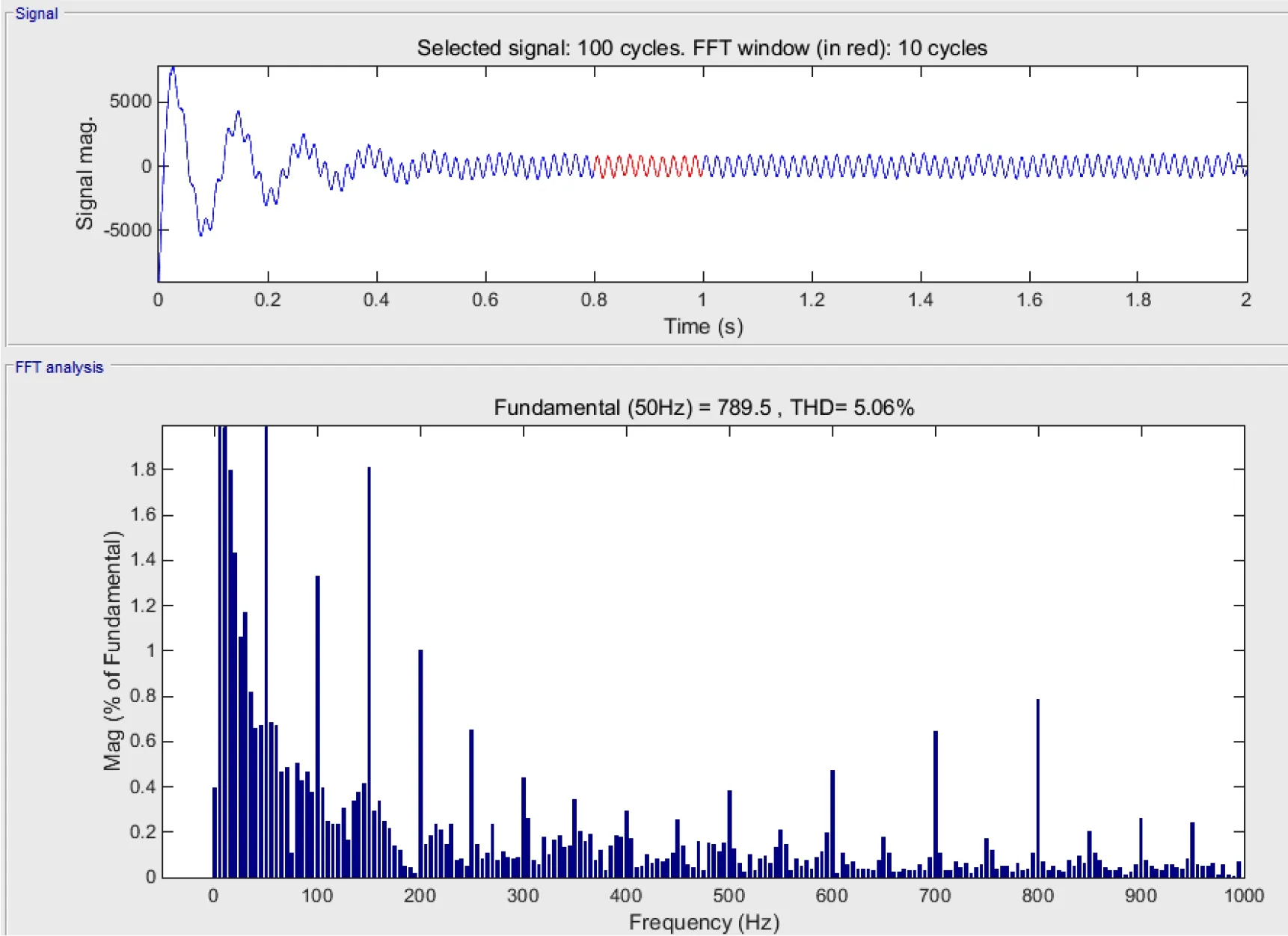
图8 双闭环PⅠ控制下交流电流THD

4.2 模型预测控制

图9为VSC模型预测控制（MPC）运行后的波形图。由图9可以得出VSC整流站的有功功率在模型预测功率控制下达到稳态的时间为tp2≈0.013 s，整个系统输出的有功功率为13 MW，达到了设计中有功功率的要求；图10为MPC无功功率波形图，由图10可以得出VSC整流站的无功功率在模型预测功率控制达到稳态的时间为tq2≈0.017 s，整个系统输出的无功功率为6 Mvar，达到了设计中无功功率的要求；图11为MPC交流电流THD，由图11可以得出VSC整流站在模型预测功率控制下的交流电流谐波畸变率H2=0.68%，波形质量相对良好，达到了设计的要求，证明该系统的稳定性和可行性。

图9 MPC有功功率波形图

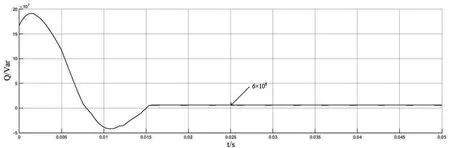
图10 MPC无功功率波形图

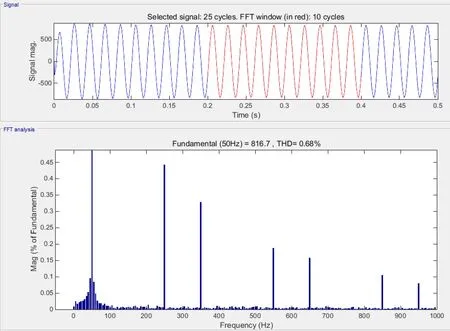
图11 模型预测功率控制下交流电流THD

VSC整流站的有功功率在双闭环PⅠ控制下达到稳态的时间为tp1≈0.022 s，在模型预测功率控制下达到稳态的时间为tp2≈0.013 s；VSC整流站的无功功率在传统双闭环PⅠ控制下达到稳态时间tq1≈0.023 s，在模型预测功率控制达到稳态的时间为tq2≈0.017 s；VSC整流站在传统双闭环PⅠ控制交流电流的谐波畸变率H1=5.06%，在模型预测功率控制下的交流电流谐波畸变率H2=0.68%。对比以上3项数据可以得出模型预测功率控制器在系统达到稳态时间、波形质量上都有明显的优势，因此可以证明本文提出的基于VSC‐HVDC模型预测功率控制的策略的可行性和正确性。

5 结论

提出的基于VSC整流站模型预测功率控制策略无需繁琐的PⅠ参数整定，省略了电流内环控制、电压外环控制，动态性能良好。在Matlab中搭建了向无源网络供电的VSC‐HVDC整流侧仿真模型，仿真结果表明，基于VSC‐HVDC的模型预测功率控制策略具有良好的动态性能。