双三相永磁同步电机无差拍电流预测控制

陈瑞成，夏 帅，乐子涛

（1.中国矿业大学徐海学院，江苏徐州 221000；2.中国矿业大学，江苏徐州 221000）

引言

相较于传统三相电机，双三相永磁同步电机具有低压大功率输出、低转矩脉动、适于容错运行等诸多优势[1]。但双三相永磁同步电机谐波阻抗较小，在使用电压源型逆变器供电时，会产生幅值较大的5、7次谐波电流，若不采取有效措施，必然导致定子损耗增加，加剧电机发热并影响输出效率[2]。同时，更高的自由度也意味着更复杂的控制策略。针对双三相永磁同步电机控制系统，国内外学者进行了广泛研究。文献[3,4]提出全维电流控制的概念，采用PⅠ调节器对谐波子平面的电流进行闭环控制，但由于谐波电流为交流量，PⅠ调节器对其跟踪效果差。文献[5,6]采用准PR控制器对谐波电流进行控制，显著降低谐波畸变率，但由于基波平面采用PⅠ控制，系统动态相应速度较慢。因此，对于双三相永磁同步电机控制理论的研究虽然已经取得了多方位的进展，但考虑多目标优化的控制策略仍然是目前研究的热点。

本研究在双三相永磁同步电机四维电流PⅠ控制的基础上，提出一种基于无差拍的双三相永磁同步电机电流预测控制策略。鉴于双三相永磁同步电机在空间解耦下的数学模型，基波平面和谐波平面互不干涉，分别在基波平面上引入无差拍控制器，用以提高系统动态响应速度；在谐波平面引入PR调节器，用以抑制谐波电流，并在仿真和试验中验证该方法的有效性。

1 基于无差拍的双三相永磁同步电机电流预测控制模型

双三相永磁同步电机系统具有高阶、强耦合、多变量、非线性的特点。因此，有必要通过适当的空间变换来建立新的降阶解耦模型，便于各种高性能控制算法在双三相电机驱动系统的实现。依据矢量空间解耦理论[7]建模，将各变量投影到基波空间以及各个谐波子空间中，可以得到在同步旋转坐标系下的数学模型。

双三相永磁同步电机的电压方程为：

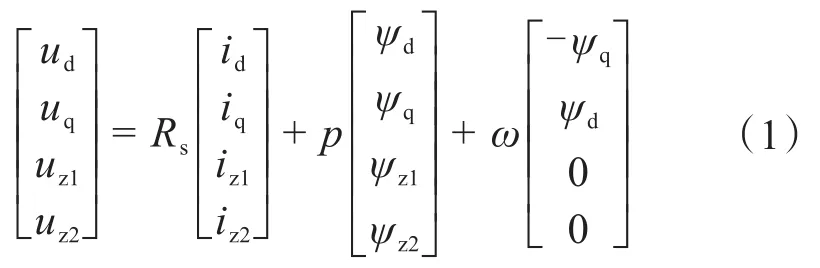
式中：ud和uq为基波平面电压分量；uz1和uz2为谐波平面电压分量；id和iq为基波平面电流分量；iz1和iz2为谐波平面电流分量；Rs为定子电阻；ψd和ψq为基波平面磁链分量；ψz1和ψz2为谐波平面磁链分量；ω为转子电角速度；p为微分算子。

双三相永磁同步电机的磁链方程为：

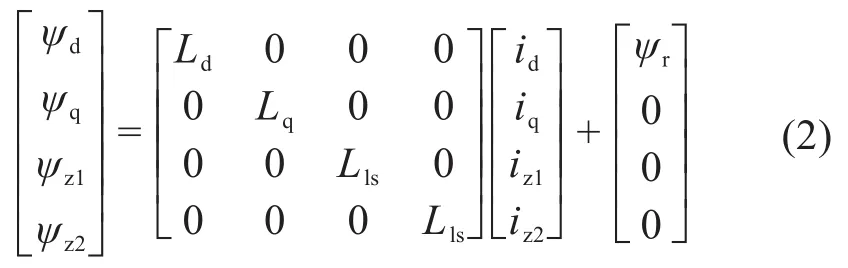
式中：Ld和Lq为基波平面定子电感分量；Lls为定子漏感；ψr为转子磁链。

根据双三相永磁同步电机空间矢量解耦下的数学模型，采用矢量控制方法进行闭环控制。图1为基于PⅠ调节器的传统四维电流矢量控制框图，d‐q基波平面采用转速电流双闭环控制策略，q轴电流给定值为转速外环输出，d轴电流给定值为0。z1‐z2谐波平面采用PⅠ调节器进行谐波电流抑制。

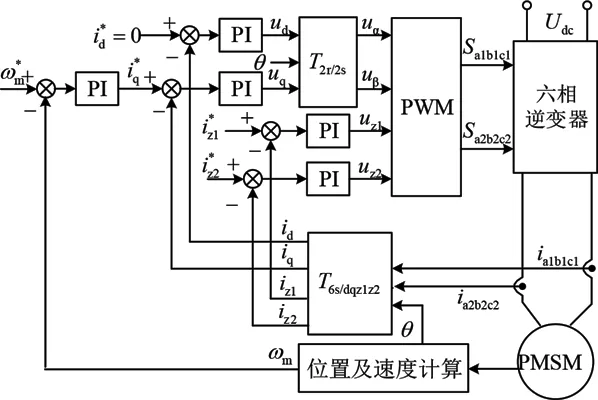
图1 双三相永磁同步电机四维电流矢量控制结构

为提高系统动态响应速度，采用无差拍预测控制器代替d‐q基波平面电流内环的PⅠ调节器。无差拍预测控制也被称为PWM预测控制[8]，指消除系统未来时刻的状态变量与参考信号误差为控制目标，选取最佳控制量满足对未来时刻动作方式的控制方法。

以定子电流作为状态变量，在采样周期Ts较小时，根据一阶欧拉离散，结合式（1，2）可得k+1时刻的d、q电流预测模型为：

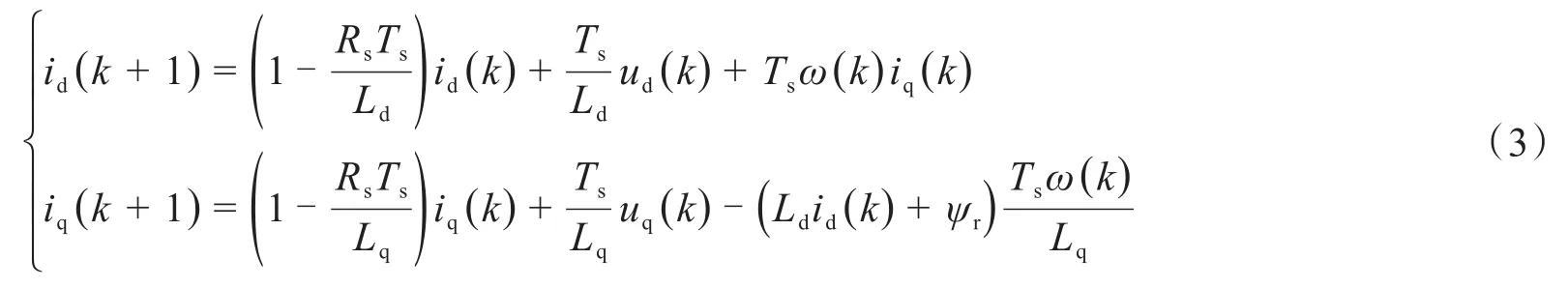
式中，k为离散化时刻。

由于采样时间很短，可将电流给定值近似等价于k+1时刻期望电流，则有：

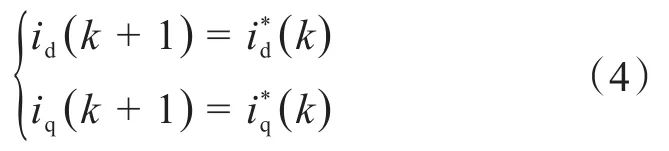
将式（4）代入式（3），并将k时刻电流预测值与k+1时刻电流预测值做近似处理，则无差拍预测控制器输出定子电压矢量为：

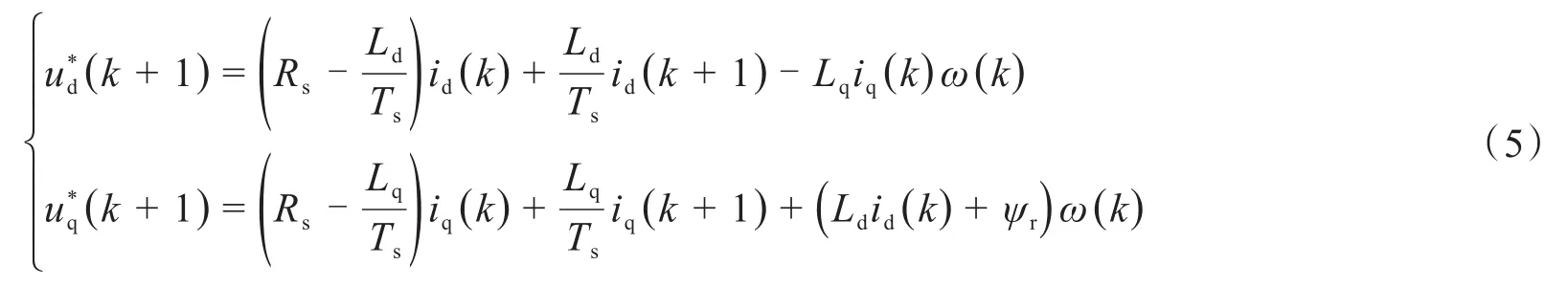
实际工程中，作用于电机上的电压幅值受到逆变器直流母线电压制约，为确保电机正常运行，避免d、q轴电压预测值超出允许的最大电压，通常需要作如下限幅处理：

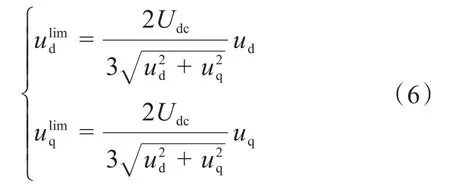
在当前k时刻对电流采样，将电流实际值与给定值进行比较，二者之间通常会存在一定偏差，为了补偿该误差，需要在k+1时刻使逆变器输出特定的d、q轴期望电压，以产生给定电流。由式（5）可知，期望电压的计算，必须先获得k时刻d、q轴电流的采样值与给定值，再经过SVPWM调制输出期望电压。理想状态下，k+1时刻输出的电流实际值即为电流给定值，使输出电流无差拍跟随电流给定值。

双三相永磁同步电机无差拍电流预测控制的控制系统框图如图2所示。从图2可以看出，与传统矢量控制相比，基波平面电流内环的传统PⅠ控制改为无差拍电流预测控制，可将控制误差在短暂的时间内强制为零，从而产生快速瞬态响应并减少转矩谐波。同时，为了更好地抑制谐波电流，用PR调节器代替PⅠ调节器，实现谐波平面电流控制。

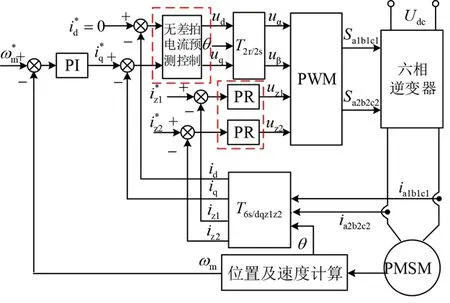
图2 双三相永磁同步电机无差拍电流预测控制结构

2 仿真与试验结果

针对本文提出的双三相永磁同步电机无差拍预测控制算法，进行了仿真和试验验证。仿真软件采用MATLAB/Simulink。直流侧电压为96 V，开关频率为10 kHz，电机参数如表1所示。

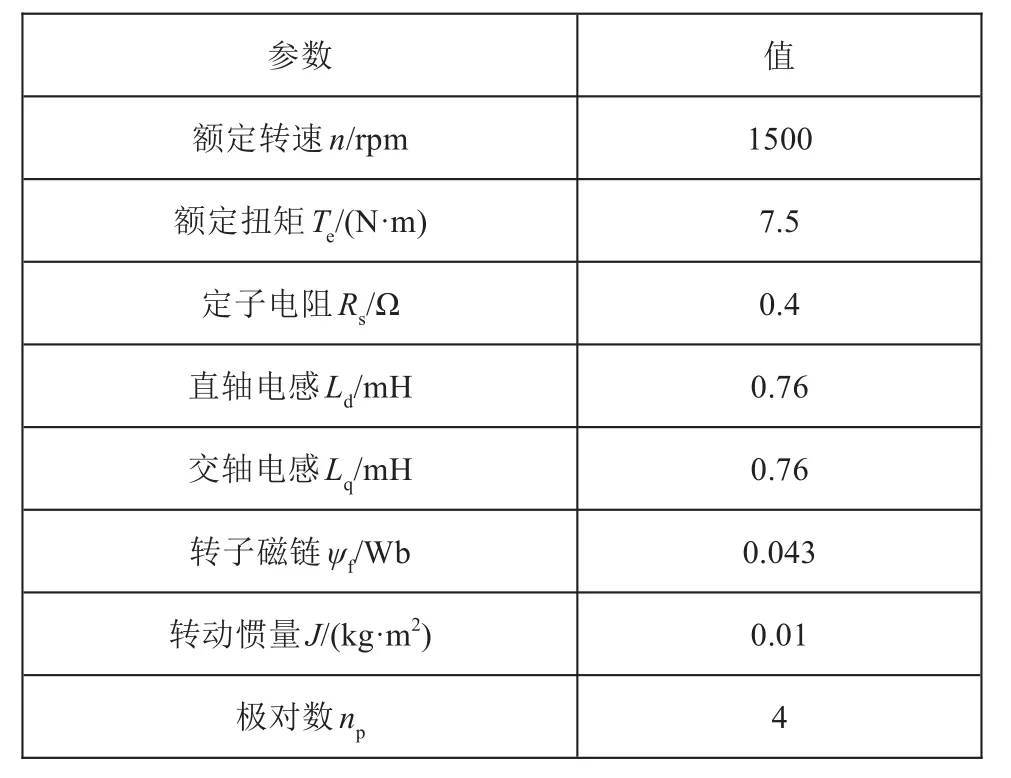
表1 表贴式双三相永磁同步电机参数

2.1 仿真结果

电机转速给定为1500 rpm，负载扭矩为7.5 N·m，分别对四维电流矢量控制和无差拍预测控制两种方法进行仿真。

图3为两种控制方法对应转速仿真波形，图3(a)为传统四维电流矢量控制对应转速波形，图3(b)为无差拍电流预测控制对应转速波形。从图中可以看出，传统方法的转速响应时间为0.245 s，改进后的算法转速响应时间为0.23 s，仿真证明了改进后的控制方法动态响应速度更快。

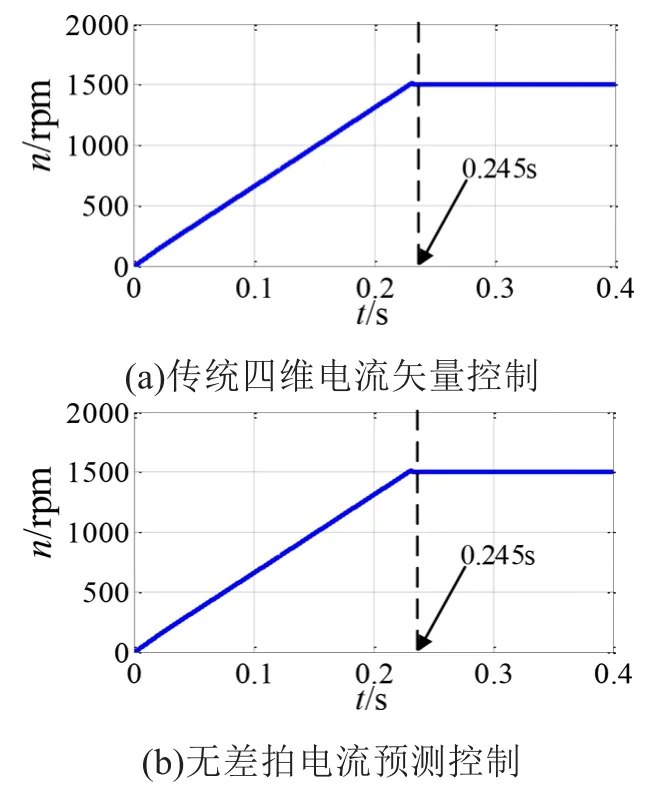
图3 两种控制方法对应转速仿真波形

图4为系统稳定后两种控制方法对应谐波电流iz1和iz2仿真波形，图4(a)为传统四维电流矢量控制对应谐波电流波形，图4(b)为无差拍电流预测控制对应谐波电流波形。从图中可以看出，采用改进后的算法使得电机谐波电流降低，仿真证明了改进后的控制方法谐波电流抑制效果更优。

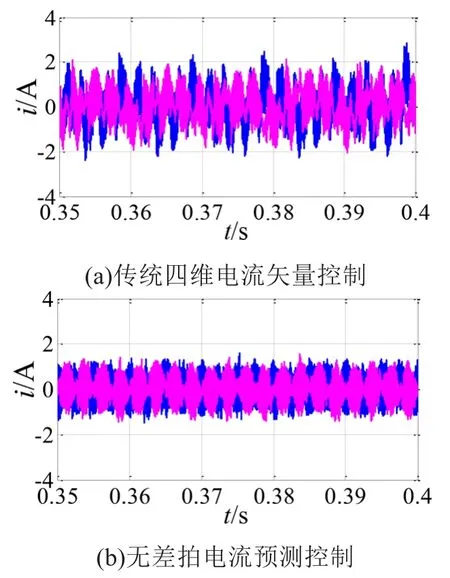
图4 两种控制方法对应谐波电流仿真波形

2.2 试验结果

对所提出方法进行试验验证，试验所用电源及电机参数和仿真参数基本一致，唯一的区别在于实际系统转动惯量更大。

图5为两种控制方法对应转速试验波形，图5(a)为传统四维电流矢量控制对应转速波形，图5(b)为无差拍电流预测控制对应转速波形。从图中可以看出，传统方法的转速响应时间为1 s，改进后的算法转速响应时间为0.92 s，试验证明改进后的控制方法动态响应速度更快。

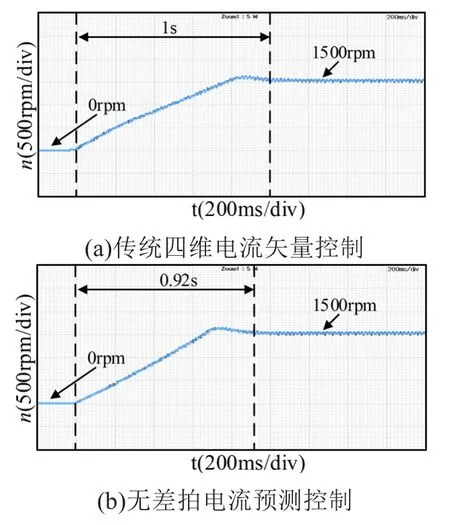
图5 两种控制方法对应转速试验波形

图6为系统稳定后两种控制方法对应谐波电流iz1和iz2试验波形，图6(a)为传统四维电流矢量控制对应谐波电流波形，图6(b)为无差拍电流预测控制对应谐波电流波形。从图中可以看出，采用改进后的算法使电机谐波电流降低，证明改进后的控制方法谐波电流抑制效果更优。

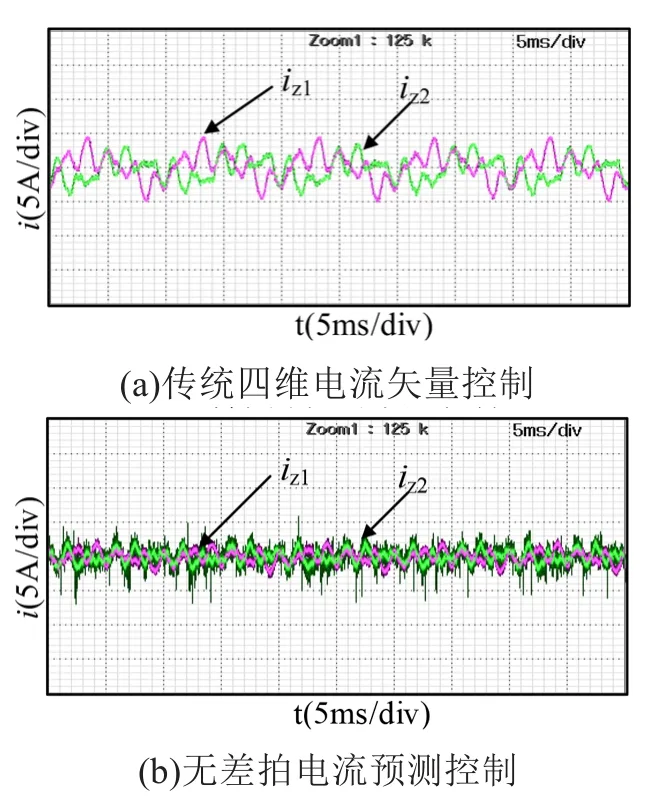
图6 两种控制方法对应谐波电流试验波形

3 结论

为了解决双三相永磁同步电机传统四维电流矢量控制的响应速度和谐波电流问题，提出一种基于无差拍的双三相永磁同步电机电流预测控制算法，在基波平面引入无差拍控制器，在谐波平面引入PR调节器，并进行了控制模型的推导和建立。仿真和试验结果表明，所提出的方案可以提高系统动态响应速度，具有较好的谐波电流抑制效果。本研究成果为双三相永磁同步电机的控制系统的设计提供了一个思路。