基于图像技术的输电线路覆冰厚度测量模型

闫 海

（三峡大学电气与新能源学院，湖北宜昌 443002）

引言

随着国民经济的快速发展，用电需求不断地增大，经济社会对电网运行的可靠性提出更高要求。输电线路作为电力系统的重要组成部分，起着运输分配电能、传递能量的关键作用，它的安全稳定运行关系着各地域供电的可靠性，维系着国民经济的发展[1‐3]。我国地域辽阔，地形复杂，输电网架分布广泛、运行条件十分复杂，而且长年暴露在野外，很容易受到气候、地势地貌、空气环流及冷暖空气对流等因素影响造成输电线路覆冰、舞动等事故。其中输电线路覆冰是很常见的现象，世界各地因线路覆冰过负荷时常发生输电线路断线、倒杆（塔）断线及线路舞动的电气事故，直接威胁人民的生产生活，同时对大型生产企业和电力系统造成巨大损失[4,5]。

文献[6,7]通过在杆塔上安装摄像头拍摄图像传到终端，人眼识别覆冰导线图像，经过除噪、滤波、边缘检测等图像预处理后，利用相机像素比例关系算出覆冰厚度。近年来，基于图像处理的线路覆冰厚度在线监测受到国内外很多学者的追捧，但这种方法让学者们把注意力过多地集中在图像处理上，而忽略了图像采集过程中的诸多问题，同时也缺乏系统的论证，得出的覆冰厚度值误差较大。

为解决上述问题，设计了一种基于图像技术、利用相机小孔成像原理的测量模型。为适应智能手机相机拍照特点，通常采用改进的张正友相机标定法[10]，得出相机的内外参数，但相机标定的主要任务是得到相机内部参数，利用图像物理尺寸与像素点数的比例关系求出每一英寸的像素点数αx、αy，与焦距f的比值便是fx、fy，通过图像缩放光轴中心不变的定理求出u0，v0。利用小孔成像、几何相似原理设计线路覆冰厚度测量模型，利用智能手机拍照试验，拍摄多组试验数据来验证模型的正确性及精确度，最后进行误差分析。

1 适应智能手机的相机标定法

摄像机模型其实就是简化的光学成像模型，即常见的针孔成像模型。相机标定是通过数学变换和矩阵计算来求解相机内外部参数的过程，方法分为传统相机标定法和自标定法两大类，而传统相机标定法有两点法、共平面法、张正友相机标定法等。

1.1 坐标系转换

为了方便描述后面的小孔成像模型，将三维的世界坐标转化为二维的像素坐标，为后续的模型计算做准备，以下建立了几个坐标系：世界坐标系、像素坐标系、图像坐标系、相机坐标系。各坐标系统如图1所示。

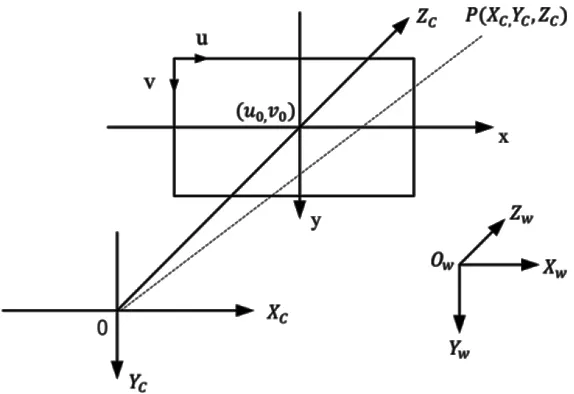
图1 各类坐标系

世界坐标系(Xw,Yw,Zw)是视觉系统坐标系，P是世界坐标系上任意一点，像素坐标系与相机坐标系均以世界坐标系为参考标准。相机坐标系由XC轴、YC轴、ZC轴组成，像素坐标系（u,v）是相机成像面上的二维坐标系，以pixel为单位，表示图像行与列方向的像素点数。图像坐标系（x,y）的原点交像素坐标系于(u0,v0)，相机坐标系的ZC轴经过像素坐标系交于点(u0,v0)，这里ZC轴指光轴，与像平面u，v垂直，同时，相机坐标系的XC轴、YC轴分别与像素坐标系的u轴、v轴平行。已知相机镜头中心到成像面的距离为焦距f，图像坐标系z轴与摄像机坐标系ZC重合，则相机中任意一点P（XC，YC，ZC）投影到图像坐标系上为点（x,y,f）。

1.2 标定过程

为适应本研究的需要，首先标定相机内部参数，即先确定fx、fy与主点（u0，v0），再利用上述张正友相机标定方法得出相机外部参数，由于本课题下述的模型计算主要利用相机的内部参数，下面将详细叙述相机内部参数的标定过程。

采用智能手机全屏拍照模式，图像分辨率为1 968×4 144，手机显示屏的物理尺寸为横向6.8 cm，纵向14.3 cm，故dx=0.034 6，dy=0.034 5，手机相机焦距f=4.52 mm，故fx=130.635 8，fy=131.014 5。

当相机拍摄的焦距发生变化时，图像上物体会产生缩放变化，但光轴不变，光轴与像平面的交点（u0，v0）不变，所以，利用相机的不同焦距拍摄同一物体，假设相机从f1变为f2，则：

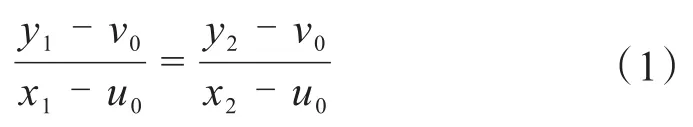
式中，(x1,y1)是相机焦距为f1时物体上的特征点图像坐标，(x2,y2)是相机焦距为f2时物体上的特征点坐标。在拍摄目标物体时多取几组这样的特征点坐标代入式（1）中，便可计算出u0，v0。本试验所用相机u0=1 090.685 1，v0=2 086.842 0。

2 输电线路覆冰厚度测量模型

2.1 测量模型的建立

在测算导线覆冰厚度模型中，通过摄像机标定，得到相机内部参数fx,fy,u0,v0，与此同时，尽量做到像平面与待测覆冰导线平行，根据相机小孔成像原理及图像与实际待测目标的空间几何关系得到待测覆冰导线厚度的实际值。又依据相机与地平面的关系建立了图像像素坐标系与世界坐标系距离的几何模型，如图2所示。

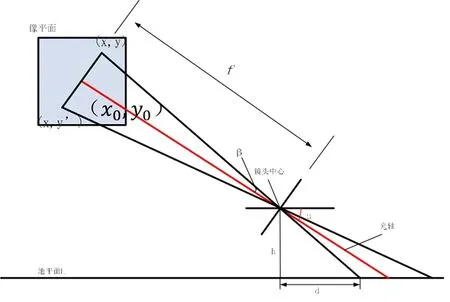
图2 测量深度值的几何模型

图2中，L代表地平面，h为镜头中心到地平面的垂直高度，d为像素坐标系与世界坐标系的水平距离（深度值），光轴与像平面垂直交于(x0,y0),即像素坐标为（u0,v0），像素坐标（x,y）表示覆冰线路上冰面最高点。α为相机俯视角，β为光轴与上边缘光线的夹角，f为相机设定的焦距，在以下的模型计算中，已标定的相机内部参数及焦距保持不变。

则：

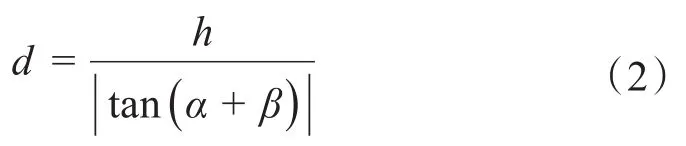
智能手机拍照过程中，覆冰图像会按一定比例系数放大，α+β很有可能会大于90°，故加上绝对值，其中，

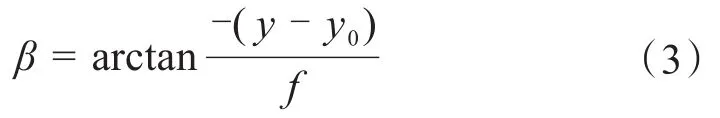
结合（2）（3）式可得：

根据图3所示图像坐标与像素坐标几何关系可知：

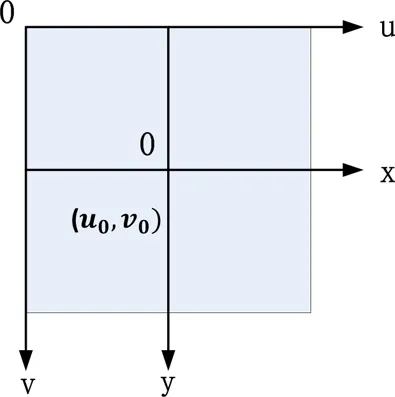
图3 图像坐标与像素坐标转换模型

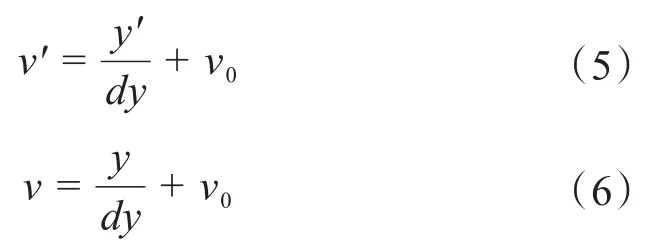
即可得y=(v-v0)dy,则yy′表示图像中覆冰导线垂直方向像素差值，dy表示每个像素点的平面距离。

根据相机小孔成像原理，建立如图4所示覆冰导线像素映射模型。

在如图4所示模型分析中，将覆冰后的导线看作理想规则的圆柱形，垂直截面是规则圆形，在实际测量中，摄像机架设高度h和相机仰视角α会随着测量的需求发生变化，但各成像面之间的相对夹角不变，∠PMH=∠PNH=∠MNB=90°，PO⊥yy′，MN⊥PH交于点B，∠HMB=∠HNB=β。H表示圆心，HM、HN表示圆H的半径，PM、PN为切线。根据几何相似原理可得：

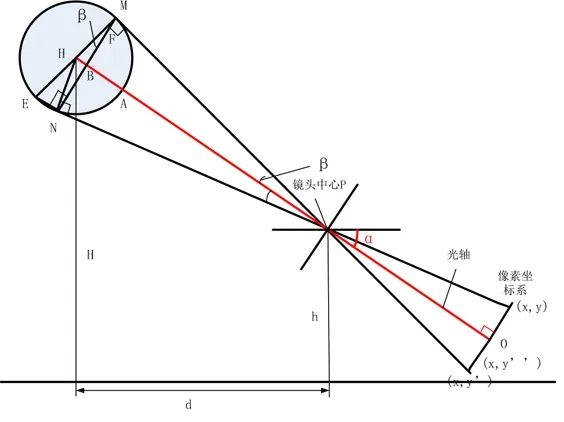
图4 覆冰导线像素映像模型

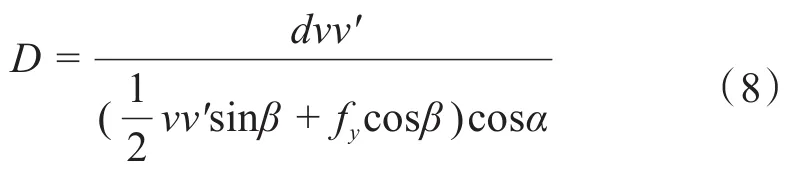
h是相机架设的高度，α是相机俯视角，这些可通过测量直接得出。D表示覆冰导线直径，vv′表示图像中覆冰导线垂直方向上像素值差值，fy为相机内部参数。

已知未覆冰输电线路直径D′，考虑到智能手机拍摄过程中，目标覆冰图像会存在放大比例系数k，则覆冰厚度d′计算公式如下：

2.2 结果与分析

本研究使用智能手机拍摄目标图像，经过相机标定后，相机内部参数为：fx=130.635 8，fy=131.014 5，u0=1 090.685 1，v0=2 086.842 0。模拟输电线路覆冰后，阈值为150的边缘分割图像如图5。

图5 阈值150的边缘分割图像

图像尺寸为1 968×4 144，焦距f=4.52 mm，相机采用全屏拍摄模式，手机屏幕斜对角长15.4 cm，则图像分辨率=756.736 8(pixel)，相机镜头中心到地平面的垂直高度h=56.838 1 cm，俯视角α=14.5°。通过测量实际覆冰厚度作为参考值，实际覆冰导线覆冰厚度为2.6 cm（本试验测量的是冰柱凸起部分最大覆冰厚度，凸起冰柱右半段按均匀覆冰近似处理，以测量上冰面覆冰厚度值为准），通过阈值分割处理图像后，沿冰柱直径方向选取像素坐标Smax（714，1523），Smin（903，2028），则直径方向像素坐标差值 vv′=539.21，-(y-y0)=269.605，图片放大比例系数k=4,未覆冰导线直径D′=1.94 cm，将以上数据代入公式（8），（9）可以测算出覆冰线路总直径D=7.012 6 cm，覆冰厚度d′=2.566 3 cm，相对误差约为-2.45%，可见模型测量误差较小。

为验证不同覆冰厚度测量模型的精度，本研究从不同拍摄高度、不同角度、不同距离拍摄来测量直径不同的规则圆柱直径，结果如表1所示。

2.3 误差分析

表1数据表明不同环境下测量的覆冰线路总直径会存在不同的相对误差，经试验研究分析，误差主要来源于相机拍摄高度h与俯视角α的测量误差，以及像素坐标选取带来的误差，而像素坐标差值vv′改变±5%都会给最后的测量结果带来非常大的变化，远远超出本文的误差范围，故表中vv′应保证绝对的准确性。在一定范围内分别改变h、α的值对最后的测量结果误差进行分析，表2为α不变、h变化10%的分析结果，表3为α变化10%、h不变的分析结果。

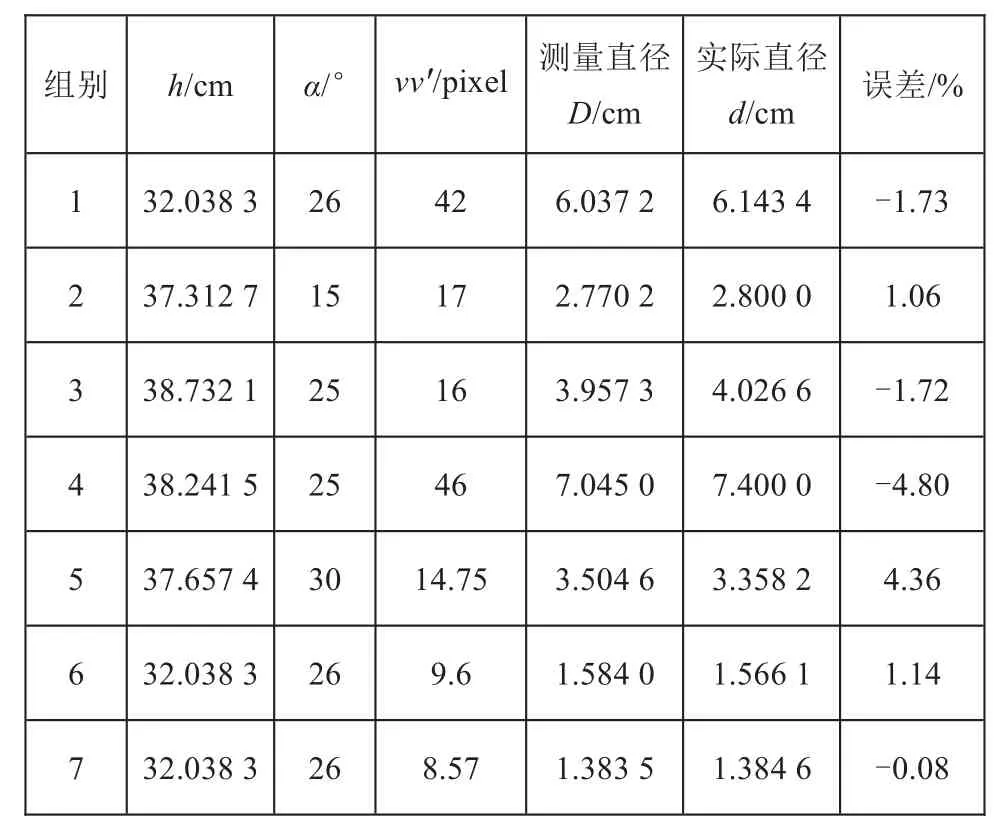
表1 不同直径圆柱测量数据

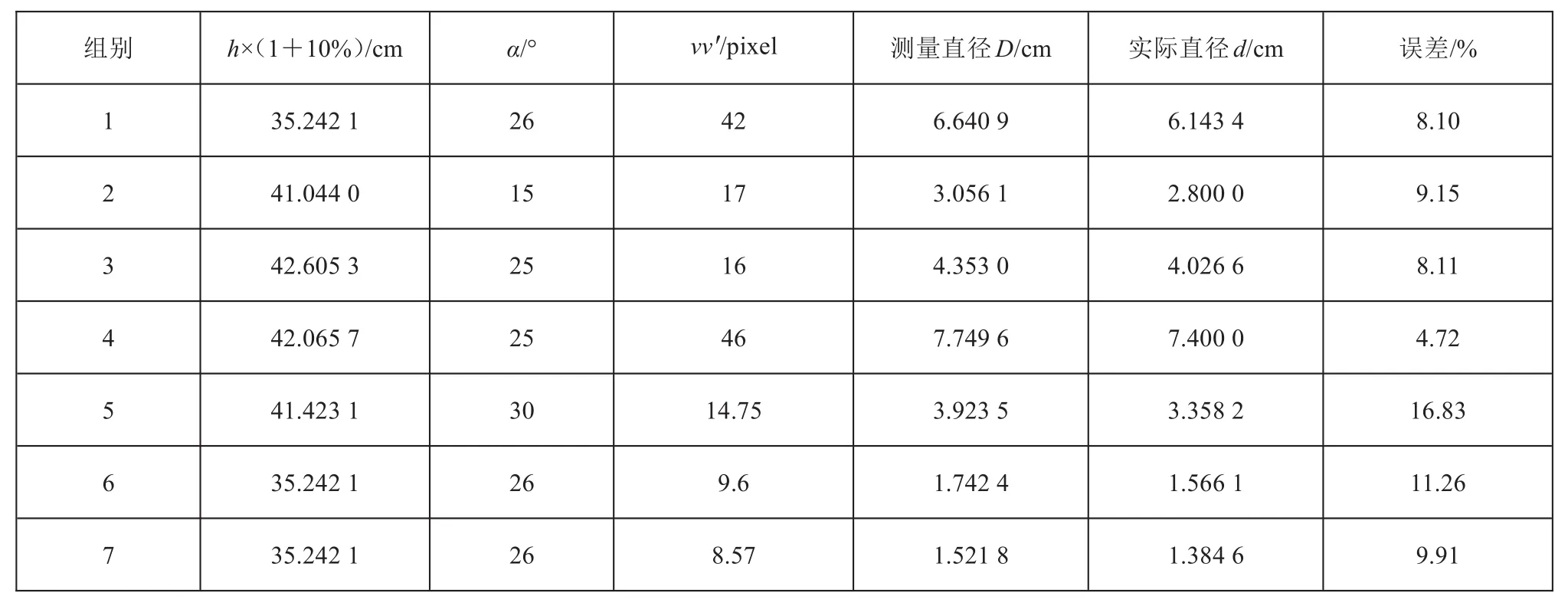
表2 α不变、h变化10%的误差分析

通过表2～3数据可知，h不变、α变化10%相对误差变化幅度明显大于α不变、h变化10%相对误差变化幅度，这说明α测量误差对测量模型得出覆冰厚度误差影响较大。由上文可知，考虑到镜头的切向畸变，目标覆冰线路应尽量处于图像中间位置，在采集图像时，主要通过调整相机拍摄角度达到这一目的，这可解释α测量误差较h而言对最后的测量结果影响较大。

3 结论

基于图像技术，利用相机小孔成像原理设计了覆冰导线厚度测量模型，结合三角形几何相似定律，推出导线覆冰厚度计算公式，在采集图像的过程中记录下相机拍摄高度h、相机俯视角度α以及未覆冰导线直径D′，利用相机标定求出相机内部参数，将以上数据代入公式得出模型测量值。为验证模型的准确性，收集整理了不同环境下，不同覆冰线路模型测算结果，并对其进行误差分析，发现模型测算覆冰厚度的相对误差主要来源于h、α的测量误差，而α的偏差对最后测算结果影响更大。

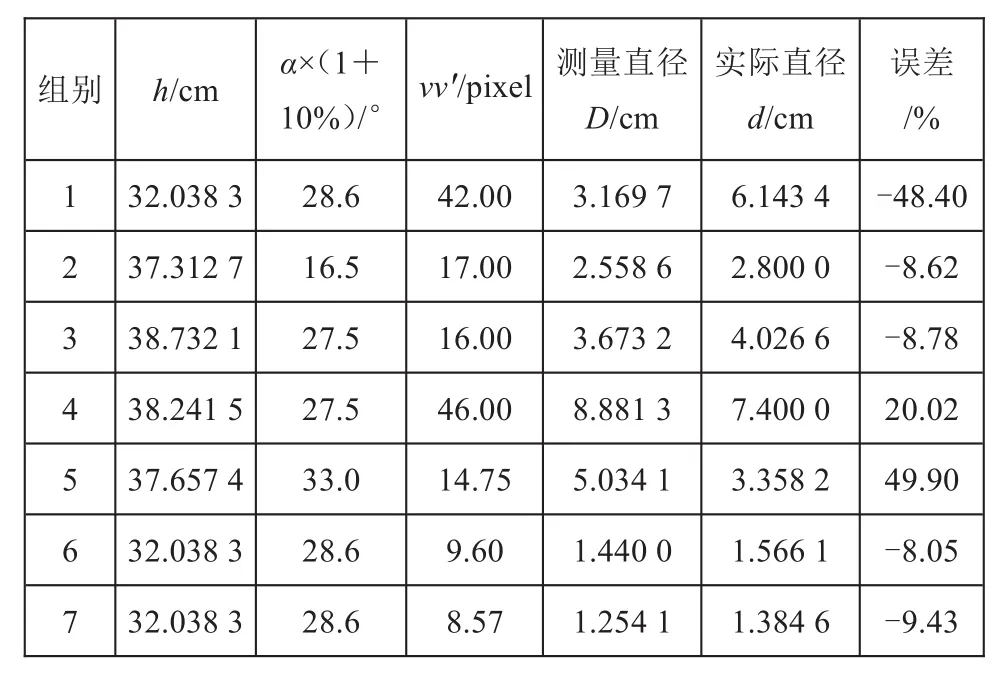
表3 α变化10%、h不变的误差分析