基于粗糙集理论的天然气处理厂综合能效评价研究

袁志华 朱祯 陈瑞熙

（1.西南油气田分公司川东北气矿；2.西南油气田公司川中北部采气管理处；3.西南石油大学石油与天然气工程学院）

某天然气处理厂是其气田企业地面工程的核心，是由装置、设备、管网等组成的工艺网络。其任务是从井口收集采出液（气、水），输送至计量站、转运站、集中处理站进行计量、分离、净化等，最后出口。该天然气处理厂的生产过程是一个相互作用、相互制约、相互关联的复杂生产过程。由于其系统庞大，系统分散，热损失大，管理难度大，从而制约了该天然气处理厂效率的提高。为达到节能减排、提质增效的目的，必须形成一套针对处理厂综合能效评价体系，找出能源利用中的薄弱环节，帮助气田企业降低生产成本，优化企业成本结构。

1 基于粗糙集理论的能效评价方法

粗糙集理论是一种数学工具，可以用来分析、推理和挖掘数据之间的关系，发现隐藏的知识，探索数据之间潜在的规律[1]。由于粗糙集自身的特点，它广泛应用于综合评价中[2-5]。

1.1 评价体系指标确定及范围选取

基于天然气处理厂能效评价指标体系的层次性和可操作性原则，并根据其自身的结构特点，将该评价体系划分为以下三个层次：一级指标：即天然气处理厂；二级指标：天然气处理厂能效评价体系的二级指标，即系统的各能效指标，包括新鲜水能效指标、电能能效指标、自用气能效指标和甲醇能效指标，这些能效指标构成评价指标体系的二级指标；三级指标：即新鲜水能效指标、电能能效指标、自用气能效指标和甲醇能效指标所对应评价体系的基本元素。

对于三级指标而言，每个指标最优参数范围。通过HYSYS软件对天然气处理厂进行模拟，结合参考设备的铭牌参数和调研相关文献、标准，可以确定各个指标的参数范围[6]。其中三级指标的指标类型有正向与逆向两种，正向表示增加了装置或整个系统的能效；逆向则相反。

1.2 评价体系的指标权重计算

设S=(U，A，V，f)是一个基于粗糙集理论的知识表达系统，C是条件属性，D是决策属性，且C⋃U=A,C⋂D=∅，D对C的依赖度τ可定义为

式中：Card为集合中元素的个数，即集合基数；POSCD为集合D关于C的正区域。

式（1）称作集合D在τ程度上依赖于集合C，记作C⇒τD。显然τ∈[0，1]，若τ=0，表示D中属性完全独立于C中所有属性；若τ∈(0，1)，表示D中属性部分依赖于C中属性；若τ=1，表示D中属性完全依赖于C中属性。

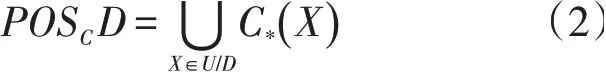
式中：U/D表示依据决策属性D对论域U进行的划分。

对于决策表来说，粗糙集理论中用粗糙度的概念表述条件属性对于决策属性分类的近似程度。粗糙度的公式为

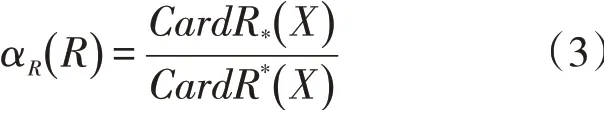
在粗糙集理论中，引入了相对重要度这一概念以表征Ci对于D的重要程度，即从集合C中去掉某一属性Ci时，决策属性集合D关于C的正区域将受到的影响，计算方法如下：

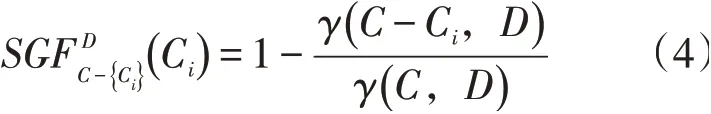
基于粗糙集理论的条件属性的权重就是该条件属性相对重要度与所有条件属性相对重要度和之比，即：

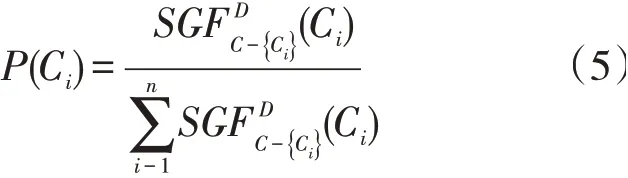
1.3 评价体系最终评价分数结果

通常难以用一个明确的值来对客观事物或者现象进行描述和度量，而模糊隶属函数，就是在该过程中，表示该事物或者现象模糊程度的函数。模糊隶属函数法就是利用隶属度函数进行模糊综合评价。通过指标无量纲化处理使其具有可比性，才能进行综合评价。在模糊数学中，常用[0，1]区间的一个实数来表示事物隶属于某一标准的程度。该函数就是描述事物或者现象的属性从属于某一标准到不属于某一标准的这个渐变过程的。

利用模糊隶属函数法对指标数据进行无量纲化处理后，根据所计算得到的各个指标权重，进行线性加权计算，从而得到最终评价结果。具体算法如下：

1）确定各个能效评价指标的上下限。

2）确定各个能效指标的模糊隶属度函数类型。

对于正向指标，采用升岭形分布模糊隶属度函数模型，即：

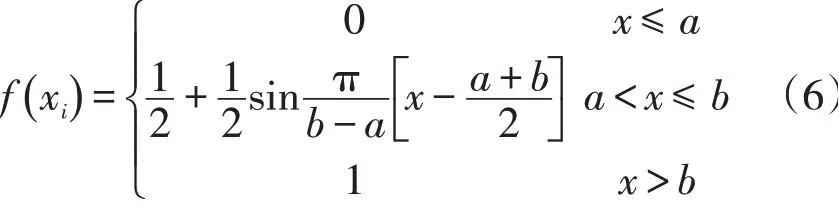
对于逆向指标，采用降岭形分布模糊隶属度函数模型，即：

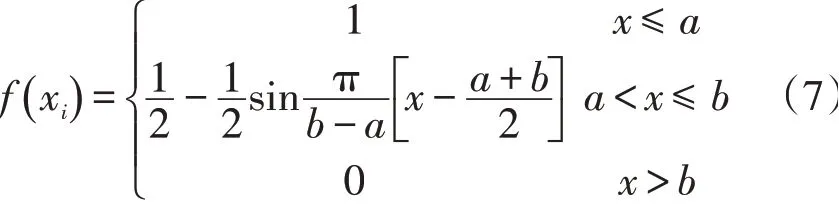
3）进行模糊变换及标准量化。利用模糊隶属度函数求得的指标模糊隶属度值f(xi)是在0～1的实数，消除了指标量纲的影响。习惯上将指标模糊隶属度值乘以100，作为指标的评价标准值，即：

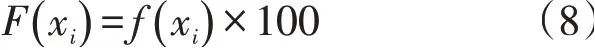
4）准则层各指标的最终得分：

式中：Fi为第i个准则层指标的评价值；Fij为第i个准则层指标的第j个指标层指标的标准量化值；wij为第i个准则层指标的第j个指标层指标相对准则层的权重；i为要评价的准则层指标的序号；j为要评价的准则层指标下的指标层指标的序号；n为要评价的准则层指标的指标层指标的数目。

5）被评价目标的综合评价得分：

式中：F为被评价指标体系的综合得分值；Fi为被评价指标体系中第i个准则层指标的得分值；wi为被评价指标体系中第i个准则层能效指标相对目标层的权重；i为被评价指标体系中准则层指标的序号；m为被评价指标体系中准则层指标的数目。

2 某天然气处理厂能效评价体系建立

1）确立各级指标。结合该天然气处理厂的工艺流程与实际情况，结合相关标准文献处理厂综合评价指标[7-10]见表1。

表1 处理厂综合评价指标

2）指标范围确定。工艺流程HYSYS模型见图1。将HYSYS模型的各个节点参数与实际调研所得数据对比，HYSYS模型准确性认证见表2。

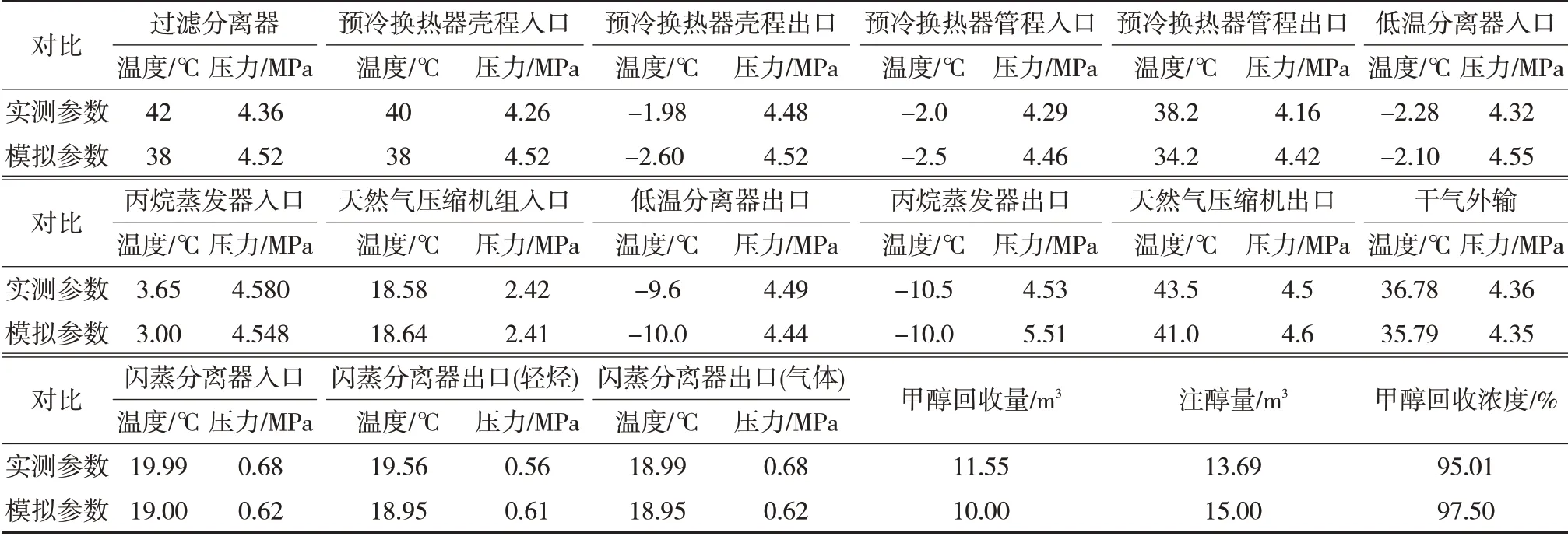
表2 HYSYS模型准确性验证

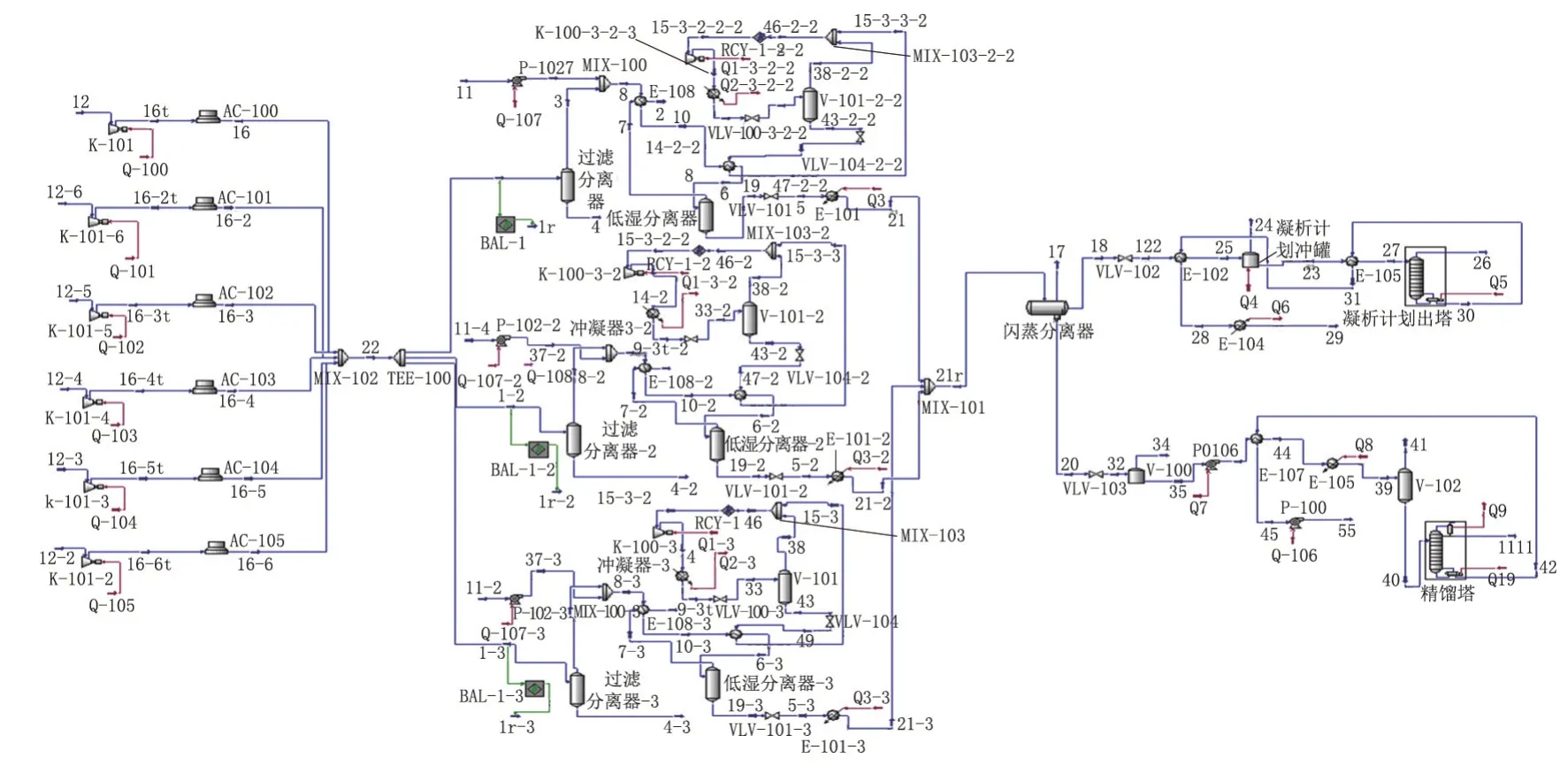
图1 工艺流程HYSYS模型

通过对比HYSYS模型与实际生产报表中关键设备数据与模拟工况中关键节点的数据，发现模拟的结果数据与实际生产报表数据基本一：（有些误差在工程中可以忽略不计），验证了HYSYS模型的准确性。

以C11为例，展示参数范围取值过程。在模拟计算过程中，控制环境温度为25℃，大气压力为一个标准大气压，压缩机其它参数保持默认设置。分别选取进口压力为1.90、1.95、2.00、2.10、2.15、2.20 MPa，压缩机压缩机进口压力变工况运行参数模拟结果见表3。

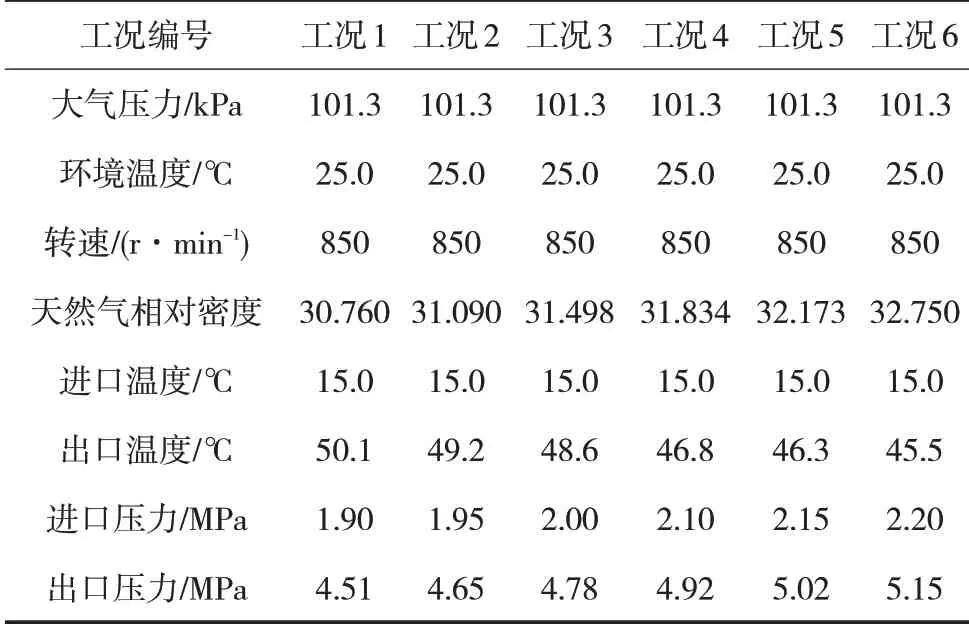
表3 压缩机进口压力变工况运行参数模拟结果

压缩机进口压力与压缩机效率的关系见图2，当压缩机各级进口温度、出口压力及压缩机转速不变时，随着进口压力的提高，压缩机的效率随着进口压力的升高而迅速下降，能效降低。综上，最终将进口压力范围为1.96～2.21 MPa。得到的天然气处理厂三级指标参数见表4所示。

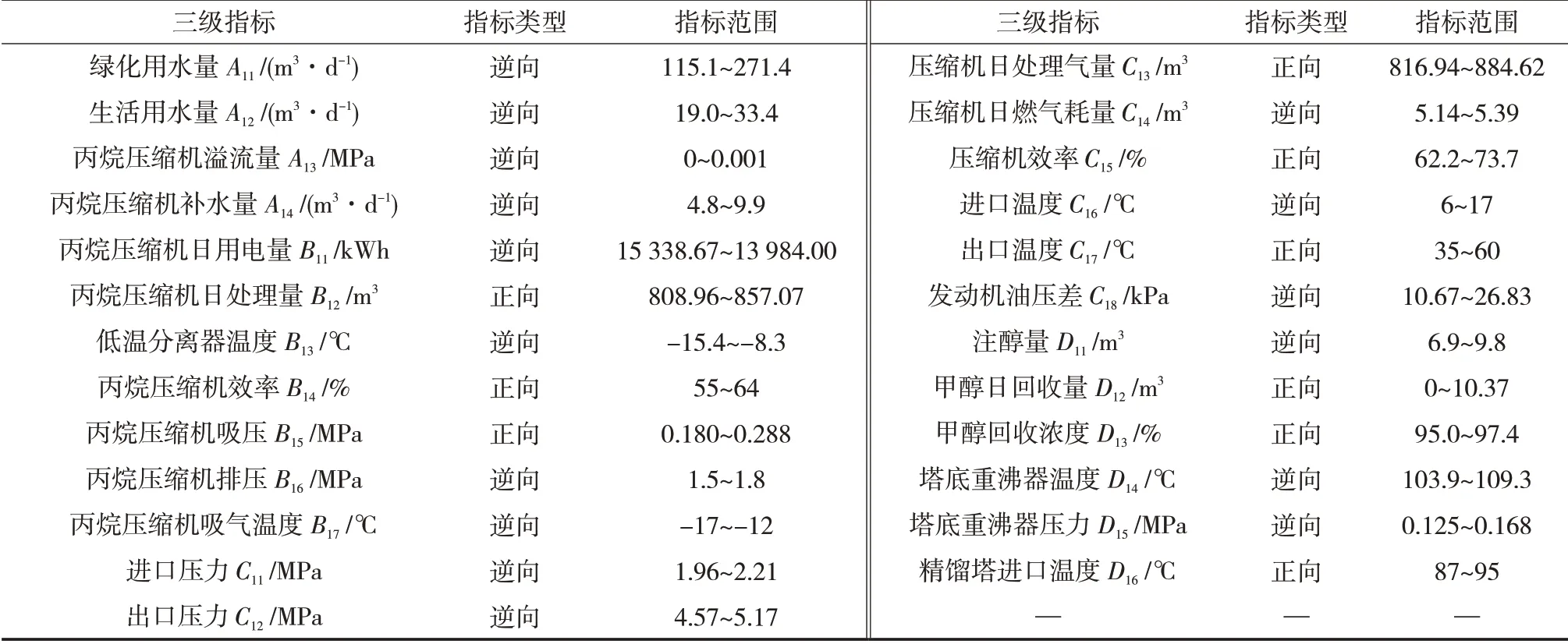
表4 三级指标参数

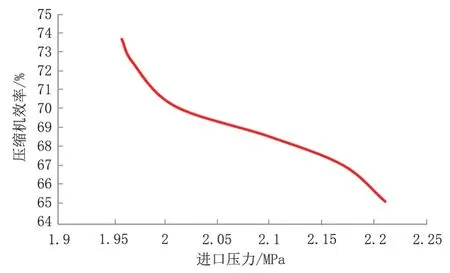
图2 压缩机进口压力与压缩机效率关系

3 某天然气处理厂能效评价体系评价结果

基于粗糙集理论，利用Python语言辅助处理数据，三级指标属性重要度与权重计算结果见表5。

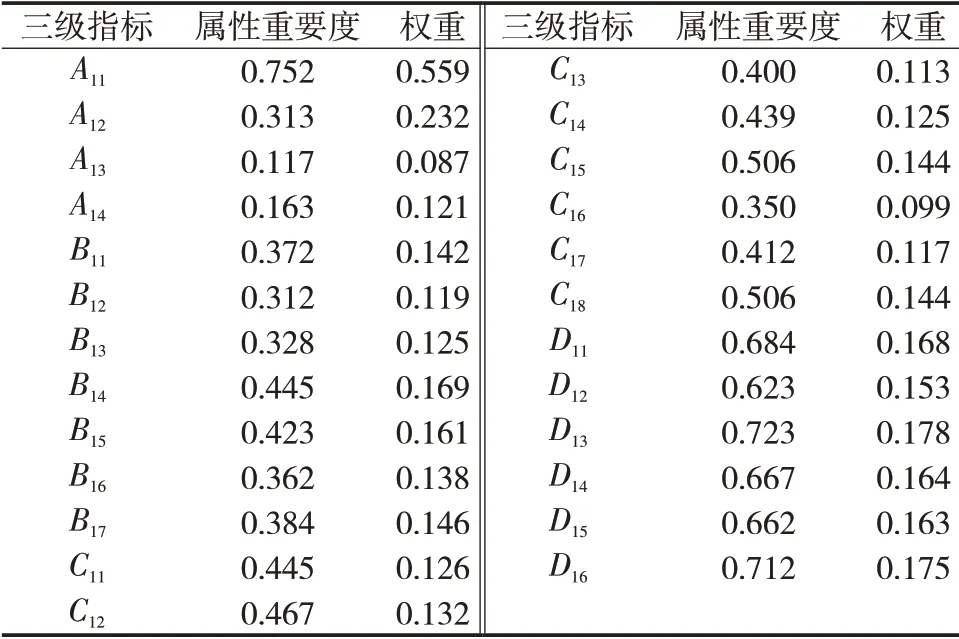
表5 三级指标属性重要度与权重计算结果

根据上述三级指标的40个样本数据，将对应单元的各项指标的单位样本数据进行相加，结合等距离离散的原则，首先建立二级指标决策表，参考三级指标计算步骤，可以得出二级指标属性重要度和权重得分结果见表6。

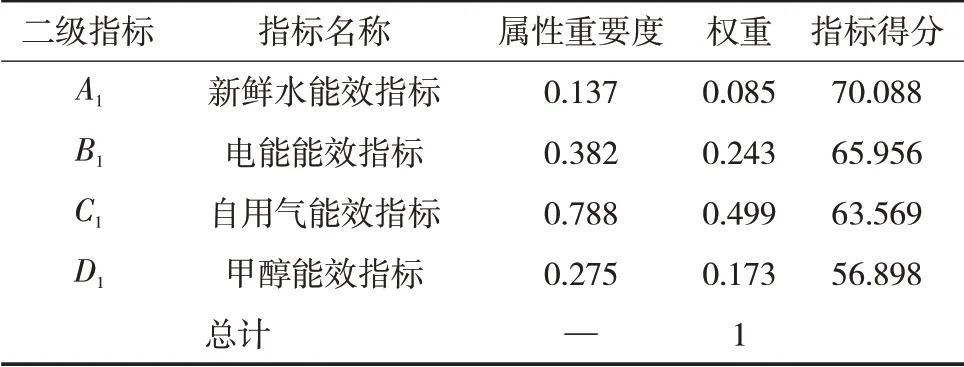
表6 二级指标属性重要度与权重得分结果

4 结论与建议

本文基于粗糙集理论建立了某天然气处理厂的综合能效评价体系，并对某天然气处理厂进行了评价，可以得出如下结论：

1）HYSYS模型用于模拟天然气处理厂的各项工艺参数的结果较为准确，能够模拟实际工况下的工艺参数，从而可以得到评价体系各三级指标的指标范围。

2）天然气处理厂综合能效评价体系中各二级指标的权重重要度顺序为自用气能效指标、电能指标、甲醇回收指标、新鲜水指标，可见对于该天然气处理厂，自用气部分是能效评价中最为重要的一部分。

3）对该天然气处理厂进行评价得分可以看到，新鲜水能效指标、电能能效指标以及自用气能效指标的得分相对较高，相比之下，甲醇能效指标的得分较低，因此在提质增效方面要重点从甲醇能效指标入手，比如进行甲醇回收-注入循环等措施。