适应于极区的惯导系统传递对准技术研究*

高贤志，原 润，蔡善军，郭瑞杰，马小艳

(1.海军装备部驻北京地区第三军事代表室·北京·100074；2.北京自动化控制设备研究所·北京·100074)

0 引 言

随着军事科学技术的发展及国际政治、经济、军事形势的多变性，各军事强国对武器系统的快速反应能力和全球作战能力均提出了更高的要求，要求武器系统在必要时可以穿越极区，而极区飞行可以实现直线飞行、缩短航程、增加有效作战载荷量、节省燃油、降低成本。另外，随着全球气温不断变暖，极区的经济价值及军事地位获得了逐步提升，世界各个经济政治强国都在不断地加强各自在极区的军事存在，以实现自身的经济利益。为保护我国在极区活动中的合法经济利益，提升我国在极区事务中的话语权，有必要针对极区的典型环境，开展相关技术研究，增强我军在极区执行护航、保护经济利益的能力，以及舰艇、飞机和武器装备在极区的作战能力。

惯性导航系统由于能够提供载体连续、自主、隐蔽的速度、位置、姿态等信息，在航空、航天、航海等军事领域以及许多民用领域中都得到了广泛应用。指北方位的惯导力学编排由于具备物理意义明确的优点而得到了广泛的应用，但其位置更新、特别是经度更新需要使用纬度的正切项。正切项在高纬度地区会变得很大，在极点会变为无穷大，使得导航计算出现溢出现象。针对这一问题，国内外学者均进行了研究，现有的解决方法主要有极圈导航(也称平面导航)、横向导航、虚拟圆球的极区导航算法，基于凝固地理系和格网导航。极圈导航是指在进入极圈之前，导航坐标系采用地理坐标系，在进入极圈之后，导航坐标系固定为进入极圈点时的地理坐标系，但该坐标系适用范围小，存在原理性误差。横向导航重新定义了地球固连直角坐标系，将赤道上的两点作为南北极点，在极区可以进行正常解算，输出横向经纬度。但是，当载体运动到横向坐标系的高纬度地区时，又需切换至常用的地球固连直角坐标系。为了适应全球导航，需要在两种坐标系之间进行切换，且横向经纬度的输出与常用的地图数据并不兼容，不方便使用。凝固地理系将原点从地心挪到了椭球面，其力学编排适合全球导航，但过长距离的导航使得凝固地理系下的导航参数失去了直观的物理意义，最终需将参数转换到地理系下才能表征载体的运动状态。基于虚拟圆球法向量的极区惯性导航算法用四维向量替代了常规的三维向量的位置表示方式，将四维向量进行转换，可以得到常规意义上的三维位置信息，避免了出入极区的切换，具有全球适应性。格网导航以格林威治子午线作为飞机航向参考，可避免由纬度升高、经线收敛而造成的定向参考难题，其输出的地心固连直角坐标下的位置信息，可方便同极区航图使用。因此，格林威治格网导航编排是目前较为适宜的极区惯性导航编排方案。为了适应全球航行，若采用了格网导航，飞机、舰船等平台所用的惯导系统输出的导航参数中的姿态和速度信息均是在格网坐标系下表示的，位置信息是由地心固连直角坐标系给出的，而关于子惯导如何基于格网导航信息进行对准，则需要进一步展开研究。

1 极区传递对准方案

传递对准是动基座对准的一种方法，是指载体航行时，载体上需要对准的子惯导利用已对准好的主惯导的信息来进行对准的一种方法。动基座传递对准在国外得到了广泛的应用，如美国“捕鲸叉”(AGM/RGM/UGM-84 Harpoon)舰载导弹、法国和意大利“紫苑”(Aster)舰载导弹、瑞典“RBS-15”舰载导弹、俄罗斯“KH-35 Uran/Bal”舰载导弹的对准，都应用了传递对准技术。几十年来，国外众多研究者致力于对传递对准模型、传递对准误差的补偿、滤波算法以及仿真验证等方面的研究，以提高传递对准的精度、速度和鲁棒性。

根据不同参数的差值，可以将传递对准分为两大类：计算参数匹配和测量参数匹配。计算参数匹配包括速度匹配和位置匹配，测量参数匹配包括角速率匹配、姿态匹配和加速度匹配。一般而言，计算参数匹配法的对准精度较高，但对准时间较长；测量参数匹配法的对准速度较快，但精度易受噪声和载体挠性变形的影响。针对现代战争对武器系统快速反应的需求，1989年，美国学者首次提出了姿态角匹配概念，以及“速度+姿态”匹配快速对准方法，将动基座传递对准带到了一个全新的发展阶段。“速度加姿态”匹配对准算法的一个显著特点是提高了对准的快速性，在估计方位失准角时无需进行时间较长的S形机动，只需做一个简单的摇摆机动，便能在极短的时间内对子惯导的三个失准角做出精确的估计。“速度加姿态”匹配对准算法不仅适用于机动能力较强的机载武器传递对准，对于舰载平台武器系统的传递对准，通过海浪的自然摇摆，也能在短时间内对航向失准角和水平失准角进行估计。

为了实现极区的动基座传递对准，文献[11]设计了格网坐标系的“速度+姿态角速率”匹配，实现了极区的传递对准，但该方法对采用了旋转调制技术的主惯导适应性较差。旋转调制是当前各国为了实现长航时高精度惯性导航而广泛采用的经济可行的方案，它在捷联惯导系统的基础上引入了转动机构，通过旋转机构带动惯性测量单元转动，以调制惯性器件的误差，在飞机、舰船等领域中也得到了越来越广泛的应用。但是，转位机构在提高了惯导精度的同时，也使得主惯导系统的导航信息品质发生了变化，其误差中不仅存在惯导系统特有的舒拉振荡以及地球振荡，还存在由转位机构引入的转动频率。子惯导一般采用捷联模式，两者的角速率受旋转机构的影响而不一致，进而影响了子惯导对准的精度。考虑到姿态角是姿态角速率的积分，积分环节的引入使得主子惯导的姿态匹配受旋转调制的影响相对减弱，因此本文将采用格网坐标系的“速度+姿态角”匹配传递对准方案。

1.1 格网导航算法编排

格网导航算法通过引入虚拟航向来解决航向输出的问题，格网导航坐标系(如图1中的

e

G

e

G

e

G)以所在地

P

点处平行于格林威治子午面的平面作为格网平面，以所在地的水平面作为切平面，将格网平面与切平面的交线定义为格网北向。格网北向与地理坐标系

e

e

e

的天向轴重合，与地理系真北方向的夹角为

σ

；地球直角坐标系

x

y

z

、格网导航系

e

G

e

G

e

G、地理坐标系

e

e

e

之间的关系示意图如图1所示。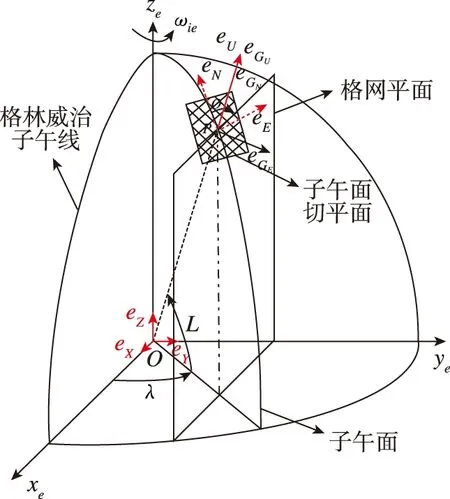

图1 格网坐标系定义示意图Fig.1 The schematic diagram of grid coordination

(1)

图1中，

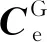
L

、

λ

分别为经纬度，

σ

为格网北向与真北向之间的偏差角,

ω

为地球自转角速度。

格网导航算法的姿态更新、速度更新以及位置更新方法与指北导航算法类似，即有

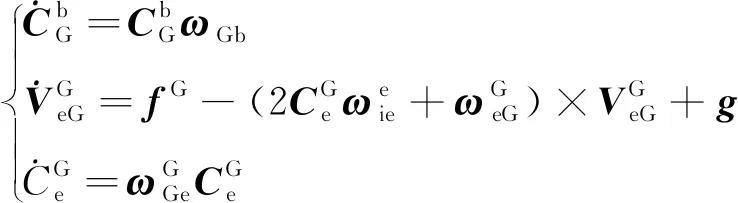
(2)

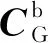
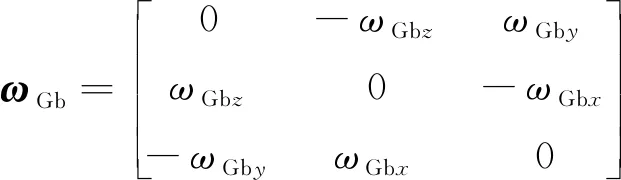
(3)

其中，

ω

Gb、

ω

Gb和

ω

Gb为载体相对格网导航系的角速率。

1.2 基于格网系的“速度+姿态”匹配对准算法

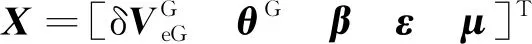
(4)

其中，速度误差方程为

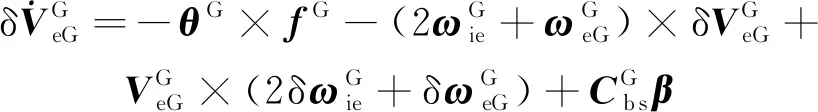
(5)

姿态误差方程为

(6)

加表零偏误差方程为

(7)

陀螺漂移误差方程为

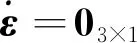
(8)

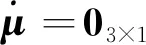
利用上述误差方程，可构建卡尔曼滤波系统状态方程为

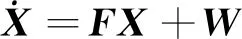
(9)

其中，为系统矩阵，非零元素可以从公式(5)、公式(6)得到，为系统噪声矩阵。

1.3 量测方程推导

将主子惯导的速度作差，即可得到速度的量测量，有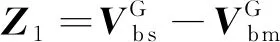

(10)

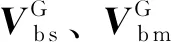
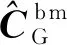
(11)

而当主子惯导之间的安装误差角为小角度时，可以表示为式(12)的形式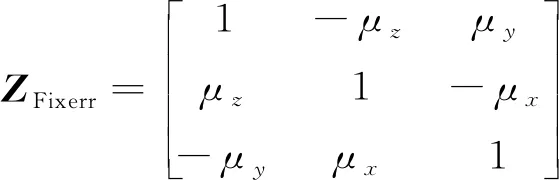

(12)

μ

、

μ

、

μ

为主子惯导间三个安装误差角的三个分量。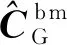

(13)

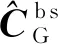
(14)

其中：为3×3的单位矩阵，(×)、(×)分别表示子惯导的三个安装误差角向量、子惯导安装误差角在子惯导坐标系下的投影的反对称矩阵。

同时，有

(15)

将式(9)、式(10)、式(11)代入式(7)，又可得

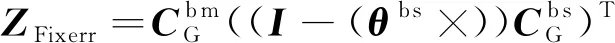
(16)

对照式(8)和式(12)，可得姿态匹配的量测方程

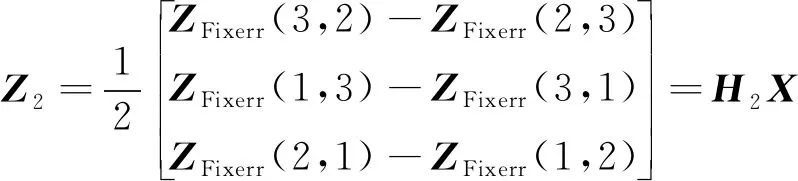
(17)

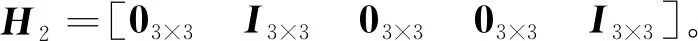
综上所述，“速度+姿态”匹配的量测方程为

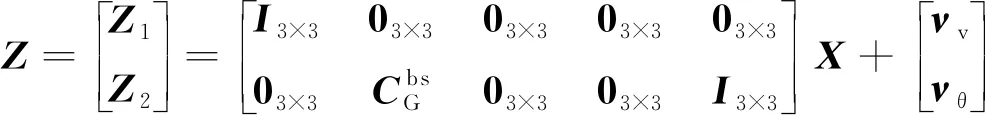
(18)

、分别表示主惯导速度，以及姿态测量误差。

2 理论仿真

为了验证本文提出的格网“速度+姿态”匹配传递对准方法，在高纬度条件下进行仿真，仿真条件为：

• 纬度：北纬45°和89.99°；

• 舰艇晃动角度：滚转、航向与俯仰角均为0.5sin(2πt/20)(°)；

• 子惯导安装误差角分别为：-0.2°、0.18°、-0.2°；

• 子惯导陀螺漂移为：0.5(°)/h；

• 子惯导加表零偏为：0.00001m/s；

• 仿真时间为260s。

采用格网“速度+姿态”匹配的安装误差角估计值分别如图2和3所示。其中，红色对应

Y

轴，蓝色对应

X

轴，黑色对应

Z

轴。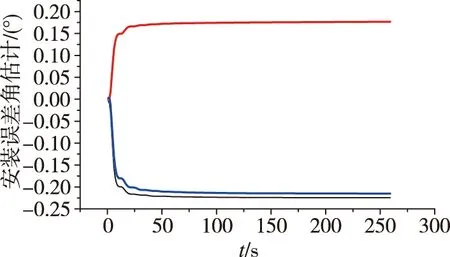

图2 北纬45°时的安装误差角估计值Fig.2 The estimate of installation error at 45°N

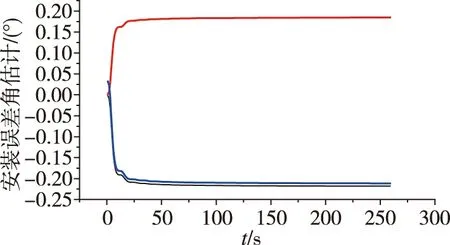
图3 北纬89.99°时的安装误差角估计值Fig.3 The estimate of installation error at 89.99°N

可见，无论是在中纬度还是高纬度地区，格网系的“速度+姿态”传递对准算法均可在30s内完成主子惯导间安装误差角的估计，三个安装角的估计误差均小于0.02°，满足舰载武器极区启动对子惯导系统提出的极区快速、高精度对准的需求。

3 试验验证

为了对算法进行验证，两型惯导系统在某试验船上开展了极区航行验证试验，其中一型为旋转调制型惯导系统(主惯导)，另一型为捷联惯导系统(子惯导)，子惯导在整个试验过程中自动重复进行对准及导航流程。

表1分别给出了北纬75°以上及75°以下的四条次30s传递对准时三个安装误差角的估计值，表2给出了对应8组对准完成、转导航后180s的纯惯性导航水平定位误差统计。

表1 不同纬度30s时的安装误差角估计结果Tab.1 The estimate of installation error in different latitude at 30s

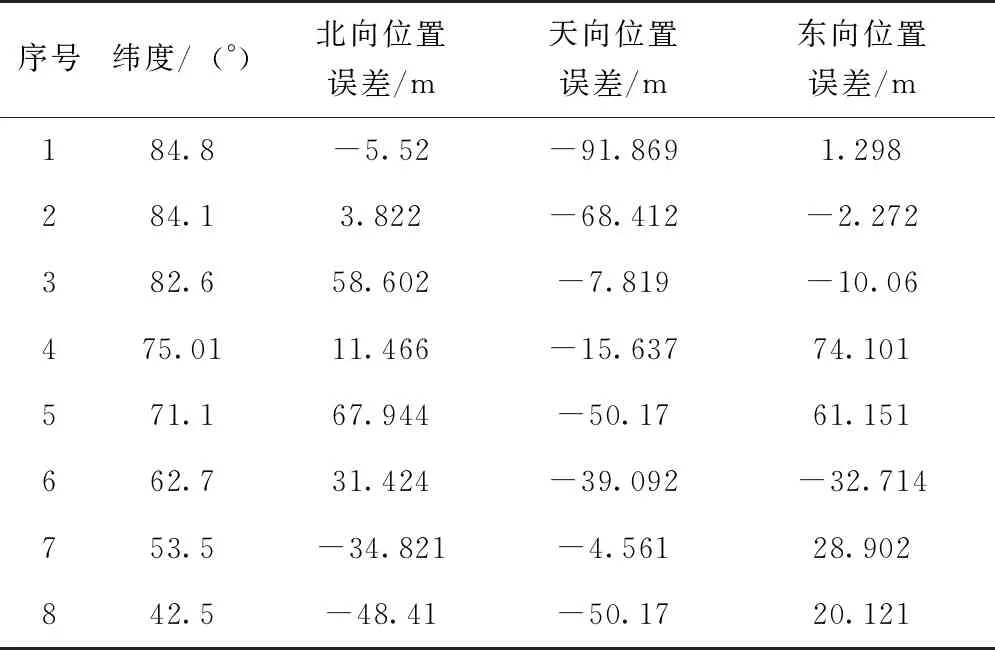
表2 30s传递对准后子惯导的180s纯惯性定位精度统计Tab.2 180’s position error of slave INS in different latitude at 30s

由以上可见，高纬度及中低纬度条件下的安装误差角估计误差基本一致，三个安装角的估计最大偏差小于0.1°，转导航后的纯惯性导航定位精度也间接验证了传递对准的精度，说明不同的纬度对传递对准几乎没有影响，进一步验证了不同纬度下传递对准算法的适用性。试验的精度与理论仿真的精度相比有所降低，这是由于在实际试验过程中受到了主子惯导之间的杆臂误差、时间延迟、挠曲变形等因素的影响。

4 结 论

本文给出的格网坐标系“速度+姿态”匹配的传递对准算法，可以满足全球导航的需求，并能适应于主惯导为旋转调制型惯导、子惯导为捷联惯导的新型传递对准的应用需求。理论仿真及海上实航试验结果均表明，采用格网导航系下的“速度+姿态”卡尔曼滤波算法，在舰船的典型摇摆运动及海上任意航行期间，在30s内均可实现子惯导极区的快速高精度传递对准。