在数学教学中，努力读懂学生

王筠妍

【摘要】《数学课程标准》指出：“义务教育阶段的数学课程，其基本出发点是促进学生全面、持续、和谐发展。它不仅要考虑数学自身的特点，更应遵循学生学习数学的心理规律。”强调任何的数学教学活动，都要从学生已有的生活经验出发，让学生亲身经历过程，进而使学生获得对数学的理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展。

【关键词】读懂;学生

当今课程改革的核心是关注每一位学生的发展。在数学课堂不应只是传授知识和技能，应该是师生互动、建构智慧生成的过程，这一切都必须要从读懂学生开始。要了解学生情感、知识、思维上的需求，在学生成长需要的基础上，精心预设教学。

一、为什么要读懂学生？

在教学中，老师们经常会有这样的困惑：

1.为什么总有学生提出一些我们没有预设到的奇怪问题？

2.为什么反复强调这个知识，学生还是错？

......

学生也存在困惑：

1.数学课上，老师都讲了半天了，我还是不明白。

2.今天老师老师让我们做了好多练习，重复的题都已经做了N次了。

......

出现困惑的原因是我们没有读懂学生。没有读懂学生已有学习经验和知识基础;没走进学生的世界，没读懂学生的心理。如果我们能了解学生的心理，读懂学生，以上的困惑就能够解决了。

《数学课程标准》特别提出：“要以学生的发展为本。”这也就是要求我们的教学是为学生的发展服务。所以我们在整个教学过程中都必须读懂我们的教学对象。

二、如何读懂学生？

1.努力读懂学生的学习起点。

学生跨进校门的时候，已经积累了许多生活经验。在不断的学习中，又积累了一定的知识，有自己的思维经验和方法。所有有效的数学教学活动都应该是建立在学生的认知水平和已有的知识经验基础之上的。既要关注学生“应有的学习起点”，也要重视学生“现实的学习起点”。我们发现学生“现实的学习起点”和“应有的学习起点”有很大的差距。因此，教学中如能读懂学生的学习起点，再进行教学，必将事半功倍。

（1）读懂学生的生活起点。

在数学教学中，我们要思考我们的学生在生活中已经积累了什么生活经验？如果能准确把握住这一起点，这样学生对新知识的理解就会变得更加容易，感悟就会更加深刻。

例如：在《年、月、日》一课学习之前，学生在生活中对“年、月、日”就有了自己的理解和感悟。这时我们不必一一概念式地填鸭介绍，可以请学生用自己的语言把生活中经历的一些事情，描述出一年、一月、一日大约有多长。

生1：今年春节到明年再过春节是一年。

生2：我的弟弟是今年11月18日出生的，明年的11月18日，我弟弟又长大了一岁，就是过了一年。

生3：老师从这个月领工资到下个月再领工资就是过了一个月。

生4：今天这时到明天这时就是一日。

......

学习“年、月、日”这样的内容不像学习时分秒，老师不可能让学生现场体验。课堂上，不妨放手让同学们七嘴八舌地说，回味已有生活经历。将学生记忆中的各种“年、月、日”的体验调入“前台”，轻松地把时间概念印在脑海里。如果我们可以读懂学生的生活起点，我们的数学课堂就会变得更“简单”。

（2）读懂学生的思维起点。

在教学中我们往往会发现，学生的思维方式和老师预设的有很大差别，我们应当尊重学生原有的思维起点。只有读懂属于学生自己的数学思维起点才能找到最适合学生的数学学习方法。

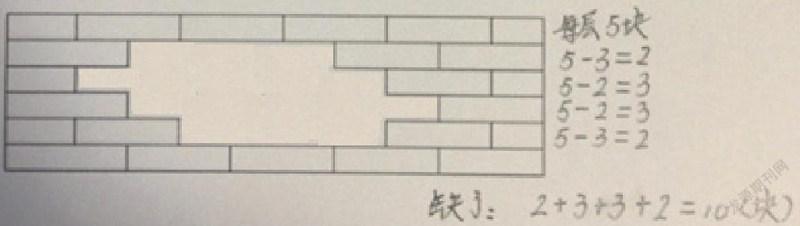
在一年级下学期，我们经常会遇见这样的题目，出现一面缺了砖的墙，问学生：缺了几块砖？

教学中很多老师会让孩子先画一画，再数一数。然而学生的画法并没有像我们老师所预设的，出现各种错误的画法，找不到正确的答案。老师们百思不得其解：为什么讲那么多次，学生还是不会？

这是因为我们没有找准学生的思维起点。一年级学生的空间思维弱，砖的排列规律对于他们来说也非常陌生，即使孩子画对了，因为一年级是使用铅笔的原因，画完以后数也是很容易出错。我们却要孩子画了再数，这样其实挺为难孩子。

有的孩子说这样更容易：

他是这样想的：“我发现每一层砖块的数量都是同样多的。数一数就知道完整的一层有5块砖（2个半块算一块）;然后一层层地看，数数每一层现在有几块砖，用每层一共的5块砖减去现在有的砖块数，就算出每一层还缺了几块砖;最后再把各层缺的砖加起来，就知道一共缺了几块砖。”

“水有源，故其流不穷;木有根，故其生不穷”，课堂上老师只有读懂学生的思维起点，从而说学生能理解的话，做学生能懂的事，学生才会说得好，做得棒。

2.努力读懂学生的学习过程。

学习过程是一个动态生成的过程，学生思维与新知识发生碰撞的一瞬间形成动态资源。读懂学生的学习过程，把握住课堂中意外生成的动态资源，因势利导加以利用，并及时调整教学方法，这样整个学习过程会更加灵动和谐。

（1）读懂学生的学习需求。

我认为，改善教学行为、进行课堂教学的重要出发点是：了解孩子的學习需求。

曾听过吴正宪老师上《角的度量》一课：学生认识了量角器后尝试测量角（30度的角）：

生1：这个角是30º。生2：不对，这个角是150 º。生3：这里看是30º，那里看是150º，到底是多少度呢？学生在议论，在争辩。

对于学生提出的疑问，吴老师并没有马上作出回答，她不慌不忙地拿出一个经过“加工”的量角器教具（这个量角器教具在中心点上系着两条红绳），一条红绳和圈里刻度线重合并固定不动，另一条红绳绕中心点不断旋转，30º，150º。老师接着不断地改变绳子的引出方向，学生在老师的操作下观察着、思考着、交流着。

课堂上学生出现疑问不解时，教师的采用的处理方法直接影响学生的学习进程和效果。课例中，由于吴老师读懂了学生，知道课堂上学生有什么学习需求，于是她针对教学难点，巧妙地创造学具，让学生在学具的幫助下阐述自己的观点，不断调整自己的认识，纠正认知偏差。

（2）读懂学生的学习障碍。

学生在学习过程中不可避免遇到“苦难”，遇到学习障碍。我们要读懂学生的学习障碍，并在这时候伸出援手，发挥教师的主导作用，在最恰当的时机以最恰当的方式帮助学生跨越障碍，学习的道路才会畅通无阻。

在教学《求一个小数的近似数》时，我遇到了这样的情况：

请写出下列各数的近似数：4.83（保留一位小数）（ ）

4.83（保留整数）（ ）

4.839（保留两位小数）（ ）

4.8396（保留三位小数）（ ）

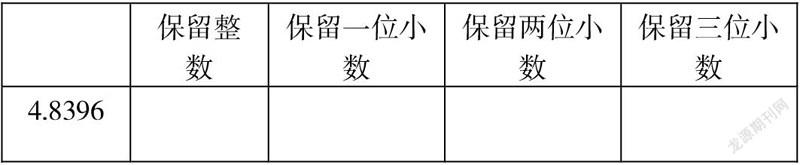
这样的题目学生基本都会做，但如果题目换成下面形式：

学生的错误率比前面的填空高很多。问题的实质都是一样的，为什么不同的形式，结果会出现这么大的差别呢？难道是学生没有掌握求近似数的方法？这和学生注意的广度有关！低年级学生，注意范围比较狭小，往往注意这个就忘掉那个，高年级学生注意范围则有显著发展。怎样让学生把注意力放到按要求保留的数位上，排除其他数位的干扰呢？我让学生把每一步要保留的部分用框标记，接着对它的下一位进行四舍五入。例如：4.8396（保留整数）、4.8296（保留一位小数）、4.8396（留两位小数）、4.8396（保留三位小数）。这样用方框把要保留的部分框下来，帮助学生记住他上一步的行为并把注意放在框起来的部分的下一位，消除其他无关数字的干扰，缩小到要注意的数字只有一个，学生只要会四舍五入，就能在任何形式下求近似数，准确率大大提高。

在学生学习过程中我们要读懂学生的学习障碍，想办法为孩子“架设桥梁”，让孩子“层层突破”，尝试到成功的甜。

（3）读懂学生的学习情绪。

我们常说，在课堂上要努力激发学生的学习兴趣。但只有读懂了学生的学习情绪，我们才能激起学生的学习兴趣，让学生爱上我们的数学课。

教育是一种洞悉，课堂上学生累了、不高兴了、需要鼓励了、需要启发了……这时需要我们老师有一双敏锐的眼睛，洞悉学生的学习情绪，从而选择有效教学方法和改变教学策略，让每个学生都带着好的学习情绪，愉快地进行学习。

3.努力读懂学生的学习收获。

努力读懂学生不但是只在课堂上，而是应该贯穿在整个学习阶段中。在课后老师要通过小测试、谈话、作业、日记等都多种形式了解学生的学习情况，读懂学生的学习收获。

（1）读懂学生的学习方法。

每个学生都是不同的个体，学习方法肯定各不相同。课后我们要根据学生不同的反馈，读懂学生的学习方法，进行适当的点播，才能使教学效果更佳。

在上完《经过时间的计算》一课后，我布置了这样的一道数学题：从12时50分到15时30分，经过了多少分？

学生有多种思考方法：

这次作业完成情况学生各有特色。针对这次作业，课后我根据学生的作业反馈，分析每一种方法，并进行优化，让孩子们牢固掌握知识。在教学中读懂学生的学习方法，读懂学生的精彩，能使学生的思维更充分地展示。

（2）读懂学生的学习错误。

学生在计算时经常会出现以下两种情况，很多时候我们老师以一句“粗心”来总结。

①号学生：85-15=100 ②号学生：49+27=66

①号学生对运算符号感知出现了偏差，本来是减法，计算时却按加法算，导致计算错误。这类学生初看觉得是粗心，实质是感知能力不完善。②号学生在计算过程中没有加进位，也没有标进位“1”的习惯。这类学生其实是概念不清、习惯不好、方法掌握不熟练。

我们在教学中只有读懂学生的学习错误，“对症下药”，才能“药到病除”。

山高水长，任重道远。希望我们都努力读懂学生，让学生享受学习的快乐。希望我们可以自信地对我们的学生说：“在学习这条路上，老师懂你。”

参考文献：

[1]董文华.让小学生恋上数学[M].北京：中国轻工业出版社，2013：70—72.

[2]吴正宪.给小学数学教师的建议[M].上海：华东师范大学出版社，2012：30—32、39—40.