基于MSPAC法的微动探测应用研究

金俊俊，索 朗，赵思为，张 硕

(中铁二院工程集团有限责任公司，四川 成都 610031)

1 引 言

环境噪声主要是由随机分布的不同类型的噪声源产生，包括体波、面波、散射波等共同组成的复杂波场，其中面波信号占据环境噪声中的大部分能量[1]。微动探测便是通过提取天然场源中的面波频散信息，研究地下地层速度结构。频散曲线提取是面波勘探的关键步骤，早期微动勘探面波频散曲线提取方法主要有FK法[2]、SPAC(Spatial Autocorrelation)法，由于SPAC法具有更好的稳定性，台站布置更为灵活，学者们对其法进行了深入的研究。Okada和Ling提出了ESPAC(Extended Spatial Autocorrelation)法，将SPAC法台站布设方式从传统的圆形扩展到嵌套三角形、直线形等更为灵活的排列方式，推动了微动技术在实际勘察领域的应用和发展。Ohori进一步对比了不同排列下ESPAC法和FK法应用效果，结果表明ESPAC法对不同类型排列方式均能够取得良好的效果，并且在低频段，比FK法具有更高的精度[3]。Asten等对比了嵌套三角形排列和圆形排列频散曲线提取效果，结果表明使用较少台站的嵌套三角形排列方式可以计算得到和圆形排列方式几乎一致的频散曲线，在成本方面具有较高的性价比[4]。Galiana等通过对ESPAC理论研究发现，仅利用两台台阵即可实现任意排列方式的数据采集，进一步提高了微动法野外条件的适应能力，降低了设备成本[5]。尽管线形排列方式野外布置简单，但不可避免会受到噪声源方位效应的影响， 为此，Cheng等提出了MAPS(Multichannel Analysis of Passive Surface Waves)方法[6]，通过地震干涉和MASW(Multichannel Analysis of Surface Waves)生成虚拟炮集，之后利用相移法计算频散曲线，解决了噪声源方位效应的问题。

在微动探测应用方面，刘杨等利用微动高分辨率频率—波数谱法进行地热资源探测[7]；徐佩芬等将微动技术应用于岩浆岩侵入、煤矿陷落柱、城市孤石、地层分层以及隐伏断层探测，取得了良好的效果[8-10]；黄光明等[11],李耐宾等[12]将微动技术应用于地下岩溶探测，徐兴倩等利用微动信号检测碎石土滑坡滑动面[13]；林朝旭利用微动技术探测城市地铁盾构区间孤石与基岩凸起等不良地质体[14]。刘铁华提出了微动技术适用性的量化研究[15]；殷勇等基于波束形成法计算台阵响应函数，探究了排列参数对探测深度和分辨率的影响[16]；

近年来，随着城市地铁建设的发展，城市地下空间探测需求与日俱增，尽管ESPAC法的改进提高了微动技术野外数据采集台站布设的灵活性，但规则的排列方式在复杂的城市地表环境下依然面临巨大的挑战。Bettig和Bard等提出的MSPAC法基于子排列划分思想，实现了任意排列方式空间自相关系数的计算，在城市复杂地表条件下具有广阔的应用前景[17]。为此，本文以实际工程为例，展示MPSAC法处理流程，探究MPSAC法在工程实践中的应用效果。

2 MSPAC法

MSPAC法同样基于Aki的研究成果[18]，根据Aki的研究有如下式成立：

(1)

(2)

其中，θ为波传播方位;φ为台阵对方位。

MSPAC法不像传统SPAC法或ESPAC法必须使用规则的排列方式，如圆形、嵌套三角形等，Bettig基于子排列划分的思想，将所有可能的台站组合按照其间距划分为多个环形子排列，对每一个环形子排列计算其方位平均空间自相关系数。考虑到圆环厚度因素的影响，通过沿径向积分的方式求取平均空间自相关系数：

(3)

式中,r1和r2分别代表圆环内外半径。据此可以计算任意排列空间自相关系数，而圆环的设计原则为圆环内台站组合尽可能多，而圆环厚度尽可能小。

3 工程实例

3.1 地质概况

深圳地铁13号线地表穿越城市闹市区，地面交通流量大，地下管线设施密集，部分区间连续无钻长度超过300 m。地铁建设采用盾构法施工，基岩起伏情况对设备机型选择及投资预算至关重要，而既有钻孔揭示线路下方基岩起伏较大，为提高勘察精度，避免因地质原因引起工程变更，决定在未施钻孔地段开展物探工作。工区内岩层主要包括人工填土层、黏土层、砂岩层，下伏基岩为花岗岩，强、全风化岩分布广泛，厚度变化大，均匀性较差。

3.2 反STA/LTA算法预处理

STA/LTA(Shot Time Averaging/Long Time Averaging)算法用于捕捉地震信号的时间窗[19]，STA越短，对短周期信号捕捉越有效，LTA是用于衡量时间窗内的平均噪声，因此通过调节STA/LTA就可以识别微动记录中的突变信号，而反STA/LTA就是将识别到的异常突变信号舍弃，保留稳态信号。由于城市车辆过往频繁，人文活动较多，微动记录中包含大量瞬时干扰信号，如图1所示，通过合理调节参数，可消除近源干扰信号，提高后续计算结果精度。

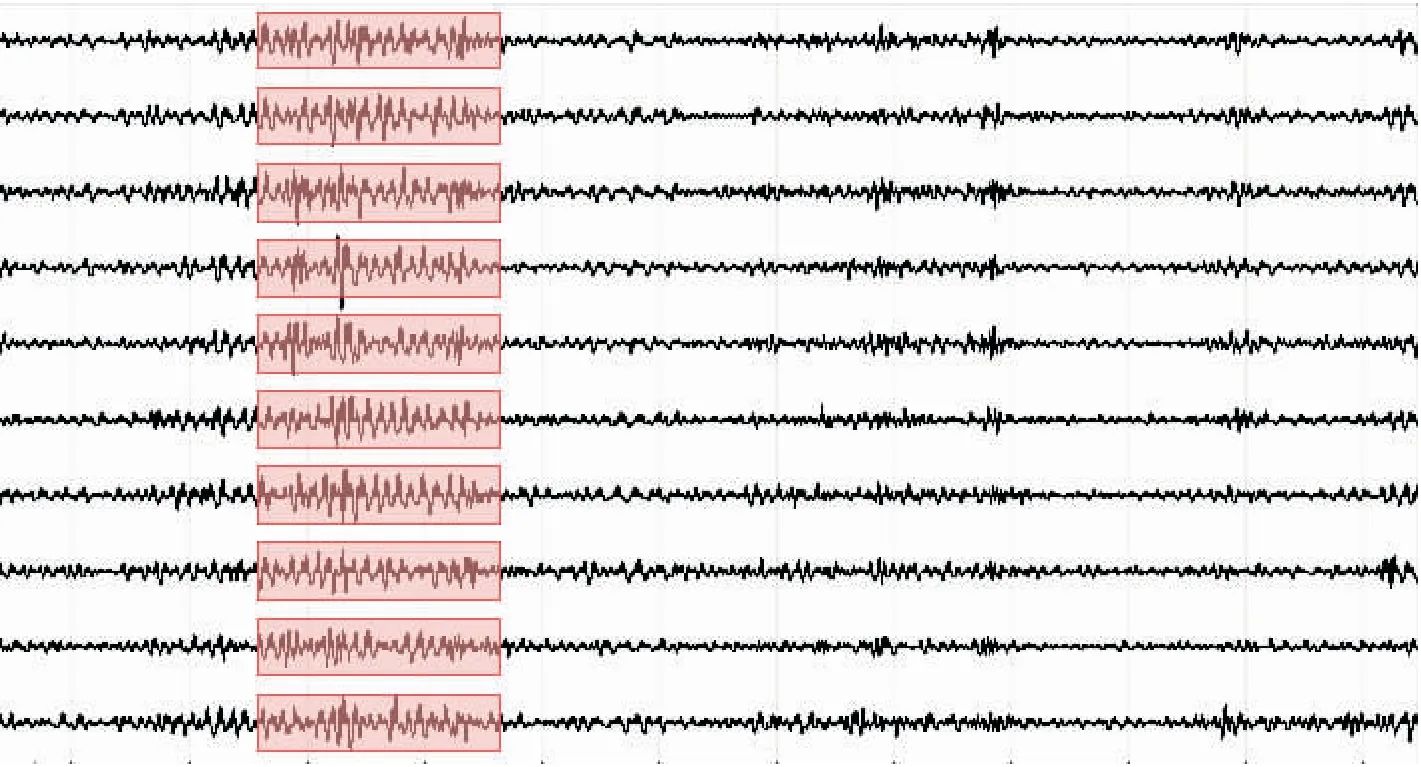
图1 反STA/LTA算法筛选稳态信号Fig.1 Selection of stationary signals by anti-STA/LTA algorithm

3.3 空间自相关系数计算及频散曲线分析

图2为本次MSPAC法空间自相关系数计算圆环设置情况。根据台站组合间距将其划分为4组，分别为2.5～6 m、8～11 m、11～15 m、15～20 m。 图3为4组圆环空间自相关系数计算结果。空间自相关系数是求取频散曲线的基础，Aki通过数值求解零阶贝塞尔函数获得频散曲线，但同一频率可能存在多个相速度满足方程，并且在观测数据有限的情况下解的稳定性和可靠性难以保证；ESPAC法改变策略，采用最小二乘拟合空间自相关系数和零阶贝塞尔函数，再通过数值求解零值的方式获得频散曲线，提高了计算结果的稳定性和可靠性。为进一步提高频散曲线计算的准确度，Bettig利用非线性反演的方式求取频散曲线，通过误差分析评价空间自相关系数数据质量，去除对频散曲线计算负贡献的空间自相关系数。如图4所示，绘制空间自相关系数反演得到的频散曲线能量谱，通过拾取上、下限(图中灰色实线)确定有效频散曲线能量谱范围，并获得如图4所示的空间自相关系数筛选结果。图5中黑色圆点代表经该点计算得到的频散点位于图4约束的频散曲线范围之内，而灰色圆点部分代表经其计算得到的频散曲线点超出约束范围，应当对其舍弃。同样，通过观察不同半径圆环子排列频散曲线计算点特征可以发现，小半径排列对频散曲线高频部分贡献较多，而大半径则对低频信息贡献较多，圆环内台站组合对越多，方位分布越均匀，频散曲线计算质量越好。相较于常规频散曲线求取方式，非线性反演算法提供了更多空间自相关系数和频散曲线关系的细节，有利于优化空间自相关系数曲线，从而获得更为可靠的频散曲线。

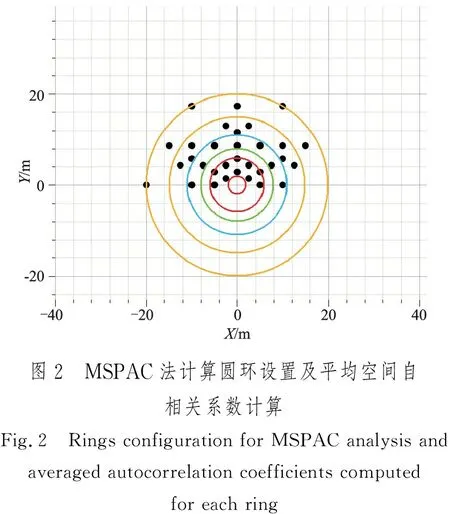
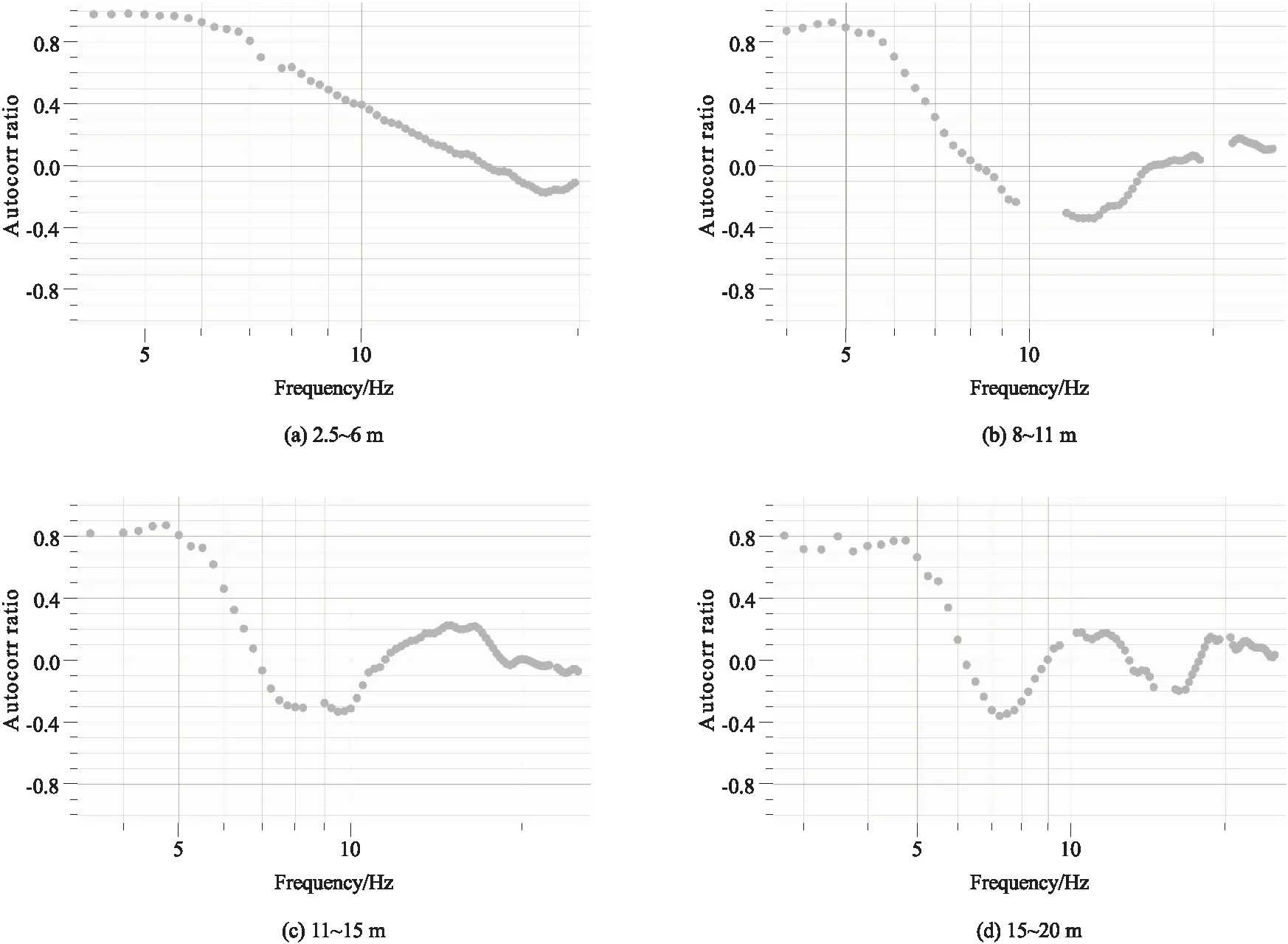
图3 空间自相关系数计算结果Fig.3 Calculation results of spatial autocorrelation coefficient

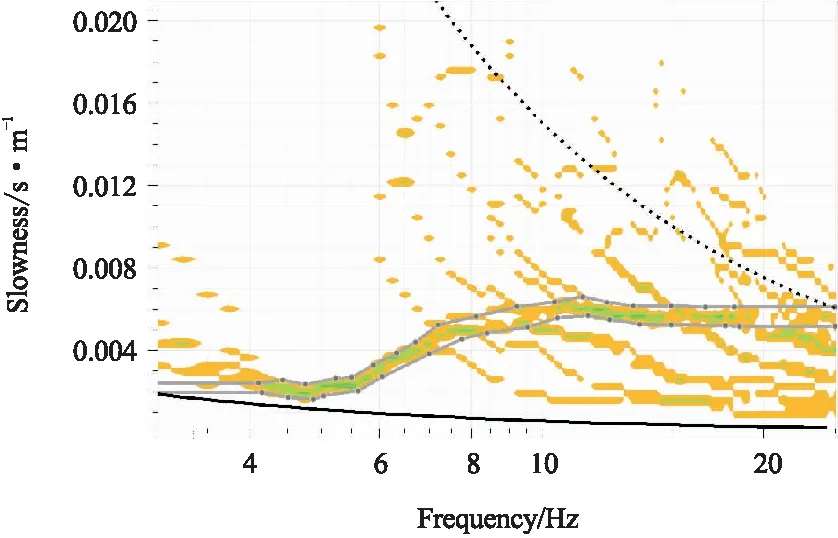
图4 反演频散能量谱Fig.4 Inverted dispersion spectrum

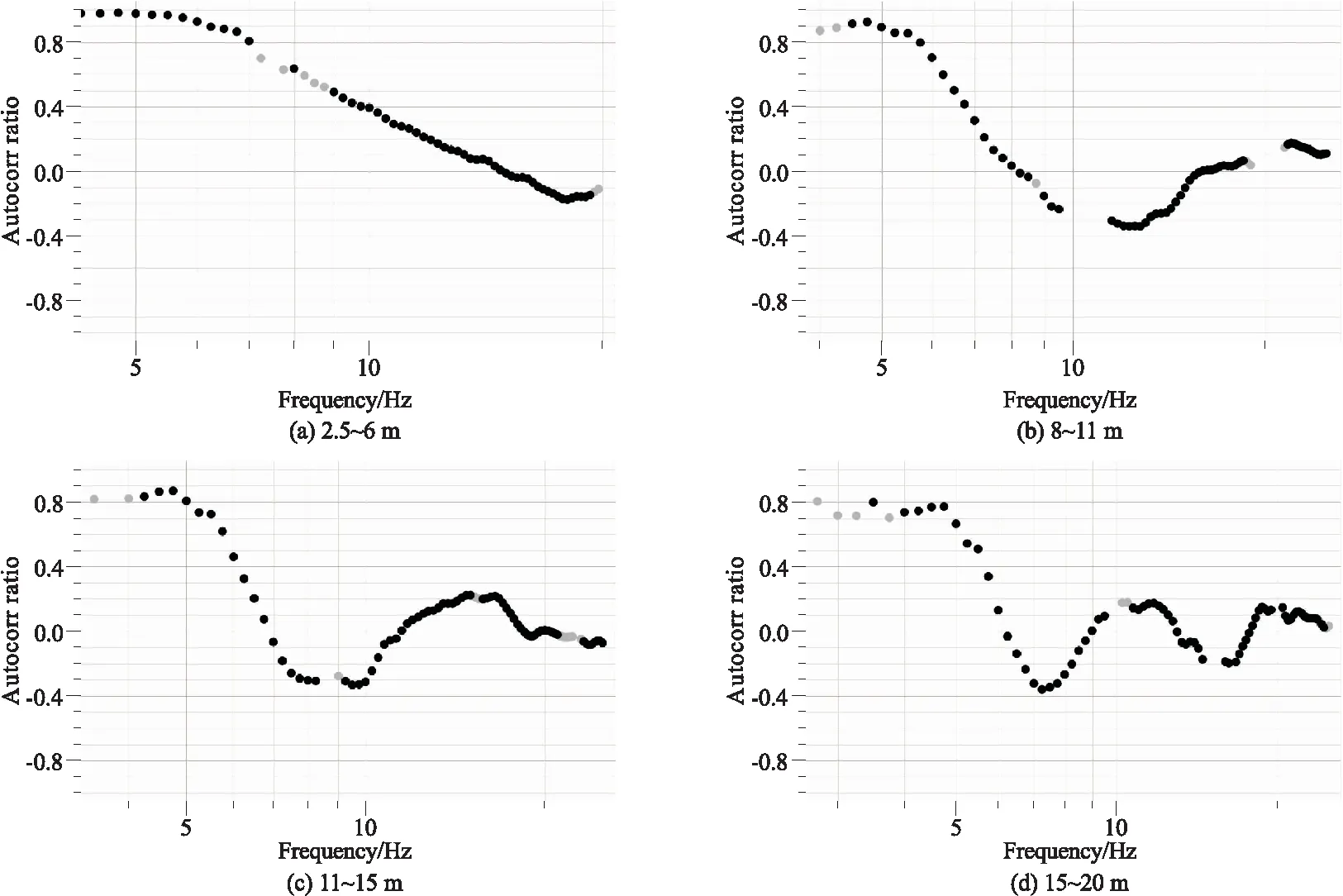
图5 空间自相关系数对频散曲线贡献关系Fig.5 Contribution of spatial autocorrelation to dispersion curves

3.4 地层横波速度结构反演

通常在获得频散曲线后便可以通过最小二乘反演获得地层横波速度结构信息，Marc Wathelet将邻域反演算法应用到空间自相关系数地层横波速度反演中[20,21]。相较于最小二乘算法，邻域反演算法能够深入挖掘模型参数空间，首先初始化地层模型物理参数，给定地层厚度、速度、密度、泊松比等物性参数搜索范围，然后基于模型空间生成大量数值模型，通过正演计算和约束反演误差，获得最终结果。利用空间自相关曲线直接反演地层横波速度信息跳过了频散曲线反演计算，避免了频散曲线计算所引入的误差，并且通过频散曲线约束分析获得了优选后的空间自相关系数曲线，以此为输入进行邻域反演有利于提高反演结果的可靠性。如图6(a)所示为反演模型误差位于4.74 %～4.86 %区间范围的地层横波速度模型，可以看到覆盖层速度分布较为稳定，土石分界位于12～16 m埋深范围，将模型误差取最小值(4.73 %)，获得图6(b)所示为地层横波速度模型，此时土石分界埋深为13.1 m，该测点位置钻孔柱状图揭露土石分界埋深为12.5 m，误差为0.6 m，两者较为吻合。

图6 空间自相关系数邻域反演Fig.6 Vs profile inversion from SPAC curve

3.5 成果解释

图7为物探测线微动反演成果断面图。图中黑色实线为物探解释土石分界线，从图6中可以看到，在里程38 470～38 610段基岩速度整体较高，表明该段基岩结构完整性较好或风化程度低；里程38 610～38 730段基岩速度整体偏低，局部出现低速条带，表明该段基岩结构完整性差或风化程度高。将地质钻孔柱状绘制在微动成果断面对比分析发现，钻孔揭露岩面高程与微动解释岩面高程基本吻合，且基岩风化程度与物探解释一致。表1所示为场地剪切波速度测试资料，从表中可知，全风化花岗岩与土层速度接近难以区分，因此微动成果所揭示岩面为强全风化界面。上述结果表明，基于MSPAC法的微动探测技术能够有效识别岩体性质差异。

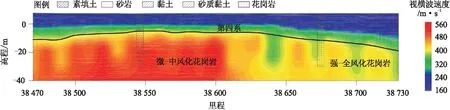
图7 微动探测综合解释断面Fig.7 Comprehensive interpretation profile of microtremor survey

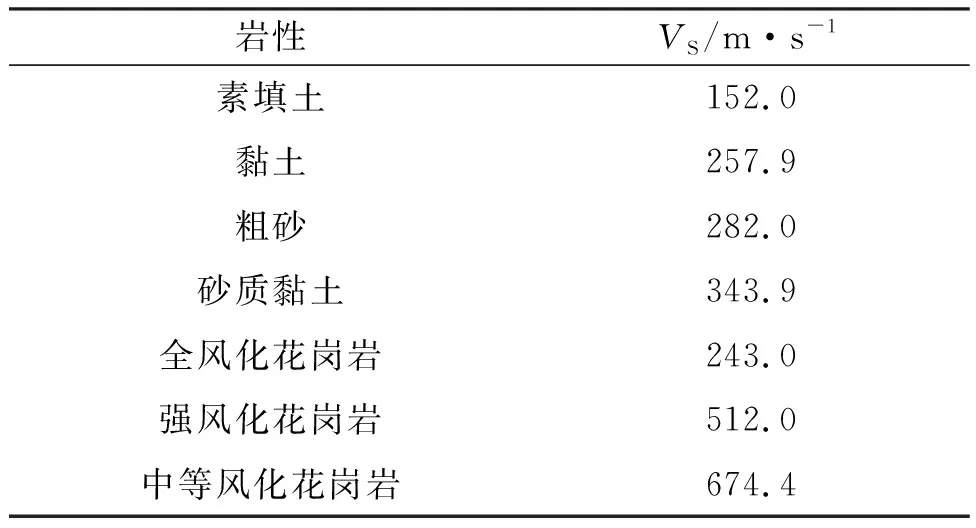
表1 场地剪切波速度测试

4 结 论

本文以实际工程数据为例，探究了MSPAC微动数据处理算法的稳定性和可靠性，具有一定的实践参考价值。MSPAC算法基于子排列划分的思想求取空间自相关系数，虽然观测台站不需要布设成规则的形状，但并不意味着台站布设可以随心所欲。为了获得稳定、可靠的计算结果，观测台站布设应当尽可能均匀覆盖各个方位，并且保证排列长度能够满足勘探深度要求。实践中应当结合地表条件，合理放置观测台站，对于因建筑阻挡无法放置的，可在反方向布设台站，弥补方位数据的缺失。由于MSPAC法需要划分子排列，若子排列内台站组合对较少，势必造成计算结果出现较大误差或稳定性较差，因此相较于规则排列方式，MSPAC法野外工作需要投入更多的观测台站。

基于频散曲线反演地层横波速度结构发展较为成熟，本文介绍了利用空间自相关系数曲线通过邻域算法直接反演地层横波速度结构的方法，“一步式”反演跳过了求取频散曲线过程中引入的不确定性误差，同时将空间自相关系数曲线反演频散曲线作为评价空间自相关系数计算质量的手段，筛选反演时参与运算的空间自相关系数，达到进一步提高反演稳定性和准确度的目的。基于邻域搜索算法能够进行反演模型误差分析，由于物探多解性的问题，对反演结果引入误差分析有利于正确认识和评价反演结果质量，更具有实践指导意义。