基于激发极化法的隧道超前地质预报三维正反演研究

吴奎锋，王福亮，丁建芳，赵香玲,寇春阳

(1.中铁西南科学研究院有限公司，四川 成都 611731；2.四川绵九高速公路有限责任公司，四川 绵阳 621700)

1 引 言

随着我国交通设施建设的加快，将会修建更多的隧道工程，含水构造超前探测是保障隧道施工安全的重要环节，在隧道含水体的超前预报物探方法中，应用最为广泛的是地震波反射法(Tunnel Seismic Prediction,TSP)[1]、电磁波反射法、直流电法[2-4]、瞬变电磁法和复频电导法(Complex Frequency Conductivity,CFC)[5,6]。激发极化法因受隧道环境限制，相对于其他方法，在隧道中的应用研究较晚；德国Geohydrauuc Data公司推出了一种全新聚焦电流频率域激电隧道超前预报方法(Bore-tunning Electrical Ahead Monitoring,BEAM)[7]，该技术应用在TBM环境下，通过探测仪器、传感器与TBM装备集成，实现了自动测量，它是一种充分利用电流同性相斥的原理，通过外围环状电极的频域诱导极化特征来探测掌子面前方的地质异常体，这种方法在欧洲许多国家得到应用，但在国内报道或应用相对较少；山东大学李术才院士团队[8,9]研发的以激发极化法为理论基础的隧道超前探测系统，其从视电阻率值和半衰时差着手，通过三维数据反演预测前方含水异常体，该方法在国内部分隧道中得到应用，并取得了一定的成果。

前人的研究工作取得了阶段性的成果，但也存在如下问题：一是激发极化法三维反演时，大多采用的反演思路均先进行电阻率参数反演，再依据电阻率反演结果进行极化率反演，致使反演结果过多依赖于电阻率反演[10]；二是在进行电阻率和极化率参数反演时，未考虑两种物性参数之间的耦合关系。针对上述问题，本文对反演目标函数进行优化，采用有限内存拟牛顿法设计快速有效的自动反演方法，反演过程中同时迭代更新电阻率和极化率两种物性参数；并依据电阻率和极化率之间的结构耦合关系，引入交叉梯度函数约束两种参数反演[11]，提高反演解译的精度与准确性，最后通过理论模型合成数据验证正反演算法的可行性和有效性。

2 激发极化法探测理论及隧道环境探测装置选择

激发极化法超前探测是以岩矿石的激发极化效应为基础，通过观测隧道位置的视电阻率和视极化率变化规律来探测掌子面前方地质情况的一种地质预报方法[12-14]，由于节理裂隙、断层破碎带、溶洞等易富水地质构造的富水量、分布规模等对围岩的激发极化效应影响较大，依据激发极化法探测富水地质构造具有天然的优势，地层含水量越大，地层激电效应越强，其极化电场越明显、越容易探测，进而通过分析获取掌子面前方含水地层的位置和规模等情况[15]。

激发极化法在隧道地质预报探测中，针对隧道全空间环境，应对探测布极、聚焦、供电、数据处理、解释等技术进行改进，方能实现隧道超前预报的目的。传统激发极化法探测装置有：对称四级测深装置、中间梯度装置、固定电源排列装置、联合剖面装置等；由于隧道环境下可布极空间有限，测线只能沿隧道洞身方向布设；中间梯度装置、对称四级装置在隧道环境下无法布设；联合剖面装置沿隧道洞身方向移动电极，主要观测隧道洞身段旁侧地质信息，而隧道超前地质预报主要是探测掌子面前方地质信息，因此适合隧道环境探测装置只能选择定源排列装置。

定源排列装置可分为定源二级装置(AM)和定源三级装置(AMN)[16,17]，定源三级装置相较于定源二级装置，具有纵向分辨率高，受旁侧地质信息影响小的特点，本文选用定源三级装置作为观测装置[18]，测线沿隧道走向布置在隧道底板或边墙，供电点源A极固定在掌子面，B极放置在无穷远处，测量电极M、N沿测线移动以采集数据，在隧道底板和左右边墙上布置多条测线，一方面多条测线数据之间可相互校核，提高数据的可信度，另一方面增加了观测数据量，有利于抑制反演的多解性，每条测线可反映不同位置的异常信息，有利于实现掌子面前方异常体的三维成像[19]。

3 三维正演数值模拟

3.1 正演理论

隧道施工激发极化法三维正演数值模拟就是在已知围岩电阻率和极化率分布的情况下，求解隧道腔体接收器位置的视电阻率和视极化率，三维介质正演问题无解析解，只能通过数值模拟方法来进行求解，正演从点电源微分方程出发，采用矩形网格离散地下介质，并在边界处设置边界条件，最后求解大型稀疏矩阵线性方程组。含隧道腔体地质模型如图1所示。点电源A位于隧道掌子面处，电性参数Ω1介质中存在电性参数为Ω2的不均匀体，Γ∞表示无穷远处边界，Γ表示两种介质分界面。

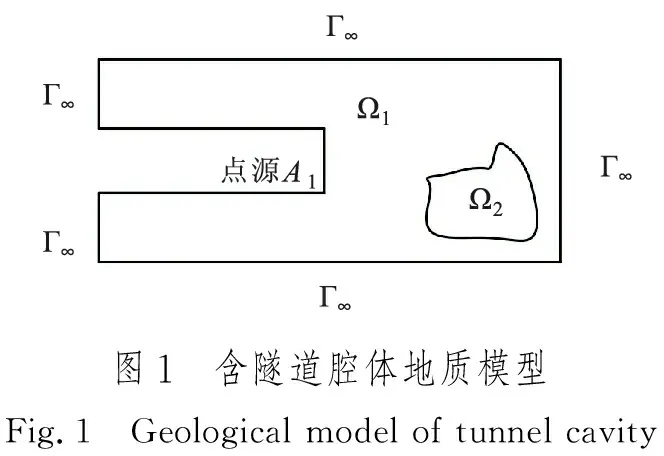
对于一次电位求解，在均匀全空间模型中，若忽略地表反射界面对地下介质电场的影响或点电源距离地表足够远，则一次电位可表示为：

(1)

式中，u0为一次电位，单位为V;I为电流强度，单位为A;r为场点到源点的距离，单位为m;σ0为均匀全空间电导率，单位为S/m。对于二次电位的求解，采用异常电位法求解含隧道腔体的全空间三维点源场[20]，二次电位所满足的微分方程如下：

∇·(σ∇u)=-∇·[(σ-σ0)∇u0]

(2)

式中，u为二次电位，单位为V;σ为异常体电导率，单位为S/m。离散区域边界可分为内边界和外边界，在计算过程中内边界条件会自动满足，外边界是指网格剖分区域模拟无穷远处的边界及地表与空气界面，在这些边界处采用第三类边界条件。

(3)

式中，n为边界外法线向量;n1和n2分别为Ω1和Ω2的外法线方向;u1和u2分别为Ω1和Ω2的电位，单位为V。

考虑到计算精度和计算效率，选取有限差分法进行数值模拟，有限差分法解直流电法正演问题时，首先需要离散偏微分方程式(2)，再通过数值方法求解离散后的方程，从而得到地下的电位分布。直流电法正演方程可表示为如下线性方程组：

Ku=-(K-K0)u0

(4)

其中，K是一个大型稀疏对称正定的系数矩阵;K0为一次电位全空间系数矩阵;u是剖分区域各节点的电位向量;u0为均匀全空间一次电位。

采用稳定双共轭梯度法(BICGSTAB法)求解式(4)线性方程组，即可得到所有网格节点处的二次电位u。通过整理电位或者电位差，即可得到视电阻率参数：

(5)

式中，ρa为视电阻率，单位为Ω·m;K为装置系数;Um为接收点M的电位(单接收极)，单位为V;ΔUmn为接收电极M和N之间的电位差，单位为V。

激发极化法正演包含两部分内容，即无激电效应所产生的场和含激电效应产生的场的叠加，在进行激发极化法正演模拟时，需进行两次直流电法正演，将式(2)中电导率σ替换成带激电效应的电导率：

ση=σ(1-η)

(6)

其中，η是地下地质体的极化率，单位为C·m2/V;ση表示带激电效应的电导率，单位为S/m。

利用直流电法的正演方法，先正演计算不含激电效应的视电阻率，再正演计算含激电效应的视电阻率，最后得到视极化率：

(7)

其中，ηa是地下地质体的视极化率，单位为C·m2/V;ρη和ρ分别为含激电效应和不含激电效应接收点处的视电阻率，单位为Ω·m。

3.2 隧道腔体影响分析

在全空间模型中，植入一高阻体来模拟隧道腔体，模型参数如下：全空间默认电阻率为1 000 Ω·m，隧道腔体默认电阻率为1.0×106Ω·m；掌子面前方为均匀介质；采用定源三极装置，点源A位于掌子面，接收极M、N沿隧底均匀布极，极距MN=3 m，收发距AO从3 m至117 m,以3 m为点距均匀增大。通过正演计算即可得到图2中纯隧道腔体的视电阻率响应曲线和纯隧道腔体的视极化率响应曲线。

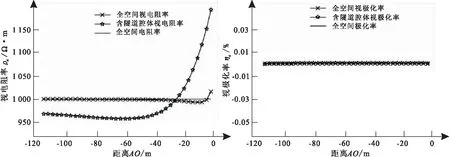
图2 纯隧道腔体正演响应对比曲线Fig.2 Contrastive curve of forward response of pure tunnel cavity

对比视电阻率响应曲线和视极化率响应曲线可得出如下结论：

1)均匀全空间视电阻率响应基本与围岩电阻率一致，在收发距较小时略有所偏差，为场源效应所致。

2)存在隧道腔体时，视电阻率曲线受隧道腔体影响严重，视电阻率数据无法反映围岩的真实电阻率；视极化率曲线不受隧道腔体影响，视极化率数据能反映围岩的真实极化率。

3.3 正演模型算例

隧道施工中，富水溶洞是常见的致灾地质构造，设定隧道前方为电性介质均匀的全空间，默认为电阻率为1 000 Ω·m，在均匀空间中植入低电阻率高极化率异常体，如图3所示，异常体模型参数如下：电阻率为10 Ω·m，极化率为20 %，来模拟隧道中富水溶洞构造。

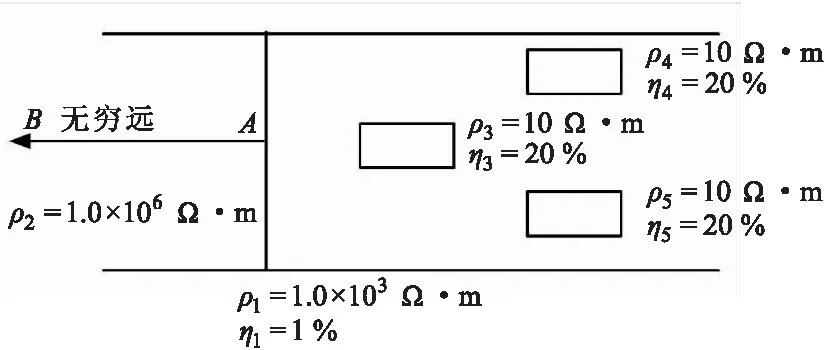
图3 富水溶洞模型Fig.3 Water-rich karst cave model

在点电源A的激发下，通过正演计算出所有节点的视电阻率和视极化率，选取其中一剖面(Z=0 m)，其视电阻率和视极化率响应如图4所示。

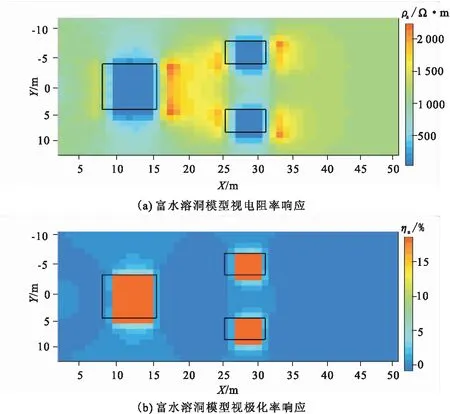
图4 富水溶洞模型正演响应Fig.4 Forward response of water-rich karst cave model

从视电阻率响应曲线和视极化率响应可以看出，视电阻率及视极化率对三个异常体都有明显的响应，且对隧道开挖方向(X方向)分辨率较高；视电阻率响应存在局部的旁侧效应，出现高阻假异常，视极化率响应不存在旁侧效应。

4 三维反演数值模拟

4.1 反演理论

从视电阻率和视极化率曲线很难直观得到异常体的信息，需要借助反演技术对异常体进行解释，地球物理反演是依据观测数据去反推地球物理模型的过程，在三维反演中，比较常见的反演方法有最小二乘法、非线性共轭梯度法(Non-linear Conjugate Gradient, NLCG)、OCCAM法、有限内存拟牛顿法(L-BFGS)等。

表1 不同反演方法优缺点对比

本文选用有限内存拟牛顿法(L—BFGS)实现电阻率和极化率双参数反演[11]。三维激发极化法反演目标函数可以表示为：

(8)

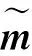
Wd=diag{1/σ1,1/σ2,...1/σj,...1/σm}

(9)

其中，σj为第j个观测数据的误差。引入数据协方差矩阵主要有两个目的：

1)不同偏移距时，对数据有一定的归一化作用，可以有效地平衡不同偏移距的观测数据，以达到稳定反演的效果。

2)数据质量参差不齐时，可以降低质量较差观测数据的权重，避免反演过度的去拟合质量较差的数据。

在多参数反演中，介质的物性变化规律可以用一个梯度矢量进行描述，既包含变化数值的信息，又含有方向信息。对于不同物性参数的反演，提出了一种基于交叉梯度约束的多参数反演算法，在反演的目标函数中加入交叉梯度项来进行模型参数的耦合约束。在模型更新过程中，兼顾数据拟合、模型正则化、不同的物性参数等信息同步迭代下去，直到达到反演终止条件。

三维模型交叉梯度函数的定义如下：

(10)

式中，mσ代表电导率参数；mη代表极化率参数。交叉梯度函数有以下几点性质：

1)两种电性参数进行交叉梯度计算时，当任意一种电性参数不发生变化时，交叉梯度值为零。

2)交叉梯度值不受电性参数数值改变幅度的影响。

3)交叉梯度值与两种电性参数结构耦合性相关，物性参数变化方向不同时，交叉梯度值不为零，结构越相似，交叉梯度数值越小。

在式(8)引入交叉梯度项后的目标函数：

(11)

对应的电导率参数目标函数梯度可表示为：

(12)

对应的极化率参数目标函数梯度可表示为：

(13)

交叉梯度项关于电导率的偏导数只与极化率参数有关，关于极化率参数的偏导数只与电导率有关，目标函数梯度直接影响海森矩阵的计算及模型更新的步长及方向等因素，引入交叉梯度项，可以让两种参数在反演过程中结构有意识地去趋于一致。

有限内存拟牛顿法(L—BFGS)主要思路是采用当前迭代之前几次的目标函数梯度去逼近当前迭代过程中的海森矩阵逆，L—BFGS逼近海森矩阵大致的流程如下所示：

1)选择好双参数初始模型m0，给出反演过程中最大的迭代次数IterMax，并给出反演迭代最小拟合差Rms；

3)设定好初始步长，在初始步长的基础上进行一维线搜索，寻求相对最佳的步长α：

mk+1=mk+αpk

(14)

4)计算更新后模型的拟合差是否达到给定的精度，若达到精度则终止反演，若迭代次数达到上限也终止反演，否则继续回到第二步进行循环。

4.2 理论合成数据反演算例

在进行激发极化法超前探测前需明确该方法的有效探测范围，实际工作中，观测数据信噪比大于3时方可视为有效数据，激发极化法探测中最大误差水平为5 %，即超过15 %的观测异常数据方可视为有效数据，以视电阻率数据为例，视电阻率的异常幅度是指含水体存在时的视电阻率数据极小值相对于均匀围岩情况下的视电阻率数据的变化程度，表示式如下：

(15)

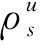
均匀全空间围岩电阻率默认为1 000 Ω·m，隧道腔体电阻率默认为1.0×106Ω·m，假定隧道宽12m，高12m；在均匀空间中植入低阻高极化异常体，参数如下：电阻率为10 Ω·m，极化率为20 %，长8 m，宽8 m，高6 m，来模拟隧道中富水溶洞构造，如图5所示。

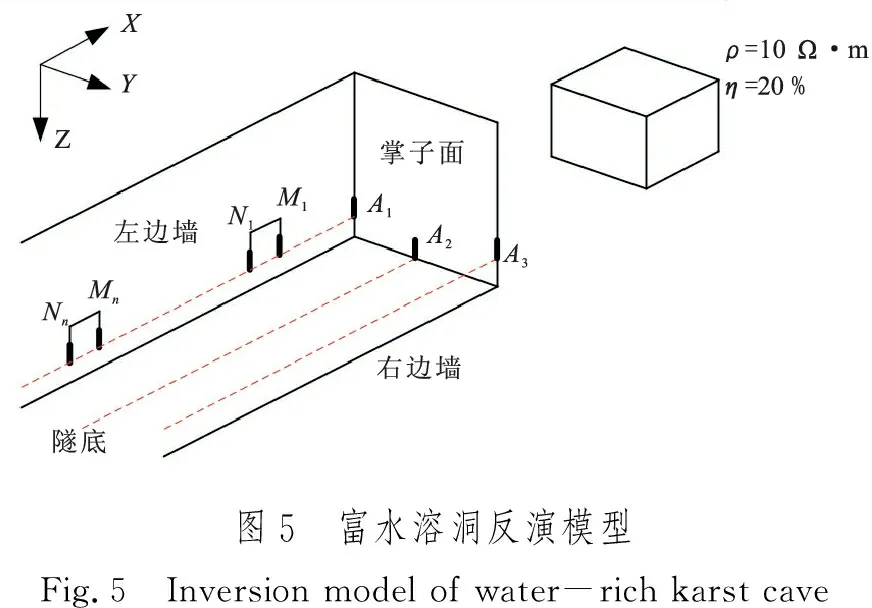
数据采集采用定源三极装置，点电源A位于掌子面处，沿隧道左、右边墙、隧底分别布置测线，接收极距MN=3.0 m，收发距AO=3～117 m，通过正演模拟计算观测数据，其视电阻率及视极化率响应如图6所示。

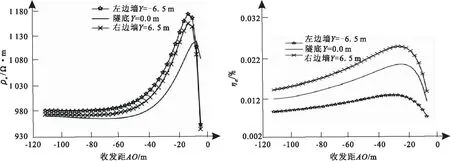
图6 纯隧道腔体正演响应对比曲线Fig.6 Contrast curve of forward response of pure tunnel cavity

对视电阻率和视极化率数据分别附加5 %误差，初始模型设定为电阻率1.0×106Ω·m均匀全空间，分别进行双参数同步反演和交叉梯度约束反演计算，反演结果取YZ剖面(X=12 m)及XZ剖面(Y=6 m)，如图所示。

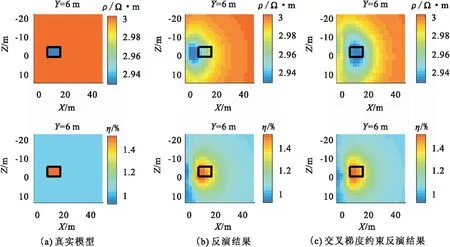
图7 XZ剖面(Y=6 m)模型成果Fig.7 XZ profile (Y=6 m) model result drawing

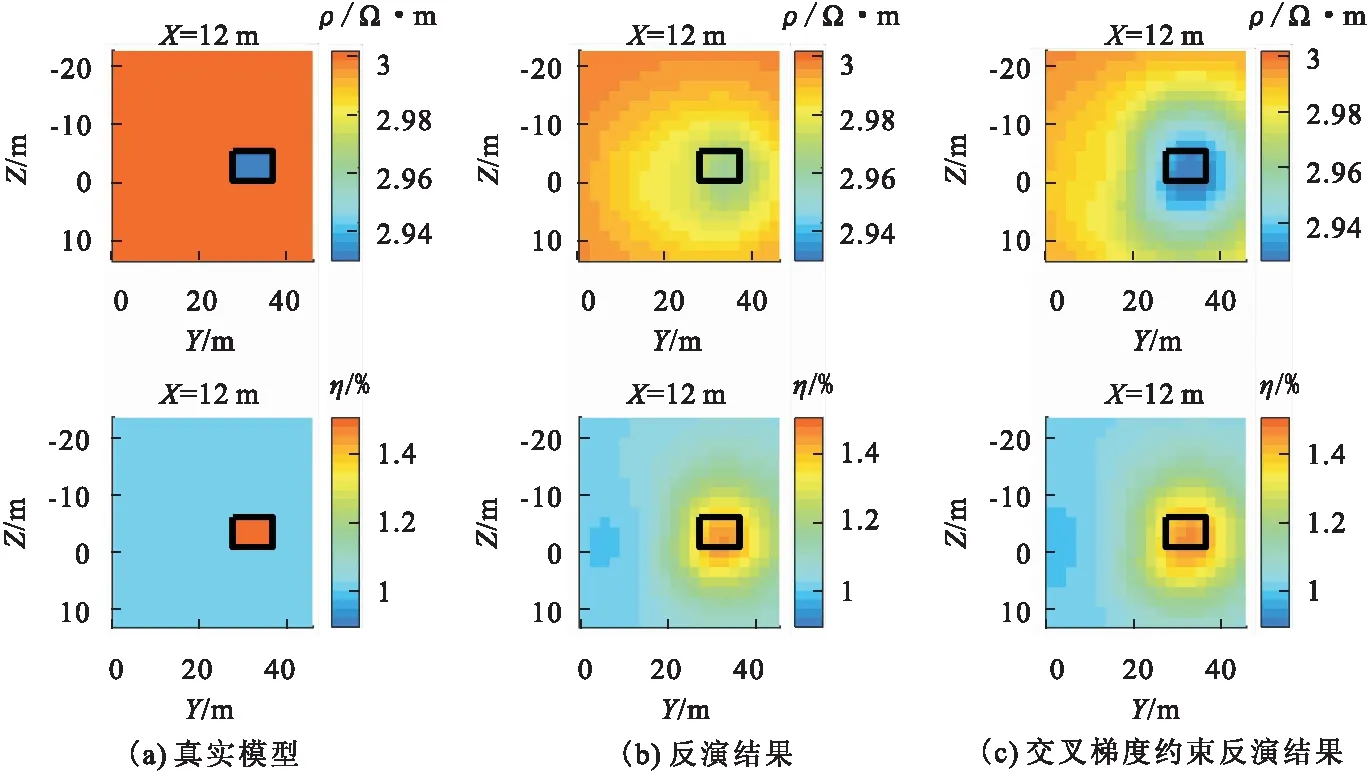
图8 YZ剖面(X=12 m)模型成果Fig.8 YZ profile (X=12 m) model result drawing

通过电阻率和极化率反演成果图可得出：

1)同步反演电阻率和极化率时，电阻率反演结果受测线布置影响较大，深度信息缺失严重；极化率反演受测线布置影响较小，能大致圈定异常体形态。

2)引入交叉梯度约束反演电阻率和极化率时，可有效消除测线对电阻率反演的影响，电阻率和极化率两种物性参数相互约束，均能大致圈定异常体形态。

3)隧道环境下观测数据信息量存在局限性，测线主要包含X方向(隧道开挖方向)深度信息，对Y方向和Y方向深度信息缺失较大，导致X方向(隧道开挖方向)异常体分辨率较高，Y方向和Z方向分辨率较低。

5 结 论

本文以实现隧道环境下激发极化法三维正演和反演算法为核心任务，取得如下主要结论：

1)通过正演对隧道腔体影响进行分析，得出视电阻率曲线受隧道腔体影响严重，视极化率曲线不受隧道腔体影响。

2)推导电阻率和极化率对应的目标函数梯度公式，依据有限内存拟牛顿法实现电阻率和极化率同步反演，相对于传统电阻率和极化率分布反演，提高了反演计算效率。

3)基于不同物性参数结构耦合性，反演过程中引入交叉梯度函数约束电阻率和极化率，可有效提高反演精度。

4)实际探测中地质条件更为复杂，数据干扰更为严重，沿隧道腔体布设测线得到的数据局限性较大，可优化布极方式，也可通过综合超前地质预报获得更多的先验信息，提高超前探测精度。