反应位移法Ⅰ计算精度影响因素分析

孙昕宇，范 进，丁建国，黄宏坤

南京理工大学，江苏 南京 210094

《地下结构抗震设计标准》（GBT 51336—2018）[1]对反应位移法Ⅰ中部分因素如地基弹簧间距、地基弹簧刚度确定方法、惯性力施加方法等给出多种确定方法。王文晖[2]表明，经验公式求地基弹簧刚度用于反应位移法存在一定误差；对此，王璐[3]、林皋[4]、王文沛等[5]给出了不同的地基弹簧刚度系数计算方法，认为惯性力较结构周围剪力对结构内力影响小；许成顺等[6]提出不同惯性力施加方法对反应位移法计算精度存在影响；王立新[7]、叶丹[8]表明反应位移法用于地下结构地震响应分析存在一定误差，这源于地基弹簧对周围岩土体的简化。针对上述问题，文章分析了地基弹簧间距、地基弹簧刚度确定方法和惯性力施加方法等因素对计算结果的影响及影响规律。

1 岩体隧道混凝土结构二维时程分析法及反应位移法Ⅰ建模

计算模型简化自某工程，围岩为泥灰岩，深度为50m，隧道埋深21m，隧道纵向长度为20m，采用C40混凝土。建模采用ABAQUS软件，采用反应位移法时，考虑土层相对位移、结构惯性力和结构周围剪力。相对位移通过地基弹簧以静荷载的形式作用在结构上；地基弹簧通过弹簧、阻尼器模块设置，约束远离结构端的多余自由度，在需要施加相对位移的位置设置相应边界条件；剪应力使用表面荷载设置；惯性力施加需将隧道模型划分为4个区域，在每个区域的质心处施加集中力，或在结构上设刚性杆，在结构的形心施加惯性力；使用载荷模块添加结构重力、围岩的上覆荷载和围岩对结构侧壁的压力[9]。

2 反应位移法Ⅰ计算精度的影响因素

对比地基弹簧间距因素，分别在反应位移法Ⅰ模型每个侧面设置2、3、4组地基弹簧，对应地基弹簧间距分别为3000mm、2000mm、1600mm，对应模型记为模型1、模型2、模型3；对比地基弹簧刚度确定方法因素，依据每侧3组弹簧模型，按静力有限元方法确定弹簧刚度，对应模型记为模型4；对比不同的惯性力施加方法因素，依据每侧3组弹簧模型，改变拆分方法，对应模型记为模型5、模型6。

2.1 时程分析法计算结果

时程分析法最大加速度时刻结构最大主应力云图如图1所示。

图1 时程分析法隧道截面最大主应力云图和最大主应变云图（单位：MPa）

2.2 地基弹簧间距

改变地基弹簧间距，模型1、模型3最大主应力与最大主应变云图如图2所示。

图2 反应位移法隧道截面最大主应力云图和最大主应变云图（单位：MPa）

弹簧间距对结构应力应变的分布及具体应力应变值影响不大。弹簧间距减小，拉应力增大、压应力减小；除隧道两侧地基弹簧附近和底部纵横交接处存在相对较大应变，整体表现为一个较小的压应变，应变值较时程分析法大。

反应位移法得到的结构地震响应接近时程分析法结果，也存在差异：除隧道顶部外，隧道应力更多表现为拉应力。反应位移法求得的隧道应力值较时程分析法更大；反应位移法不能很好地反映隧道结构上的拉应变分布且压应变值计算结果大于时程分析法。

反应位移法压力计算结果与时程分析法较吻合。左侧墙压力值与时程分析法中对应数值差距较大，这与时程分析法和反应位移法隧道模型周围分别设置围岩与地基弹簧的不同边界条件有关。以顶部、底部和右侧墙压力值为误差分析指标，指标值及误差分析如表1、表2所示。

表1 反应位移法隧道内侧表面压力合力值 单位：N

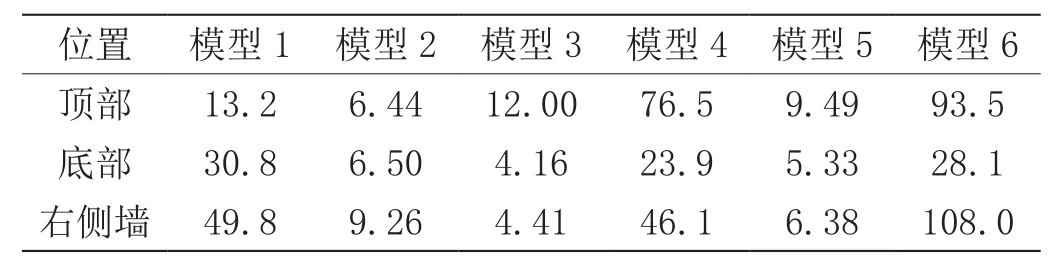
表2 反应位移法与时程分析法计算误差比较 单位：%

对比可知，反应位移法计算精度基本表现为随地基弹簧间距的减小而逐渐精确，最小误差为4.41%。

2.3 地基弹簧刚度确定方法

采用模型4对应的方法对结构应力的分布有明显影响，对应力、应变分布与应变值影响不大。最大主应力分布比规范方法更接近时程分析法结果，应力更多表现为拉应力，在隧道模型内部表面的应力分布规律、应力值更吻合时程分析法结果，应变值整体表现为一个大于时程分析法的小应变。对比可知，采用规范简化公式确定的地基弹簧计算精度更高，最小误差为6.5%。

2.4 惯性力施加方法

改变惯性力施加方法，模型6最大主应力与最大主应变云图如图3所示。

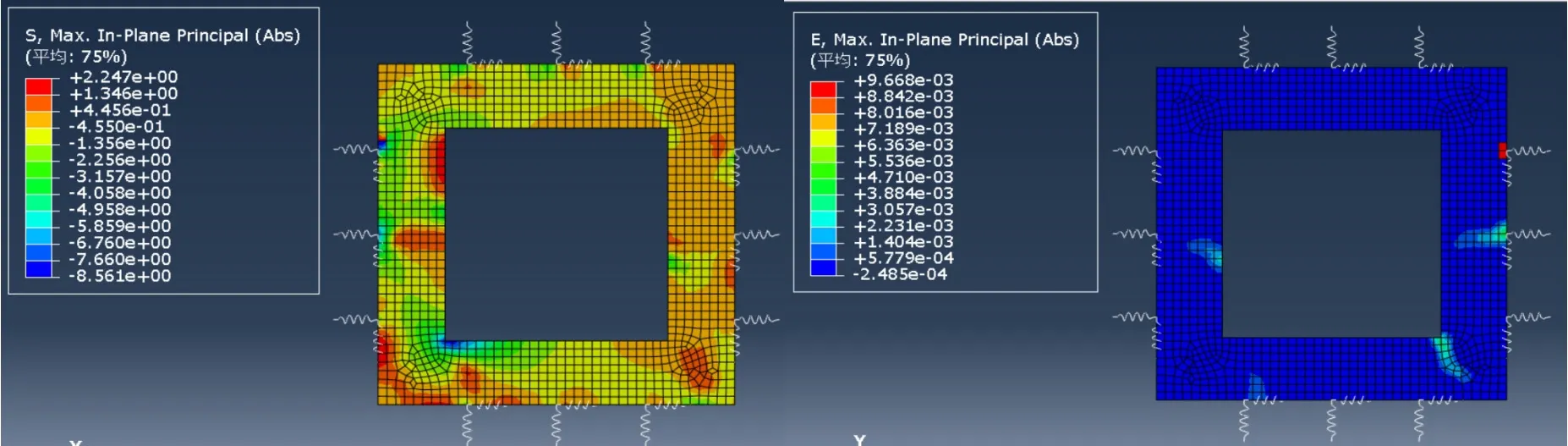
图3 反应位移法隧道截面最大主应力云图和最大主应变云图（单位：MPa）

不同方法对计算结果的影响不大，通过刚性杆传力施加惯性力的方法在隧道结构右侧墙的应力计算结果更接近时程分析法。模型5、模型6应变表现为一个大于时程分析法的小应变。对比可知，将模型拆解分别施加惯性力的方法计算精度更高，最小误差为5.33%。

2.5 最大主应力值比较

选取最大主拉应力值作为误差分析指标，分析结果如表3所示。

表3 反应位移法各模型最大主拉应力及与时程分析法误差

就最大主拉应力指标而言，缩小地基弹簧间距，有效控制误差，间距减少1400mm，误差减少33.59%；规范方法较时程分析法的弹簧刚度确定方法，反应位移法地下结构地震响应值误差偏差14.07%，但需综合考虑应力分布规律；不同结构拆分方式施加惯性力对精度影响不大，误差小于10%，设刚性杆在结构形心施加惯性力精度更高。

3 结论

（1）地基弹簧间距对结构的地震响应应力分布规律影响不大，主要影响结构地震响应中的各项力学指标值。随地基弹簧间距的减小，反应位移法Ⅰ的计算结果更接近于时程分析法结果。就隧道模型内侧表面压力值和最大主拉应力值指标而言，隧道模型每侧设置4组地基弹簧计算误差最小，对应的最小误差分别为4.41%和61.58%。

（2）地基弹簧刚度确定方法主要影响结构的地震响应应力分布规律，使用时程分析法计算得到的地基弹簧刚度用于反应位移法Ⅰ可以获得更接近时程分析法结果，但结构地震响应的具体力学指标值误差增大。

（3）采用增设刚性杆传力在结构的形心施加惯性力的方法，得到的结构地震响应应力分布规律与时程分析法计算结果吻合得更好；采用结构拆分按各部分最大加速度计算惯性力施加惯性力的方法，得到的结构地震响应力学指标误差更小，若以隧道模型内侧表面压力为指标，最小误差可达5.33%。