基于Mindlin 理论新型杯形复合超声变幅杆的设计与研究
朱佳,袁金霖,高雨婷,张宁宁
(渭南师范学院物理与电气工程学院,陕西渭南,714099)
0 引言
超声辅助加工已被广泛应用于高性能合金、复合材料、硬脆材料等难加工材料的高效精密加工[1]。超声振动系统的核心组成部分是超声变幅杆,因此对超声变幅杆的设计和研究至关重要。在变幅杆设计时当加工工具质量较大,应对超声变幅杆和工具杆进行一体化设计[2]。杯型工具的尺寸和质量较大,其固有振动频率、振动模态等很难满足超声加工要求,需把杯型工具看作是超声振动系统的非谐振动单元进行整体设计[3-7]。文献[8]对超声珩磨声学系统中圆盘的进行研究分析。文献[9]研究了用于超声焊接的超声变幅杆和类杯型工具的设计。文献[10-12]对超声变幅杆与薄圆盘基底的杯型工具进行设计研究。以上文献所设计的都是单一变幅杆与薄圆盘、杯型工具组成的振动系统。特别在高频大功率声辐射条件下,薄盘的机械强度不能满足要求,而Mindlin厚板理论不仅兼容薄板理论且计算精度更高。本文基于Mindlin 中厚板弯曲振动理论和耦合振动理论,设计了一种由三段复合变幅杆、中厚圆盘、大尺寸圆筒组成的新型杯形工具复合变幅杆。对所设计的变幅杆进行数值计算和有限元分析,研究了各几何参量对杯形工具复合变幅杆谐振频率的影响,并通过实验进行测试,研究结果可为超声辅助加工技术特别是硬脆材料曲面高精度加工提供了一种新型超声变幅杆。
1 新型杯形工具复合变幅杆的理论设计
新型杯形工具复合变幅杆是由三段复合变幅杆、中厚圆板、大尺寸圆筒三部分组成,其数学模型结构如图1 所示。主要分为三部分:第一部分为三段圆锥形复合变幅杆,第一段半径为 R1,长度为l1,第二段圆锥形杆长度为l2,第三段半径为R2;第二部分为厚圆板,半径为b,厚度为e;第三部分为大尺寸圆管,内半径为a,长度为h。
1.1 厚圆盘的Mindlin 弯曲振动理论设计
在实际应用中常常用到厚径比大于0.2 小于0.5的中厚板,Mindlin 厚板理论更为精确。简支边界条件下弯曲振动厚圆盘的弯矩和横向剪切力都为 0,可得共振频率方程为[13]:
式中H=Eh3/12(1−ν2),k2=π/12.ρ,ω,H分别为圆环板的密度、角频率、弯曲刚度常数,G 为剪切模量,,R S 为转动惯量和横向剪切变形的影响,ν 为泊松比。
1.2 大尺寸圆筒耦合理论设计
当大尺寸圆筒纵向振动时,由于泊松效应会产生径向振动,是一个复杂的三维纵径耦合振动,解析解很难得到。为简化分析,引入等效弹性常数和等效机械耦合系数将其振动等效成纵向和径向振动。在忽略剪切力和应变的基础上根据圆筒的边界条件可得其纵径耦合振动频率方程[14]:
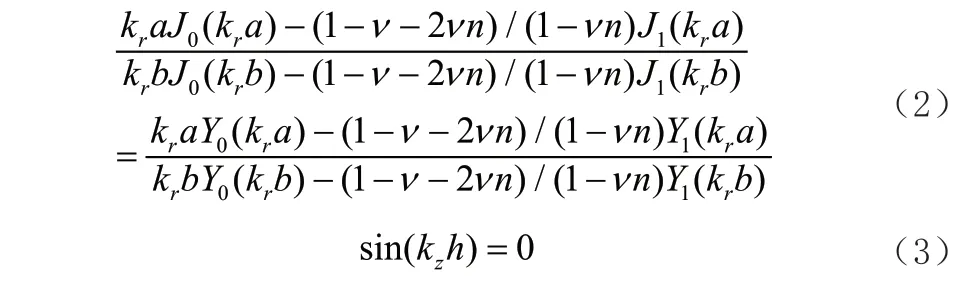
式中kr和kz分别为等效径向和等效纵向波数,n 为等效机械耦合系数,a、b 分别为圆筒内径和外径,J0(kra),J1(kra),Y0(kra),Y Y1(kra)都是贝塞尔函数。圆筒纵径耦合振动的材料参数、几何参数、谐振频率之间的相互关系由式(2)和式(4)决定。
1.3 圆锥复合变幅杆理论设计
前后两段等长的圆锥复合变幅杆振动性能较好。通过传输矩阵法便可求得圆锥复合变幅杆频率方程为[15]:
式中:l1=l3为三段复合变幅杆大小段的长度;l2为过渡段长度;圆锥段截面变化系数
2 新型杯形复合超声变幅杆有限元分析
2.1 厚圆盘尺寸确定
设定厚圆盘厚度e=16mm,f=30kHz,(1))式得在该频率下产生二阶弯曲振动的半径R=42mm。对所求的厚圆盘进行有限元仿真,可得其谐振频率为27.876 kHz,如图2(a)。减小厚圆盘半径以增大频率,使其与所设计频率趋于一致,修正后可得薄圆盘半径R=40mm,谐振频率为29.77kHz,结果如图2(b)所示。

图2 厚圆盘谐振频率位移分布图
2.2 杯形工具尺寸确定
设定壁高h=24mm,根据式(2 和式(3),可求得圆筒的耦合振动频率为 26.812kHz,与设计频率相差较大。调整圆盘半径使其与设计频率一致,经有限元分析可知当R=38.5mm 时大尺寸圆筒与厚圆盘耦合的杯形头其谐振频率为29.463 kHz,如图3 所示。
2.3 圆锥复合变幅杆的尺寸确定
由于所设计系统工作频率为30kHz,取D1=54mm;为提高杯形工具头的振动效果,需增大变幅杆输出与杯形工具头的接触面积取D2=27mm。设定l1=30mm,l3=30mm,将以上参数带入式(4)用MATLAB 计算可得l2=40mm。有限元仿真可得变幅杆纵向谐振频率为29.724kHz,如图4 所示。变幅杆的仿真频率与理论计算基本一致,不再进一步修正。
2.4 新型杯形工具复合变幅杆的尺寸确定
对杯形头与三段复合变幅杆组成的复合变幅杆进行有限元分析,其中材料均用45#钢,模态分析结果如图5。

图5 杯形工具复合变幅杆系统谐振位移分布图
由图5 可知,杯形头与三段变幅杆组成的复合变幅杆谐振频率为30.346kHz,与设计频率30kHz 相差346Hz,需进一步修正。调整杯形头的底厚使其频率于设计频率一致,修正后杯形工具复合变幅杆谐振频率为30.044kHz,满足设计要求。通过有限元软件的后处理功能进行路径定义、映射,提取相对位移,结果如图6 和图7 所示,可得纵向振动是径向振动约3 倍表明杯型头以纵向振动为主的纵径耦合振动形式。通过以上分析新型杯形工具复合变幅杆各部分尺寸的最终参数,如表1 所示。

表1 新型杯形工具复合变幅杆各部分具体尺寸参数
2.5 谐响应分析
为了进一步研究新型杯形工具复合变幅杆的动力学特性,在模态分析的基础上进行谐响应分析,求解计算得到新型杯型工具的位移-频率响应曲线如图8 所示,由图8 可知杯型工具右端面的位移振幅为 8.711um,则新型复合变幅杆的振幅放大系数Mp≈1.45,这表明经过杯形头振幅进一步放大。
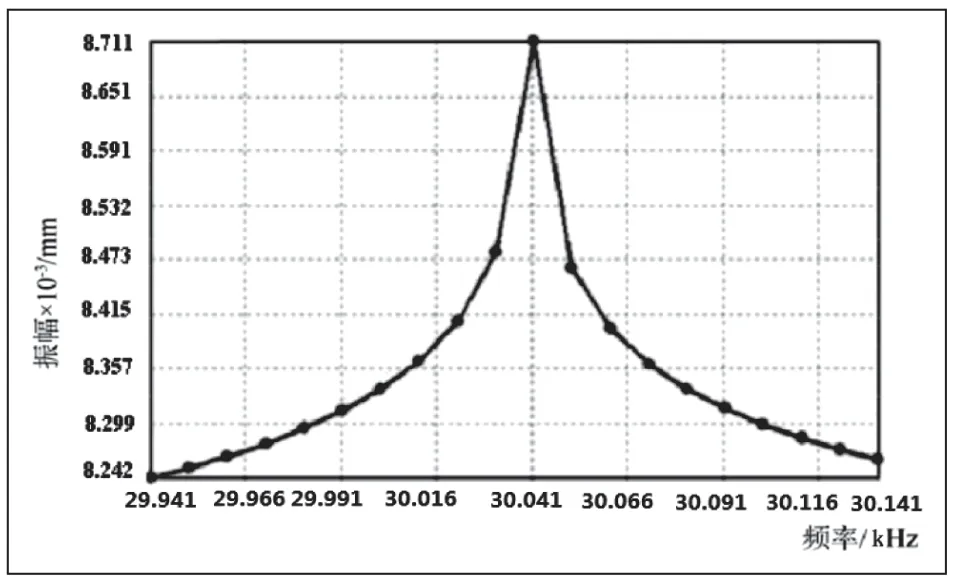
图8 新型杯形工具复合变幅杆位移—频率响应曲线图
3 新型杯形复合超声变幅杆频率特性研究
用有限元仿真从变幅杆各段长度以及杯形头壁高、底厚、内径来研究各几何形状参数对杯形工具复合变幅杆谐振频率的影响规律。
3.1 杯形头壁高 h、杯厚e 及内径 a 对杯形工具复合变幅杆谐振频率的影响
由表2 可知,在杯底厚、内径不变的情况下,随着杯壁高由 24 mm 增大到30 mm的增加,杯形工具复合变幅杆谐振频率的仿真值逐渐降低,但误差较小均在5%以内。其他条件不变时,谐振频率随着内径的增大而降低;谐振频率随着底厚的增加而增加。
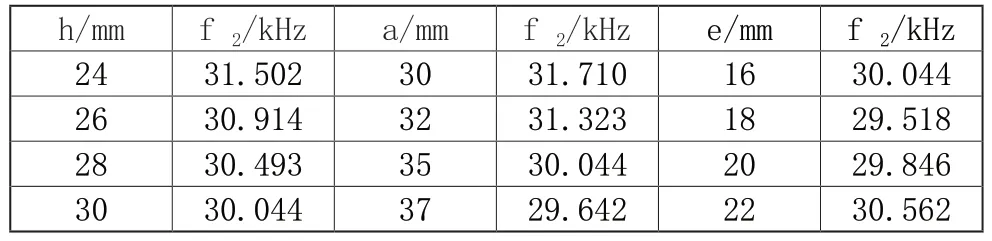
表2 新型杯形工具复合变幅杆谐振频率随杯高、杯厚和内径变化
3.2 三段复合变幅杆各段长度对振动系统频率的影响
由表3 可知,在底厚、壁高以及半径不变的条件下,杯形工具复合变幅杆的谐振频率随着变幅杆各段的增大而降低,对比可看出变幅杆各段长度对系统谐振频率的影响为:l3>l2>l1.

表3 新型杯形工具复合变幅杆谐振频率随变幅杆各段长度变化
4 实验
为了验证以上结论,按所设计的尺寸加工新型杯形工具复合变幅杆并进行阻抗特性分析。由图9 可知,实测谐振频率在29.828kHz 附近与ANSYS 模态分析结果基本吻合,且导纳圆圆度较好,电导曲线正常,表明以上所设计的变幅杆结构合理、振动效果良好。
5 结论
(1)基于Mindlin 厚板弯曲振动理论、耦合振动理论和变幅杆纵振设计理论,结合有限元分析法,设计了工作频率为30 kHz的新型超声杯形工具复合变幅杆。(2)利用有限元软件仿真分析了新型超声杯形工具复合变幅杆各几何参数对振动系统谐振频率的影响,结果表明当杯形头的壁高、内径减小时,变幅杆的仿真频率随之增加;当减小其底厚时,变幅杆仿真频率随之降低;随着变幅杆各段的增大而降低且各段影响程度不同l3>l2>l1.,其结果可作为新型变幅杆频率调节的理论参考和依据。(3)有限元仿真结果可知杯形头表现为以纵向振动为主的纵径耦合振动形式。对所设计的新型超声杯形工具复合变幅杆进行阻抗分析试验,结果表明振动系统谐振频率与仿真结果误差较小,说明所设计的变幅杆结构合理,可应用统一超声辅助加工技术特别是硬脆材料曲面高精度加工。

