农村配电网光伏与负荷相关性概率潮流计算

盛 旭

（东北石油大学电气信息工程学院，黑龙江大庆163318）

0 引言

国家提出“光伏扶贫”项目，改善贫困地区人民生活，为群众带来额外的经济收益，并积极改善配电网供给侧的改革。对于农村配电网光伏并网运行系统不确定的因素场景分析，经常利用概率潮流计算方法来解决。

国内外学者在概率潮流计算方法方面进行了大量研究[1-19]。苏宏升等[3]采用Beta分布建立光伏发电的功率概率模型，将随机行走原理应用在拉丁超立方抽样（Latin Hypercube Sampling，LHS）的排序当中去，提升LHS的计算精度，降低操作的复杂程度；颜伟等[4]针对当下光伏概率模型的拟合度不高，且不能有较好的适应性，提出核密度估计理论建立光伏概率模型，并采用拟合优度检验；任洲洋等[5]结合Beta分布模型和核密度估计模型综合建模，并且考虑分布式光伏发电和负荷相关性的影响，基于等概率转换原则结合LHS处理相关性分析，降低了计算的复杂程度。刘庭响[6]将切片采样算法与拉丁超立方算法结合，形成了CSMCMCS-L（Correlation Slice Samping MCMC simulation with Latin Hypercube Sampling）算法，降低了每个采样值之间的相关性，提升了蒙特卡洛方法的计算效率的精度。但上述文献未将光伏与负荷相关性降到最低，并且利用Cholesky分解时未考虑相关系数矩阵存在非正定的情况；而针对相关系数矩阵非正定的情况，赵亦岚等[7]借鉴遗传算法的思想，提出一种NDC-ILHS方法概率潮流计算方法，利用父代矩阵进行不断地迭代，求解子最佳矩阵，此方法计算复杂，耗时较长。

综上所述，本文针对处理相关系数矩阵非正定性的不足，提出Nataf变换结合CSMCMCS-L算法分析光伏与负荷的相关性，并且利用特征值分解法求解非正定的相关系数矩阵。该方法能处理相关系数为非正定的情况，而且有着更高的计算精度。利用IEEE33节点系统进行仿真计算，并将计算结果与NDC-ILHS方法的结果进行对比分析。

1 光伏发电功率综合概率建模

针对正态分布建立光伏发电功率概率模型不具备良好的适应性和Beta分布建立概率模型不能取得较好的模拟效果，提出光伏出力的综合建模的方法，其流程如图1所示。

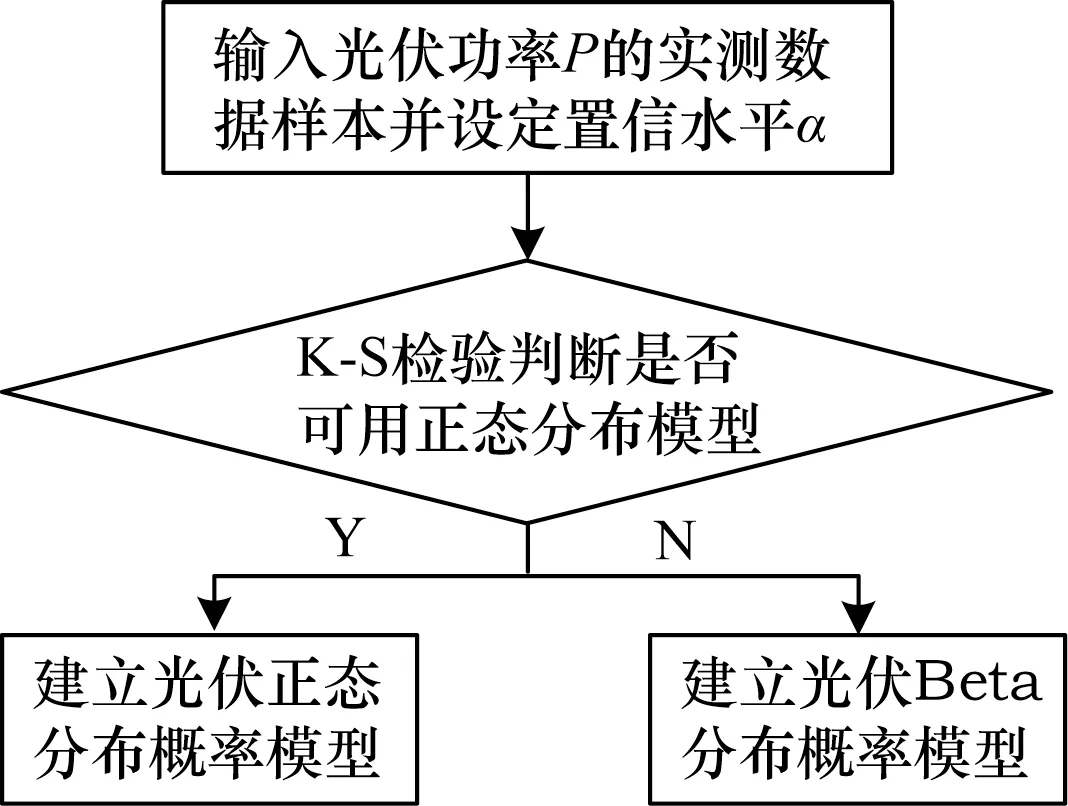
图1 光伏综合概率建模方法流程

（1）基于K-S检验方法判断是否可用正态分布模型[8]，对输入的光伏实测样本，随机取n个功率样本，对其进行从小到大排列：P1≤P2≤…≤Pn。基于K-S检验方法，判断是否可用正态分布描述P的概率分布。若可以，则建立正态分布模型；否则，采用Beta分布模型。

（2）基于正态分布的光伏概率模型，根据正态分布可估计光伏功率P的概率密度函数为：

式中：μ、σ均为光伏功率的均值和方差。

（3）基于Beta分布的光伏概率模型为：

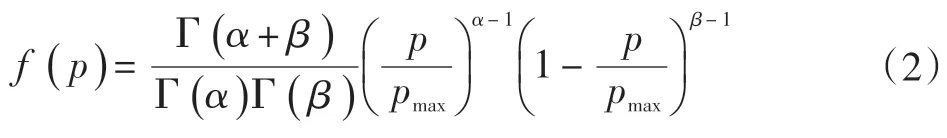
显然，该方法对于不同的光伏功率曲线分别采用不同分布描述，既能准确地描述不同随机特性的光伏功率曲线，还反映随机波动不确定性，具有较强的适应能力。

2 基于特征值分解法结合CSMCMCS-L算法概率潮流计算

在农村配电网中光伏电源输出功率与负荷相关性存在相关关系，考虑到农村配电网复杂多变性，相关系数矩阵容易出现非正定的情况。为此，首先对于随机变量运用切片采样法进行采样，得到初始样本空间，再进行拉丁超立方算法的采样与排列得到最终样本；其次，采用特征值分解法处理非正定的相关系数矩阵，使得相关性降到最低。

2.1 切片采样算法

切片采样算法[9]在采样过程中引入一个变量y，通过变量y来确定每次的采样值，从而最终形成样本空间。根据张晓英等[10]提出的方法，其生成采样值的方法通过如下步骤实现。

（1）切片生成。即给定初始值x0，确定辅助变量y值，其中y∈(0,f(x))。以y值来确定切片S的生成，并且切片随着y值不断迭代而更新。

②区间确定。以x0为中心确定采样区间I=(L,R)，需该区间尽可能将切片S囊括进去。同时，为了防止效率低，应将I的范围控制在切片S之内。Neal R M等[11]提出了Stepping-out算法来解决这一问题。首先以x0为中心确定单位宽度ω，然后以ω为单位不断迭代扩展该区间，直到某端超出切片S。

③样本采样。当区间I确定之后，则需要用Shrink⁃age算法[12]来求解下一个采样点x1。首先，令x1=-L+U再对x1进行判定。若yx0，则区间I的右边界更新为R=x1；用x1作为下次迭代的初值进行计算，最终获得样本空间。

切片采样算法示意图如图2所示。

图2 切片采样算法

2.2 拉丁超立方采样

拉丁超立方采样[13]一般分为采样和排序两步。

（1）采样：有n个随机变量x1,x2,…,xn，采样规模为N，则其累积概率分布函数为：

将纵轴分成N个大小相同的区间，在每个区间1/3处取一点为Yk的采样值；再利用（2-1）求得xk的采样值，将求得的采样值排列成n N阶矩阵S。

（2）排序：往往采取Gram-Schmidt序列正交化[14]来进行样本矩阵的排列，从而降低相关性。

2.3 Nataf变换和相关性处理

LHS往往使用在单一的随机变量采样中，当有着多个随机变量时，需要先对多个随机变量相关性进行分析。在农村配电网中，分布式电源的出力起伏不定，很难进行精确地描述，求取它们的联合密度函数较为复杂。而Nataf变换通过已知的分布模型和相关系数矩阵，可进行正态随机变量与各分布随机变量之间的转换[15-17]。

有n个随机变量x1,x2,…,xn，其随机变量之间的相关系数为ρij，则：

式中：σi和σj分别为随机变量Xi、Xj的标准差。

由等概率转换原则得：

其中y为标准正态随机向量，而标准正态累积分布函数Φ(*)的相关系数为由Nataf变换可知：

式中：F(ρij)为变系数，且F(ρij)≥1，取决于Xi、Xj的分布。

对相关系数矩阵进行特征值分解：

根据定理可知[18-20]，若RY为m阶对称矩阵，则存在矩阵U，使得UΛU-1=UΛUT，其中Λ是对角矩阵。

假设存在矩阵B，可以将具有相关性的变量Y转换为不相关的变量Yx：

假设Cx为单位矩阵，则：，从而：

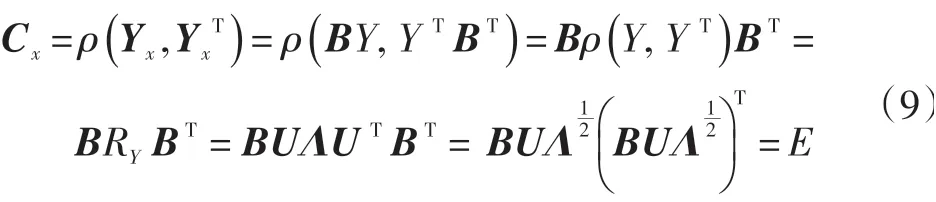
基于LHS，在其中排序过程中进行改进，具体步骤如下。

（1）设光伏功率的概率累积分布F(p)，其相关系数矩阵RY=[ρij]T，通过上述Nataf变换对相关系数矩阵 变 换，再对RY进行特征值分解得到矩阵B=(UΛ12)-1。

（2）对独立标准正态分布Y进行采样，得到矩阵Wn N，令矩阵Z=BW，则矩阵Z的相关关系为RY，从而得到Z顺序矩阵LS。

（3）对随机变量X进行样本采样，并按照矩阵LS的顺序进行排列，得到最终的样本矩阵S。

（4）由样本矩阵S及输入与输出随机变量之间的关系，采用Monte Carlo模型技术求解节点电压，线路传输功率等样本信息。

3 算例分析

基于Inter Core i5-4200 M 2.5 Hz 4GB搭建IEEE33节点系统仿真平台，设置了蒙特卡洛模拟法（MCS），NDC-ILHS算法以及基于特征值分解法结合CSMCMCS-L算法来计算PLF。

假设系统共接入4个光伏电源P1、P2、P3和P4，其中P1和P2额定容量分别为200 kW和400 kW，服从形状参数为0.45和9.18的Beta分布；P3和P4额定容量分别为200 kW和400 kW，输出功率样本为某农村地区光伏电站实测样本数据，经K-S检验可知，光伏功率服从正态分布，故建立P3和P4的正态分布概率模型。将P1、P2、P3和P4依次接在节点17、18、32和33处。33节点配电系统如图3所示。

图3 33节点配电系统

综合考虑仿真时计算精度和时间，采用MCS法设置10 000次随机采样，将MCS法计算出来的结果作为标准与本文方法和NDC-ILHS方法作对比，比较得到的节点电压，支路潮流的概率分布，以此评价两者方法的准确性与有效性。

其中，光伏与负荷相关系数矩阵均为非正定矩阵。

以MCS法所得结果作为仿真结果准确程度的判断依据，采用10 000次抽样的MCS计算结果作为参考值。同时对比运用500次抽样的本文方法与NDC-ILHS方法计算得到配电网的参数信息，以此评价两者方法的准确性与有效性。

在考虑负荷和光伏相关性的情况下，以10 000次抽样的MCS为标准，图4所示为计算本文方法与NDC-IL⁃HS方法所得到节点17的电压幅值概率分布；图5所示为计算本文方法与NDC-ILHS方法所得到支路32的有功和无功的概率分布。由图可知同样抽样条件下，本文方法得到的电压概率分布比较接近标准的MCS计算结果。

图4 3种方法计算节点17的电压幅值概率分布

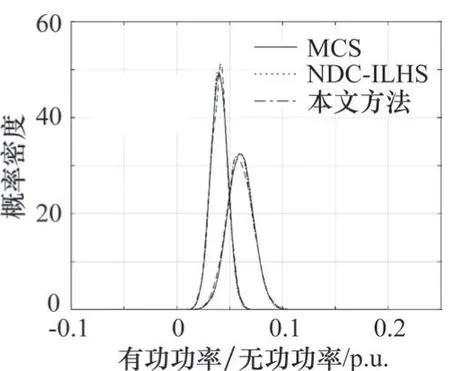
图5 3种方法计算支路32的功率概率分布

为了验证本文方法相较于NDC-ILHS法的准确性，采用相对误差和的根均值指标（Average root mean square，ARMS）作为参考指标，将误差量化。主要用来度量所提方法输出变量在统计方面的准确性。

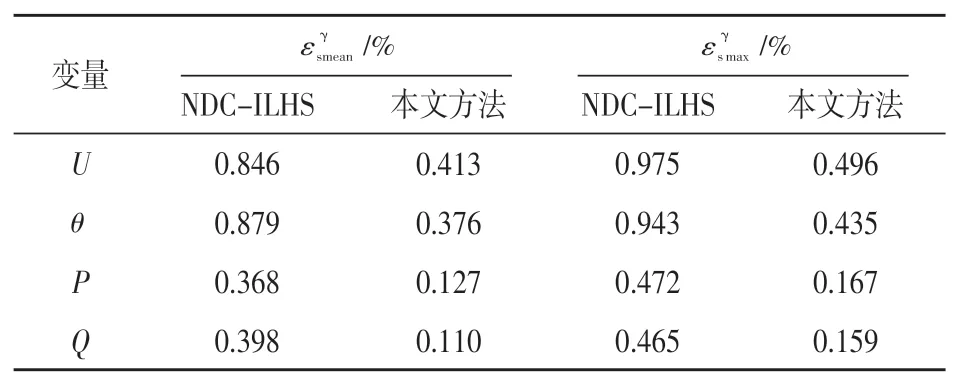
表1 输出变量的相对误差指标

表2 输出变量的ARMS指标

算例10 000次抽样MCS计算时间为135.23 s，NDC-ILHS方法计算时间为30.45 s，本文方法计算时间为10.3 s，说明了本文方法在采用蒙特卡洛抽样法下具有计算速度较快的优点。

分析光伏和负荷的相关性对系统节点电压产生的影响，以节点17为例，设定其相关系数分别为0.1、0.5和0.9，并采用本文方法依次计算概率潮流。

不同相关系数情况下，光伏与负荷的相关性对配电网上的电压影响不大，如图6所示；如图7所示，随着相关性的增加对电压的标准差影响随之增大；如图8所示，不同相关系数情况下，节点电压的概率密度函数也不相同，但并未发现其规律性。

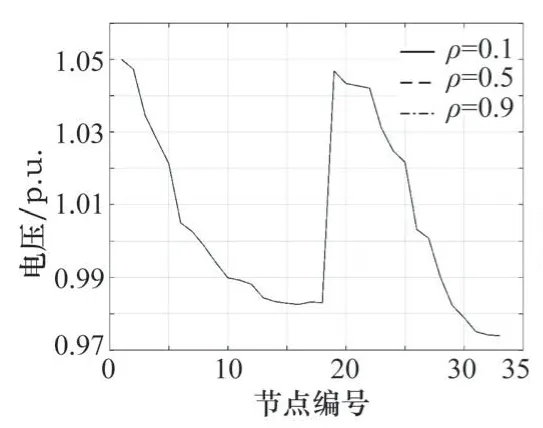
图6 节点电压均值

图7 节点电压标准差

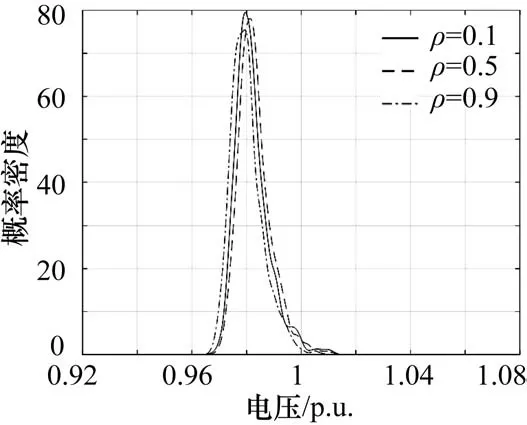
图8 节点17电压的概率密度曲线

4 结束语

在农村配电网中，针对目前概率潮流计算方法处理随机变量相关系数矩阵非正定的不足，提出一种将光伏综合建模方法与改进的CSMCMCS-L方法相结合应用于概率潮流中求解得到以下结论。

（1）建立光伏出力综合建模的方法，相较于传统的Beta分布建模，可以准确地模拟出不同分布特性的光伏功率，还具有较强的适应性。

（2）用特征值分解代替Cholesky分解，可解决相关系数矩阵非正定的情况，相较于NDC-ILHS方法，本文方法所需时间少，计算简单，所得结果精度更高。

（3）随着相关系数的不断改变，对配电网电压的幅值影响较小，而电压的标准差随之增大。