晴朗天气下全天空域偏振定向方法*
蔡 弘,张 然,关 乐,万振华,褚金奎※
(1.大连理工大学机械工程学院,辽宁大连116023;2.大连大学机械工程学院,辽宁大连116622)
0 引言
非偏振的太阳光传输到大气中,会被大气中的尘埃、分子以及气溶胶等微粒散射和吸收,从而变成部分偏振光[1]。晴朗天空的偏振模式符合瑞利单次散射理论,在某一时刻某一位置对应的天空偏振模式是稳定的,太阳的位置随着时间及观测地点的变化而有规律的移动,因此在天空偏振模式下获取载体坐标系下太阳方位角可以用于导航定向[2-3]。
当前天空偏振导航系统主要分为点源式和图像式。本课题组较早使用点源式偏振导航系统,并基于瑞利散射理论获取载体坐标系下太阳方位角[4-7]。但由于点源式偏振导航系统局限于测量天空某几个点的偏振信息,不能很好地测量全天空域的偏振信息,易受环境噪声的影响。于是开发了图像式偏振导航系统[8-9]。国防科技大学使用分通道式的图像偏振导航系统在晴朗天气下最大定向误差为0.5°[10],由于多个通道不是经过同一镜头入射到CMOS焦平面上,存在瞬时视场误差。
当前在晴朗天气下利用天空偏振场图获取太阳方向的算法主要为识别太阳子午线,因为在晴朗天气下偏振方位角关于太阳子午线具有很好的对称性。清华大学提出基于霍夫线变换提取太阳子午线的方法,在晴朗无云天气下精度为0.313°[11]。中北大学使用分通道式的图像偏振导航系统基于最小二乘法拟合太阳子午线[12],本课题组提出分箱法拟合太阳子午线[13]。
由于太阳子午线上偏振光信息并没有天空图像中全局偏振光信息丰富,利用拟合太阳子午线方法比基于瑞利散射理论获取太阳方向方法所使用的天空偏振光束少,拟合太阳子午线方法在完全被遮挡情况下可能会失效,同时研究表明,生物中昆虫的复眼也是利用多个方向的偏振小眼感知大视场天空区域的偏振光[14-15]。本文为了获取更大视场的天空偏振光,使用鱼眼镜头结合偏振相机搭建图像式偏振定向测量系统,提出一种以信标发光二极管为基准的鱼眼镜头天顶角标定方法,利用瑞利散射理论和太阳矢量约束计算载体坐标系下的太阳方位角。室外实验表明本文方法比拟合太阳子午线的两种方法(最小二乘法、分箱法)误差更小。
1 理论
1.1 获取天空偏振场图
图1 所示为实验所用设备,实验时主要使用三脚架支撑偏振探测系统,通过网口连接电脑采集天空图像。偏振探测系统包含鱼眼镜头和偏振相机,偏振相机主要由微透镜阵列、偏振片阵列以及像素阵列组成,其中偏振片阵列包含0°、45°、90°和135°共4个偏振方向。

图1 实验设备
斯托克斯矢量表达式如下:

I、Q、U三个变量的获取如下:

偏振度DOP表征天空偏振态,计算如下:

偏振角AOP是载体坐标系中天空观测点的偏振方向矢量与载体(相机)体轴的夹角,计算如下:

偏振方位角AOE是天空观测坐标系中天空观测点的偏振方向矢量与当地子午线切线方向的夹角,计算如下:

式中:(i,j)为像素点坐标;h为图像的高;w为图像的宽。
1.2 获取载体坐标系下太阳方位角
图2 所示为晴朗天空偏振分布模式,以地面观测点为原点建立载体坐标系(即相机坐标系XcYcZc),在载体坐标系中太阳方向矢量OS与轴Zc的夹角γs为太阳天顶角,OS与轴Xc的夹角a′s为载体坐标系下太阳方位角。天空观测方向矢量OP与轴Zc的夹角γ为天空观测点天顶角,OP与轴Xc的夹角a为天空观测点方位角,天顶角的角度范围为闭区间[0°,90°],方位角以轴Xc正方向为0°,逆时针方向为正,顺时针方向为负,角度范围为闭区间[-180°,+180°]。

图2 晴朗天空偏振分布模型
图中的偏振方向矢量E在载体坐标系中表示为cE,在天空观测点坐标系中表示为iE。在相机坐标系中天空观测点P位置的偏振方向矢量cE表示为:

以天空观测点P为原点建立天空观测坐标系XiYiZi,P位置的偏振方向矢量iE与轴Xi正方向的夹角φ为偏振方位角即AOE,该矢量表示如下:

cRi表示天空观测坐标系相对载体坐标系的旋转矩阵,包含了天空观测点方位角a和天空观测点天顶角γ的具体展开形式为:

由于鱼眼镜头采集的图像存在较大的径向畸变,径向畸变主要影响天空观测点的天顶角,因此为了获取准确的天空观测点的天顶角,对像素距离(图像中像素点与图像中心的距离)与天空观测点的天顶角进行标定。图3所示为鱼眼镜头的天顶角标定原理,固定偏振相机与鱼眼镜头,将发光二极管与鱼眼镜头的光轴对齐,并绕镜头的光心逆时针旋转,每旋转一次对应的观测点的天顶角γ累加10°并采集图像,共旋转9次,旋转角度范围为闭区间[0°,90°],模拟了半球状的天空分布。每一位置的发光二极管在图像中对应一个像素点,例如位置A处的发光二极管在图像中对应着像素点A′,同理B对应着B′。要标定观测点的天顶角γ与像素距离(图像中像素点与图像中心A′的距离)的映射关系。将实际得到的观测点的天顶角γ作为因变量,对应的像素距离作为自变量,可以得到9个点:(36.0,10),(73.0,20),(110.0,30),(146.0,40),(182.0,50),(219.0,60),(255.0,70),(291.1,80),(327.1,90)。用Matlab曲线拟合工具箱拟合观测点的天顶角γ与像素距离(dis)之间的映射关系,当γ=0.2688dis∧1.004时,均方根误差最小,为0.105。

图3 鱼眼镜头天顶角标定原理
根据瑞利单次散射理论,任意天空观测点P的偏振方向矢量cE垂直于由天空观测点P、太阳S及地面观测点O组成的平面,则cE垂直于OS。天空中所有符合瑞利散射的点在相机坐标系中的偏振方向矢量组成矩阵理想情况下:

但实际由于误差存在,需对太阳方向矢量作最优估计:

式(13)为对式(12)中函数f(OS)求导,为了获取该函数的最小值,令导数等于0。由于OS不为零向量,则则f(OS)min=λmin,则太阳方向矢量OS的最优估计为矩阵的最小特征值λmin对应的特征向量。
2 实验与结果
实验时间为2020年12月19日,天空晴朗无云,实验地点为大连理工大学机械学院2号楼楼顶,坐标为(121.538 857,38.886 469)。实验时用图1所示设备采集11:25—14:16这一时间段的天空强度图。大概是每隔10 min采集一次,如表1所示,共采集了14组数据。实验过程以11:25时采集的天空图像获取载体坐标系下太阳方位角为例,如图3所示。

表1 实验数据(°)
图4 包含4张图像,均裁剪为400×400大小并做伪彩色处理。第一张为天空强度(Image)图,为斯托克斯矢量中的I变量,第二张为偏振度(DOP)图,第三张为偏振角(AOP)图,第四张为偏振方位角(AOE)图,AOE图中Xc轴为载体体轴,图中标记的黑线表示太阳子午线的位置,夹角a′s为载体坐标系下太阳方位角。图4中Image图显示了存在太阳过曝区域,该区域对应的DOP=0,实验时将DOP=0的像素点过滤,然后用本文提出的算法获取载体坐标下太阳方位角。

图4 获取太阳方向实验过程
表1 所示为14组实验数据,每一组标注了地理坐标系下太阳方位角和太阳天顶角,通过查阅天文年历可以获得。并列出了最小二乘法拟合太阳子午线[12]、分箱法拟合太阳子午线[13]以及本文算法这3种方法获取的载体坐标系下太阳方位角。
图5 所示为14组数据的太阳相对转角的曲线,其中▇曲线表示理想太阳相对转角,通过将每组的地理坐标系下太阳方位角与第一组作差得到,●曲线表示用最小二乘法得到的太阳相对转角组成的曲线,▲曲线表示用分箱法得到的太阳相对转角组成的曲线,▼曲线表示用本文算法得到的太阳相对转角组成的曲线,这3种方法获得的太阳相对转角均是将每组的载体坐标系下太阳方位角与第一组作差得到。可以看出图中的4条曲线具有相同的变化趋势,但其中●曲线与▇曲线(理想太阳相对转角)每组数据有较大偏差,而▼曲线相比于▲曲线,其与▇曲线每组数据更较为接近,说明本文算法获取的太阳相对转角更加准确。

图5 太阳相对转角
为了更好地说明本文算法的优越性,对上述3种算法分别与理想太阳相对转角作差并拟合了3条曲线,如图6所示。由误差曲线图可以看出▼曲线波动最小且一直在0附近变化。又分别计算3种算法的均方根误差(RMSE),最小二乘法为3.12°,分箱法为0.9°,本文算法为0.28°。本文算法的均方根误差最小,因此,本文算法要优于另两种算法,在晴朗无云的天气下具有可行性。
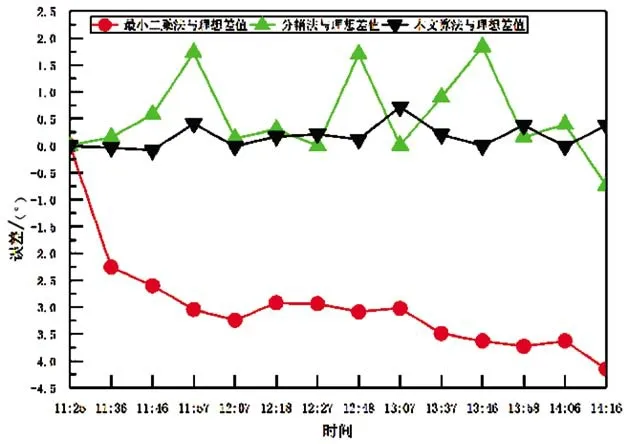
图6 误差曲线
3 结束语
本文首先基于斯托克斯矢量获取天空偏振场图,然后提出一种以信标发光二极管为基准的鱼眼镜头天顶角标定方法,利用瑞利散射理论和太阳矢量约束计算载体坐标系下的太阳方位角,最后进行实验分析。通过与拟合太阳子午线的两种算法(最小二乘法和分箱法)比较,本文算法具有最小的均方根误差,在实际的晴朗无云天气下进行导航定向具有可行性。

