无刷直流电机模糊PID控制及建模仿真*
郭文韬,单树清,刘二林,马殷元,金宝宝,钟佩甫,张 正
(兰州交通大学创新创业学院,兰州730070)
0 引言
随着永磁材料和电子技术的不断发展,无刷直流电机(Brushless DC Motor,BLDCM)进入了快速发展阶段。与有刷直流电机相比,无刷直流电机利用功率管电路的电子换相代替有刷直流电机的机械换相,消除了有刷直流电机发生故障的主要根源[1]。无刷直流电机结构紧凑、效率高、可靠性强,并且兼有有刷直流电机的良好机械特性和调节特性,广泛应用于工业精确控制、精密伺服系统、医疗设备等领域[2]。无刷直流电机有着广阔的应用前景,对其精准控制等方面深入研究有很大的必要性。
目前,BLDCM控制系统国内外研究热点主要有3个方向:(1)转矩脉冲转动抑制;(2)位置检测技术;(3)智能控制算法对于无刷直流电机的控制优化[3]。谢志诚等[4]在MATLAB软件中建立无刷直流电机控制系统仿真模型,编写单神经元PID速度调节器的S-Function函数,实现电机仿真,取得良好的控制效果。马晓爽等[5]采用速度PI控制和电流PI控制双闭环控制系统,在MATLAB/Simulink平台搭建仿真模型,在不同负载下,控制系统表现出有着良好的动态和静态性能。本文分析了无刷直流电机的数学模型和工作原理,在MATLAB/Simulink环境中搭建出无刷直流电机控制系统仿真模型,采用双闭环模糊PID控制算法对控制系统进行速度调节,得到电机的转速和转矩等参数波形图,并与传统PID控制算法相比较,仿真结果验证了双闭环模糊PID控制算法对电机控制具有良好的控制效果。
1 无刷直流电机原理
无刷直流电机由电机本体、位置传感器、控制系统三部分组成。其基本原理是根据位置传感器从电机转子检测转子位置信息,控制驱动电路根据转子位置信号,输出PWM波驱动逆变桥依次按顺序导通,产生旋转磁场驱动永磁转子转动[6],控制原理如图1所示。
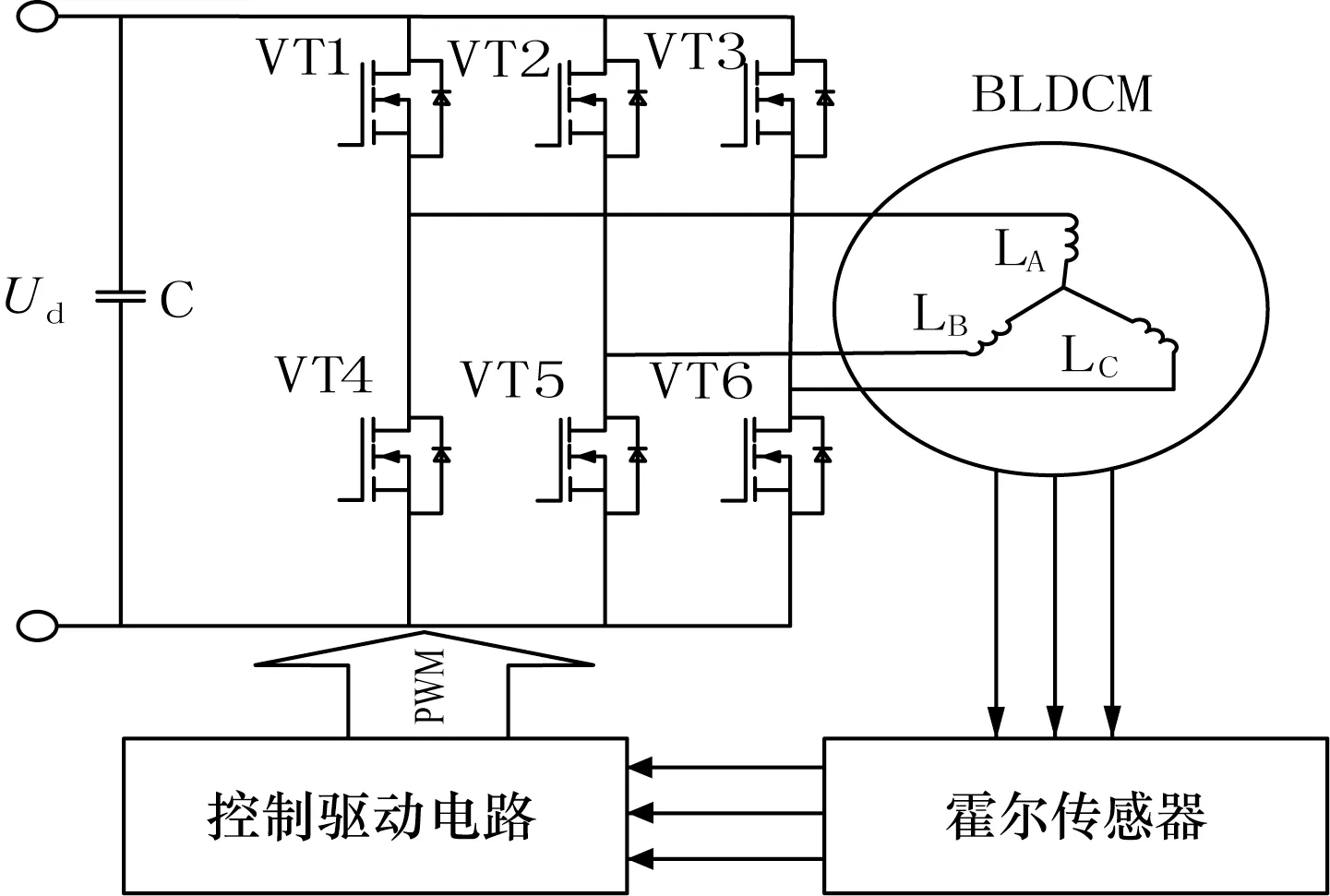
图1 无刷直流电机控制原理
电机本体结构类似于倒装式的直流电机,恰与有刷直流电机安装结构相反,转子侧安装永磁体,定子侧安装有三相电枢绕组,分为A、B、C三相,每相间隔120°电位差,采用星型连接。
位置传感器采用霍尔传感器,利用霍尔效应检测转子磁极的相对位置,计算为驱动控制电路提供转子位置信息,并计算转子实际转速。驱动控制电路根据转子位置信号通过驱动三相全桥逆变桥按顺序导通,实现电机的电子换相功能。换相采用两两导通方式,每次有两个功率开关导通,每隔60°逆变桥便会改变一次导通状态,每个开关连续导通120°[7]。
2 无刷直流电机数学模型
控制系统中的全桥逆变驱动方式为两两导通星型连接,采用电机的相变量建立无刷直流电机的数学模型和时域状态方程,计算结果也较为准确。为了分析过程便于分析,需要在电机理想状态下运行,本文对电机做出以下几点假设[8]:(1)电机三相绕组完全对称且各绕组电阻、电感、互感等各参数均一致;(2)驱动电路中功率开关的通断反应条件均处于理想状态;(3)齿槽效应忽略不计;(4)定子绕组的反电动势假定为平顶宽度为120°的梯形波;(5)磁芯饱和、涡流损耗和磁滞损耗等忽略不计。
2.1 电压方程
基于上述假设以及无刷直流电机特性,根据无刷直流电机的等效电路(图2),可得到无刷直流电机电压方程:
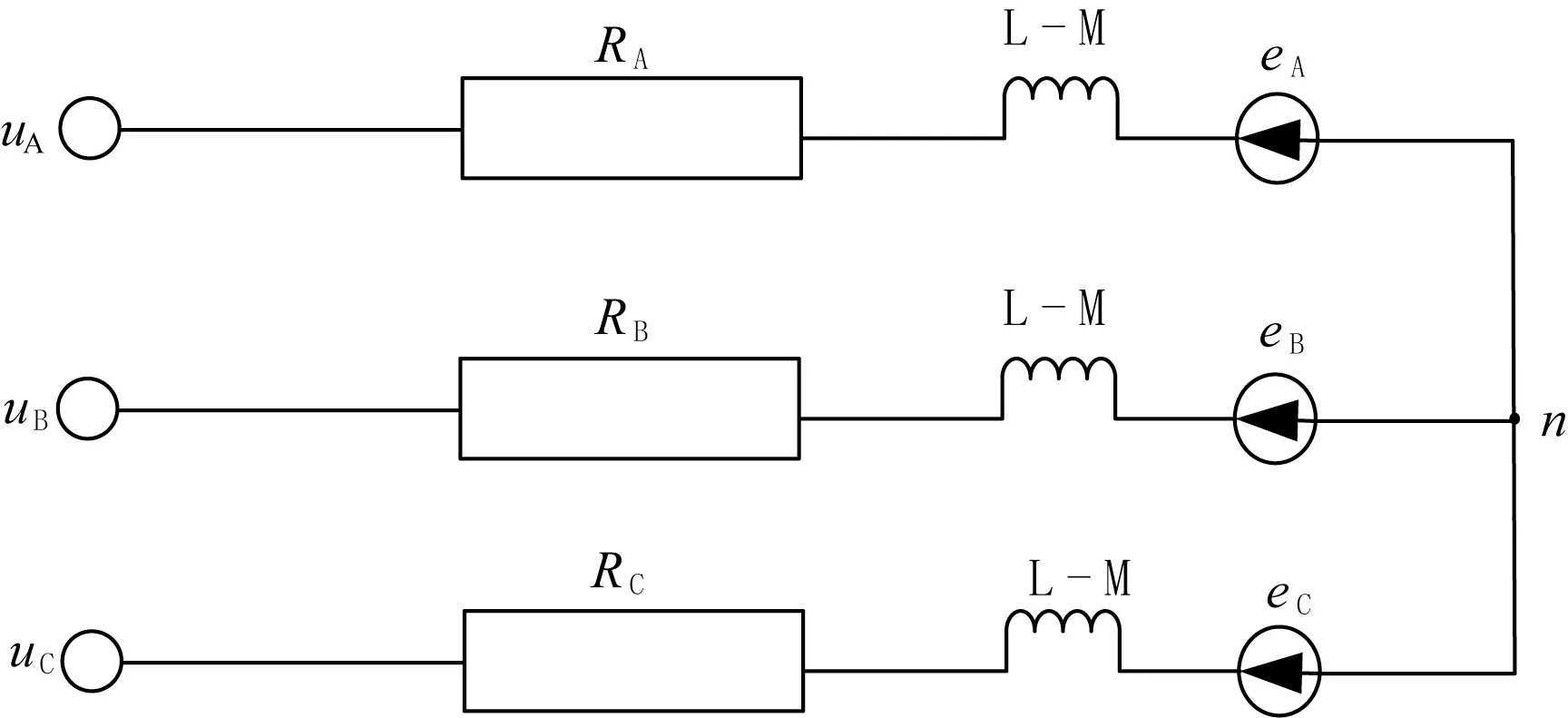
图2 无刷直流电机等效电路

式中:uA、uB、uC分别对应的是电机定子三相绕组端电压,V;iA、iB、iC分别对应的是电机三相绕组相电流,A;RA、RB、RC分别为三相绕组的相电阻,Ω;LA、LB、LC为三相绕组的电感,H;LAB为三相绕组中的A相绕组和B相绕组之前的互感,H;即LAC、LBA、LBC、LCA、LCB均为两相绕组之间的互感,H;eA、eB、eC分别为电机三相绕组反电动势,V;un为绕组的中心点电压,V。
本文电机电枢绕组采用星型连接,相电流之间关系为:

无刷直流电机在上述假设的理想状态下,由于电枢绕组为三相完全对称结构,各绕组的互感和电阻相同,进而三相电枢绕组的两两绕组之间的互感也是相同的,因此,得出以下关系:
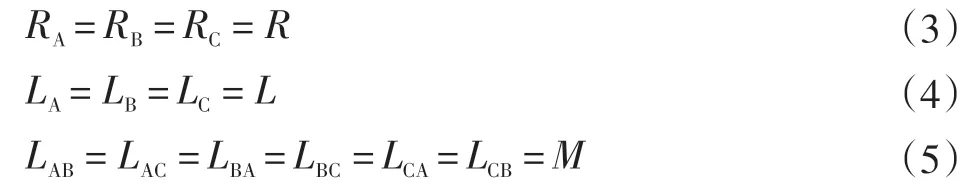
进一步化简,最后得到电机电压方程:

2.2 电磁转矩方程
电机运行时,从电源吸收的电功率主要铜耗、铁耗及电磁功率3部分组成。其中铜耗和铁耗占总功率中的极小部分,转子力矩占主要部分,这部分功率就是电磁功率。忽略铁耗和铜耗后,电磁功率是定子三相绕组的相反电动势与相电流的乘积之和:

在电机空载工况下,忽略转子的机械损耗和其他损耗,则电机的电磁功率将全部转化为转子动能:

式中:Pe为电磁功率,W;Te为电磁转矩,N∙m2;ω为电机机械角速度,rad/s。
2.3 电机运动方程
在电机工作时,根据电机转子本身特性及负载状况,可得出电机运动方程:

式中:TL为负载转矩,N∙m;J为电机转子转动惯量,N∙m;BV为粘滞摩擦因数。
式(7)、(10)、(11)共同组成了电机的数学模型公式。
3 无刷直流电机控制系统仿模型
基于无刷直流电机的主要工作原理及数学模型,利用MATLAB/Simulink工具进行电机控制系统进行仿真。无刷直流电机控制系统具有非线性、强耦合性等特征,传统PID控制算法无法精准地实现无刷直流电机转速控制,本文采用模糊PID双闭环控制算法对无刷直流电机控制系统进行分析,并在Simulink中搭建出无刷直流电机的双闭环模糊PID控制系统仿真模型。
3.1 电机总体模块
电机总体模块是无刷直流电机控制系统的控制对象,由3部分组成:电压模块、转矩模块和电机运动方程模块。主要依据无刷直流电机的数学模型和基本工作原理搭建而来,如图3所示。
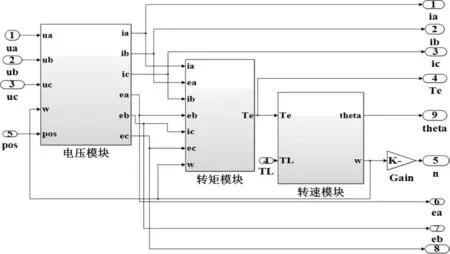
图3 电机总体模块
3.1.1 电压模块
目前求取电机反电动势主要有3种方法:傅里叶变换法、有限元法及分段线性法。与另外两种方法相比,分段线性法结构简单、精准度较高、计算量小。在MAT⁃LAB中利用S-function函数,根据转子的相对位置,将转子一个运行周期分成6个阶段,根据某时刻转子的相邻两个状态夹角位置和转速信号,确定各相反电动势的状态。
位置传感器检测的转角信号不能直接使用,需要将转子信号转换为电机的位置信号,通过Simulink中的S-Function函数计算可得。各相反电动势状态如表1所示。

表1 转子位置和反电动势关系
根据转子实时位置,电机反电动势不断变化,电压模块是根据电机三相端电压和电机反电动势输出电机的三相电流,仿真模型如图4所示。
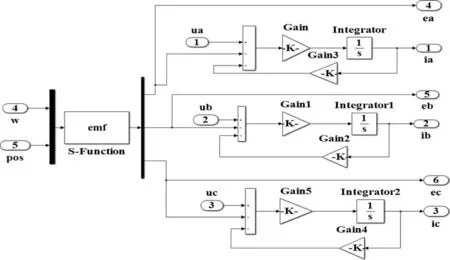
图4 电机本体仿真模型
3.1.2 转矩模块
根据无刷直流电机的转矩方程式可得出电机转矩模块。其输入为电机本体模块中的输出电流、反电动势以及角速度,输出为电机转矩,仿真模型如图5所示。
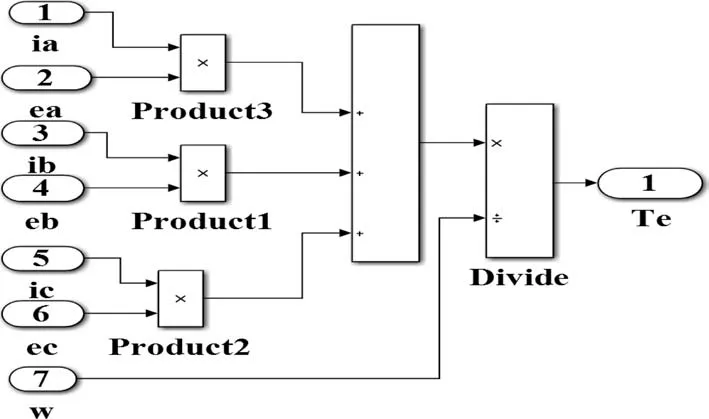
图5 转矩模块
3.1.3 转速模块
电机转速模块是根据无刷直流电机的运动学方程式而得,由输入的电磁转矩和负载转矩经过数值算法,输出得到电机角速度w。通过转速计算公式即可得到电机的转速模块[8]如图6所示。

图6 转速模块
3.2 电压逆变模块
逆变模块主要作用为将功率变换将输入的直流电压根据PWM波脉冲信号控制下转变为可调节的电压和频率。在Simulink提供通用逆变器,其中包含有MOSFET等功率开关,可设置为三相全桥MOSFET功率开关模式,简化了使用6个全桥逆变电路。逆变模块的输入直流电源和PWM波信号,通过三相全桥功率开关得到三相电压uA、uB、uC。电压逆变模块如图7所示。
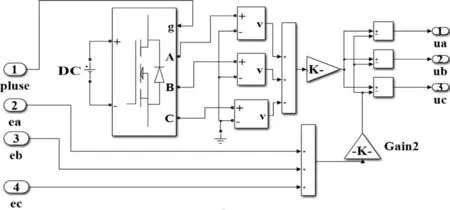
图7 电压逆变模块
3.3 转速模糊控制模块
本文转速控制模块采用模糊PID控制算法,模糊PID算法根据设定转速和实际转速之间的误差及误差变化率,记过模糊控制算法的模糊推理对PID参数值进行实时自整定,调节PID参数,达到良好的控制效果[9]。
利用MATLAB中的Fuzzy Logic Toolbox,输入为误差E和误差率EC,输出变量ΔKp、ΔKi、ΔKd,通过修正参数ΔKp、ΔKi、ΔKd,对PID控制器中的参数值进行不断修正,提高PID控制的时变性、鲁棒性和抗干扰能力。输入E、EC和输出ΔKp、ΔKi、ΔKd的基本论域均选取为[-3 3]变化范围,共分{-3,-2,-1,0,1,2,3}7个等级。各变量的基本论域相对应的模糊子集为{NB,NM,NS,Z,PS,PM,PB},即{负大,负中,负小,零,正小,正中,正大}。输入变量E和EC采用的高斯型隶属度函数,输出变量ΔKp、ΔKi、ΔKd均采用三角形隶属度函数。通过专家经验和长期试验结果,设定模糊控制规则,如表2~4所示。

表2 ΔKp模糊规则表

表3 ΔKi模糊规则表
设定控制规则后,输出值ΔKp、ΔKi、ΔKd论域范围内随输入E、EC变化的变化而不断发生变化,其变化如图8~10所示。

图8 ΔKp变化
经过模糊控制器的模糊计算,得到3个整定参数ΔKp、ΔKi、ΔKd,对PID控制器进行在线调整,最终得到的输出量为三相电流的参考电流的幅值。转速模糊控制仿真模块如图11所示。
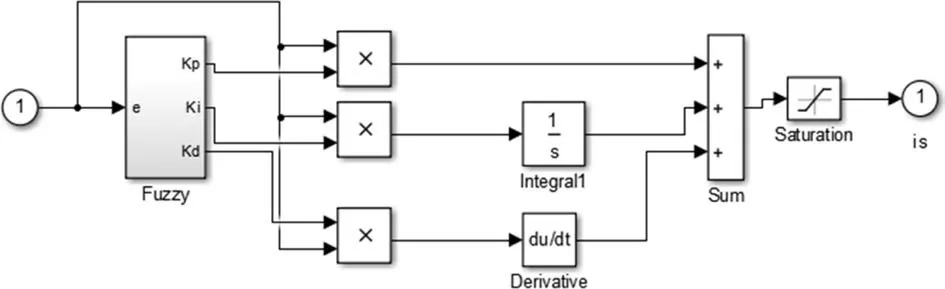
图11 转速模糊控制仿真模块

表4 ΔKd模糊规则表
3.4 参考电流模块
三相参考电流,采用分段线性法,在Simulink中利用S-Function函数,根据转子位置信号不断变化,求得三相参考电流在不同电机转子位置时的三相参考电流不同状态,如表5所示。

表5 参考电流与转子位置信号关系表
3.5 电流控制模块
滞环控制器是控制系统的电流控制模块的核心内容,其主要作用是对电机电流进行调节。滞环模块输入为三相参考电流及三相实际电流,通过参考电流与实际电流之间的电流差Δi与滞环控制器中设定的滞宽h相比较,根据Δi和h之间的大小关系,判断功率管的导通与关断。同时调节实际电流上升和下降,保证实际电流在设定允许范围之内。由控制功率开关输出PWM波信号,作为电压逆变器的输入脉冲信号。电流滞环控制模块如图12所示。

图12 电流滞环模块
3.6 控制系统仿真模型
无刷直流电机控制系统主要包含上述的电机总体模块、电流滞环模块、电压逆变模块、参考电流模块、转速控制模块等部分,按照逻辑顺序将上述子模块进行有序组合,搭建成完整的无刷直流电机控制仿真模型,如图13所示。

图13 无刷直流电机控制系统仿真模型
3.7 仿真结果
控制系统仿真模型以空载启动方式,电机绕组为R=3.4 Ω,定子电感L=0.002 H,互感M=-0.006 H,输入电压DC24 V,转动惯量J=0.000 32,参考转速n=1 000 r/min,验证电机的静态和动态调节性能。从相电压、转矩等仿真波形,可以看出电机控制系统的仿真性能,从仿真图中可以看出,电机三相电压较为平稳,电机转矩在启动后趋于稳定。如图14~15所示。
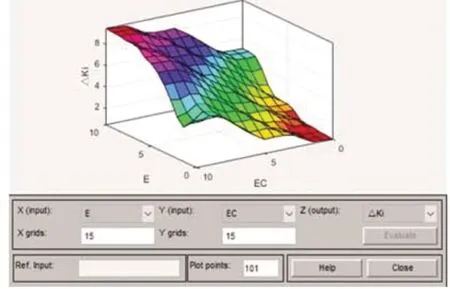
图9 ΔKi变化

图10 ΔKd变化
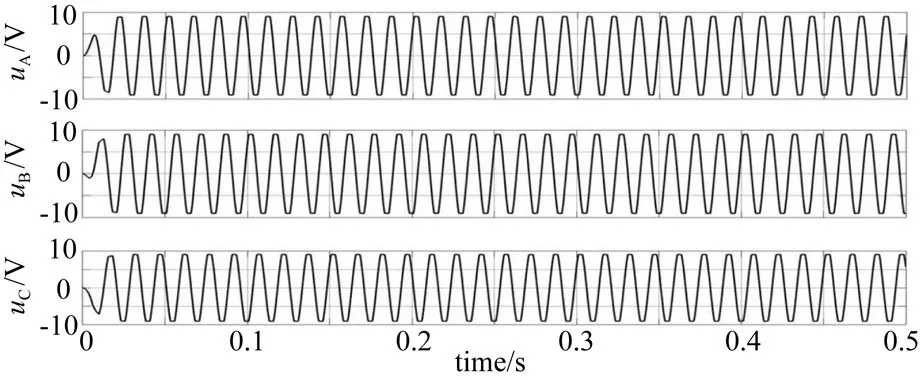
图14 电压uA、uB、uC波形

图15 转矩Te波形
在相同条件下,搭建出普通PID控制系统,与模糊PID控制仿真模型相比较,两者转速波形如图16所示。
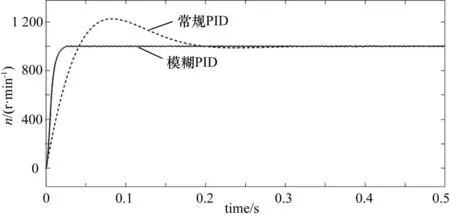
图16 两种转速n波形
从图16中可以看出模糊PID控制系统和传统PID控制系统相比,超调量小,响应速度快,电机能够快速达到设定转速值,并保持稳定,仿真结果表明,模糊PID控制具有更好的调速控制效果。
4 结束语
本文对无刷直流电机控制系统进行数学模型推导以及控制系统仿真模型搭建,通过采用速度环和电流环双闭环控制,采用模糊PID控制算法对控制系统进行仿真验证,与理论分析基本相吻合,模糊控制对PID参数进行整定,能够对无刷直流电机实现良好的动态响应和动态调节。该模型在Simulink中采用模块化和S-Function函数设计,采用模糊控制算法实现控制策略,为无刷直流电机控制的分析等方面提供参考学习。

