基于镜像对称参考切片的多扫描链测试数据压缩方法
邝继顺 刘杰镗张 亮
(湖南大学信息科学与工程学院 长沙 410082)
基于镜像对称参考切片的多扫描链测试数据压缩方法
邝继顺 刘杰镗*张 亮
(湖南大学信息科学与工程学院 长沙 410082)
为了减少测试数据和测试时间,该文提出一种基于镜像对称参考切片的多扫描链测试数据压缩方法。采用两个相互镜像对称的参考切片与扫描切片做相容性比较,提高了相容概率。若扫描切片与参考切片相容,只需要很少的几位编码就可以表示这个扫描切片,并且可以并行载入多扫描链;若不相容,参考切片被该扫描切片替换。提出一种最长相容策略,用来处理扫描切片与参考切片同时满足多种相容关系时的选取问题。根据Huffman编码原理确定不同相容情况的编码码字,可以进一步提高测试数据的压缩率。实验结果表明所提方法的平均测试数据压缩率达到了69.13%。
测试数据压缩;多扫描链;相容性;参考切片;扫描切片
1 引言
随着现代工业技术的不断发展,数字电路的集成度越来越高,单个芯片上集成的知识产权核(Intellectual Property, IP)越来越多、功能越来越复杂。测试在确保芯片的质量方面起了至关重要的作用。在测试过程中,为了保证较高的测试故障覆盖率,需要大量的测试数据,对自动测试设备(Automatic Test Equipment, ATE)的存储容量要求越来越高。测试数据压缩能有效减少需要存储的数据量,降低对ATE存储容量和带宽的要求。随着电路规模越来越大,被测电路(Circuit Under Test, CUT)的测试扫描链越来越长,单扫描链结构需要的测试时间也随之增加。多扫描链结构是将一条长的单扫描链分割成多条相对较短的扫描链,使测试数据能够并行载入扫描链,从而大大地减少测试时间。因此基于多扫描链结构的测试数据压缩是解决存储容量和测试时间的有效方法之一。
测试数据压缩分为激励压缩和响应压缩,本文主要研究测试激励压缩。测试激励压缩方法总体可以分为3类:基于线性解压结构的压缩方法、基于广播扫描的压缩方法和基于编码的压缩方法[1]。目前基于编码的压缩方法有很多,如FDR码[2]、可变长Huffman编码(VIHC)[3]、最优选择Huffman编码(OSHC)[4]、共游程码[5]和一位标识混合编码[6]。这些编码方法都有较好的数据压缩率,但是一般只针对单扫描链的CUT。然而现代的片上系统(SoC)大都采用多扫描链结构设计,因此又有一些适用于多扫描链结构的编码压缩方法被提出,如基于字典压缩的方法[7−9]、扫描切片重叠压缩方法[10,11]等。同时为了减少测试功耗,近年来不断有学者提出一些新的压缩方法和结构[12−14]。
扫描切片重叠压缩方法[10]是利用扫描切片的相容性来缩减测试数据。该方法只采用了单一的参考切片,因此参考切片的替换频率较高,限制了压缩率的提高和测试时间的减少。本文提出了一种基于镜像对称参考切片的多扫描链数据压缩方法,采用了两个相互镜像对称的参考切片,可以提高扫描切片与参考切片的相容概率,减少参考切片的替换频率。虽然镜像对称参考切片在编码时需要增加额外的编码码字,但是能够提高相容的概率,对于扫描链条数很多的现代SoC而言,这种方法能有效提高测试数据压缩率。为了叙述方便,将本压缩方法称为MSRS(Mirror Symmetry Reference Slices)方法。
2 MSRS方法设计
扫描切片重叠是指相邻扫描切片之间满足相容关系。两个N位的扫描切片(u1,u2,…,uN)和(v1,v2,…,vN)正向相容,当且仅当ui和vi的值相同或者它们中至少有一个是X位。如图1所示,测试向量包含10个扫描切片。每个切片包含4位。在原始扫描切片中第1个切片和第2个切片分别为{{1 X X 1},{X X 1 1}},这两个切片满足相容条件,因此这两个扫描切片重叠。统计发现一些ISCAS'89基准电路的MINTEST测试集中都含有大量的X位,所以扫描切片重叠的概率可能很高。扫描切片重叠压缩方法就是根据这一特点而提出的压缩方法。

图1 测试向量切片重叠
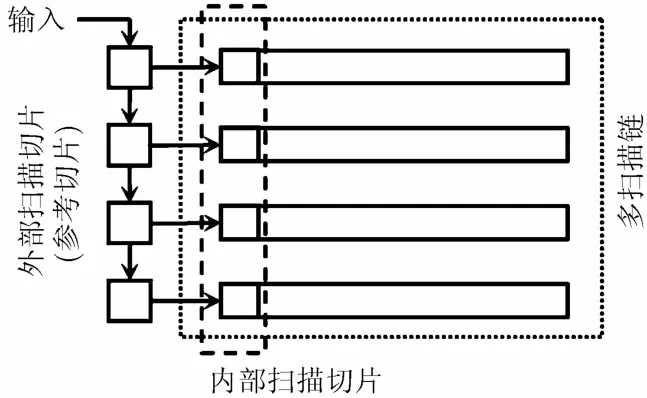
图2 扫描切片重叠结构
如果出现连续的扫描切片重叠,则一个快速将扫描切片移入扫描链的方法就是将重叠的第1个扫描切片串行输入到增加的外部扫描切片中,并锁定这个扫描切片。在接下来的时钟周期,只需要从这个外加的扫描片中将数据并行输入到内部扫描切片,这样可以大大减少冗余的时钟周期。该结构如图2所示,内部4条扫描链并行连接到一个外部扫描切片上,这个外部扫描切片也称之为参考切片。如果采用扫描切片重叠方法,对于图1中填充后的扫描切片,第1个扫描切片串行载入参考切片,再把参考切片并行载入扫描链;第2,第3个扫描切片与参考切片相容,直接把参考切片并行载入扫描链。第4个扫描切片与参考切片不相容,因此先把第4个扫描切片串行载入外部扫描切片,替换上一个参考切片,再并行载入扫描链。第5,第6,第7个扫描切片可以直接把参考切片并行载入扫描链。整个测试集中的10个扫描切片只有3个切片需要串行载入参考切片,其他的都可以并行载入。
2.1 MSRS压缩框架
MSRS方法中设置了两个镜像对称的参考切片,扫描切片可以同时与两个参考切片做正(反)向相容比较。这样大大增加了扫描切片与参考切片的相容概率。只要发生相容,就可以将参考切片直接并行载入内部扫描切片,不需要从外部串行载入。不仅减少了扫描周期,也减少了输入到外部扫描切片的数据。当然,我们也需要增加额外的编码码字表示不同的相容情况。
MSRS方法的压缩框架如图3所示。假定被测电路含有N条扫描链,镜像对称的参考切片RS1、RS2分别存储在两个移位寄存器中。假设RS2中的数据为(r1,r2,…,rN),则对应的RS1中数据为(rN, rN−1,…,r1)。我们将RS2参考切片称为原参考切片,RS1参考切片称为镜像参考切片。当扫描切片与参考切片相容时,把对应的参考切片移入扫描链。当扫描切片与参考切片不相容时,先将扫描切片移入两个寄存器中替换参考切片,然后再将替换后的原参考切片移入扫描链。MUX为二路选择器,用来选择哪一个参考切片被送入扫描链,随后的异或门用来选择正反向相容。参考切片选择信号和正反向相容选择信号都由有限状态机(Finite State Machine, FSM)提供。
2.2 参考切片更新与替换
当扫描切片与参考切片相容时,根据相容关系对参考切片中无关位X进行选择填充的过程称为参考切片更新。为了叙述方面,进行如下定义:
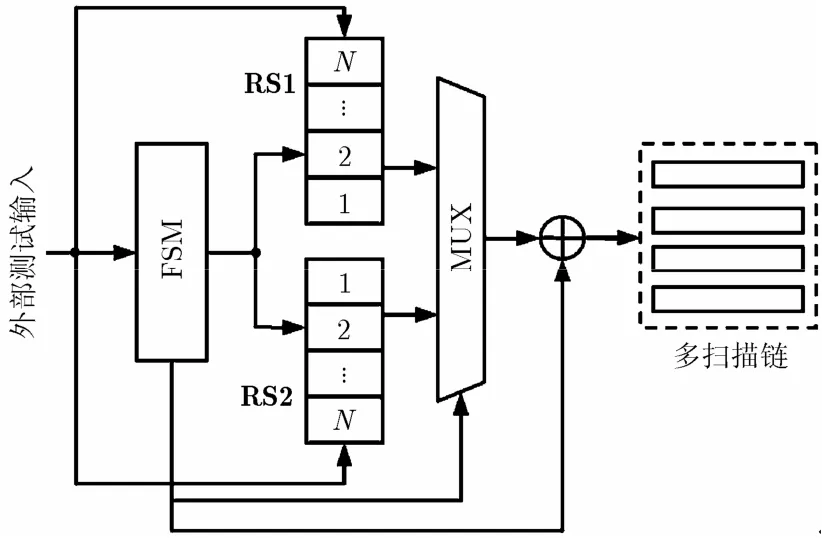
图3 MSRS压缩结构原理图
对长度为N的扫描切片a=(a1,a2,…,aN),定义
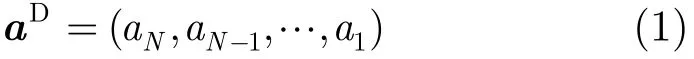
根据文献[15],定义测试数据0, 1, X求交(∩)、求反(!)运算规则

当扫描切片SSi与原参考切片RS2i相容时,原参考切片RS2i被移入扫描链,同时更新参考切片RS2i+1=RS2i∩SSi(正向相容)或RS2i+1=RS2i∩(!SSi)(反向相容),RS1i+1=RS2。当扫描切片SSi与镜像参考切片RS1i相容时,镜像参考切片RS1i被移入扫描链,同时更新参考切片RS1i+1=RS1i∩SSi(正向相容)或RS1i+1=RS1i∩(!SSi)(反向相容),RS2i+1=RS1。当扫描切片SSi与两个参考切片都不相容时,替换两个参考切片RS2i+1=SSi, RS1i+1= SSiD,然后将原参考切片RS2i移入扫描链。
2.3 最长相容策略
根据Huffman编码原理,通过对扫描切片与参考切片不同相容情况的出现频率进行统计,构造出一种编码规则,如表1所示。扫描切片与原参考切片正向相容,用标识位“0”表示;扫描切片与原参考切片反向相容,用标识位“1110”表示;扫描切片与两个参考切片都不相容的情况,用标识位“10”表示,并且在后面附加N位的当前扫描切片;扫描切片与镜像参考切片正向(反向)相容,用标识位“110”(“1111”)表示。
当扫描切片与参考切片只有一种相容情况时,可以直接确定编码码字、更新参考切片。但是当扫描切片与参考切片同时满足多种相容情况时,选择哪种相容情况来确定编码码字、更新参考切片对压缩结果有直接影响。假设当前的原参考切片RS21=“11X10XXX”,镜像参考切片RS11=“XXX01X 11”,当前扫描切片SS1=“1XXXXX11”,下一个扫描切片SS2=“1XX1XX01”。不难发现,SS1与RS21、RS11都正向相容。如果选择SS1与RS21正向相容,编码为“0”。参考切片更新为RS22=“11X10X11”, RS12=“11X01X11”。接下来扫描切片SS2与RS22、RS12做相容比较,发现不相容。SS2只能编码为“101XX1XX01”,同时替换参考切片。如果一开始选择SS1与RS11正向相容,编码为“110”。参考切片更新为RS2*2=“11X10XX1”, RS2*1=“1XX01 X11”。下一个扫描切片SS2与RS2*2正向相容,编码为“0”。显然,后者的压缩率更高。因此,当扫描切片与参考切片满足多种相容情况时,应该考虑参考切片与接下来的扫描切片之间的相容性,使之后尽可能多的扫描切片与参考切片相容,减少替换操作的发生。

表1 编码规则
MRSR方法采用的策略是以一个刚替换的参考切片为根节点,将扫描切片与参考切片不同相容情况用树节点的方式表示,一个扫描切片的不同相容节点处于树形结构的同一层,不同相容情况下更新的参考切片以及编码码字分别记录在对应的节点中,接着取下一个扫描切片分别与上一层中不同相容节点的参考切片做相容比较,若仍然存在相容的节点则继续取下一个扫描切片,若不存在相容的节点则说明这棵相容树构建完成,替换参考切片作为下一棵树的根节点。一旦构建完成一棵相容树,就采用广度优先搜索对这棵树进行遍历,找出从树根到最后一个相容扫描切片的最少编码码字的路径。为了防止计算量过于庞大,将相容树的最大深度限制为15。若达到最大深度,仍然有节点与参考切片相容,先找出这棵树的最少编码码字路径,以最短路径上的叶子节点作为下一个树的根节点。全为无关位的扫描切片可以直接填充,因为全为无关位的扫描切片总是可以选择最短编码码字的相容情况,并且不需要更新参考切片。我们将这个策略称为最长相容策略(Longest Compatibility Strategy, LCS)。通过图4所示相容树做进一步说明,RS2 (!RS2)表示扫描切片与原参考切片正(反)向相容,RS1(!RS1)表示扫描切片与镜像参考切片正(反)向相容。扫描切片SS1与根节点参考切片满足3种相容情况,产生3个节点!RS21, RS11, !RS11。下一个扫描切片SS2与节点!RS21中的参考切片满足两种相容关系,与节点!RS11中的参考切片也满足两种相容关系,与节点RS11不相容,扫描切片SS2总共产生4个节点。同理下一个扫描切片SS3与SS2产生的节点做相容比较,产生3个相容节点。扫描切片SS4与上一层的节点做相容比较,产生2个相容节点。扫描切片SS5与扫描切片SS4产生的两个节点都不相容,替换参考切片作为下一个相容树的根节点。从扫描切片SS1到SS4有两条路径,一条为1➙5➙9➙11,根据编码规则,总共需要12位码字;另一条为3➙7➙10➙12,需要16位码字。因此,最终选择第1条路径完成扫描切片SS1到SS4的编码。
2.4 编码压缩流程
我们以表2所示为例介绍MRSR方法的编码压缩流程。这里,SSi表示当前扫描切片,RS2i和RS1i分别表示原参考切片和镜像参考切片,每个切片都包含8位。Ei表示编码后对应的码字。
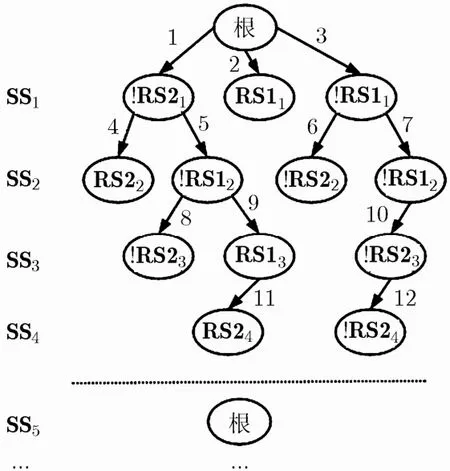
图4 相容树结构
编码开始,扫描切片SS1=“11X10XXX”,参考切片RS21=RS11=“00000000”。扫描切片SS1与参考切片RS21, RS11不相容,替换参考切片RS22= SS1=“1X1XX0XX”, RS12=SS1D=“XX0XX1 X1”。采用最长相容策略确定扫描切片SS2, SS3, SS4与参考切片的相容关系,并根据编码规则对扫描切片进行编码。根据参考切片RS25=“11X10101”,扫描切片SS1的编码结果E1=“1011X10101”。扫描切片SS5=“01XXXX1X”与RS25, RS15都不相容,替换后参考切片RS26=SS5=“01XXXX1X”, RS16=S=“X1XXXX10”。扫描切片SS=“X10XX
6XX1”只与RS26正向相容,SS6编码结果E6=“0”。更新参考切片RS27=“010XXX11”,RS17=“11XX X010”,扫描切片SS5的编码结果E5=“10010XXX 11”。至此,6个扫描切片的测试数据全部编码完成。编码后的码字中仍然含有无关位X,为了减少测试功耗,可以采用随机填充或者相邻填充(adjacent filling)[15]方法。未压缩的源测试集需要存储48 bit,压缩后只需要存储29 bit。只有2个扫描切片需要串行加载,其它4个扫描切片可以并行加载。
3 解压器设计
MSRS方法的解压器结构如图5所示,整个电路由FSM模块、计数器模块、门控时钟模块、镜像对象参考切片、多路选择器和异或门阵列组成。
当解压器使能信号“Dec_en”为“1”, “Data_ in”端口开始接收数据。若扫描切片与参考切片不相容,参考切片需要更换。此时,“inc”信号为“1”,“shift”信号为“1”,“ssen”信号为“0”。计数器开始计数,“Data_rs”端将输入数据移入参考切片。当计数到N个时钟周期时,“rst”信号被置为“0”,“inc”,“shift”,“ssen”信号的值翻转。一个扫描切片的输入数据完全移入参考切片,被测电路将相应的数据移入扫描链。若扫描切片与参考切片正向相容则“xor”信号为“1”,反向相容“xor”信号为“0”。“select”信号为“1”则选择镜像参考切片载入扫描链,“select”信号为“0”则选择原参考切片。

表2 编码压缩流程

图5 解压器结构
FSM状态转换如图6所示。S0是初始状态,根据编码规则,当“Data_in”输入为“0”时,表示扫描切片与原参考切片正向相容,FSM状态保持不变。当“Data_in”输入为“1”时,FSM转入S1状态,若“Data_in”的下一时钟周期输入为“0”,表示扫描切片与参考切片不相容,经过N个时钟周期后,完成参考切片的更换,FSM进入S0状态;若“Data_in”输入为“1”,FSM从S1状态转入S2状态。接下来,若“Data_in”的下一时钟周期输入为“0”,表示扫描切片与镜像参考切片正向相容,FSM进入S0状态;若Data_in输入为1,FSM从S2状态转入S3状态。最后,FSM始终执行从S3状态转入S0状态。若“Data_in”的下一个时钟周期输入为“0”,表示扫描切片与原参考切片反向相容;若“Data_in”输入为“1”,表示扫描切片与镜像参考切片反向相容。需要说明的是,MSRS方法中只有原参考切片RS2需要外部寄存器存储,镜像参考切片RS1并不需要直接存储,而是通过对原参考切片RS2寄存器组进行硬布线的方式产生。
4 实验结果与数据分析
为证实MSRS方法的有效性,对ISCAS'89中的部分大电路进行了实验,各电路的测试激励数据由MINTEST生成。MSRS方法的压缩结果如表3所示,其中TD是原始测试集大小,TE是压缩后测试集大小,#sc是划分的扫描链数量,CR是数据压缩率,CT是时间压缩率。从表3中可以看出,时间压缩率CT比数据压缩率CR大,这是因为采用最长相容策略使相容情况尽量增加,而出现相容时只需要一个时钟周期就可以将参考切片并行送入多扫描链,因此大大减少了测试时间。

图6 FSM状态转换
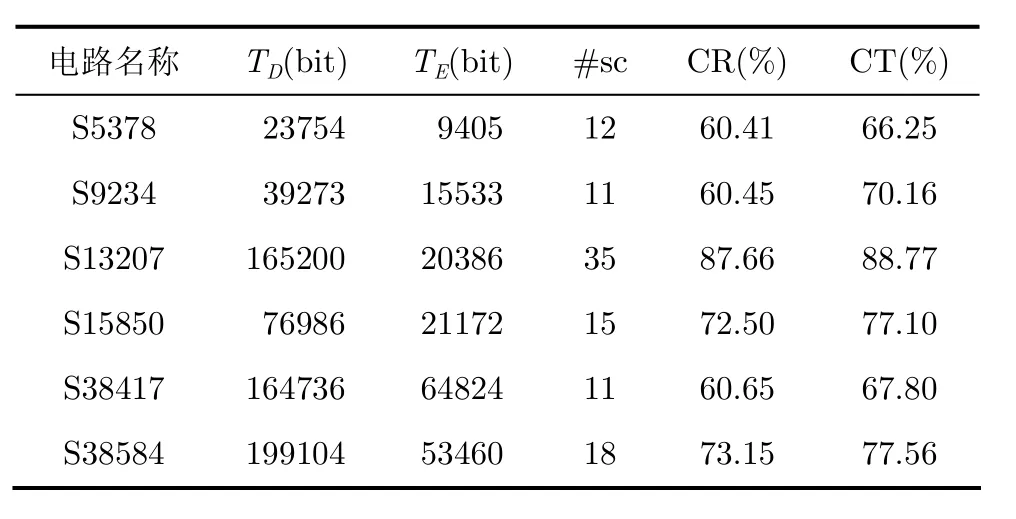
表3 MSRS方法压缩结果
表4所示为MSRS方法与单扫描链压缩方法的比较,第1列为电路名称,第2列到第5列分别为FDR[2], VIHC[3], SRLC[5]和OSHC[4]的压缩率,最后一列为本文方法的压缩率。从实验结果可以看出,MSRS方法中只有电路S38417的压缩率低于其他方法,这是由电路S38417测试集的数据特征决定的。一方面是因为电路S38417测试集中无关位X的比例只有68%,是所有实验电路中最低的;另一方面是因为电路S38417测试集中相邻切片间的相容性较差,参考切片需要经常替换。由于这两方面的影响导致电路S38417的压缩率低于其他方法。在平均压缩率方面,MSRS方法比FDR码高11.92%,比VIHC码高8.13%。
表5所示为MSRS方法与其他多扫描链压缩方法的比较,#sc表示划分的扫描链数量,CR表示百分比压缩率。文献[11]中方法只采用了一个参考切片。文献[12]中提出了扫描切片之间的多层复制方法。本文的方法采用了两个参考切片,采用最长相容策略,平均压缩率比文献[11]高6.01%,比文献[12]高1.94%。
测试功耗是集成电路测试技术中另一个重要的问题。我们采用电路的加权跳变度量[16](WeightedTransition Metric, WTM)模型来评估功耗。设扫描链长度为l,测试向量tj=(aj,1,aj,2,…,aj,l),则向量tj的WTM值为
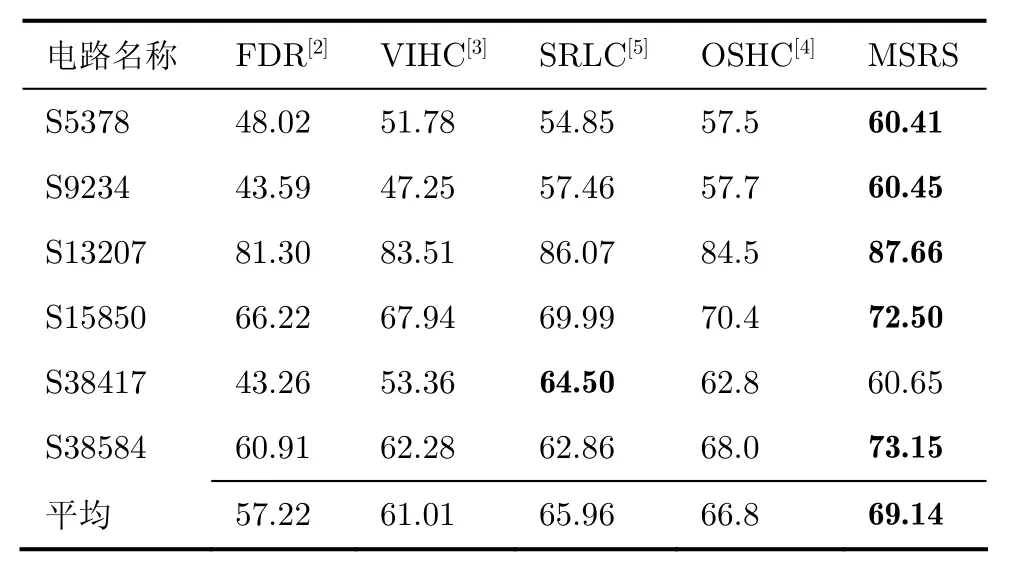
电路名称 FDR[2]VIHC[3]SRLC[5]OSHC[4]MSRS S5378 48.02 51.78 54.85 57.5 60.41 S9234 43.59 47.25 57.46 57.7 60.45 S13207 81.30 83.51 86.07 84.5 87.66 S15850 66.22 67.94 69.99 70.4 72.50 S38417 43.26 53.36 64.50 62.8 60.65 S38584 60.91 62.28 62.86 68.0 73.15平均 57.22 61.01 65.96 66.8 69.14
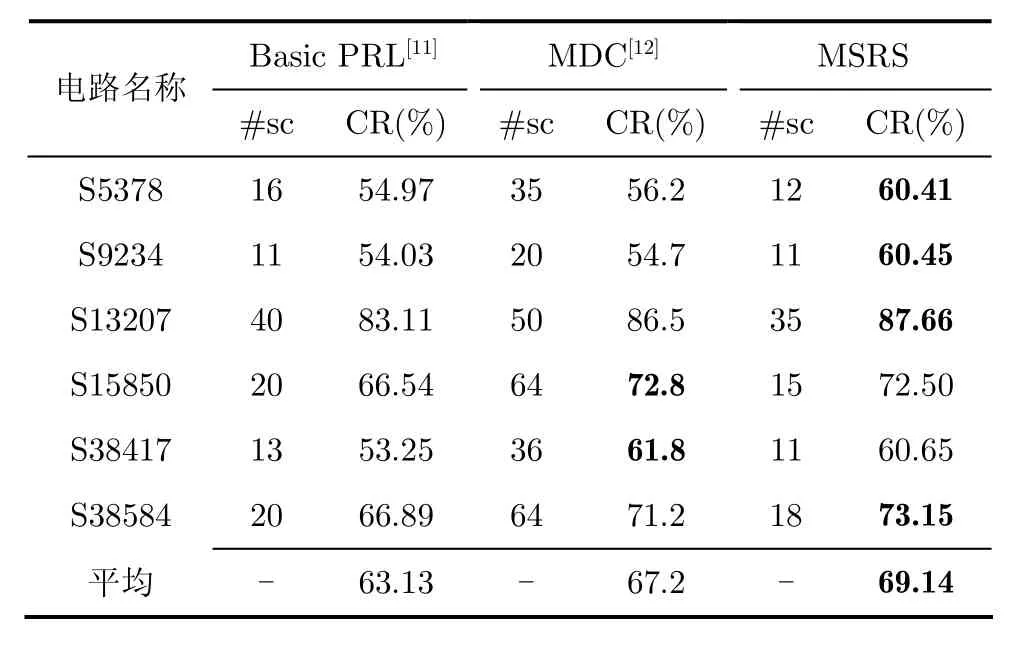
表5 MSRS方法与多扫描链压缩方法的比较
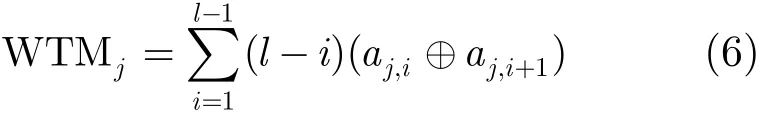
对于含有n个测试向量的测试集,其平均功耗WTMavg和峰值功耗WTMpk分别为

针对MINTEST测试集,表6列出了FDR编码与MSRS方法的测试功耗比较结果。FDR编码的测试功耗是MSRS方法的13倍之多,这是由于MSRS方法采用的是多扫描链结构,缩短了扫描链长度,使得功耗计算公式中的权值(l−i)大大减小。MSRS方法作为一种多扫描链压缩方法,在测试功耗方面与单扫描链压缩方法相比有明显优势。
5 结论
针对近年来集成电路测试中测试数据显著增加的问题,本文提出一种基于镜像对称参考切片的多扫描链数据压缩方法。该方法充分利用了扫描切片与参考切片之间的相容性,采用两个相互镜像对称的参考切片与扫描切片做相容性比较,从而提高了扫描切片与参考切片的相容概率,减少了参考切片的替换频率。不仅取得了较高的压缩率,而且大大减少了测试应用时间和测试功耗。
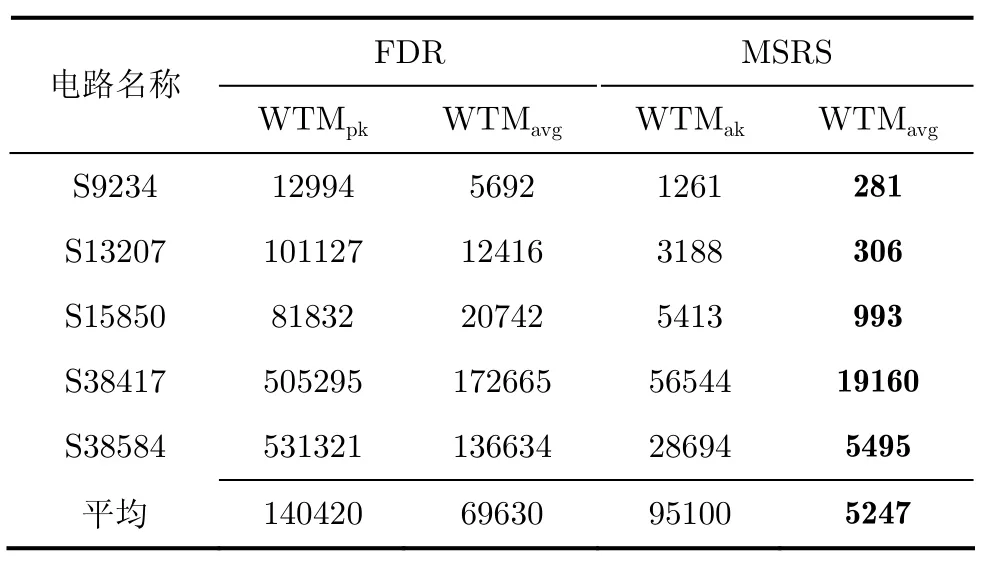
表6 测试功耗比较(加权跳变度量)
[1] Touba N A. Survey of test vector compression techniques[J]. Design & Test of Computers, 2006, 23(4): 294-303.
[2] Chandra A and Chakrabarty K. Test data compression and test resource partitioning for system-on-a-chip using frequency-directed run-length (FDR) codes[J]. IEEE Transactions on Computers, 2003, 52(8): 1076-1088.
[3] Gonciari P T, AI-Hashimi B M, and Nicolici N. Variablelength input huffman coding for system-on-a-chip test[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2003, 22(6): 783-789.
[4] Kavousianous X, Kalligeros E, and Nikolos D. Optimal selective huffman coding for test-data compression[J]. IEEE Transaction on Computers, 2007, 56(8): 1146-1152.
[5] 詹文法, 梁华国, 时峰, 等. 一种共游程码的测试数据压缩方法[J]. 计算机研究与发展, 2008, 45(10): 1646-1653.
Zhan Wen-fa, Liang Hua-guo, Shi Feng, et al.. A scheme of test data compression based on sharing run length code[J]. Journal of Computer Research and Development, 2008, 45(10): 1646-1653.
[6] 马会, 邝继顺, 马伟. 基于一位标识的测试向量混合编码压缩方法[J]. 电子测量与仪器学报, 2013, 27(4): 312-318.
Ma Hui, Kuang Ji-shun, and Ma Wei. Hybrid coding compression method of test vector based on an identification [J]. Journal of Electronic Measurement and Instrument, 2013, 27(4): 312-318.
[7] Sismanoglou P and Nikolos D. Input test data compression based on the reuse of parts of dictionary entries: static and dynamic approaches[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2013, 32(11): 1762-1775.
[8] Sismanoglou P and Nikolos D. Test data compression basedon reuse and bit-flipping of parts of dictionary entries[C]. Proceedings of 17th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Warsaw, Poland, 2014: 110-115.
[9] 刘杰, 易茂祥, 朱勇. 采用字典词条衍生模式的测试数据压缩[J]. 电子与信息学报, 2012, 34(1): 231-235.
Liu Jie, Yi Mao-xiang, and Zhu Yong. Test data compression using entry derivative mode of dictionary[J]. Journal of Electronics & Information Technology, 2012, 34(1): 231-235.
[10] Han Yin-he, Hu Yu, Li Hua-wei, et al.. Ripad and energyefficient testing for embedded cores[C]. Proceedings of 13th IEEE Asian Test Symposium, Washington DC, USA, 2004: 8-13.
[11] Ruan X and Katti R. An efficient data-independent technique for compressing test vectors in systems-on-achip[C]. Proceedings of IEEE Computer Society Annual Symposium on Emerging VLSI Technologies and Architectures, Karlsruhe, Germany, 2006: 153-158.
[12] Lin Shih-ping, Lee Chunag-len, Chen Jwu-e, et al.. A multilayer data copy test data compression scheme for reducing shifting-in power for multiple scan design[J]. IEEE Transactions on Very Large Scale Integration(VLSI) Systems, 2007, 15(7): 767-776.
[13] Tyszer J, Filipek M, Mrugalski G, et al.. New test compression scheme based on low power BIST[C]. Proceedings of 18th IEEE European Test Symposium, Avignon, France, 2013: 1-6.
[14] Chloupek M, Jenicek J, Novak O, et al.. Test pattern decompression in parallel scan chain architecture[C]. Proceedings of 16th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Karlovy Vary , Czech Republic, 2013: 219-223.
[15] Yi Mao-xiang, Liang Hua-guo, Zhang Lei, et al.. A novel x-ploiting strategy for improving performance of test data compression[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2010, 18(2): 324-329.
[16] Sankaralingam R, Oruganti R P, and Touba N A. Static compaction techniques to control scan vector power dissipation[C]. Proceedings of IEEE VLSI Test Symposium, Montreal, Canand, 2000: 35-40.
邝继顺: 男,1959年生,博士,教授,研究方向为集成电路测试与设计、嵌入式系统.
刘杰镗: 男,1989年生,硕士,研究方向为集成电路测试.
张 亮: 男,1989年生,硕士,研究方向为集成电路测试.
Test Data Compression Method for Multiple Scan Chain Based on Mirror-symmetrical Reference Slices
Kuang Ji-shun Liu Jie-tang Zhang Liang
(College of Information Science & Engineering, Hunan University, Changsha 410082, China)
In order to reduce test data and test time, a test data compression method for multiple scan chain which bases on mirror-symmetrical reference slices is proposed. This method uses two mutually mirror-symmetrical reference slices for compatibility comparison with scan slice, that improves the compression ratio. If the scan slice is compatible to one of the reference slices, only a few bits are needed to encode it and can be loaded in parallel. Otherwise, the scan slice will replace one reference slice. A longest compatibility strategy is proposed when the scan slice and reference slice satisfy more compatible relationship. It can further improve the test compression ratio to determine the code word according to the different compatibility frequency statistics situations. The experimental results show that the average compression rate of the proposed scheme reaches 69.13%.
Test data compression; Multiple scan chain; Compatibility; Reference slice; Scan slice
TP302
: A
:1009-5896(2015)06-1513-07
10.11999/JEIT141146
2014-09-02收到,2014-12-23改回
国家自然科学基金(61472123, 60673085)资助课题
*通信作者:刘杰镗 liujietang126@163.com

