基于两杆张拉整体结构的可展机构设计*

孙建伟，赵浩然，孙金荣

（1.长春工业大学机电工程学院，长春130012；2.钱潮轴承有限公司智造工程中心，杭州311215）

0 引言

在航空航天工程技术的发展中，由于运载火箭的储存空间有限，在设备未到达工作位置时，应当以较小的体积储存运输，当到达指定工作地点时，能进行展开，并保持稳定，所以可展机构得以大力发展[1-2]。常见的可展机构分为一维的伸展臂结构、二维的星载平面天线结构以及三维的空间可展开天线结构[3-5]。其中圆形可展开结构是空间可展开天线结构的主要表现形式，最早的固体反射面可展天线[6]由美国的TRW公司研制的Sunflower空间可展天线，展开状态为空间抛物面，收拢时为圆柱形。

近年来，中国地质大学的丁华锋团队[7-8]对伞状可展机构进行了研究，通过一类双层双环的连杆结构建立了可展机构的可展单元，再通过结构拓扑获得了一系列的伞状可展机构。胡甜甜[9]根据星载可展天线提出了一种设计方案，并对其方案进行了ADAMS仿真分析。

张拉整体结构[10]是由美国建筑大师富勒（R B Full⁃er）提出的，最早应用于建筑方面，由于张拉整体结构与传统刚性结构不同，具有自平衡、可变形等优点，与可展机构具有相似的特性，为本文的可展机构的设计提供了新的设计灵感。Liu等[11]分析了轴向拼接张拉整体单元的方法，通过两个三杆张拉整体结构拼接成球形张拉整体机器人。Nagasea等[12]利用相同的张拉整体单元，结合连接矩阵，构建复杂张拉整体结构的系统化建模方法。Sulatan[13]通过对拉索长短的变化控制张拉整体的展开，并分析了由上下两层张拉整体组成的可展机构的展开路径。Tibert等[14]将六棱柱张拉整体作为基本单元，设计并制作了可展天线，可应用于小型卫星。

本文的主要研究目标是将平面两杆张拉整体的结构特点应用于可展机构的设计，基于平面两杆张拉整体结构的自平衡、自稳定的优点，对可展机构进行几何参数设计，使机构具有可展机构的功能同时可以快速展开，并在展开到稳定状态时，能够具有一定的稳定性。

1 可展单元设计与分析

1.1 可展机构单元设计

张拉整体结构是一些离散的受压构件包含于一组连续的受拉构件中形成的稳定自平衡结构。两杆张拉整体结构是最基本的平面张拉整体结构，通过改变张拉整体结构中拉簧与受压杆的相对位置关系提出一种由张拉整体结构组成的可展单元结构。图1（a）所示为平面两杆三索张拉整体结构，将平面两杆三索张拉整体结构中两个受压杆下端A、B向中间靠拢铰接于一点，弹簧DE、CF位置保持不变得到图1（b）。将此张拉整体结构应用到可展机构中，作为可展机构的可展单元使用。由于张拉整体结构具有可变形、自适应、自稳定、柔性的特点，所以作为可展单元时，相对于目前的可展机构，可以使可展机构具有快速展开并保持稳定的特点。

图1 可展单元结构变化过程

1.2 两杆张拉整体结构找形

图2 所示为两杆张拉整体的结构简图。由2根受压杆AC、BD和3根受拉弹簧ED、DC、CF组成。杆AC、BD的长度分别为LAC、LBD。弹簧DE、CF固定于点E、F，EF的长度可以调整，令EF=ρ，且AE和AF距离相等。弹簧ED、DC、CF的长度分别为LED、LDC、LCF，弹簧刚度系数为K。C、D两点的高度y相同，并且∠DAE=∠CAF=θ。机构自由度F=1，机构形状由广义坐标参数θ决定。

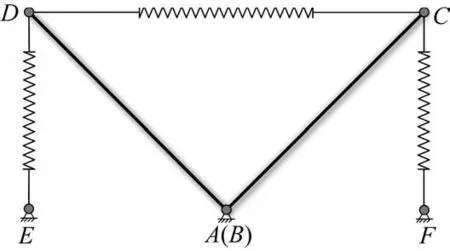
图2 两杆张拉整体结构

通过对提出的可展单元，即平面两杆张拉整体进行找形分析，把ρ看作输入，把y看作输出，不同的ρ值对应不同的y。通过输出参数即弹簧稳定时的长度y，证明张拉整体结构存在自稳定平衡状态，进而得出可展单元自稳定平衡状态时的几何参数与尺寸参数。

根据结构的几何关系可得弹簧长度：

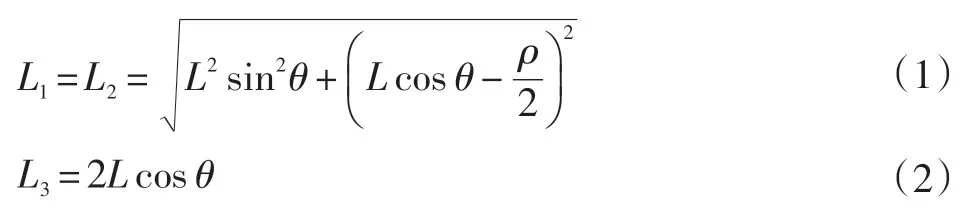
机构的势能（重力忽略）为：

根据最小势能原理得：

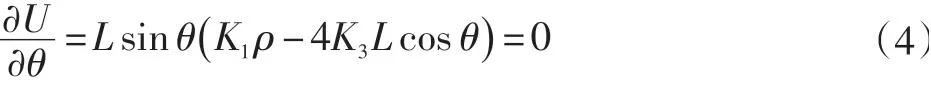
由式（4）可得：

通过式（5）可以求解广义坐标θ的值，以此来确定结构的形状。

1.3 两杆张拉整体结构奇异性分析

将式（5）代入y=Lsinθ得：

为了证明一个结构是否存在奇异性，因此对结构进行奇异性分析很有必要。奇异性分析的数学描述是：“一个结构或者系统的奇异构型对应其雅可比矩阵J的行列式等于零、趋于无穷、或者是不确定的情况。”本结构中只有一个输入参数，故雅可比矩阵是一个标量数。

由式（8）可推出：

由式（6）和式（9）得：

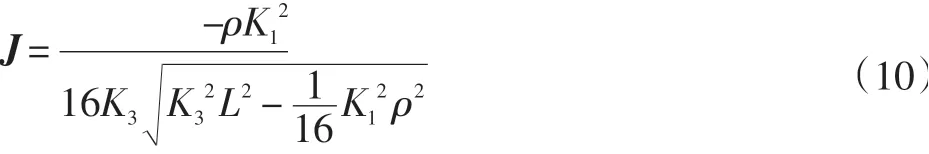
为了研究机构的奇异形，将雅可比矩阵分解为两部分。

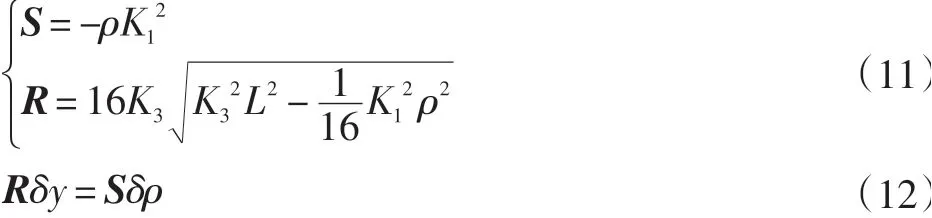
该张拉整体结构的奇异形对应着R=0或S=0的情况，这时ρ=4K3L/K1或ρ=0。当ρ=0时，y=L，此时两杆重叠并垂直X轴。当ρ=4K3L/K1时，y=0，此时两杆共线并垂直Y轴。为避免奇异形，所以ρ的取值范围为0＜ρ＜4K3L/K1。

2 可展机构的运动学分析

2.1 可展机构几何参数设计

可展机构在完全收拢、逐渐展开到完全展开的过程中，机构的每个可展结构单元相对于底座机架都具有相同运动状态。因此选择机构中任意两个连接的可展单元，通过底座机架为正六边形的性质，可以得出可展机构完全展开状态下的机构参数，图3所示为可展机构完全展开状态下的参数模型。

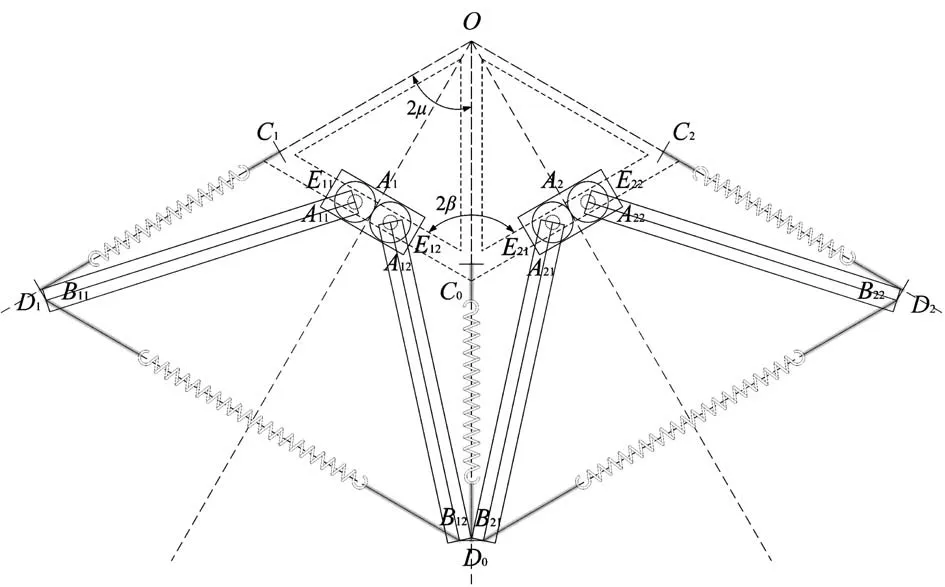
图3 可展机构的参数模型

O为 机 架 重 心，C1、C0、C2为 机 架 的 顶 点，C1C0、C0C2为机架的边。OA1⊥C1C0、|C1A1|=|A1C0|、OA2⊥C0C2、|C0A2|=|A2C2|。∠C1OC0=∠C0OC2=2μ，为机架的边对应的圆心角，2β为机架相邻两边的夹角，OC0为2β的角平分线，∠C1C0O=∠OC0C2=β。C1D1、C0D0、C2D2为受拉构件（弹簧）分别与OC1、OC0、OC2共线；A11B11、A12B12、A21B21、A22B22分别为受压构架（杆）；杆的一端A11、A12、A21、A22连接在机架上，由齿轮E11、E12、E21、E22完成同步展开收拢功能，其中|A11A1|=|A1A12|、|A21A2|=A2A22|。C1D1D0C0、C0D0D2C2分别为相邻的两个可展单元，相邻的两个可展单元共用受拉构件（弹簧）C0D0。

根据前文对张拉整体结构的分析及计算，设计得到可展机构的尺寸参数如表1所示。

表1 可展机构尺寸参数表

2.2 可展机构运动学模型分析

本文中，运用传递矩阵法对所设计的可展机构进行运动学分析，如图4所示，建立空间直角坐标系。其中Σ0O0-x0y0z0为全局坐标系；ΣiOi-xiyizi（i=1,2,…,6）为每个可展结构单元所对应的局部坐标系。局部坐标系Σi相对于全局坐标系Σ0的旋转角度为：即：

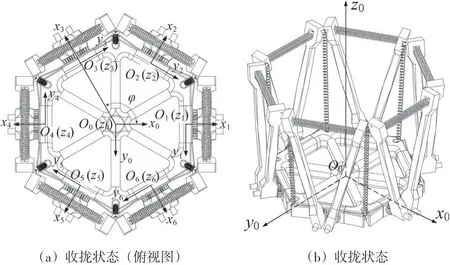
图4 可展机构

与底座转轴相连的为转动套筒，α为转动套筒的转角，转动套筒的角速度为：

转动套筒初始相位角为0，转角α为：

对t进行二阶求导，得到转动套筒的角加速度为：

2.3 可展机构运动学分析

在各个局部坐标系Σi中，均有两个关于xiOizi面对称的受压杆件，在此分析杆件末端坐标x为正的受压杆件。可展机构中受压杆件i（i=2,…,6）的转动角度与转动套筒的转动角度相同，范围为α∈[0,π/2]，各个局部坐标系Σi相对于全局坐标系Σ0的齐次变换矩阵为：

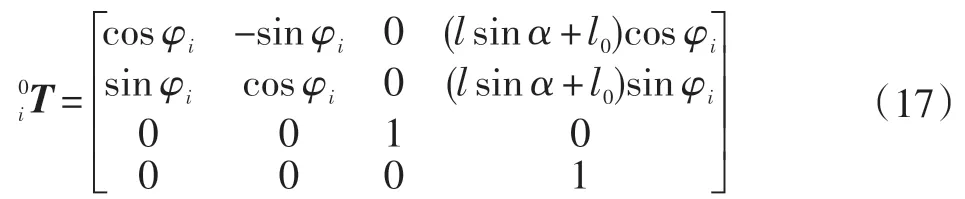
任意局部坐标系Σj与全局坐标系Σ0的齐次变换矩阵的关系式为：

由公式：

得到该时刻点N在全局坐标系Σ0中的坐标列矢量0N，由此可得点N在全局坐标系Σ0中相对于坐标原点O0的位移。

在任意时间点，可展机构的杆件末端点Ni（i=1,2,…,6）在与相应的局部坐标系Σi中的坐标列矢量为：

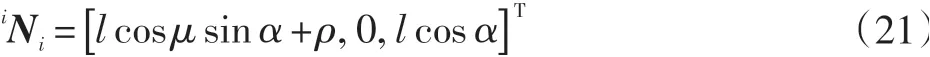
根据式（20）可得杆件末端点Ni（i=1,2,…,6）在全局坐标系Σ0中的坐标列矢量为：

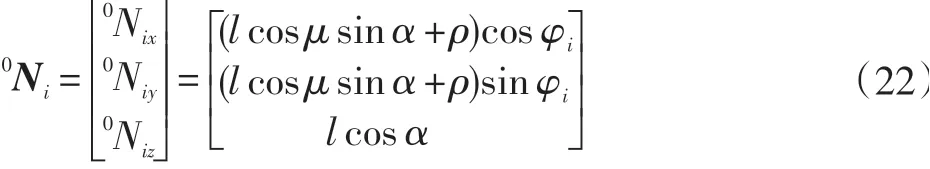
用si=[six,siv,siz]T表示点Ni在全局坐标系Σ0中相对于坐标原点O0的位移，则有si=0Ni。对时间t求一阶导数，可得点Ni在全局坐标系Σ0中的速度为：

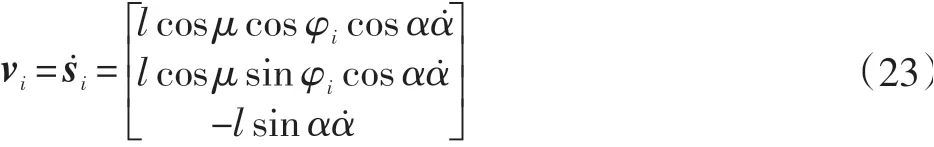
同理，对时间t求二阶导数，可得点Ni在全局坐标系Σ0中的加速度为：

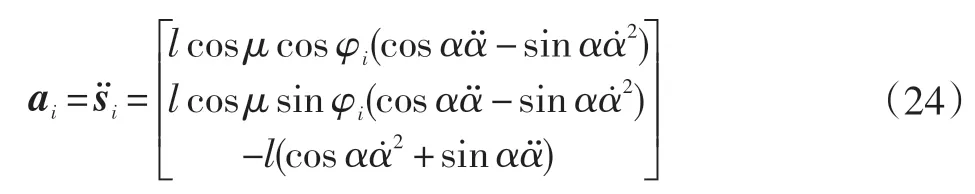
3 仿真分析及结果对比

3.1 MATLAB运动仿真分析

根据上述的运动学方程，将公式通过MATLAB编程，得到各受压杆件末端点Ni（i=1,2,…,6）在全局坐标系Σ0中的位移s、速度v、加速度a与时间t的关系曲线。其中位移、速度、加速度与时间的关系曲线分别如图5~7所示。

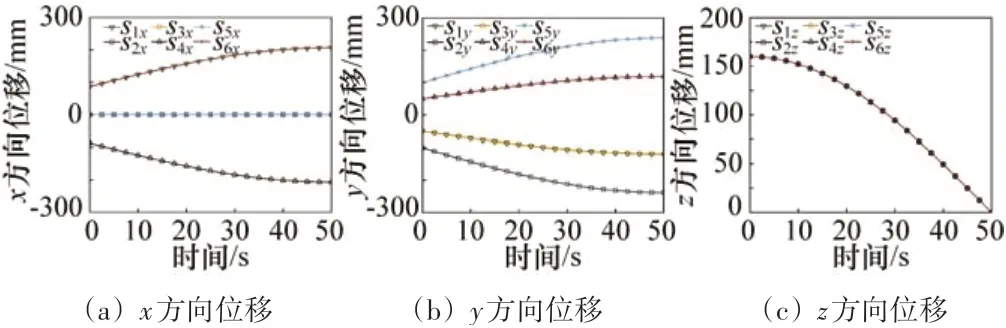
图5 末端点Ni的位移曲线

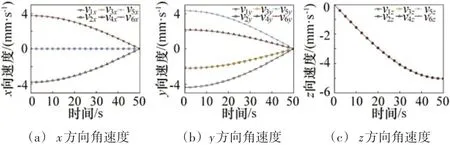
图6 末端点Ni的角速度曲线

图7 末端点Ni的加速度曲线

3.2 ADAMS运动仿真分析

基于张拉整体结构的可展机构模型以及相关尺寸参数建立可展机构ADAMS仿真模型并进行仿真试验，验证仿真模型能够实现可展机构的快速展开，观察可展机构从完全收拢到完全展开的全过程。基于ADAMS进行仿真分析，可得各个受压杆件末端点Ni在全局坐标系Σ0中位移、速度、加速度与时间的关系曲线如图8~10所示。

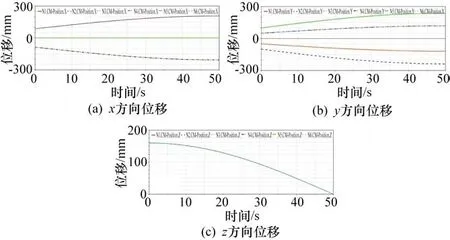
图8 末端点Ni的位移曲线

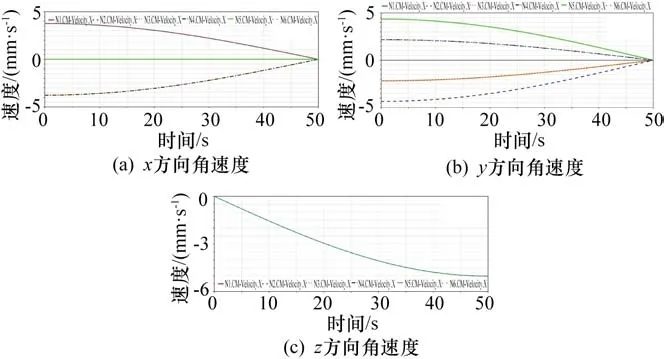
图9 末端点Ni的角速度曲线

图10 末端点Ni的角加速度曲线

通过仿真试验验证了样机模型能够实现可展机构的运动。从仿真分析结果可以看出受压杆件末端某一点的位移、速度、加速度与时间的关系理论计算结果和模型仿真结果大致相同。也可以看出可展机构能够有效的快速的展开，说明所提出的理论方法的有效性和计算的正确性。

4 可展机构的样机试制及展开实验

根据对可展机构的设计，通过3D打印技术搭建了可展机构的实物模型，用于验证可展机构的实际可行性。图11（a）所示为可展机构实物模型的完全收拢状态，图11（b）所示为可展机构实物模型的完全展开状态。机构的有效展开与收拢证明该可展机构的制造是可行的。

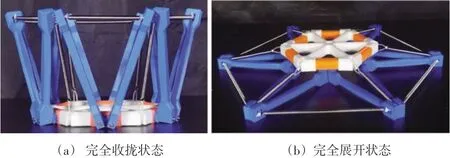
图11 可展机构的展开过程

5 结束语

本文提出了一种以平面两杆张拉整体结构作为可展单元结构的可展机构，该机构具有张拉整体结构的特性。基于平面两杆张拉整体结构模型，对可展单元结构进行找形分析，奇异性分析，得出可展单元结构的几何尺寸参数。通过三维仿真软件对建模好的可展机构进行运动学仿真，验证前文所提出的理论模型的合理性。通过3D打印机打印可展机构零件，并通过弹簧以及螺钉螺母紧固件进行拼装连接，通过实物模型的展收实验，验证前文提出机构的可行性。通过一系列的实验得出该机构理论实践均可行，可应用于航空航天中。