某机场安检通道的动态优化配置方法研究

汪春华，李泳懿，林家星，毛 宁

（广东工业大学机电工程学院，广州510006）

0 引言

空中客流量的迅速增加，给航空业发展带了新的挑战。机场安检过程相对复杂，往往需要排队等待，而安检更是国内机场离港流程中的瓶颈环节[1]，安检的效率往往影响旅客能否顺利出行及机场服务质量。

近些年来，国内外学者对于安检问题进行了大量相关研究。王睿明等[2]使用了标准M/M/1排队模型对机场值机柜台进行了数学建模与分析。蒋欣欣等[3]选择广义随机Petri网对航站楼内单通道安检服务流程进行建模与仿真分析。顾扬[4]用正态分布拟合旅客的等待时间，比较了不同人员配置对安检效率和成本的影响。杨媛元等[5]通过使用虚拟排队方法来均衡机场客流量。国外Ward Whitt[6]讨论了应对时变人员需求，利用逐点平稳近似的方法描述传统服务排队模型的性能。Linda V Green等[7]展示了在非平稳环境下使用平稳排队模型的方法。Wang等[8]建立了一个网络流结构，基于该思想将客流抽象为网络流，来分析国际机场安检吞吐量的瓶颈。

本文研究以某机场安检部旅检业务室作为背景，对旅客到达情况以及通道数开放情况进行研究。以大量历史数据为基础，构建安检通道优化模型并建立仿真平台，利用数学优化和仿真优化相结合的方法进行仿真实验，并对历史数据方案、数学优化方案和仿真优化方案的结果进行比较与评价，得到各时段安检通道的最优开放数量，有效提升人力资源的利用率。

1 安检旅检通道系统

本文所研究的旅检业务室，隶属于某机场T1航站楼。在T1航站楼，国内旅检通道区域分为东三和西区，其中该业务室所负责的东三安检区域有16条通道口，每个通道口由一个班组负责，每个班组6~7人。所有通道口的安检流程一样，安检效率等同。通常来说，每个旅客的服务时间是随机且独立的，且各个时段的旅客到达速率也不同。

由于每个通道口通过旅客数量有一定限额，当旅客集中到达时，容易导致旅客排队时间增加。为了体现机场的服务质量，遂提出一项规定，当某一通道口排队队列长度超过12人时，需要主动增开通道口，加快旅客消耗速率。当旅客到达明显减少时，该区域可酌情关闭通道口，释放一部分人力。经过调研过后得到的历史数据，在不同时段下东三区域的通道口数量的变化如表1所示。由表可知，在短短3 h内，通道口开放数发生较大的变化。如果单纯考虑旅客服务体验，开放过量安检通道口，会造成人力资源的浪费。但通道口开放数量过少，则会增加旅客的排队时间，降低旅客满意度。根据不同时间段的旅客到达情况，配置相应数量的通道口，是一个亟需解决的运筹优化问题。

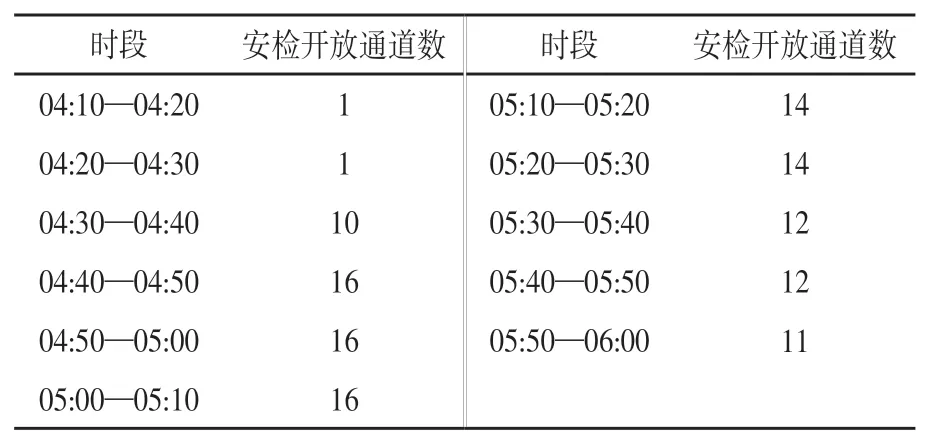
表1 某天东三区域04:00—06:00安检开放通道数

2 安检旅检通道配置优化模型的数据处理及其必要性

2.1 通道动态变化过程的时段平稳化处理

通过现场调研和分析历史数据进行分析，发现到达旅客量和安排开放通道数变化周期为天，且各个时期各个时段下安排开放通道数不太受特殊节假日的影响，故可只对每天进行计划通道配置，来动态调整实际开放通道来满足不同时段到达旅客的安检服务需求。

由于一天内到达的旅客流是随时间变化而变化的动态随机过程，且各个时段旅客到达速率波动明显，安检服务人员需要随着实际到达旅客数来实时开关通道来配置开放通道数，导致每天开放通道数也是一个动态配置过程。而现有数学工具和理论方法无法对动态随机过程进行精确求解和优化。

因此本文主要基于采用时段平稳化求解动态变化过程的思路，将时间分割成111个时段，每个时段为10 min，并将每个时段下的动态过程分别视为一个稳态的GI/G/m的单服务排队系统，建立的数学模型及仿真模型，求解111个时段的稳态单服务排队系统的平均等待时间、平均等待队长等指标，并与历史结果进行三者比较。时段平稳化求解动态变化过程流程如图1所示。

图1 时段平稳化求解动态变化过程流程

2.2 通道配置优化模型数据的必要性处理

通过对输入的实际数据进行必要性处理，根据核密度估计与卡方检验，对各个时段的样本使用非参数估计的核密度估计来拟合概率密度函数曲线，再用卡方检验的方法来验证拟合曲线的拟合度。通过拟合度检验后，一方面输出仿真模型输入的必要性参数（即旅客到达分布、服务时间分布等）；另一方面根据分段直方图法，通过输入各时分布及其概率密度函数，通过一系列的处理得出各时段的均值及标准差，并建立数学模型必要参数的计算方法，若通过面积极差偏差约束，则输出数学模型输入的必要性参数。模型必要参数检验流程如图2所示。

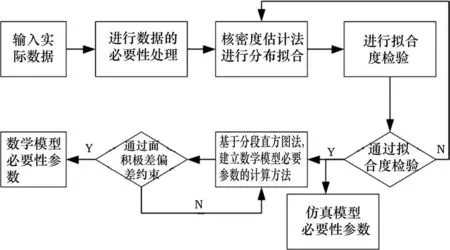
图2 模型必要参数检验流程

3 通道配置优化模型的建立及求解

由于旅客数量在不同时期、不同时段容易产生较大的差异，使得旅检通道配置更加复杂。对于解决该类问题，不能单纯通过增加资源投入来解决，要充分考虑到机场安检区域开放通道数的各种限制和到达旅客的排队舒适度。因此，现结合排队论相关理论，建立优化旅检通道配置数量的模型。该模型的特点是：（1）旅客间到达是独立的，旅客相继到达的间隔时间是随机的；（2）安检服务系统采取先到先服务的服务原则和等待制的排队规则；（3）旅客接受服务是各自独立且接受服务时间是随机的；（4）各个时段下的安检服务系统是相互独立的。

该模型的目标函数为开放旅检通道数最少，且经过调研后，发现模型必须遵循开放总通道数约束、平均等待时长约束和平均等待队长约束。建立如下旅检通道配置模型：

式中：ji为时段i下开放的通道数；Wˉi为第i个时段所有旅客的平均等待时间；Wˉub为最大平均等待时间；Qˉi为第i个时段下的平均等待队长；Qˉub为最大平均等待队长；ji为第i个时段开放的通道数；xij为时段i是否开放j个通道，xij=1为开放，xij=0为关闭；I为区域通道数总数。

在经过参数必要性处理后，利用相关排队论知识，通过枚举法求出不同时段下旅检通道最优配置数目，数学优化结果如表2所示。由表可知，经过数学模型优化过后，各个时段的安检通道口开放数较历史计划开放数都有了明显的降低。

表2 04:00—06:00各时段数学优化结果

4 仿真平台测试

4.1 平台搭建

在搭建仿真模型的过程中，通过前期调研和查阅国内外文献，每个时段下的事件流程为：旅客间独立随机到达后，开始进入服务通道，如果安检口都忙碌，旅客在服务通道排队等待；反之，旅客直接进入服务口开始接受安检服务。所有旅客在接受完安检服务后离去。基于排队论知识，利用plant-Simulation软件建立不同时段下相应开放通道后的单站排队服务系统仿真模型，其中建模过程中包括基础参数模块、随机数生成模块、动态控制模块、结果输出及评价指标模块这4个模块，如表3所示。建立的单站排队服务系统仿真模型如图3所示。

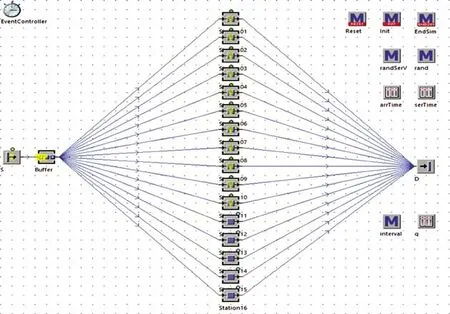
图3 单站排队服务系统仿真模型

表3 仿真平台搭建各模块参数设置

4.2 仿真真实性检验

在仿真平台，根据拟合分布产生各个随机到达旅客和实际各个时段平均开放通道数作为仿真输入进行1 000次仿真，仿真完成后与实际情况进行对比，各项评价指标如下。

（1）各个时间段的过检旅客数如表4所示（节选）。

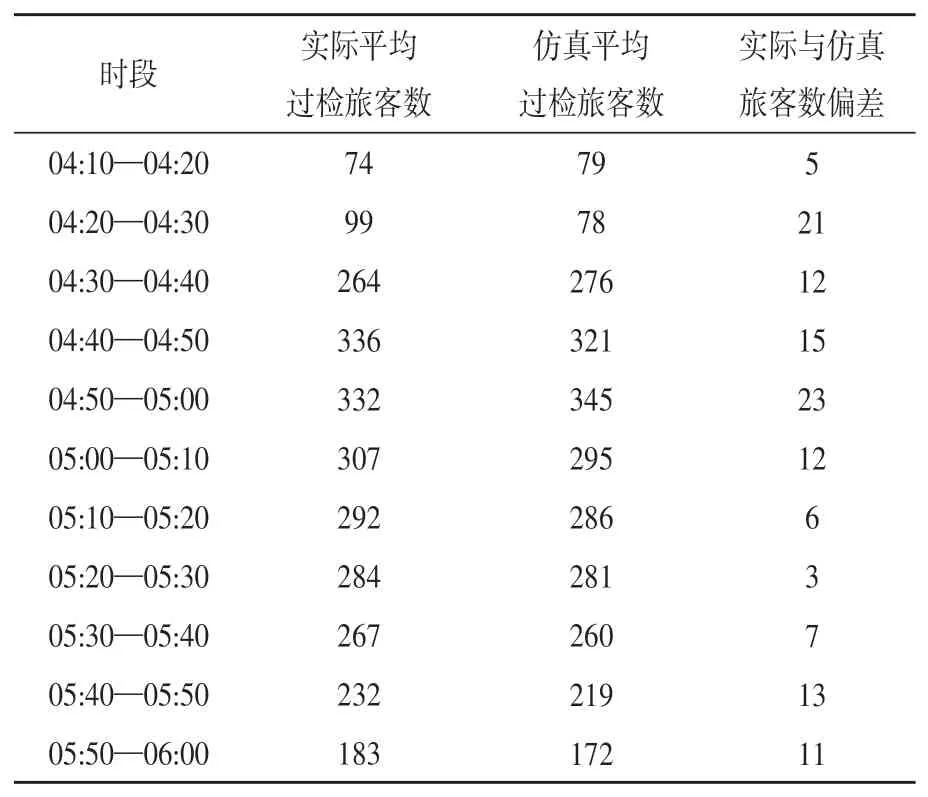
表4 04:00—06:00各时段过检旅客数

（2）每天平均总到达旅客数与平均总过检旅客数。实际情况下，每天平均到达的总旅客是11 825人，平均总过检人数是11 714人，仿真实验下每天平均到达总旅客数为11 604人，总过检旅客数为11 518人，人数偏差在可接受范围内。

4.3 仿真模型

（1）仿真建模。通过随机数生成独立的旅客到达时间以及对应的服务时间。当旅客到达后，在Buffer等待，若有服务台空闲时，则进入服务台接受服务。旅客在等待过成中，采用先到先服务的排队规则，当所有开放服务站都有旅客在接受安检服务时，后续到达旅客选择在等待区域等待。当旅客接受完服务后，旅客离开服务系统。

（2）实验假设。该服务系统每天运作111时段（即18.5 h）。

（3）实验设计。仿真独立运行10次，每次仿真运行长度为1 000天（每天18.5 h）。

（4）实验环境。使用计算机运行Plant-Simulation软件得出结果（即历史计划）。

4.4 仿真优化

提出在数学模型优化结果（表2）的基础上进一步进行仿真优化，实现资源的更合理有效利用，同时降低资源不足的风险。其中为了避免偶然性，采用3西格玛原则，剔除各个时段仿真验证结果下前5%的最大值，取剩下95%数据的极大值作为仿真优化实验的初始值，将仿真优化后的结果作为最终计划配置班组数。

仿真优化的主要思路是基于数学优化结果得出的初始值进行逐段顺序优化，即随每天时间变迁对每个时段进行基于时段初始值下的配置班组调参实验，当每个时段下的仿真效果无超出风险，同时又使资源利用率较大时可视为较优解（即仿真优化）。

5 结论分析

根据当前机场历史计划配置班组和数学模型结果与仿真优化结果对比，部分时段下的结果对比如图4~8和表5所示。分析可得以下结论。

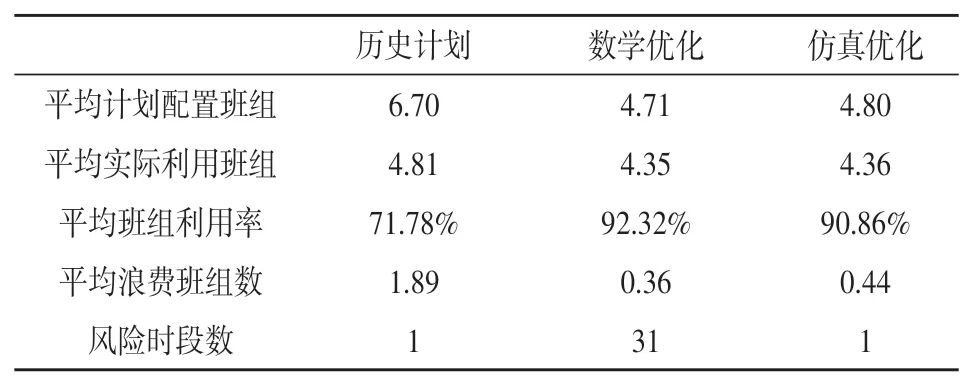
表5 各计划配置方案指标评价对比

图4 各时段计划配置方案班组数对比

（1）历史计划配置方案浪费班组数最高，每个时段平均浪费1.89个班组，几乎无超出风险。

图5 各时段计划配置方案平均等待时间对比

图6 各时段计划配置方案平均等待队长对比

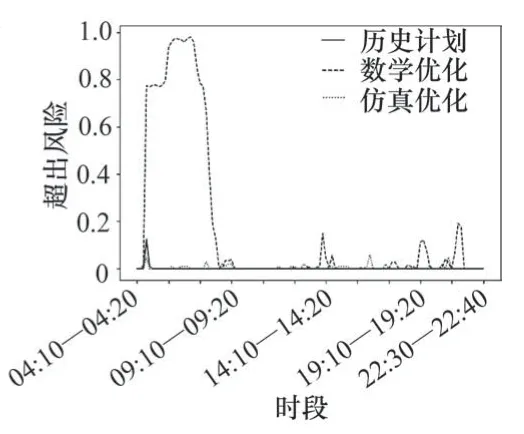
图7 各时段计划配置方案超出风险对比

图8 各时段计划配置方案浪费班组数对比

（2）数学优化结果较历史配置方案平均每个时段节省1.9个班组，班组利用率提高到了92.32%，在部分时段下有极大风险概率旅客等待时间过长。

（3）仿真优化结果较历史配置方案，旅客平均等待时间有20~120 s的小幅增长，但大部分时段在合理范围内；平均每个时段节省了1.9个班组，班组利用率提高到90.86%，几乎不存在超出风险。

（4）在旅客可接受范围内，适当增加旅客等待时长，通过仿真优化配置方案，可以在进行风险管控的同时节约人力成本。以广州市2019年最低月薪2 200元和每天8小时制，每年可以节省19个人员，为企业节省69万元的人力成本。

6 结束语

随着航空出行的普及，机场的安检旅检工作变得举足轻重，传统的安检旅检通道安排已经无法在当前的航空业竞争中获取优势。针对上述的问题，本次机场安检通道的动态优化配置方法，通过对安检现场的调研以及对该业务室的服务准则作为切入点，对机场安检部门当前的配置方案进行仿真实验。根据调研数据的分析结果，在仿真服务系统上验证服务时间和到达间隔时间随机分布，以及GI/G/m单站排队服务系统近似公式的精确性。最后根据安检通道数学模型优化结果和实际开放通道数以及仿真优化的对比结果，得到一个不同时段的通道配置方案。本次研究取得了以下成效。

（1）该方法生成了一个动态灵活的、与旅客贴合度更高的通道配置方法，实现了通道数的优化，使得通道与人力资源都得到了有效的配置，充分地提高了资源利用率，降低了安检服务工作成本，令安检服务效率显著提升。

（2）在本方法的作用下，能有效地减少旅客的排队时间，提高旅客对服务的满意度，从而增强了机场的行业竞争力。

（3）本方法不仅可以应用于机场安检部实现安检通道的动态优化配置，同样可以应用于机场其他地勤服务部门实现动态过程下的资源优化配置。亦可应用于国内各大机场以及在其他进行动态资源优化服务的行业进行推广。