附加水平支撑桁架对爬架的力学响应分析

王银刚，欧阳芳，聂 琼，柯贤孝

(1. 湖北第二师范学院 BIM技术应用工程中心，武汉 430205；2. 湖北省BIM智慧建造国际科技合作基地，武汉 430205；3.中国水利水电第七工程局有限公司，成都 610213)

1 引言

附着升降式脚手架(亦称爬架)是现代超高层建筑施工中不可或缺的重要施工工具。爬架主要有传统钢管爬架、半钢式爬架、全钢式爬架三种，其中全钢式爬架架体全部使用型钢、钢板等钢材组合加工而成，具有较高的安全性、防火性、适用性和智能化，是目前超高层建筑施工首选的爬架类型。近10多年来，工程师和学者对爬架的计算方法和理论做了深入研究，但大都局限于传统钢管爬架，[1]-[4]对全钢式爬架的研究较少。

对于全钢式爬架，通常需在架体底部增设水平支撑桁架来对其加固，以增强爬架体系的整体性，提高其刚度。有研究[5]表明，水平支撑桁架的设置显著降低了架体的应力和位移，是一种可靠、经济的加固方式。然而，水平支撑桁架根据其在架体底部的位置的不同有多种布置方式，各种布置方式对架体受力的影响各有差异，因而有必要研究各种布置方式下架体的力学响应，优选最佳的布置方式；再者，架体增设水平支撑桁架后，增加了其竖向刚度，在导轨不同爬升工况下可能会产生支座脱空，从而引起架体内力的非线性变化。所以，需进一步研究水平支撑桁架对爬架受力的影响规律，为此类爬架的设计提供理论支撑。

2 爬架有限元计算模型

2.1 几何尺寸

选用某型全钢爬架，取3榀作为研究对象，爬架高度为 13.5m，步高1.9m，共7步，覆盖4.5个楼层，架体宽度0.6m，支承跨度5m。水平支撑桁架设置于架体底部两层，桁高0.6m，水平支撑桁架与架体竖杆之间采用螺栓连接。

2.2 材料

各构件均采用Q235钢材加工而成, 弹性模量取206GPa, 泊松比取0.3,钢材密度7850kg/m3。

2.3 截面特性

梁单元截面特性根据实际几何尺寸由软件自动计算，本例爬架杆件的具体尺寸如下表：

表1 截面特性表Table 1 Section properties table

2.4 有限元模型

采用Midas/Civil有限元软件进行空间分析，爬架杆件采用梁单元。架体及水平支撑桁架的有限元模型分别见图1和图2。计算时，根据水平支撑桁架在架体中的位置激活或钝化相应的桁架单元(图3)。水平支撑桁架与架体竖杆之间采用铰接来模拟螺栓连接。

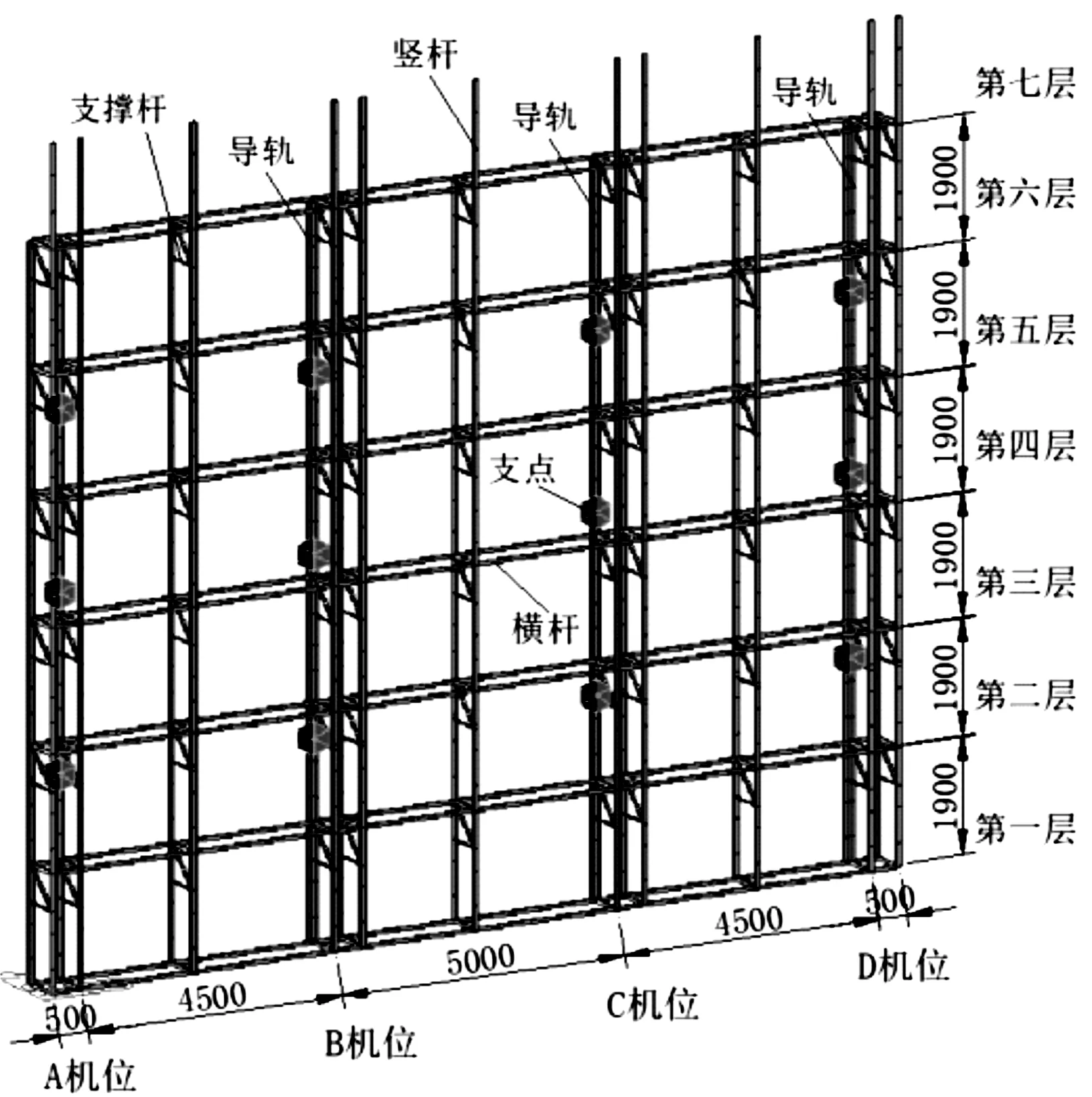
图1 架体有限元模型

图2 水平支撑桁架模型

图3 增加水平支撑桁架后的爬架模型

2.5 荷载取值

施工活载按《建筑施工工具式脚手架安全技术规范》[6]中的规定取值，见表2所示。

表2 施工活载取值

2.6 边界条件

爬架在竖向设三道支撑，支座对爬架导轨在水平方向有X和Y方向的约束，而在竖直方向仅有向下的约束，因此附墙支座在竖向按单向支座模拟。

3 附加水平桁架的布置位置对爬架受力的影响

附加水平支撑桁架设置于架体的竖向平面内，常置于架体底部一、二层。为方便说明，对水平支撑桁架在架体中的位置进行编号，架体第一层内、外侧位置分别为1和2，架体第二层内、外侧位置分别为3和4。根据水平支撑桁架在架体上的位置，有以下六种布置方式(图4)，分别为：

图4 水平支撑桁架布置类型

(1)“12”型：均置于架体第一层；

(2)“13”型：分别置于架体第一层内侧和第二层内侧；

(3)“14”型：分别置于架体第一层内侧和第二层外侧；

(4)“23”型：分别置于架体第一层外侧和第二层内侧；

(5)“24”型：分别置于架体第一层外侧和第二层内侧；

(6)“34”型：均置于架体第二层。

3.1 使用工况

在同一架体模型中，分别按照上述六种不同的水平支撑桁架布置方式进行计算，结果见表3。从表中可知，设置水平支撑桁架后，架体杆件的应力和竖向变形有明显改善。以水平支撑桁架按“24”型布置为例，比起不设水平支撑桁架，横杆应力降低了31.1%，竖杆应力降低了12.6%，爬架的最大竖向位移降低了60.3%。

表3 爬架在不同水平支撑桁架下的计算结果

在六种不同的桁架布置方式中，水平支撑桁架按“13”和“24”型布置(两片桁架在同一竖平面内)时，架体的应力最大，而水平桁架的应力最小，爬架具有较大的竖向位移，由胡克定律可得出，此种布置方式下爬架的竖向刚度最小；其余几种水平支撑桁架的布置方式对爬架的受力影响相当。

进一步对爬架的竖向位移进行分析。如图5所示，爬架横杆在施工活载和竖杆竖向位移的带动下，产生了较大的竖向挠度，规范中对爬架受弯构件的挠度限值为：

图5 爬架竖向位移图

[f]=min(L/150,10)= 10mm

上式中，L为受弯杆件跨度，此处为2500mm。

可见，对于本例，不设水平支撑桁架时，爬架横杆的竖向挠度已超过了规定限值。按前述六种布置方式设置水平支撑桁架后，横杆的竖向位移由12.1mm最少降低到4.8mm，降低了60%以上。可见，水平支撑桁架是保证爬架安全性的有效措施之一，爬架体系设计时，应重视水平支撑桁架的作用。

尽管增设水平支撑桁架后，架体的竖向刚度增大，对爬架结构是有利的。但是，当支座产生强迫位移时，较大的竖向刚度使得在架体内产生的内力也越大。爬架在升降阶段，相邻导轨极易由于升降电机转速不同步或电路故障而发生不同步运动，[7]从而形成支座处的强迫位移差，因此有必要研究爬升阶段，水平支撑桁架对架体受力的影响。

3.2 爬升工况

爬架爬升过程可由图6来说明。准备提升前，先安装支座4，再拆除支座1。整个爬升过程中，架体与附墙支座的相对位置处于变化中，支承位置的改变将引起结构受力的改变。已有文献[7]-[9]在研究爬架爬升工况的安全性时，大都聚焦在导轨不同步爬升下的架体受力，但未关注爬升过程中附墙支座与架体相对位置的改变引起的架体受力改变。本次研究将对比爬架在爬升初态和爬升终态两个瞬态下，不同桁架布置方式对爬架受力的影响规律，以此找出水平支撑桁架的推荐布置形式。

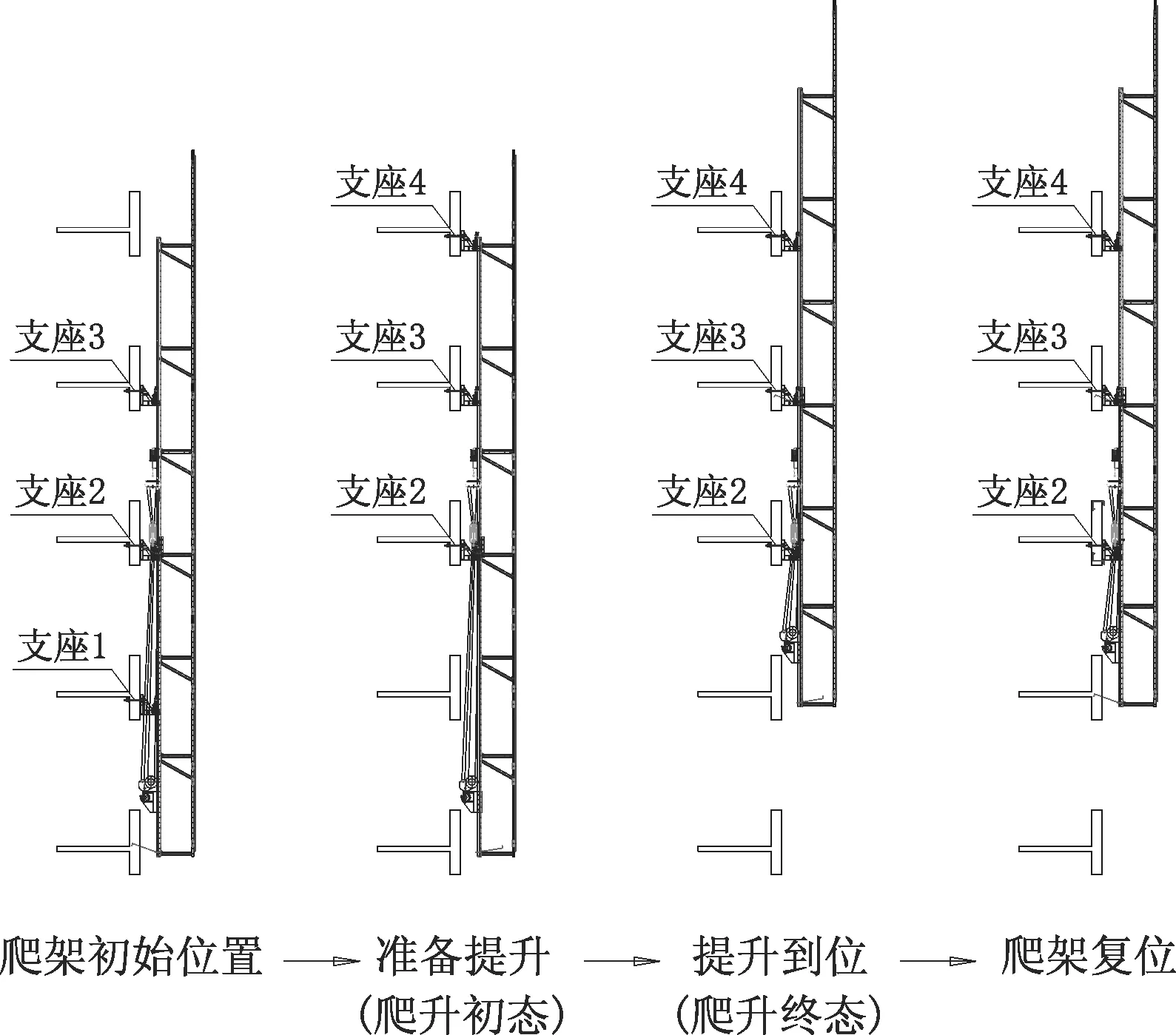
图6 爬架爬升过程

规范[6]规定，爬架爬升过程中，导轨不同步运动位移差Δs不超过30mm。现研究Δs在30mm范围内时，爬架爬升初态和终态时架体及水平支撑桁架的应力，荷载组合考虑表2中的施工活载。

需要注意，由于爬架爬升过程中，附墙支座为单向支座(支座仅能承受压力)，当Δs较大时可能发生支座脱空现象，从而引起架体内力的重分布，因此爬架导轨不同步爬升的过程可能是一个非线性过程，分析时应找出各支座脱空的临界位移值。对于多跨爬架，由结构力学知识知，在各跨跨度相同时，支座产生隔跨位移差时，结构的受力状态最不利。本例中，由于计算模型具备对称的特点，可对A、C支座施加强迫位移来进行研究，此时B、D支座可能会发生支座脱空。注意到当D支点脱空时，爬架为悬臂状态，D节点位移大于B节点，亦即D支座脱空应在B支座脱空之后发生。

令s1和s2分别为B支座和D支座脱空时在相应支座节点处的位移。爬架在A、C支座产生隔跨位移差Δs的非线性过程可以图7加以说明如下：

图7 爬架爬升过程的非线性说明

(1)当Δs

(2)当s1≤Δs

(3)当Δs≥s2时，D支座也脱空，爬架荷载仅由A、C支座承担。

s1和s2可以通过未知荷载系数法求得，具体方法为：将支座初始强迫位移设为未知荷载，并给定初值(可为1mm)，求解满足使支座反力为0的荷载系数，将此荷载系数乘以初值即为所求的解。该步骤可通过计算软件实现，本案例s1和s2的求解结果见表4。

表4 s1和s2计算值

将爬架架体(含横杆和竖杆)和水平支撑桁架分别作为研究对象。图8为不同Δs时架体的最大应力变化曲线，从图中可知无论是爬升初态还是终态，无桁架时，由于架体竖向刚度小，架体能较好地适应导轨不同步运动引起的支座强迫位移，架体应力随Δs的增加呈线性变化，即使Δs=30mm时，架体杆件应力也不超过200MPa,架体仍处于良好的工作状态。

图8 导轨不同步爬升下架体应力

设置水平支撑桁架后，架体应力降低明显，架体应力随Δs呈非线性变化，第一个拐点处Δs=s1，此时B支座脱空；第二个拐点处 Δs= s2，此时C支座脱空，随后架体保持此时的应力水平。计算结果显示，Δs=30mm的架体应力比无桁架时几乎降低了一半。

在不同的水平支撑桁架布置形式中，爬升初态(图7(a))时，六种布置情形的应力曲线几乎重合，彼此相差不大；爬升终态时(图7(b))，按“24”型布置时架体应力最大，其余五种布置相差较小。

导轨不同步爬升过程中，水平支撑桁架的应力变化曲线见图9，尽管Δs在10mm左右时，桁架杆件已屈服，但从其变化趋势不难看出，按“24”型和“13”型布置水平支撑桁架，由于其竖向刚度最小，适应支座不同步位移差的能力也越强，在导轨不同步爬升时其应力水平反而较优，其余四种布置型式差别不大。

图9 导轨不同步爬升下水平支撑桁架应力

对爬架爬升工况的计算结果表明，水平支撑桁架设置在同一竖平面内时，爬架竖向刚度相对较低，对导轨不同步运动下的受力有利，但从工程实用性的角度看，水平支撑桁架布置在爬架外侧，有利于施工人员和材料从爬架内侧进入，因此，按“24”型布置优于“13”型布置。

此外，通过比较同一Δs时爬架在爬升初态和终态的应力值可知，爬升初态的杆件应力要大于爬升终态的杆件应力，以无桁架时导轨不同步运动差Δs=30mm为例，架体在爬升初态与爬升终态的应力值之比为191.9/169.6=1.13。因此，进行爬架升降工况的安全性验算时，建议以爬升初态的计算模型为准。

4 爬架设计体系的探讨

前述分析表明，水平支撑桁架对爬架的受力有显著的影响。一方面，水平支撑桁架增大了爬架的竖向刚度，使得使用阶段的竖向变形变小，对结构是有利的；而另一方面，在爬升阶段，当导轨产生不同步运动时，又会在桁架内部产生较大内力，对结构是不利的。

由于现行规范要求爬架导轨不同步运动位移差不超过30mm，因此以爬升阶段导轨不均匀运动位移差Δs≤30mm时，附墙支座是否脱空为判断条件，可将爬架设计体系分为柔性体系和刚性体系。柔性体系下，在Δs=0～30mm区间内，支座反力呈线性变化，爬架杆件应力亦呈现线性特征。刚性体系下，随着Δs逐步变大，附墙支座脱空，引起爬架内力重分布，杆件应力呈现明显的非线性特征。下面，分别以柔性体系和刚性体系对本案例爬架进行重新计算。

4.1 按柔性体系设计案例爬架

从图8可知，不设水平支撑桁架时，架体应力随Δs线性变化，在Δs≤30mm内不会出现支座脱空。因此，可以尝试在不设水平支撑桁架的情况下通过增加水平横杆的刚度，使架体应力降低的同时又不发生支座脱空。

经试算，水平横杆截面厚度由3mm增加到4.8mm后，当Δs=30mm时B支座开始脱空，此时，架体应力降低到175Mpa(表5)，降低了8.8%。验算架体在使用阶段的最大竖向位移为9.4mm，小于规范规定的挠度限值，满足要求。

表5 按柔性体系设计爬架

图10 按柔性体系优化前后对比曲线

4.2 按刚性体系设计案例爬架

按“24”型布置水平支撑桁架。由图8、图9可知，架体应力满足要求，而水平支撑架应力超标，因此可通过增加桁架杆件的截面尺寸或增加桁架高度来降低桁架杆件的应力，表6为增加桁架截面的计算结果。

表6 按刚性体系设计爬架

5 结论

(1)在爬架底部增设水平支撑桁架可以改善架体结构的受力，减少架体杆件变形，是一种可靠的爬架加固方法。增设水平支撑桁架后，架体竖向刚度增大，应注重对导轨不同步爬升工况的验算。

(2)水平支撑桁架在架体底部两层的不同布置方式中，采用交叉布置方式(即两片桁架分别布置于爬架内侧和外侧)架体应力和变形最小；采用同侧布置方式，可使不同步爬升工况下桁架的应力最小。结合对施工方便性的考虑，推荐水平支撑桁架按“24”型布置(即两片桁架分别布置在爬架底部一、二层的外侧)。

图11 按刚性体系优化前后对比曲线

(3)对爬升工况下爬架在爬升初态和终态两个瞬态的计算表明，爬架在爬升初态的应力大于爬升终态的应力，建议进行爬升工况验算时，以爬升初态的计算模型进行计算。

(4)进行导轨不同步爬升工况验算时，应判断不均匀运动位移差Δs在30mm范围内是否产生支座脱空，若有，则应考虑由支座脱空引起的内力重分布，从而引起的爬架应力的非线性变化。

(5)以爬升阶段导轨不均匀运动位移差Δs≤30mm时，附墙支座是否脱空为判断条件，提出将爬架设计体系分为柔性体系和刚性体系，支座无脱空则为柔性体系，否则为刚性体系。本文对案例爬架分别用这两种体系进行了重新设计，可为此类爬架的设计提供参考。