闭区间上连续函数有界性的教学研究与应用*
毛安民
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
在我国的高等教育课程体系中,数学专业课程《数学分析》是一门非常重要的专业基础课和入门课程; 对连续函数的性质的教学研究一直是个很重要的研究课题,究其原因在于该类课题研究涉及到《数学分析》最基本、最核心的知识点,而且此类研究往往会激发很多富有智慧的数学思想,极具启迪意义.闭区间上的连续函数的有界性定理,就是连续函数的非常重要的一条性质,该性质的证明涉及到函数连续性、函数极限、归结原则和反证法等若干重要知识点和证明技巧的运用,故对该性质的证明思路和技巧的掌握,是非常重要的教学目标.
我们列举两个不同的连续函数有界性定理的证明,证明分别来自于华东师范大学数学科学学院编著的数学分析教材[1]、北京大学数学系伍胜健教授编著的数学分析教材[2],后者给出的证明与复旦大学陈纪修等编著的数学分析教材[3]给出的证明如出一辙.上述3种不同的数学分析教材是目前国内诸多高校广为采用的教材,极具代表性.
定理1[1]设函数f∈C[a,b].则f在[a,b]上有界.
证明若不然,不妨假设f在[a,b]上无上界.那么存在xn∈[a,b],使得
f(xn)>n,n=1,2,3,…,
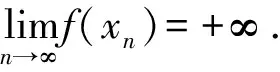
a≤xnk≤b,
利用极限的保不等式性质推得
a≤x0≤b,
故由f在点x0连续,结合归结原则导出
矛盾,故原结论成立.
上述证明所用方法为反证法,结合致密性定理、数列极限保不等式性及归结原则等重要知识点完成了证明.下面给出有界性定理的另一种证明,该证明来自北京大学数学系伍胜健编著的数学分析教材[2].
定理2[2]设函数f∈C[a,b].则f在[a,b]上有界.
证明倘若f在[a,b]上无界,则将[a,b]等分成两个区间,f必在其中一个区间上无界,取定这样的一个区间并将其设为[a1,b1].同理,再将[a1,b1]二等分,f必在其中一个子区间上无界,取定这样的一个区间将其记为[a2,b2].如此进行下去,我们得到一个闭区间列{[an,bn]},满足
(1)[an,bn]⊇[an+1,bn+1];
(3)f在每一个[an,bn]上都无界.
于是,由闭区间套定理知,存在唯一的ξ∈[an,bn],n=1,2,3,….再由f∈C[a,b]和ξ∈[a,b]知,存在δ>0使得f在U(ξ,δ)∩[a,b]有界.而条件(2)又蕴含着,当n充分大时,有[an,bn]⊂U(ξ,δ),从而f在[an,bn] 上有界.这与条件(3)矛盾,故原结论成立.
复旦大学陈纪修等人编著的数学分析教材[3]中对有界性定理的证明和上述证明如出一辙,也是反证法,核心思想是利用闭区间套定理获得矛盾.
受以上工作的启发,本文我们将给出一个新的证明思路,该证明思路的核心是确界原理的应用,当然也涉及到确界的一些重要性质的运用.作为进一步的研究,我们将此新的证明思路应用于研究连续函数的其他性质,诸如相邻的两个最值点区间的确定、连续函数介值定理.
1 研究成果及应用举例
下面给出本文的研究成果,一个完全不同于上述教材的有界性定理的证明.
定理3 设函数f∈C[a,b].则f在[a,b]上有界.
证明由于f∈C[a,b],故根据函数在一点处连续的局部有界性性质知,存在δ>0使得f在[a,a+δ]⊂[a,b)上有界.令
E={x∈[a,b]|f在区间[a,x]上有界},
知a+δ∈E,故E≠Ø.由确界原理知集合E有上确界,设supE=β,则a<β≤b.下证β∈E.由于f在β点连续,故存在δ′>0使得f在[β-δ′,β]有界.存在γ∈[β-δ′,β]使得f(x)在[a,γ]上有界,从而f(x)在[a,β]上有界,故β∈E.
下证β=b.若不然,假设β
从局部出发渐变到整体,将局部性质推演为整体性质,是上述证明的出发点和入手点.利用这一思想,我们下面研究连续函数的相邻的两个最值点构成的区间问题和连续函数的介值定理的证明.
例1 设函数f∈C[a,b],m,M分别是f的最小值和最大值.则存在α,β∈,满足
(1)[α,β]⊂[a,b];
(2)α,β或是最大值点和最小值点,或是最小值点和最大值点;
(3)任意x∈(α,β),m 证明由f∈C[a,b]知,f存在最大值M和最小值m,及最大值点x1和最小值点x2,f(x1)=M,f(x2)=m.不妨设x1 E1={x∈[a,b]|f(x)=m,x1 知x2∈E1,E1⊂[a,b].故E1是非空有界集合.由确界原理知,E1有下确界,令β=infE1,从而存在数列{xn′}⊂E1,xn′→β,n→∞.由f的连续性和归结原理得 f(xn′)→f(β),n→∞, 又{xn′}⊂E1,得f(xn′)=m, 故f(β)=m.根据x1≤β≤x2和f(x1)=M,知x1<β,而且(x1,β) 里面再无其他最小值点. 下面寻找β左边的相距最近的最大值点α.令 E2={x∈[a,b]|f(x)=M,x<β}, 知x1∈E2,E2⊂[a,b].故E2是非空有界集合.由确界原理知,E2有上确界,令α=supE2,从而存在数列{xn″}⊂E2,xn″→α,n→∞.由f的连续性和归结原理得 f(xn″)→f(α),n→∞, 又{xn″}⊂E2,得f(xn″)=M, 故f(α)=M.根据x1≤α≤β和f(β)=m,知α<β,而且(α,β) 里面再无其他最大值点.又 由(α,β)⊂(x1,β),可知(α,β)里面也无最小值点. 综上可知,(α,β)里面没有最大值点和最小值点,故即为所求. 采用同样的思想,下面来证明连续函数的介值定理. 例2 设函数f∈C[a,b],f(a)≠f(b).若μ为介于f(a),f(b)之间的任何实数(f(a)<μ 证明依题意,不妨设f(a) 下面证明x0即为所求的点.首先,根据supE=x0知,存在数列{xn}⊂E,使得xn→x0(n→∞).根据函数f的连续性,得f(xn)→f(x0)(n→∞).由f(xn)<μ,利用数列极限的保不等式性质知,f(x0)≤μ.其次,接下来用反证法证明f(x0)=μ.假设f(x0)<μ, 则由函数极限的保号性性质知,存在x′∈(x0,b),f(x′)<μ,则x′∈E且x′≤supE=x0,矛盾! 故反证假设不成立,知f(x0)=μ.

