对数螺旋锥齿轮参数化建模及其动态加工仿真研究
王忠利 李 鹏
(1、郑州科技学院 电气工程学院,河南 郑州450064 2、河南工程学院 机械工程学院,河南 郑州 451191)
对数螺旋锥齿轮广泛应用于汽车、直升飞机、工程机械、机床、船舶等机械产品中。在机械传动性能日趋要求提高以及常规螺旋锥齿轮制造技术几乎被国外垄断的背景下,一种啮合与传动性能更优的新型的对数螺旋锥齿轮技术研究就显得更加亟需迫切。与常用的螺旋锥齿轮相比,对数螺旋锥齿轮具有螺旋角相等、传动性能好等诸多优点,且齿线上每一个点的螺旋角均相同,即在齿线的沿线方向上螺旋角没有发生变化,因此当齿高线随时啮合时,啮合力的变化最小,保持了螺旋锥齿轮的平稳传动。齿面接触状态越来越好,工作过程非常稳定可靠而无任何噪声。
本文以新型对数螺旋锥齿轮的参数建模、动态仿真与加工等关键技术为研究对象,从计算机辅助工程/分析(CAE)的角度,就对数螺旋锥齿轮的三维参数化建模、自由模态分析、啮合仿真、接触数值分析及五轴联动数控加工实物等个方面进行深入的研究和分析,然后再和普通螺旋锥齿轮各方面性能进行对比,总之,该新型对数螺旋锥齿轮的啮合和传动特点优于普通对数螺旋锥齿轮,其具有较高的理论价值和现实意义。
1 对数螺旋锥齿轮的三维参数化建模
本文基于Boolean 求差运算的三维参数化建模。提出了基于Boolean 减法的建模方法,以基本参数有齿数是37:9,模数是45mm,压力角是200,螺旋角是350的对数螺旋锥齿轮为例,并对其采取高精细化建模。基于CONTURA G3 3D 坐标测量仪并采用实验数据分析和理论研究二者相结合的方法,进行分组测量和比较了大小齿轮的轮廓误差和加工误差,大齿轮大端齿顶圆直径的实验测量与理论计算的误差为0.0033mm,小齿轮计算误差为0.0033mm。
主要选用UG/OPEN GRIP 确定为二次开发使用工具,通过优化设计使得参数建模的界面非常清晰且准确,从而可以对数螺旋锥齿轮实施更好的3D 参数建模。
螺旋锥齿轮主要由五个锥面和四个角度组成,如图1 所示。为了使三维模型达到最佳效果,方便对数螺旋锥齿轮仿真分析研究,根据对数螺旋锥齿轮的形成机理进行较准确的建模。
利用面锥体与齿槽体Boolean 减法的数据计算方法,对对等角螺线锥齿轮执行三维精细化和最优化建模。基于大端和小端渐开线齿槽截面线并沿对数螺旋锥齿轮的齿线作为扫掠路径形成的称为齿槽体三维造型方法,需要对单齿槽体进行排列后才能得到对数螺旋锥齿轮的所有齿槽体,排列单齿槽体后,得到对数螺线锥齿轮的所有齿槽体。使用面锥体和所有齿槽体进行Boolean 减法数据的计算方法,建立对数螺线锥齿轮模型。

图2 建模流程图
对数螺旋锥齿轮装配体建模:
对建模所得到的模型进行装配,装配时采用约束的方式进行定位。按照以下三个约束条件进行装配:(1)主动小齿轮和从动大齿轮的轴线相互垂直,即轴交角为90°;(2)主动小齿轮和从动大齿轮的节锥顶点重合;(3)主动小齿轮和从动大齿轮的齿面在啮合点处相互接触。装配后的模型如图3 所示。
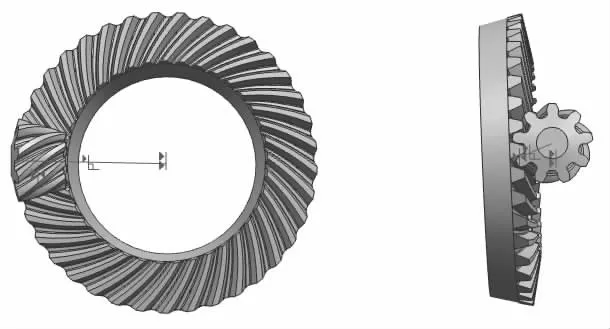
图3 对数螺旋锥齿轮装配模型
2 啮合角速度及切向接触力仿真分析
根据赫兹接触的切向接触力与啮合角速度仿真过程。借助赫兹接触理论研究方法,我们建立了锥齿轮啮合角速度与切向接触力的仿真模型。揭示了对数螺线锥齿轮的切向接触力与啮合角速度的基本工作过程。对传统齿锥齿轮与角速度齿轮啮合时的切向接触力和切向接触力的工作状态和性能进行了仿真分析,并构建了均值-极差控制图对仿真数据进行客观分析处理。实验数据表明,对数螺旋锥齿轮的啮合和传动的稳定特性好于普通螺旋锥齿轮的性能。
根据仿真实验操作步骤,动力学仿真模型基于UG Motion 环境中建构。由于冲击载荷会随时发生变化,从而引起旋转角速度的突变,所以对数螺旋锥齿轮的小齿轮的角速度一定要使用阶跃函数。小齿轮的角速度为7702.87°/s,从动大齿轮的扭矩为1964.99N·m。仿真时间为1s,仿真时长为500 步。在相同的初始条件下模拟了啮合角速度和切向接触力仿真分析。
图4 显示了随着时间的变化,常用的螺旋锥齿轮和对数螺旋锥齿轮小齿轮的旋转角速度的曲线图。小齿轮采用阶跃函数,小齿轮的角速度在0.2 秒前逐渐线性增加,但是之后小齿轮的角速度比较稳定,为7702.87°/s。

图4 小齿轮输入角速度曲线

图5 仿真流程图
对数螺旋锥齿轮大齿轮输出角速度仿真结果如图6 所示,在0~0.2 秒,其角速度与时间接近线性的增长,0.2 秒后趋于稳定,但仍存在上下波动,导出0.2 秒后的仿真数据,经计算得大齿轮角速度的仿真平均值为1873.77°/s。在UG 环境中,再克隆一个新仿真,创建理想齿轮副,设置其齿数比为9:37,用理想齿轮副进行仿真,得出理论上大齿轮的角速度随时间的变化曲线如图7 所示,0.2 秒后,大齿轮的角速度为1873.703°/s。基于大齿轮啮合角速度模拟的情况下,其在0.2 秒后变得稳定,图8为随着时间的变化,幅值相应变化的散点图。图8(a)为常规螺旋锥齿轮,图8(b)为对数螺旋锥齿轮。从本图中可以观察出,在相同参数下,与常规螺旋锥齿轮相比,对数螺旋锥齿轮传动的从动大齿轮的角速度的变化范围小,传动性能比较稳定。
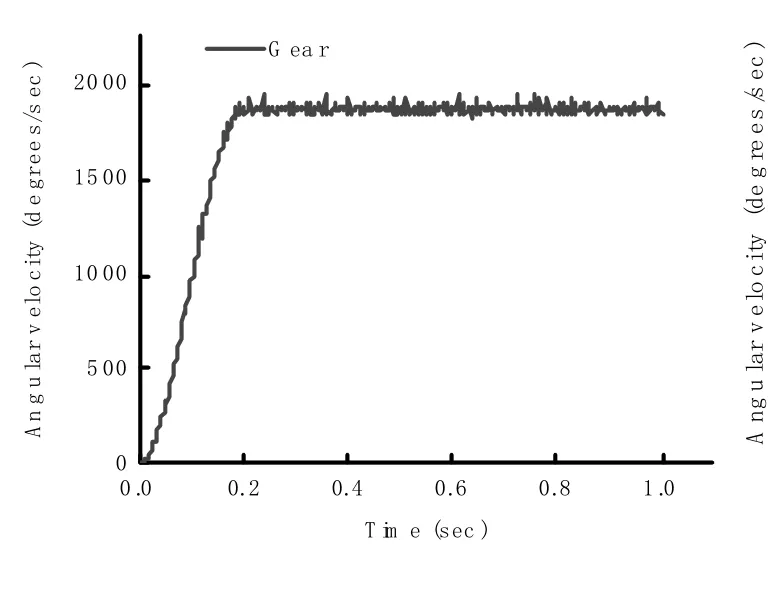
图6 LSBG 大轮仿真角速度曲线

图7 大齿轮理论角速度曲线

图8 啮合角速度与时间的散点图
3 有限元自由模态分析
基于Lanczos 法的自由模态分析与基于PolyMax 法的实验模态验证。首先采用理论研究的方法,基于Lanczos 数值计算方法进行迭代求解计算求特征值和特征向量,得出固有频率和主振型,就对数螺旋锥齿轮的小齿轮、大齿轮及装配体和常规螺旋锥齿轮的大齿轮做有限元自由模态分析。再次,采用实验模态分析验证的方法,借助LMS 模态分析模块,搭建螺旋锥齿轮自由模态分析的实验平台,采用最小二乘复频域的PolyMax 方法提取实验模态参数。实验模态测试的结果与有限元模态分析的结果有较好的一致性。为对数螺旋锥齿轮的瞬态动力学分析、模态叠加法求响应、谱分析、振动控制、故障振动和动力学优化设计等CAE 技术提供依据。
4 螺旋小齿轮加工分析
五轴数控加工技术及铣削参数优化设计研究,通常以实验研究和实验数据分析为主线,在车床C6140A1 上加工对数螺旋锥齿轮工件,然后,依据球头铣刀和对数螺旋锥齿轮的关系,形成车刀车削过程,确定尺寸,编制对数螺旋锥齿轮数控加工与编程的车削路径。设计参数主由主轴转速、进给速度、吃刀量,然后,以最小加工小时数为优化目标函数,对对数螺旋锥齿轮大齿轮数控铣削参数进行优化。最后,在德马吉五轴数控立式加工中心加工出与对数螺旋锥齿轮的大小相符合的齿轮。
图9 显示了待加工的对数螺旋锥小齿轮的尺寸图。其主要采用45 钢为制作材料,加工工艺结构如下:首先,在普通车床上固定切割材料夹的位置,制作出定位基准,然后轴肩安排粗加工,精加工时务必选择特别重要轴肩的安装定位进行。然后以轴颈加工为定位基准制作对数螺旋锥齿轮的齿坯,然后加工所需要的内外螺纹。安排专用机床来加工小齿轮轴花键,此步特别重要,小齿轮对数斜齿面在专用的5 轴立式加工中心加工完成。通常对数螺旋锥齿轮的小齿轮齿面复杂,其加工工艺要求非常高,加工难度非常大。因此,采用专用五轴立式加工中心Demagi DMU 40 Monoblock 来加工实物。

图9 对数螺旋锥齿轮小齿轮主要尺寸图
5 结论
5.1 提出了一种基于布尔减法运算的对数螺旋锥齿轮建模方法,对对数螺旋锥齿轮进行3D 精细化建模。
5.2 构建均值-极差控制图来评估螺旋锥齿轮的传动稳定性。通过比较啮合角速度和切向接触力与构建的均值-极差控制图,对常规螺旋锥齿轮传动和对数螺旋锥齿轮传动的稳定性进行了评价。
5.3 建立了基于最大加工效率的对数螺旋锥齿轮铣削参数优化数学模型。对其大齿轮五轴立式数控加工中心技术参数进行了革新与优化,提高实际应用价值。

