立式管道泵断电过渡过程内流特性分析

张晨滢，裴吉，袁寿其，王文杰*，甘星城，邓起凡，赵建涛，张本营

(1. 江苏大学国家水泵及系统工程技术研究中心，江苏 镇江 212013； 2. 山东双轮股份有限公司，山东 威海 264200)

在实际运行过程中，离心泵的非正常断电过渡过程是一种极为危险的过渡过程，一旦突发断电后，叶轮只受水流影响，此时离心泵内部流态会在短时间内发生显著变化，从而影响泵机组的安全稳定运行.

近年来，水力机械的启动和停机等过渡过程的水力特性研究引起了广泛关注[1-3]，国内外学者在离心泵[4-6]、轴流泵[7]、混流泵[8-9]等不同类型的水力机械[10-12]方面展开了一系列有价值的工作.KAN等[12]对轴流泵失控引起的失控工况进行了研究,发现在达到最大失控速度前，扬程、转速和流量会显著下降.李伟等[7]研究了启动过程中叶轮内的能量分布及其对混流泵瞬态特性的影响，发现随着叶轮转速的增加，正负涡流交替出现. LI等[11]探究了泵模式下水泵水轮机关机过程中导叶关闭时的流动机理，发现在导叶关闭结束时流态极不稳定，产生大量旋涡并逐渐扩散到所有通道.LI等[2]采用计算流体力学方法研究了离心泵在快速启动过程中的三维非定常不可压缩黏性流动，对比模拟结果和试验结果证明了三维数值模拟过渡过程的可行性.

目前，在对水力机械启停过渡过程研究中，以离心泵为研究对象的文献资料较多.但管道泵与常规离心泵有所不同，因其特殊的安装需求，其进水管设计为特殊的肘型弯管结构，因此其入流方式为非均匀入流.该结构在断电停机过渡过程中比常规离心泵更容易引起流场的畸变流，导致管道泵内部出现不稳定流动，影响其安全稳定运行.因此，立式管道泵断电停机过程中的瞬态内流特性研究尚需深入.文中以立式管道泵为研究对象对断电过渡过程进行研究.采用Fortran语言与CFD结合，预测断电过渡过程中转速的变化.探究管道泵断电过渡过程中，内部流动特性及转速、流量、扭矩动态变化规律，为改善管道泵的设计性能和实际运行性能提供理论依据.

1 数值模拟方法与计算模型

1.1 控制方程

管道泵断电过渡过程内部流场流态可视为复杂的三维黏性非定常不可压缩的湍流湍动，其内部流动规律可由质量守恒定律和动量守恒定律推导得出，其控制方程如下.

连续性方程

(1)

动量方程

(2)

式中：ρ为流体密度，kg/m3；t为时间，s；u为流体速度矢量，m/s；∇为散度；τ为应力张量，N/m3；p为压力，Pa；Sm为源项，N/m3.

1.2 变转速方法

在管道泵突发断电的过程中，其外负载迅速减小至0，有效负载力矩为0.因此其运动方程满足角动量微分方程

(3)

式中：Mt为主动力矩,N·m；J为机组的总惯性矩，kg·m2；ω为旋转角速度，rad/s.

对式(3)进行差分离散，可获得差分方程

(4)

式中：Mi为主动力矩，N·m；Δt为计算时间步，s.

基于式(4)，使用Fortran语言对CFX进行二次开发，根据上一步的流动情况，精确计算下一步转速.具体的算法如下.

具体过程如下： ① 对管道泵正常工况运行情况进行非定常计算，得到稳态工况下的初始值；② 在CFX Solver中，得到扭矩、转速等节点信息；③ 利用自编Fortran程序，调用上一步的扭矩和转速值，根据角动量微分方程计算新的转速；④ 把新的转速导入CFX Solver 进行下一步计算；⑤ 重复以上步骤，直到转速达到飞逸转速，即扭矩动态稳定在0.图1为断电过渡过程算法历程图.

图1 断电过渡过程算法历程图

1.3 计算模型与边界条件

以某立式管道泵为研究对象，水体模型如图2所示.文中研究的立式管道泵主要设计参数中，转动惯量J=0.032 kg·m2;设计流量Qd=50 m2/h;设计扬程Hd=20 m;转速n=2 910 r/min;比转数ns=132.36;叶轮进口直径Din=72 mm;叶轮出口直径Dout=136 mm;叶片数Z=6;进口管直径DPi=80 mm.

图2 立式管道泵计算域图

采用ICEM-CFD对各个过流部件进行结构网格划分，不同计算域之间采用交界面的形式.综合考虑计算精度和计算成本，选取全流域内网格总数164万，其中，进口管、蜗壳、叶轮和出口管的网格数分别是670 298，537 389，239 591，193 350.

1.4 试验验证

为保证计算结果的可靠性，文中将计算结果与试验结果进行了对比.验证试验在江苏大学国家水泵及系统工程技术研究中心的开式试验台上完成，如图3所示.试验台精度达到国家B级标准，其进出口压力传感器不确定度小于±0.1%，流量计误差等级为0.1%，试验结果的综合误差小于2%.对相应工况进行数值模拟，并取最后3圈非定常计算结果的平均值绘制外特性曲线.对比试验结果与计算结果，如图4所示.由图可见，在本研究中涉及的正向流量范围内，扬程最大误差为2.13%，效率最大误差为1.89%，满足后续的研究精度要求.

图3 立式管道泵试验台

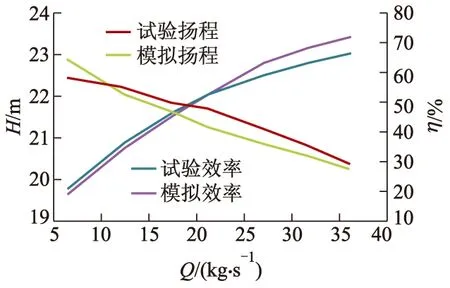
图4 试验结果与计算结果对比

采用商业软件CFD模拟立式管道泵断电过渡过程.在计算中采用SST湍流模型.进出口条件均采用压力边界条件，进口给定总压为101.325 kPa，相对参考压力设置为0、出口给定正常运行情况下非定常计算得到的总压为291 701 Pa.

在求解控制方面，以正常工况下非定常计算结果作为初始条件，之后进行断电过渡过程的模拟.在数值计算中，时间步长△t设置为1.7×10-4，所有参数收敛标准均为收敛精度10-4，总历时3.753 8 s.

2 断电过渡过程结果分析

2.1 外特性参数分析

为了分析各个参数在管道泵断电过渡过程中的变化，将主要参数的动态值与初始值进行了比较.采用的管道泵数值模拟计算初始流量Q0=13.5 kg/s,初始转速n0=2 910 r/min,初始扭矩M0=11.3 N·m.

管道泵断电过渡过程的转速n、流量Q、扭矩M的变化规律如图5所示，图中T1为管道泵突发断电的起始阶段，T2为反向流量和正向流量相等即Q=0的工况点，T3为反向流量超过正向流量，转速仍为正向转速的工况点；T4为转速n=0的临界工况点；T5为倒转倒流阶段的代表工况点；T6为达到飞逸转速时的代表工况点.由图可知，转速n先减小至0，后逐渐增大至飞逸转速保持不变；流量Q先减小后增大，当反向流量增大至Q=-20.809 kg/s后，反向流量逐渐减小，最后稳定在飞逸流量Q=-14.886 kg/s;扭矩M的变化规律呈现出与流量Q一致的现象.整个断电过渡过程分为4个阶段：正转正流阶段、正转倒流阶段、倒转倒流阶段、飞逸转速阶段.

图5 宏观参数变化图

正转正流阶段(t=0～0.242 4 s)，管道泵处于正常水泵工况.突发断电后，水流失去外负载动力，流量和转速均开始下降.转速从2 910 r/min下降至2 368 r/min，与初始速度相比下降了18.63%.流量从初始流量Q=13.530 kg/s迅速减小至0，该阶段流量和转速呈正相关关系，扭矩达到谷底.

正转倒流阶段(t=0.242 4～1.170 4 s)，管道泵进入制动工况.由于压差作用，流量从正向流量转变为反向流量，转速由于惯性作用仍为正向转速，受到反向流量的冲击，转速迅速减小，且随着反向流量的逐渐增大，转速减小的速率不断增加.当t=1.170 4 s时，转速n到达零点，Q=-19.182 kg/s,M=13.4 N·m，在正转倒流阶段扭矩M震荡上升.

倒转倒流阶段(t=1.170 4～2.415 3 s)，管道泵进入水轮机工况.转速反向增大，流量继续增加至Q=20.794 kg/s后，由于水流自身惯性驱动的影响，水的进流速度受到一定的影响，出现一段时间的转速上升而流量减小的现象.扭矩M达到峰值14.1 N·m后平顺下降.

飞逸阶段(t=2.415 3～3.753 8 s)，管道泵在进入飞逸转速阶段, 扭矩M从2.00 N·m逐渐震荡减小至0.转速达到飞逸转速3 510.61 r/min,为原始转速的1.21倍，流量稳定在15 kg/s，该流量即飞逸流量.

2.2 压力时域图分析

根据上述分析，选取6个具有代表性的时刻作为内流分析的特征时刻，如图5所示.

图6为立式管道泵蜗壳隔舌处的压力脉动时域图.由图可知，在立式管道泵断电过渡过程中，压力脉动幅值波动范围大.过渡过程初始时刻T1时，压力脉动幅值为1.7×105Pa.随后隔舌处的压力脉动减小，T2时刻出现第1个波谷.经历短暂的波动后，压力脉动突然上升，并在制动工况保持相对稳定的波动，压力脉动幅值平均值为2.4×105Pa.直至0.96 s时，压力脉动幅值突然开始降低，在T4时刻出现第2个波谷.接着压力脉动幅值开始直线上升至飞逸临界点并稳定在2.9×105Pa.

图6 隔舌处压力脉动时域图

2.3 进口弯管内流分析

取肘型弯管中心截面，如图7所示.定义Ii(i=0,1,…,5)为弯管外侧，Oi(i=0,1,…,5)为弯管内侧，IiOi(i=0,1,…,3)为第1弯管，IiOi(i=4,5)为第2弯管.

图7 肘型弯管平面图

管道泵断电过渡过程肘型弯管流线如图8所示.T1时刻，管道泵开始经历断电失去外荷载过渡过程.总体上流线平顺光滑，由于其特殊的肘型进口结构，进口管内侧流线较为密集，外侧流线较为稀疏，第1弯管和第2弯管内侧流速较第2弯管外侧流速大.第1弯管I2O2断面外侧位置存在1个小旋涡.

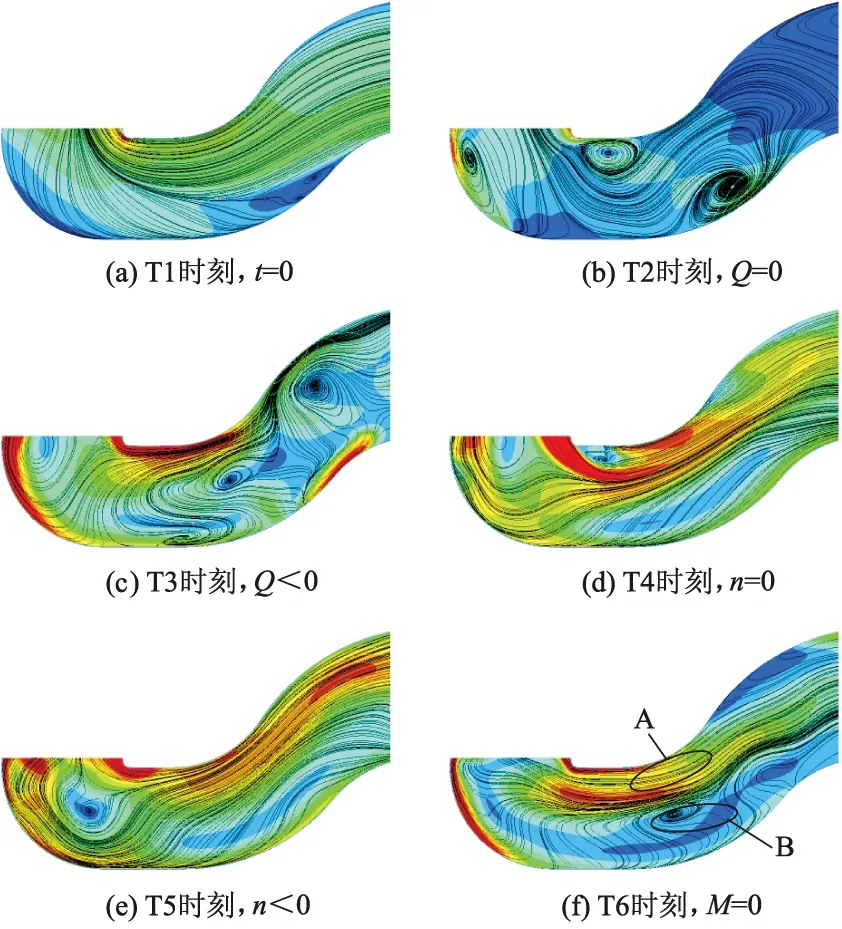
图8 进口肘型弯管截面速度分布特性

T2时刻，流量到达零点，进口流道内的流线与T1时刻相比发生了剧烈变化.断面I2O2外侧,断面I3O3内侧,断面I4O4外侧均出现了流动分离并产生大旋涡，且第1弯管断面I2O2外侧的小旋涡增大.泵工况内部流场复杂多变.

T3时刻，流量为负值，与T2时刻相比流态持续恶化.发现旋涡逐渐向断面I1O1内侧、I2O2断面中间位置和断面I5O5外侧移动，第1弯管断面I2O2外侧的小旋涡逐渐消失.制动工况内部流场同样复杂多变.

T4时刻，转速n开始从正方向转变为负方向，与T3时刻相比，流线逐渐平滑光顺.第1弯管内侧和第2弯管流速较第1弯管外侧流速大.第2弯管进口肘型弯管流道内旋涡消失，第1弯管断面I2O2外侧位置旋涡消失.

T5时刻，转速为负方向，与T4时刻相比流速明显增大，流态略微紊乱.断面I4O4中间位置出现旋涡.水轮机工况内部流态较为整齐.

T6时刻，转速n达到最大转速即飞逸转速，流态较T5时刻复杂.肘型弯管内部流态一分为二，靠近弯管内侧水流A流速较快，流线整齐光顺，另一半水流B垂直于水流A和弯管外侧，由于两股水流出现流动分离，在水流A,B交界面和断面I3O3的交线处出现小旋涡.

2.4 叶轮横截面压力及流线分布

取叶轮中心截面，绘制流线图和压力云图，如图9所示，对断电过渡过程叶轮内流场进行分析.

图9 叶轮压力流线分布特性

T1时刻，管道泵突然失去外负荷，叶轮内流态处于稳定临界状态，流线光滑平顺且紧贴叶轮叶片.叶轮内压力沿着叶片从进口边向出口边逐渐增大.

T2时刻，流量到达零点，反向流量和正向流量数值相等.叶轮内同时存在正向流量和反向流量，流体之间相互冲击，出现流动分离，叶轮流道内出现大小不一的旋涡，内部流态紊乱.叶轮内压力总体上较T1时刻大，压力仍然沿着叶片逐渐增大，变化梯度较T1时刻小.

T3时刻，叶片在两边压强差的作用下，反向流量大于正向流量，与T2时刻相比流线较为稀疏，旋涡消失，叶轮进口边出现多个圆环形流线.叶轮内压力总体上较T2时刻小；由于水的惯性力与叶片旋转产生的离心力作用，使得水流在叶轮边缘堆积形成高压区，叶片工作面压力出现急剧上升，叶片背面压力基本一致，叶轮中心区域出现1个低压中心.

T4时刻，转速由正转速向负转速过渡，与T3时刻对比，中心圆环流线消失.叶轮流道内压力总体上比T3时刻低，沿叶片变化趋势与T3时刻一致，由于正向流量基本为0，叶轮流道由反向流量完全填充，叶轮的转速逐渐降低，因此在叶片背面压力降低，叶片背面尾端出现低压区.

T5时刻，转速为负方向，与T4时刻相比，流道流线平顺光滑，叶轮进口边出现小旋涡.叶轮内部压力总体上比T4时刻高，叶片背面尾端低压区消失，流量和转速方向一致，转变为水轮机工况，水流从泵出口边向泵进口边流动，一部分水流压能转变为叶轮的动能，因此压力随叶片进口边向压力出口边逐渐增大.

T6时刻，转速达到飞逸转速，内部流线较T5时刻复杂多变，叶轮进口处的旋涡逐渐增大并向叶轮出口边移动，内部流态紊乱.由于转速持续增大，压力总体上较T5时刻大，在叶片背面尾端由T4时刻的低压区变为高压区，压力从进口边方向向出口边方向逐渐增大.

2.5 蜗壳截面流速流线分布

蜗壳在管道泵断电过渡过程初期充当出水部件，经历制动工况后，从出水部件转换为进水部件，因此主要对断电过渡过程中蜗壳内部流态进行研究.

T1时刻，管道泵突发断电.蜗壳内部流线平顺光滑，流态处于临界稳定状态，流速总体上处于3～6 m/s.

T2时刻，反向流量等于正向流量.蜗壳内部流线较T1时刻紊乱，泵排出口位置由于正反向流量对冲出现流动分离，产生大量旋涡；第4断面到第8断面之间流速明显小于T1时刻的.

T3时刻，反向流量大于正向流量.蜗壳泵排出口位置流线较T2时刻平顺，靠近基圆区域，流线较为紊乱，第2断面内侧出现旋涡；流速总体上较T2时刻高，靠近基圆区域流速处于低值.

T4时刻，转速到达零点，蜗壳转化为进水部件的临界点.第2断面内侧旋涡消失，靠近基圆区域流线从紊乱变为整齐.流速较T3时刻高，靠近基圆区域流速从低速区变为高速区.

T5时刻，管道泵处于水轮机工况，蜗壳作为进水部件.与T3时刻相比，流线方向改变，由顺时针方向变为逆时针方向.第3断面与第6断面之间，靠近蜗壳外侧，流速较T4时刻降低；靠近蜗壳基圆一侧，流速明显增大.

T6时刻，转速上升至飞逸转速.流线整体变化规律与T5相似.高流速区在T5时刻的基础上继续扩大.

图10 蜗壳流速流线分布特性

3 结 论

1) 管道泵断电过渡过程中，转速呈现出正向减小，反向增大，最后达到飞逸转速并稳定的变化规律；流量呈现出正向减小，反向增大，反向减小并稳定的变化规律；转速与流量存在延迟效应，前者比后者延迟1.24 s到达零点；扭矩呈现出正向减小，正向增大，正向减小最后动态稳定至零点的变化规律.压力脉动先后出现2个波谷，在飞逸阶段达到最大值.

2) 管道泵断电过渡过程初始时刻，进口肘型弯管流线较为光滑平顺；初期在第2弯管内侧和第1弯管外侧出现大旋涡，并向第1弯管方向移动；中期内部流态逐渐平顺，旋涡消失；后期在第2弯管内侧产生小旋涡并向弯管外侧偏移.

3) 管道泵断电过渡过程初期，叶轮内部从稳定流态逐渐产生旋涡并从进口边向出口边移动，叶轮内压力变小；中期叶轮流态逐渐变为稳定，叶片背面压力持续降低；后期叶轮出现从进口边向出口边移动的小旋涡，叶轮内部压力逐渐增大.

4) 管道泵断电过渡过程初期，蜗壳内部流线从平顺光滑变为紊乱，流速逐渐降低，当流量为0时流速降为最低；中期蜗壳内部流线从紊乱变为顺滑，流速增大；后期蜗壳内部流线改变旋转方向，流速进一步增大.