基于改进LMD的泵站摆度信号分析

潘虹，唐魏，郑源，于洋

(1. 河海大学能源与电气学院，江苏 南京 210098； 2. 中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014； 3. 中水东北勘测设计研究有限责任公司，吉林 长春 130062)

局域均值分解(LMD)是SMITH于2005年提出的一种非平稳信号处理方法[1]，其基本思想是将任何一个复杂的非平稳信号分解成多个乘积函数(production function, PF)分量之和，通过提取各个分量的瞬时幅值和瞬时频率来得到信号完整的时频分布.

LMD被广泛应用到旋转机械、电路故障诊断领域.近年来，与小波、熵、深度学习等信号处理与机器学习方法融合应用取得了较好的信号分析效果[2-5].但LMD方法也存在一系列的问题，如LMD中局域均值和包络估计函数是通过平滑相邻极值点获得.但是信号的端点可能不是局部极值点，这样便会造成局域均值和包络估计函数在数据两端失真.在分解高频分量时，由于局部极值点间距较小，端点效应只局限在端点附近，但是低频分量的局部极值点间距变大，端点效应逐渐向内“污染”，严重时分解出错误的PF分量.目前，针对端点效应问题，已经提出许多抑制方法，如镜像映射、波形匹配等，这些方法对抑制端点效应取得了一定的效果，但是在精度或算法适应性等方面存在一定的局限性[6-10].镜像映射法没有考虑信号整体的自然趋势和相似性；波形匹配法对周期重复性信号具有较好的延拓能力，但当信号中存在低频叠加波或调幅信号幅度相差较大的信号时，则误差较大且学习时间过长.

文中从考虑曲线幅值和几何形状相似性出发，提出基于灰色B型关联度和欧氏距离的端点效应抑制方法，通过计算待匹配波形和特征波形的综合距离参数，选择参数最小值对应的匹配波形作为延拓数据，提高LMD分解过程中重构信号精度.

1 LMD端点效应

1.1 端点效应

LMD方法的基本原理是将1个复杂的多分量信号分解为若干个瞬时频率具有物理意义的PF分量和1个残余分量之和.PF分量的瞬时幅值就是包络信号，瞬时频率可由纯调频信号求导获得.

LMD方法中的端点效应是在计算局域均值和包络估计函数时产生.局域均值和包络估计函数是相邻局部极值点均值和包络值的拟合函数.在每次滑动平均法拟合过程中，拟合生成的局部极值点也存在一定误差.由于下一个PF分量是对原信号减去上一个PF分量后进行的又一次筛分，因此拟合误差随着迭代过程不断累积，并从端点附近向数据内部“污染”，最后导致出现错误的分解结果.

1.2 波形匹配法

波形匹配法是一种LMD端点效应抑制方法[11].其基本思想是从原信号中找出最符合端点附近变换趋势的相似波形，实现延拓信号与原信号的光滑过渡.设原信号x(t)，采样数为n.以左端延拓为例，具体步骤如下：

1) 计算出信号所有的极大值点M和极小值N点，对应时间为tmi和tni.

2)x(1),M1和N1构成特征波形，根据x(1)与最靠近左端点的极值点的时间相对位置计算平移波形的起点.

3) 计算x(ti),Mi+1,Ni+1这3点构成的波形与特征波形的误差E(i).

4) 找出最小误差对应的波形，作为匹配波形，将该波形前的数据作为左端延拓数据.若存在多个相等的值，则取与左端距离最远的波形为匹配波形.

右端延拓与左端思路一致.实际计算过程中，可以设置一阈值来控制特征波形与匹配波形的最小误差.

2 端点效应抑制方法

波形匹配法基本思想是从信号内部本身找到与端点处的变化波形最相近的数据段作为端点延拓的参照.这种方法使得延拓波形更加符合原信号的自然发展走势.但是在计算待匹配波形与特征波形的误差时，只是定量给出了待匹配波形和特征波形3个特征点在幅度上的差异，而对波形几何形状的相似性没有度量.因此，文中引入灰色系统理论，提出了基于灰色B型关联度和欧氏距离的改进方法.

2.1 灰色B型关联度

灰色B型关联度通过全面描述曲线间发展过程的异同性和关联程度,根据几何形状的相似程度来判断其联系是否紧密[12].曲线几何形状越接近，灰色B型关联度就越大，反之则越小.其具体计算步骤如下：

设特征序列为X1(k)，待匹配序列为X2(k)，其中k=1,2,…,n.则B型关联度r为

(1)

B型关联度利用位移差反映了2个时间序列发展过程或量级的相近性，利用一阶斜率差和二阶斜率差反映了两序列几何形状的相似性.由于实际应用中待匹配波形的量纲不一定相同，计算前采取标准化变换对原始数据消除量纲.灰色B型关联度对于曲线几何形状的反映比较敏感，但是在衡量曲线幅度上的差异方面不够准确.

2.2 综合距离参数

欧氏距离是衡量曲线幅值差异的定量标准[13].时间序列x={x1,…,xn},y={y1,…,yn}的欧氏距离定义为

(2)

为同时考虑曲线在幅值和几何形状上的差异，文中结合欧氏距离与B型关联度，定义了特征波形和待匹配波形相似度的综合距离参数.为便于比较，对欧氏距离进行了归一化处理.综合距离参数η为

(3)

式中：ε为非常小的正数；D′为归一化后的欧氏距离.综合衡量参数η越小时，代表两段波形相似度越高.

2.3 综合距离法

基于B型关联度和欧氏距离的匹配波形法(简称综合距离法)的左端点延拓步骤如下所示，右端延拓与左端延拓思路一致.

1) 计算信号所有的极大值点M和极小值点.

2) 若第1个出现的极值点为局部极大点，令从左端点到第1个极小点位置的信号为特征波形，左端点到第1个极大点的采样数L.以局部极大点Mi(不包括最后1个极大点)为基点生成待匹配波形，确保每个待匹配波形的Mi与特征波形的Mi重合.待匹配波形长度为n，起点为局部极大点Mi向左移动L个数据.

3) 若第1个出现的极值点为局部极小点，令从左端点到第1个极大点位置的信号为特征波形，左端点到第1个极小点N1的采样数为L.以局部极小点Ni(不包括最后1个极小点)为基点生成待匹配波形，确保每个待匹配波形的Ni与特征波形的N1重合.待匹配波形长度为n，起点为局部极小点Ni向左移动L个数据.

4) 计算所有待匹配波形和特征波形的综合距离参数，找出最小时对应的匹配波形，将该波形前的数据作为左边端点的延拓数据.若存在多个相等的值，则取与左端点距离最远的波形为匹配波形.同理找出最匹配右端点的特征波形，将匹配波形后数据作为右边端点的延拓数据.

5) 应用上述匹配波形选择的方法延拓数据，抛弃两端外延拓数据提取PF分量，重复执行上述步骤直至提取完成所有PF分量.

2.4 端点效应抑制方法评价指标

针对仿真信号和实例信号，根据端点效应伴随的能量泄漏，以分解前后信号的能量变化作为端点效应程度的评价指标，具体方法如下：

1) 计算原信号的均方根有效值

(4)

式中：xi为原信号的第i个组成分量.

2) 计算所有PF分量和残余分量的均方根有效值.

(5)

式中：PFi为信号分解获得的第i个PF分量；k为分解PF分量个数.

3) 计算端点效应的评价指标θ

(6)

θ越大，则说明端点效应影响越大.

针对仿真信号，由于已知信号组成，另建立评价指标δ以体现PF分量与原信号组成分量之间的误差.

(7)

δ越小，端点效应抑制越成功.

3 仿真分析

为比较综合距离法与镜像映射法、波形匹配法对端点效应的抑制性能，下面分别以平稳仿真信号和非平稳仿真信号为例进行具体分析.仿真信号为

x(t)=cos6πt+0.4cos20πt+0.9sin50πt.

(8)

该信号为正弦叠加信号，主要频率为3，10，25 Hz.取样1 024点，采样时间2 s.图1为仿真信号1 LMD分解结果，是3种方法生成的PF分量,即PF1,PF2,PF3，图中上部红色实线为包络线.端点效应评价指标θ和δ见表1.

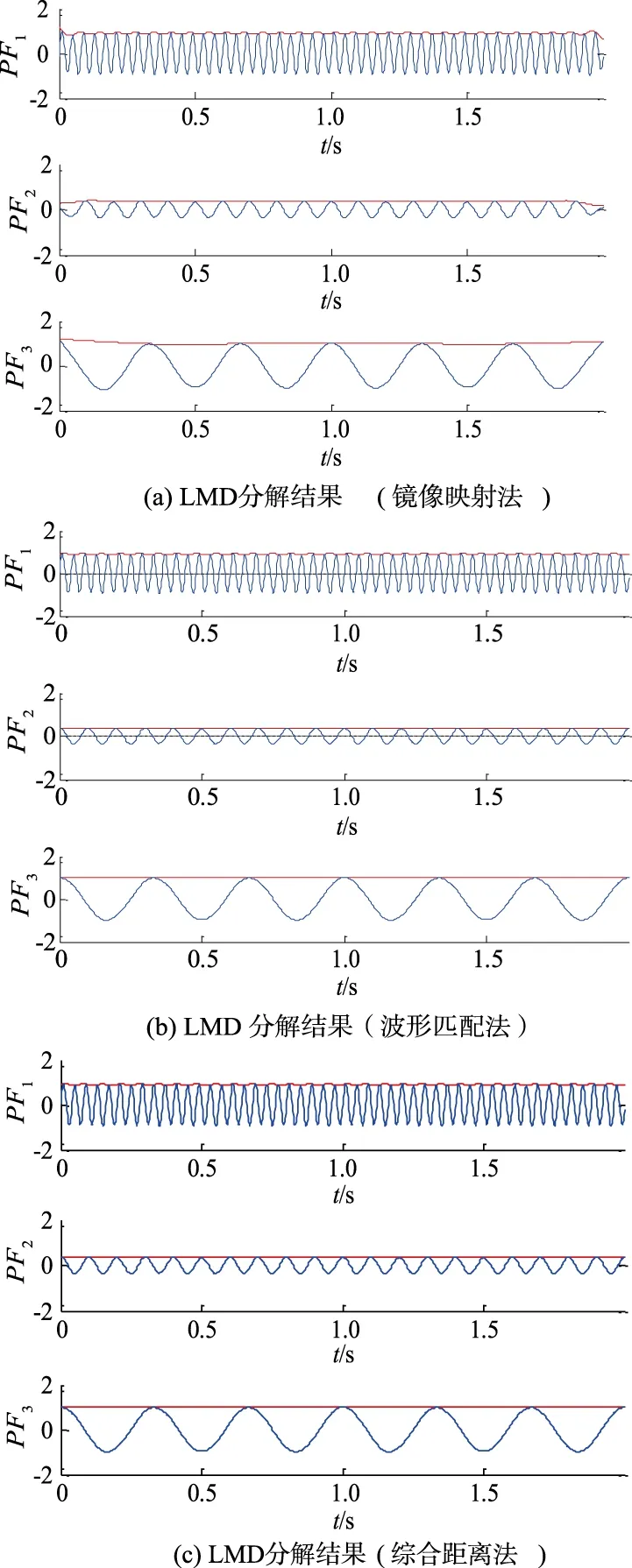
图1 仿真信号1 LMD分解结果

表1 端点处理方法的性能评价

由表1可知，3种方法指标数值均较小，说明端点效应对分解结果影响不大.镜像映射算法的θ最大，说明镜像映射法端点效应抑制效果最差，图1a中PF1和PF2分量两端信号都出现了较大程度的失真，也体现了端点效应的影响.后经仿真信号多次验证，发现镜像映射法对规则信号的端点抑制效果要稍差，波形匹配法和综合距离法适用于信号内部变化具有较强规律的信号.

非线性仿真信号二为

x(t)=(1+0.5cos0.01πt)cos(0.5πt+

2cos0.02πt)+4sin0.000 4πtsin0.12πt.

(9)

信号采样频率为1 Hz，采样时间600 s.信号由2个调幅调频分量组成，一个分量的载频为0.06 Hz并伴有幅值调制，另一个分量的载频为0.25 Hz附近并带有频率为0.01 Hz的频率调制.

利用镜像映射法、波形匹配法及综合距离法对仿真信号二进行LMD分解，结果如图2所示,图中上部红色实线为包络线.波形匹配法包络线由于幅值过大未绘制.由图可见，所有方法获得的PF1分量都对应载频为0.25 Hz左右的调幅调频信号，且瞬时频率图中清楚显示0.01 Hz的频率调制现象.PF2分量对应了载频为0.06 Hz的调幅分量.根据数学描述，PF1和PF2分量在左端点处的幅值应该分别为1.5和0，而实际分解结果与瞬时频率的数学表达式存在较大差异.

对该非平稳信号而言，波形匹配法效果最差.在图2b中，右边的端点效应比较严重，PF分量幅值数量级高达106.为了显示PF分量的波形，调整PF1和PF2分量的y轴坐标范围为[-5,5].PF3是由于端点效应产生的虚假模态.此外，波形匹配方法所得的PF1和PF2分量的瞬时频率在左右端点的波动幅度也远大于其他方法.镜像映射法效果仅优于波形匹配法，在时间为500 s处信号幅值和瞬时频率都出现了较大突变.

表2为端点处理方法的性能评价，即列出了3种方法的评价指标θ和δ.由表可知，波形匹配法的性能最差，信号右端点出现了较大误差，评价指标均远大于其他方法，取最大值1.镜像映射法能量指标θ最小，但是其波形误差指标δ较大，这一点与图2a中500 s处PF分量的幅值大幅度波动吻合.综合距离法对仿真信号二端点效应的抑制性能最好，其中综合距离法的波形误差仅为0.008，证明分解所得的PF分量与原信号0.25 Hz和0.06 Hz的组成分量基本一致.

图2 仿真信号2 LMD分解结果

表2 端点处理方法的性能评价

经多次仿真信号试验，结果表明：镜像映射法对平稳信号和非平稳仿真信号端点效应的抑制效果都较差，但是该方法操作简单，分解速度上具有明显的优势；波形匹配法主要适用于信号内部变化具有较强规律的平稳信号，对非平稳信号会出现较大误差；综合距离法由于从幅值和几何形状上这2个方面综合考虑了特征波形的匹配识别，对非平稳信号可以取得较好的分解结果.

4 试验信号分析

以某泵站主轴摆度信号为例，分析综合距离法对实际信号的适用性.机组叶轮直径3.19 m，设计抽水扬程4.2 m，设计总抽水量66 m3/s，机组额定转速136.4 r/min.摆度信号由IN-085电涡流传感器采集，经CRAS振动信号采集与分析处理系统处理获得，采样频率为512 Hz，采样时间8 s.图3为主轴径向摆度信号时域图，图中A为幅值.

图3 主轴摆度信号时域图

图4为水泵主轴摆度信号LMD分解结果.为提高分类精度和速度，分解前对原信号进行了去除趋势项和降采样处理，采样频率降为64倍转频.应用镜像映射法、波形匹配法和综合距离法对信号进行分解，结果如图4所示.其中PF2根据相关分析判断为虚假分量.

由图4可知，PF1分量中同时出现了2.273Hz的转频和转频倍频，这是LMD分解常见的模态混叠现象.此处主要根据PF1分量时域图比较各方法对端点效应抑制情况.镜像映射法在7.5～8.0s的时间段上PF1分量波形失真，波形匹配法在0～1s的时间内PF1分量波形明显失真，综合距离法的分解结果没有出现此类现象，波形基本保持一致.3种方法算法评价指标见表3，由于该主轴摆度信号为实际工程信号，指标无法计算.由表3可知，与镜像映射法和波形匹配法相比，综合距离法的评价指标明显减小.利用文中提出的LMD改进方法对多个水电站振摆信号进行了试验验证，结果与上述水泵主轴摆度信号分析结果一致.总的来说，PF分量示意图和评价指标都表明综合距离的端点抑制方法性能较好，可以有效抑制端点效应对分解结果产生的波形失真现象.

图4 水泵主轴摆度信号LMD分解结果

表3 摆度信号端点处理方法的性能评价

5 结 论

1) 文中针对局域均值分解方法存在的端点效应问题，提出了基于灰色B型关联度和欧式距离的改进抑制方法，克服了传统镜像映射法和波形匹配法无法兼顾幅值和几何形状差异的不足，适合用于非平稳信号时频分析.

2) 利用基于灰色B型关联度和欧式距离的综合距离法分析泵站主轴摆度，端点效应评价指标远低于传统方法，证明利用该方法分解信号准确率更高.但在分析过程中，也发现局域均值分解方法存在的模态混叠问题，在很大程度上影响了信号特征提取的效果，这方面问题有待进一步研究.