固有应变法在钢板三角感应加热变形计算中的应用

张雪彪，鹿想，刘海涵

(大连理工大学 a.运载工程与力学学部船舶工程学院；b.工业装备结构分析国家重点实验室，辽宁 大连 116024)

在船厂，帆形板的水火弯板成形多采用三角加热工艺，即火炬在靠近板边时进行摆动加热，从而增大板边的加热面积和温度，以得到大的板边收缩量，达到帆形板的成型要求。对于感应热源的水火弯板工艺，见图1，当感应器在板边处进行摆动加热时，也可以获得同样的收边加热效果。

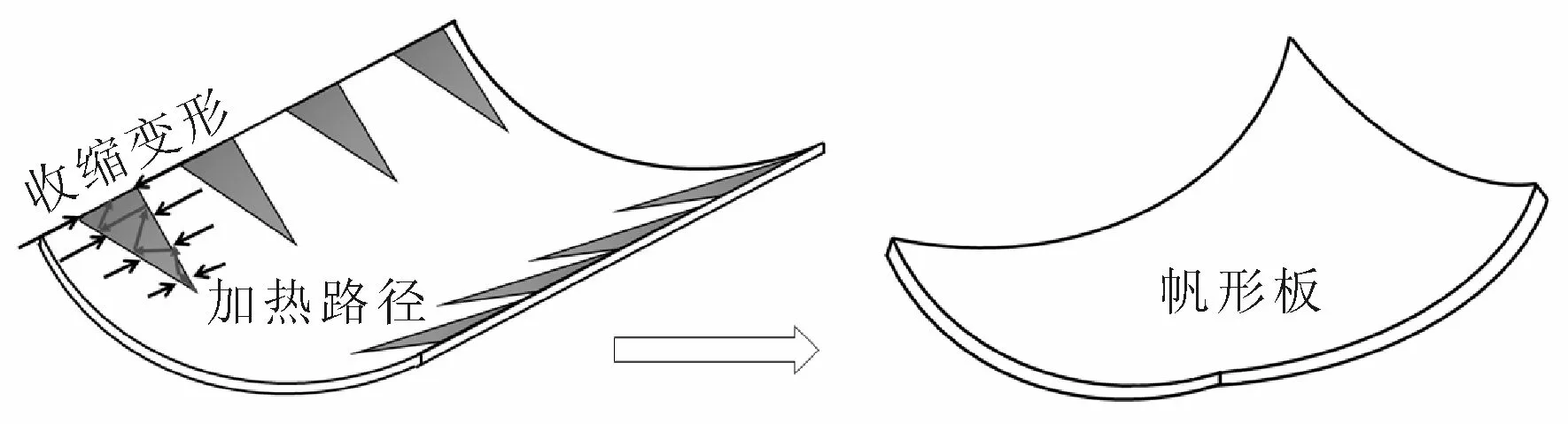
图1 帆形板变形过程

对于钢板多加热线的变形计算问题，采用电磁-热-结构耦合的有限元模型进行计算是困难的，因为模型复杂，计算量巨大，所以研究者多采用基于固有应变法的弹性有限元模型进行计算。有学者等使用圆盘-弹簧模型作为三角加热过程的简化热弹塑性力学模型，在三角加热的固有应变区域内进行分区域的等效载荷加载[1]。有学者提出计算三角加热形状和位置的算法，建立加热形状和残余变形的函数关系。相关的研究均采用火焰热源的圆盘-弹簧模型来计算固有应变，力学模型不适用于除圆形外的其他感应器形状，也不能简单地应用于钢板感应加热工艺。为此，考虑采用钢板电磁-热耦合的热弹塑性模型得到加热线附近的塑性应变值，然后对塑性应变进行积分，从而获得固有应变沿加热线的分布规律，在进行弹性有限元分析时考虑固有应变的分布规律，使之符合钢板三角感应加热的变形特点。

1 加热实验与数值模拟

针对钢板的三角感应加热工艺，文献[3]在大量实验的基础上确定了三角感应加热的摆动加热路径，并建立了基于辊弯板的钢板三角感应加热的电磁热耦合模型，该数值模型为进一步应用固有应变法预测钢板变形提供了条件。

1.1 实验布置

在大连理工大学造船工艺实验室进行加热实验，辊弯板的曲率半径为2 000 mm，钢板尺寸及加热的工艺参数见表1，实验方案布置见图2，距离加热线中间偏右侧20 mm处的P点为温度测量点，通过测量加热线两侧11对测量点的距离变化得到加热前后的横向收缩量。

表1 感应加热的工艺参数

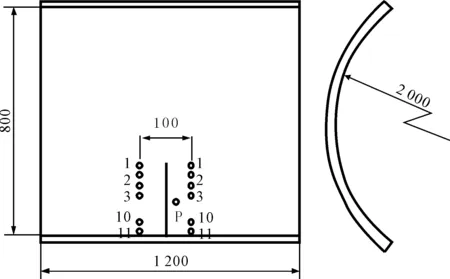
图2 实验布置和测量方案

三角感应加热路径见图3，即先线状加热而后折线加热，从而实现三角加热的效果。直线部分210 mm，速度v1为8 mm/s，折线加热区域的长度90 mm，速度v2为9 mm/s。加热过程中的局部现场见图4，加热结束后的钢板表面见图5，在靠近板边处的加热线区域大致呈三角形状。

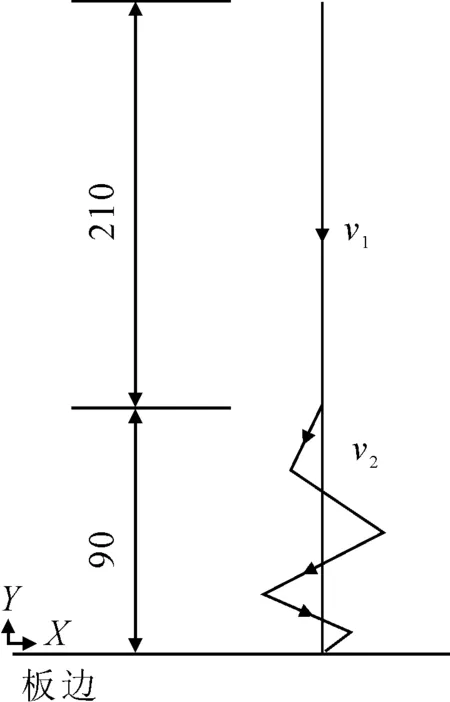
图3 三角感应加热路径示意

图4 三角感应加热图

图5 三角感应加热后钢板表面

1.2 数值模拟

利用文献[3-4]的辊弯板移动式感应加热电磁-热耦合有限元模型对加热过程进行模拟。辊弯板的移动式感应加热示意见图6，移除空气包后的横截面模型见图7。

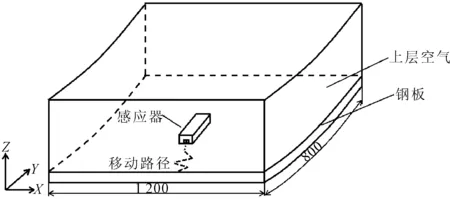
图6 辊弯板的摆动感应加热示意

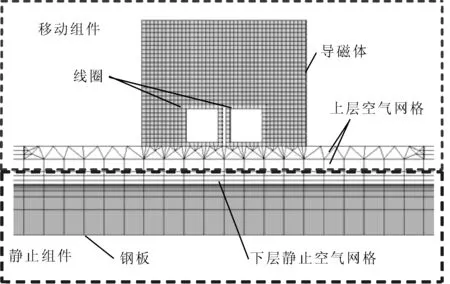
图7 钢板-感应器-空气局部网格

整个加热系统分为两部分：①由感应器、远场空气包，以及上层运动空气组成的移动组件；②由钢板和下层静空气组成的静止组件。该模型通过节点约束方程技术，实现了感应器、空气间隙和钢板之间相对移动的计算域求解过程，计算钢板的温度和变形，揭示钢板和感应器之间的电磁耦合效应。

P点温度实验值和数值计算值的比较见图8，横向收缩的实验值与数值计算结果的对比见图9，两者的平均相对误差为15.3%。横向收缩和温度的变化情况都与实验值一致，横向收缩量的分布从板里到板边呈逐渐增大的趋势，表明所设计的三角感应加热的路径是合理的。

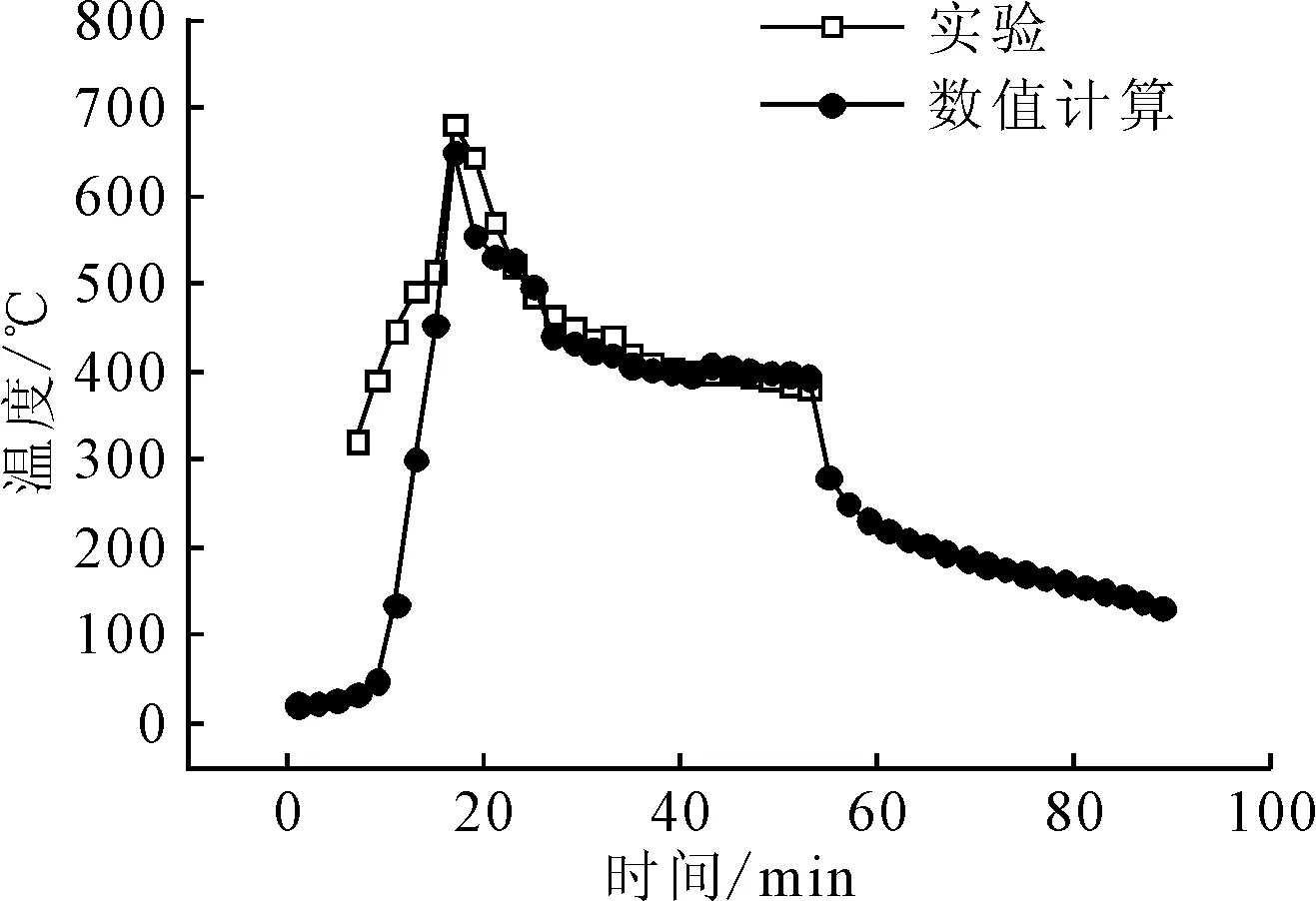
图8 P点温度的数值实验对比

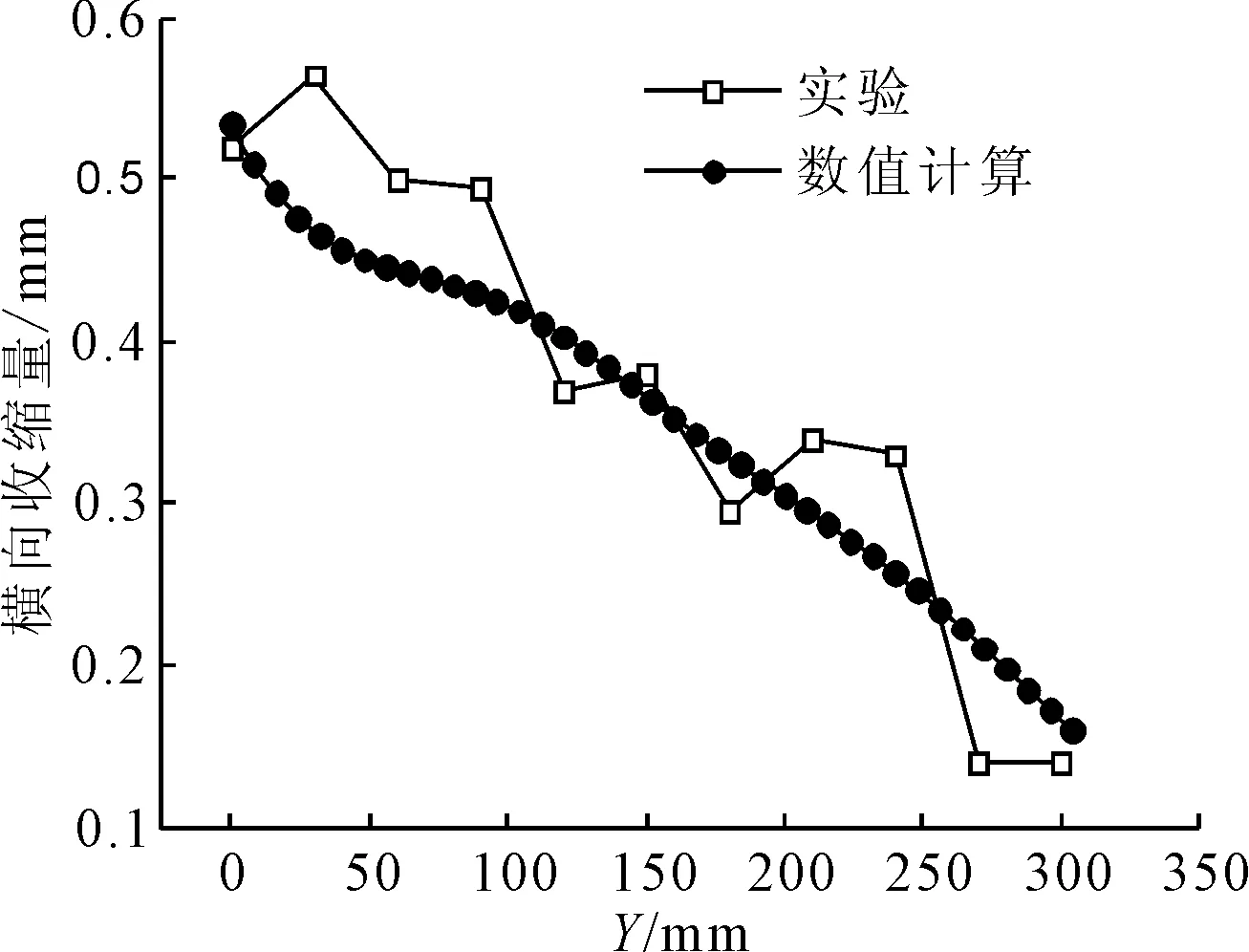
图9 横向收缩量比较

2 固有应变法应用

根据固有应变法，焊接过程中引起的无弹性的应变是固有应变ε*[5]，即

ε*=ε-εe

(1)

式中：ε为总应变量；εe为弹性应变。

固有应变是塑性应变εp、热应变εt和相应变εθ三者之和，即

ε*=εp+εt+εθ

(2)

在实际加热过程结束后，热应变为零，如不考虑相变应变，固有应变就是塑性应变值。为了得到钢板在加热过程中的固有应变，将塑性应变在横截面上积分得到固有应变之和，从而得到固有应变值[6]。

2.1 钢板三角感应加热固有应变的计算

对于辊弯板的三角感应加热过程，对数值模拟得到的各个截面的塑性应变εp进行积分，得到横向固有应变之和Wx和纵向固有应变之和Wy。

(3)

(4)

式中：εx为横向固有应变；εy为纵向固有应变；A为固有应变区域沿垂直于加热线方向的截面积。

对于壳单元或实体单元模型，在加载区域宽度为b，加载深度为h的情况下，定义加载区域的材料具有x、y方向的热膨胀系数，热膨胀系数值αx、αy分别为

(5)

(6)

在进行固有应变加载时使用温度载荷法进行加载，在ANSYS软件中设置材料的各向异性热膨胀系数，然后施加单位温度载荷，进行一次弹性计算获得变形结果。温度与应变的关系为

ε=α·Δt

(7)

式中:α为材料热膨胀系数;Δt为单位温度载荷，设置为1 ℃;ε为产生的热应变数值。

沿着加热线每隔15 mm选取一个截面，共20个截面，提取每个截面的节点塑性应变值，积分后得到横向和纵向固有应变积分曲线见图10。

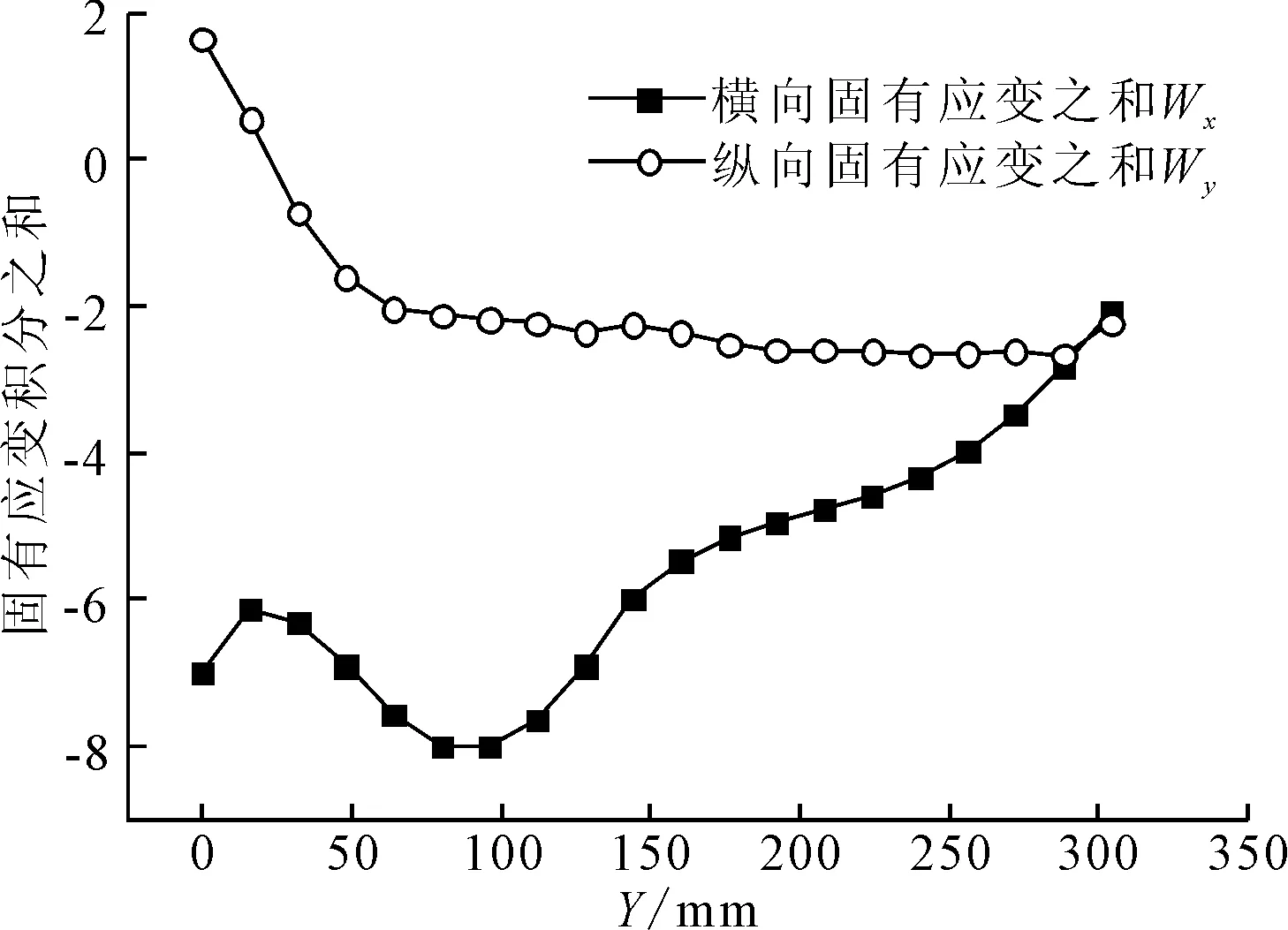
图10 固有应变积分

可以看出横向和纵向固有应变积分曲线没有明显的变化规律，因此加载固有应变时必须考虑其实际的分布规律。这一点不同于焊接产生的固有应变，因为焊缝长度足够长，超过临界焊接长度后固有应变有稳定值[7]，可以用平均固有应变来进行加载。

首先加热线长度是有限的；另外，三角加热的加热路径决定了钢板加热后产生非均匀的固有变形分布。鉴于此，在弹性有限元计算时须加载实际的固有应变分布，而不能采用平均固有应变。

2.2 固有应变的加载

各截面处的塑性应变云图见图11。在板边Y=0 mm处，固有应变集中分布区域宽度最大109.0 mm，Y=300 mm处宽度为44.2 mm，宽度值从板里向板边逐渐增大。

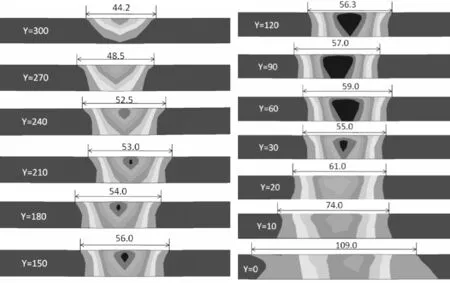
图11 各截面横向塑性应变云图

钢板弹性有限元分析模型见图12。

图12 钢板整体网格图

单元类型是SOLID 45单元。在加热线附近的单元进行了网格细化，网格尺寸为1 mm，其他非加热区域的网格为5 mm。在弹性有限元计算时采取图13所示的加载方法，在每个加载段内分别加载不同的热膨胀系数，经过多次计算，发现梯形加载和矩形加载的变形结果差别很小，而矩形加载却更方便，这与文献[8]结论一致。因此，将固有应变区宽度设置为50 mm。根据文献[9]推导的考虑角变形的固有应变加载深度公式，此处加载深度为14 mm。

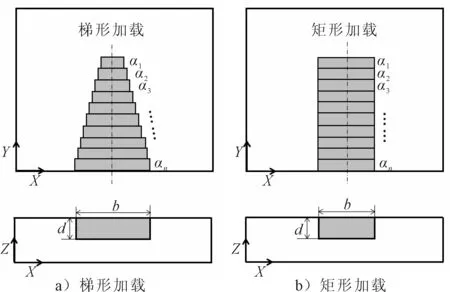
图13 固有应变加载方法

图14a)为横向变形云图，图14b)为垂向变形云图。弹性有限元计算的结果与热弹塑性有限元模型的结果十分相近，计算时间约1 min，变形形状也符合三角加热的变形特点。

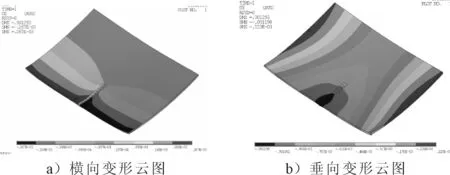
图14 弹性有限元分析的位移云图

横向收缩量的对比见图15，与实验值相比较弹性有限元分析结果相对误差为13.84%。加热线中心线处的垂向位移对比见图16，两者的相对误差为3.75%。面内变形和面外变形结果都符合工程要求，表明计算方法是可靠的。

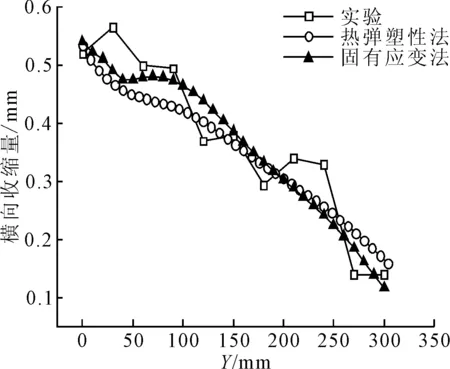
图15 横向收缩量比较

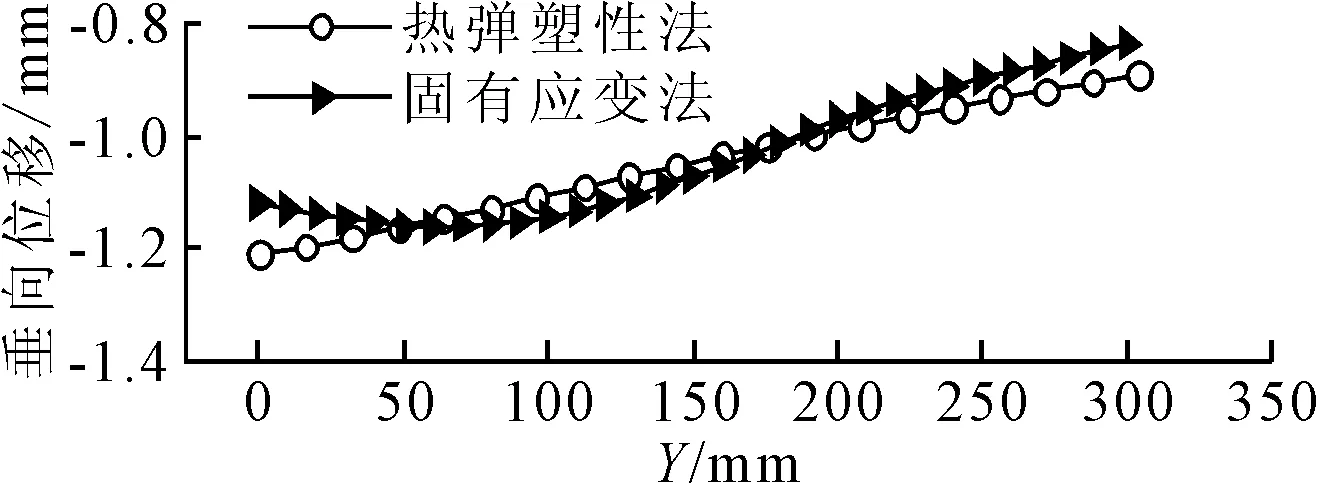
图16 垂向位移比较

3 辊弯板三角感应加热变形计算

帆形板成形时需要在钢板上布置加热线，基于固有应变法的弹性有限元分析方法计算钢板的变形。因为钢板表面有多条加热线，在忽略加热线彼此之间影响的前提下进行变形预测，实验时设置加热线间距为200 mm。

实验用钢板尺寸为1 200×800×20 mm，辊弯半径2 000 mm，实验方案见图17。

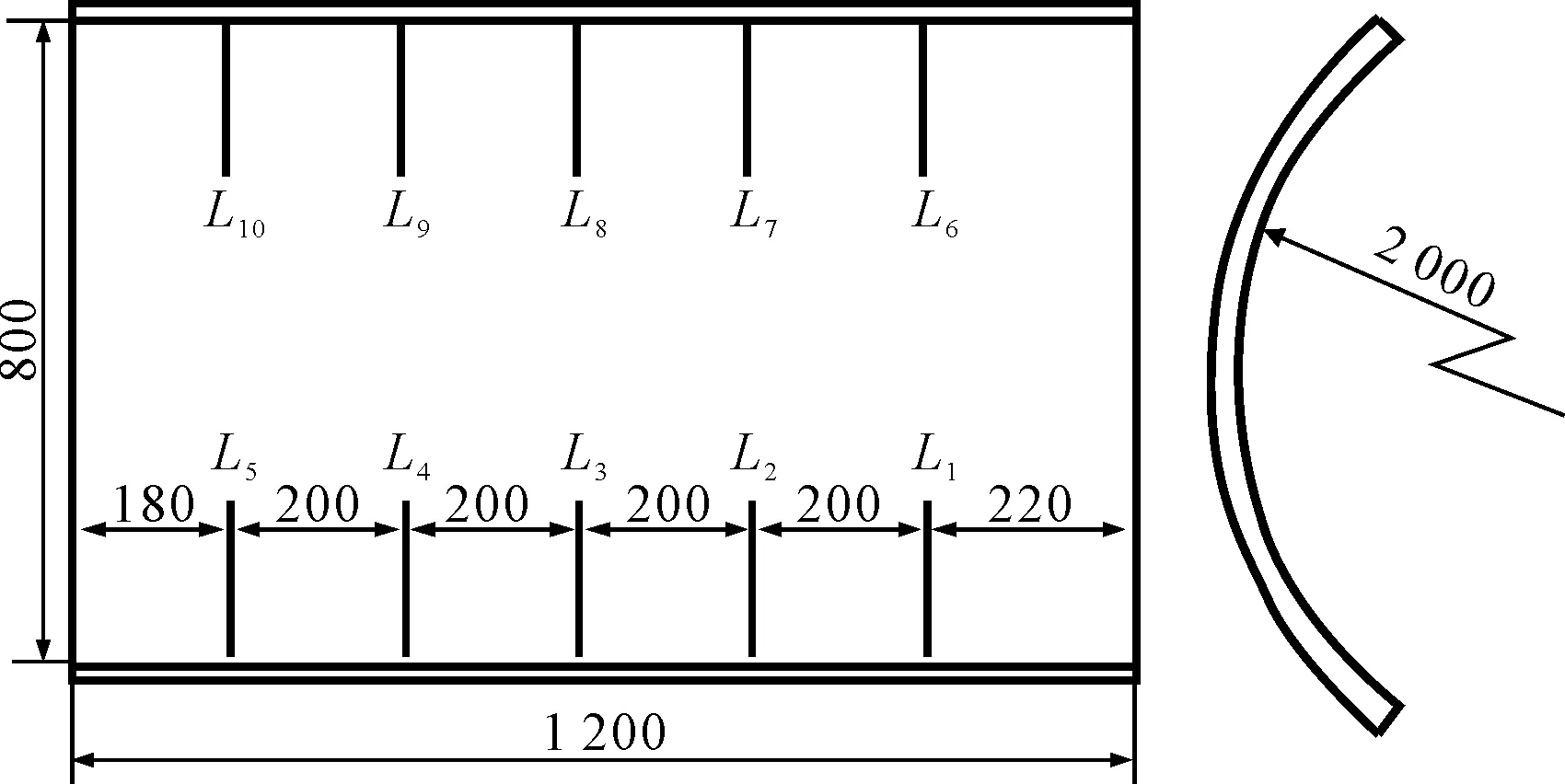
图17 辊弯板三角感应实验布置

采用靠近板边处进行摆动加热的三角加热方式，共10条加热线，加热线的速度信息见表2，加热线长度300 mm，空气间隙9 mm，加热功率50 kW。钢板在全部加热线完成之后的加热效果见图18。

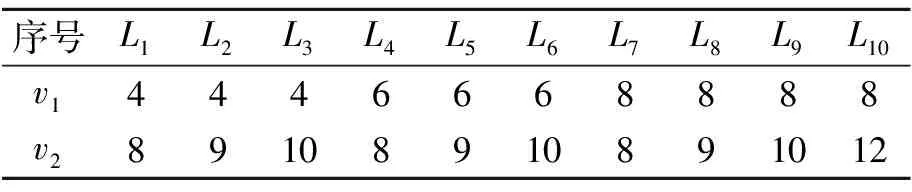
表2 加热线速度信息 mm/s

图18 加热后的钢板

辊弯板的弹性有限元模型见图19，单元类型为SOLID45，均匀划分钢板网格，长度、宽度方向的网格尺寸均为10 mm，板厚方向的网格尺寸为0.5 mm。使用温度载荷法进行固有应变的加载，在各个加热线处的单元施加X、Y方向的热膨胀系数，限制刚体位移约束四个顶点的X、Y、Z方向的自由度。

图19 钢板有限元模型

测量线示意图见图20。钢板曲面的测量采用徕卡掌上全站仪S910进行测量，测量精度1.0 mm，测量现场见图21，测量曲板坐标点数据后进行数据处理得到挠度值。钢板的垂向位移云图见图22，钢板中间区域的垂向位移较大。横向变形云图见图23，收缩量在板边处较大，钢板整体呈现为帆形。

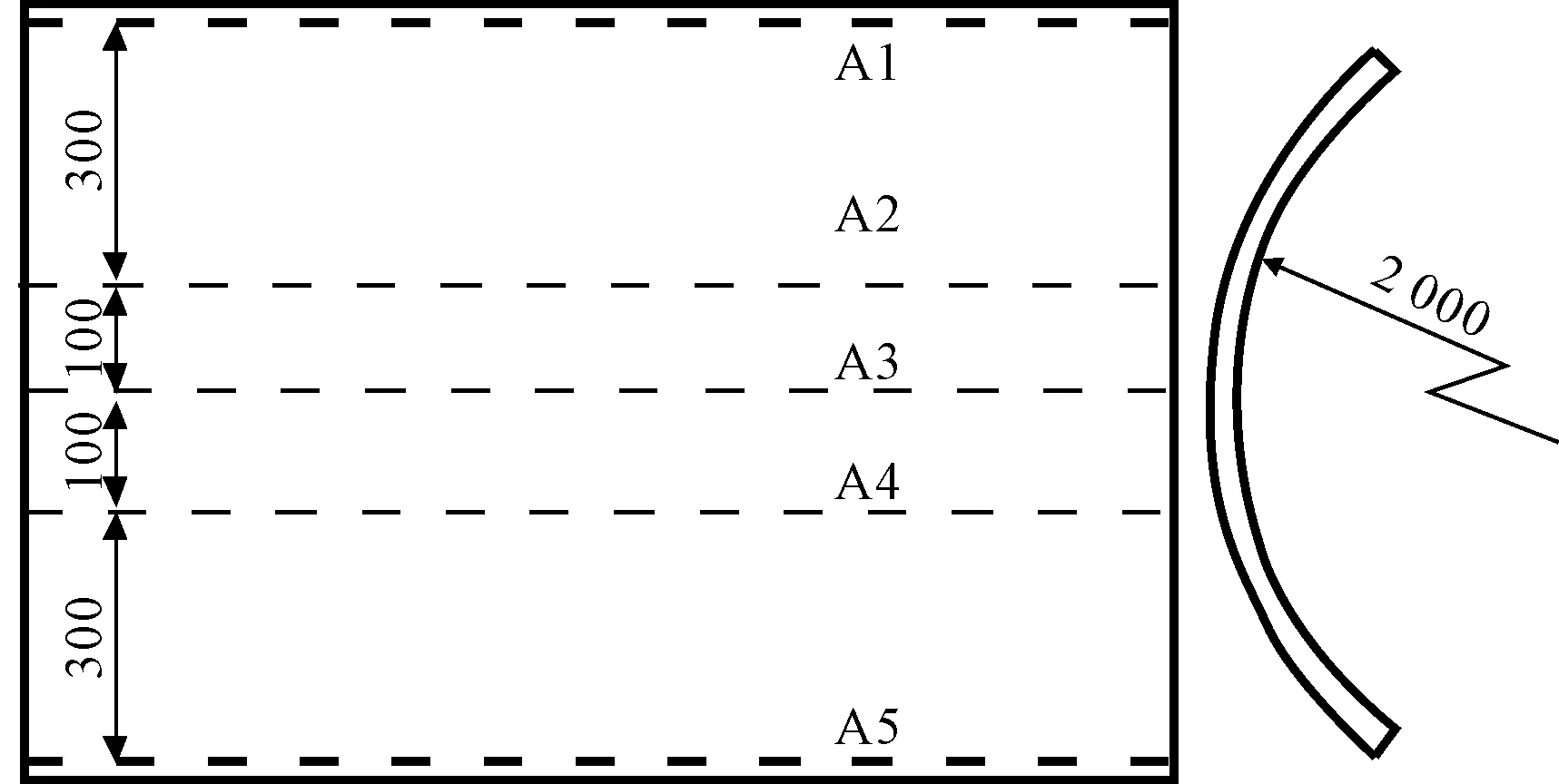
图20 测量线布置示意

图21 徕卡掌上全站仪S910测量钢板曲面现场

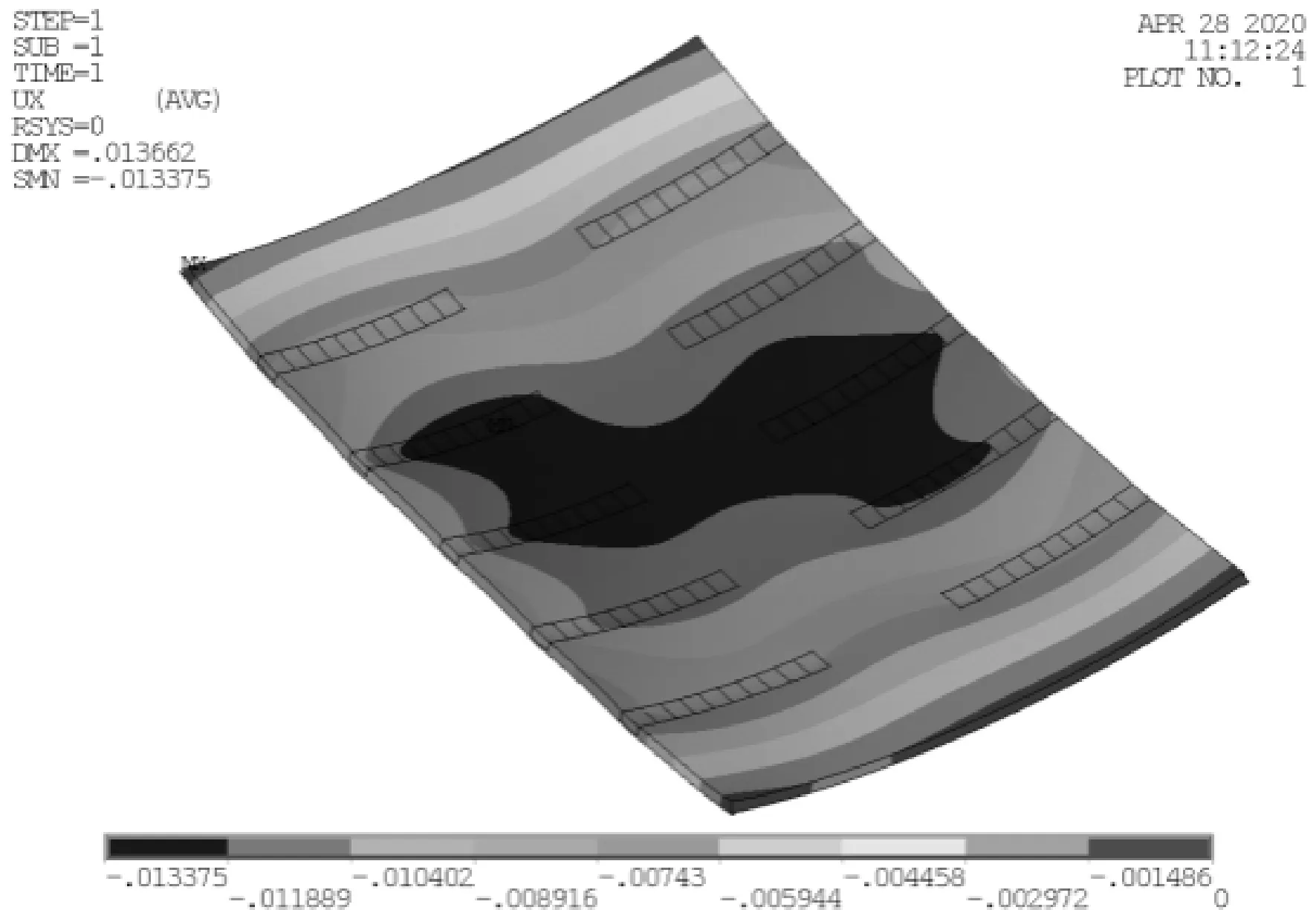
图22 垂向变形云图

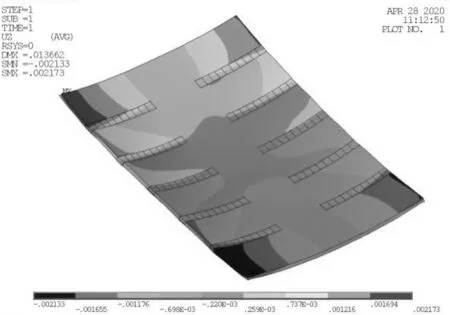
图23 横向变形云图

各测量线的挠度测量值和计算值的对比见图24，各计算值和实验值一致。其中A1线与A5线位于纵向板边位置，因为板边处的固有应变值较大，计算出的垂向位移有波浪型的变化。A1～A5线的实验值和计算值的平均相对误差分别为：14.2%，10.7%，7.8%，13.4%，13.1%，误差均在工程允许的范围内。

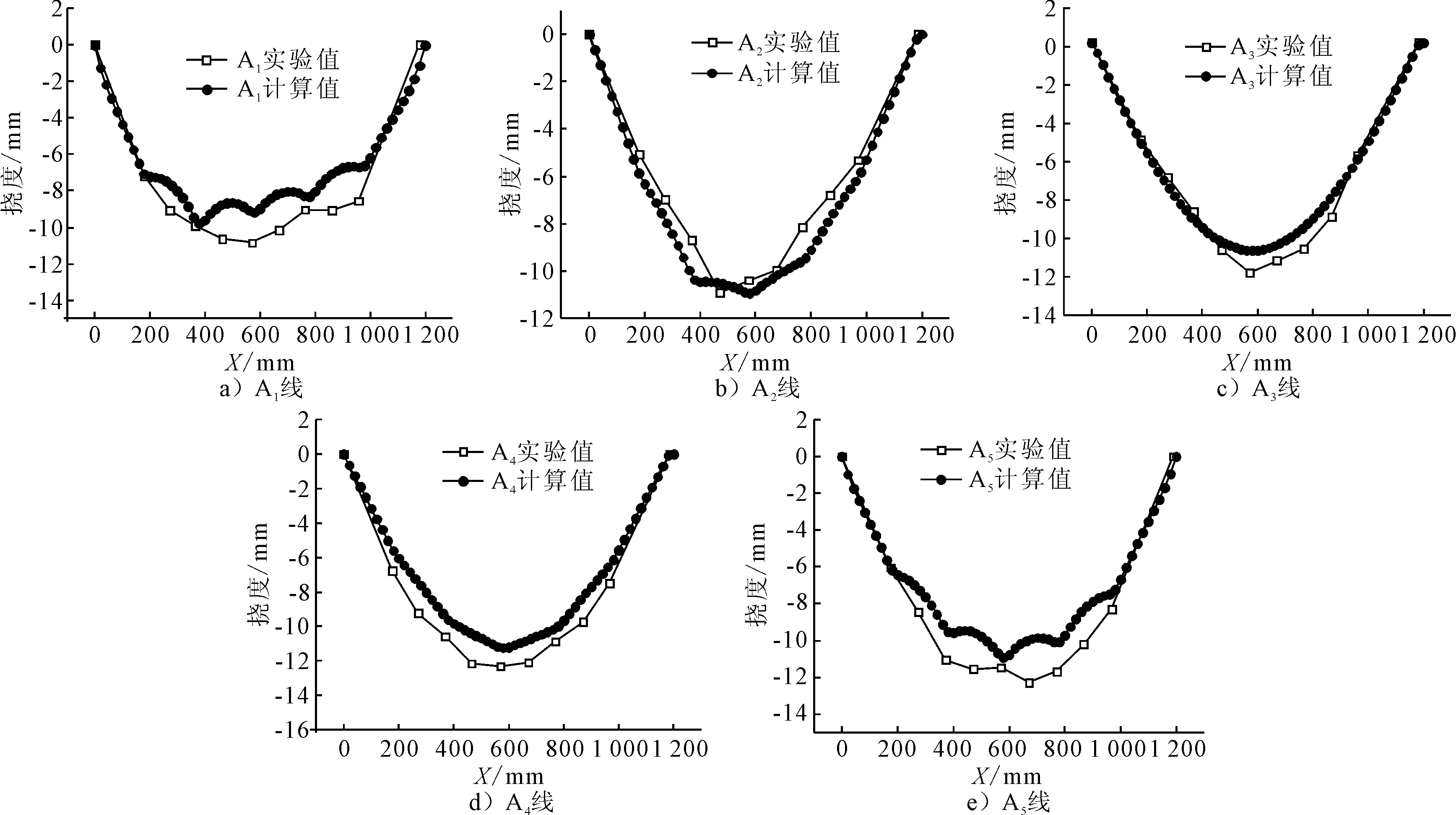
图24 测量线的挠度值比较

对于多条加热线的辊弯板变形计算，在忽略加热线之间影响的前提下，基于固有应变法的弹性有限分析可以实现钢板的整体变形计算，计算时间短，可以用于水火弯板工艺的整体变形预测。

4 结论

钢板的三角感应加热工艺产生复杂的固有应变分布规律，在进行固有应变的弹性有限元计算时在加载区域内需要加载实际的固有应变值，而不是平均固有应变。同时，进行辊弯板的多条加热线的感应加热实验，使用建立的固有应变加载模型进行弹性有限元计算，计算的钢板挠度值与实验值相符，整体变形效果与实验一致。