车削粗糙表面法向接触刚度仿真研究
伍伟敏,卢耀晖
(1.湖南财经工业职业技术学院,湖南 衡阳 421002;2.国防科技大学智能科学学院,湖南 长沙 410073)
0 引 言
法向接触刚度对机械系统稳定性具有重要影响[1]。目前,对于精密仪器整体刚度的接触仿真而言,大都忽略了粗糙结合面的法向接触刚度参数,进而造成仪器整体刚度偏低的设计缺陷。由于缺少准确的法向接触刚度参数,难以开展高端装备机械结构设计工作。如何准确有效地获取机械结合面法向接触刚度是亟需解决的问题[2]。并且,随着机床加工精度的提高,机械系统中多数连接端盖、连接法兰等机械加工表面都是采用精车的加工方式进行[3-4]。因此,本文针对车削表面法向接触刚度进行研究。
对于粗糙表面法向接触刚度的获取主要存在理论解析、有限元仿真及实验测试3种方法。理论解析方法是采用模拟粗糙表面表征实际粗糙表面,通过对模拟粗糙表面上单个微凸体的接触分析,继而结合微凸体的表面统计学理论,实现对粗糙表面法向接触刚度的解析计算。具有代表性论著的是1966 年Greenwood 与Williamson 提出GW 模型[5]。此后Chang 对GW 模型进行了改进,基于微凸体塑性变形的体积守恒理论提出了CEB 模型[6]。Kogut基于球形微凸体的有限元分析,提出了KE 模型[7]。国内西安理工大学张学良团队对法向接触刚度的理论解析模型进行了较为深入的研究[1,8-9]。虽然理论解析对于法向接触刚度的研究取得了很大进展,但是仍存在以下两点缺陷:模拟粗糙表面假设方面,目前理论解析模型中的模拟粗糙表面与实际加工表面偏差较大[10];微凸体接触变形计算方面,对于微凸体的受力变形分析过程,并未考虑微凸体之间的相互作用以及基体变形等因素。
对于粗糙表面法向接触刚度的实验测试方法,由于实验样本的多样性、传感器精度高以及实验条件苛刻等问题,导致实验成本高,实验数据覆盖面少等缺点。
随着有限元技术的发展,有限元方法的有效性以及低成本的绝对优势近年来在各领域得到广泛的应用[9]。本文基于车削运动学原理,实现了车削表面微观形貌点云数据的获取。运用逆向建模方法实现了车削表面模型的构建。采用Abaqus 有限元仿真软件对车削表面法向接触刚度进行了仿真分析。并且,通过改变车削加工参数获得了不同粗糙度参数的粗糙表面,继而探讨了车削加工参数对法向接触刚度的影响规律。
1 有限元仿真模型的构建
区别于传统宏观结构的有限元仿真分析,对于微观机械结合面法向接触刚度接触仿真研究的重点在于如何基于表面微观形貌的点云数据实现有限元仿真模型的构建。法向接触刚度有限元仿真流程如图1 所示。

图1 有限元仿真流程图
如图1 所示,对于法向接触刚度(后文皆用接触刚度表示)的有限元仿真,首先需要基于车削运动学原理获取表面微观形貌数据,并形成点云数据文件。基于点云数据文件生成特征曲面,并将特征曲面采用逆向建模软件生成实体特征。至此实现了基于表面形貌数据到三维实体模型的构建。之后,将三维实体模型导入到有限元仿真软件进行接触分析,最终得到接触刚度的有限元结果。
1.1 点云数据获取
基于车削运动学原理,本节针对车削表面微观形貌的形成过程进行介绍。图2 所示为基于车削运动学原理的车削表面理论形貌形成原理图[2]。文献[11]对车削加工表面微观形貌进行了实验研究,对比分析了理论形貌与实际形貌的误差。研究结果显示,两者相对误差的最大值小于4%。由此可见,两者相对误差较小。因此,对于车削加工表面理论形貌的残余高度Rt的探讨,本文仅讨论刀具的刀尖圆弧半径r以及进给量f两个加工参数。并且上述3 个参数有式(1)所示关系。


图2 车削表面理论形貌建模原理图
将加工参数作为初始参数,将刀具的刀尖圆弧半径r与车削进给量f代入式(1),采用Matlab 软件编制程序,即可实现对车削表面微观形貌的仿真。图3 所示为刀尖圆弧半径r=0.2 mm、进给量f=0.2 mm 加工参数下车削表面微观形貌仿真图像。

图3 r=0.2 mm、f=0.2 mm 时车削表面微观形貌仿真图像
篇幅有限,本文仅对刀尖圆弧半径r=0.2 mm、进给量f=0.2 mm 加工参数下车削表面仿真图像进行展示。工件半径为1.5~2.5 mm 的圆环区域。之后的处理流程也以此工况条件为例进行介绍。
按照上述流程,通过改变初始加工参数,即可得到不同工况条件下车削表面微观形貌。同时可以得到表面微观形貌数据。基于表面形貌数据,形成点云数据文件,为后期车削仿真模型的构建奠定基础。
1.2 仿真模型构建
基于1.1 节得到的车削表面形貌的点云数据文件,本节采用Solidworks 逆向建模软件实现从点云数据到仿真模型的构建。具体流程介绍如下:采用Solidwork 插件ScanTo3D 导入点云数据文件,采用网格处理向导构造网格曲面。经由上述流程,构造出了特征曲面模型之后,构造圆柱体其余的3 个表面,然后进行曲面缝合,创建实体特征。
刀尖圆弧半径r=0.2 mm、进给量f=0.2 mm 加工条件下仿真模型如图4 所示。为降低后期仿真计算的时间成本,高度方向只取2 mm。仿真模型建立之后,输出成通用格式,便于后期将模型导入到有限元软件进行接触仿真分析。

图4 r=0.2 mm、f=0.2 mm 条件下仿真模型
2 法向接触刚度有限元仿真
基于仿真模型,本节对车削表面法向接触刚度的有限元仿真流程进行介绍。本文选用有限元分析软件ABAQUS[12-13]对1.2 节建立的仿真模型进行有限元仿真分析。
车削表面法向接触刚度的有限元仿真也包含前处理、分析计算以及后处理三个步骤。首先将1.2节建立的模型导入到有限元分析软件之中,并且为实现后期不同层次网格密度的划分,定义截面将导入的模型拆分成两个部分。并且定义材料属性:弹性变形过程的弹性模量为210 GPa,泊松比为0.3。塑性变形的应力应变对应关系如表1 所示。

表1 塑性变形的应力应变对应表
由于理论解析方法中,对于粗糙结合面的法向接触刚度参数的获取是将粗糙表面与刚性平面进行的接触分析。为方便后期引入后期理论模型解析结果进行对比,采用粗糙界面与刚性平面相互接触的接触仿真方式。因此,此处需要定义一个刚性平面。
在相互接触的两部件设置完成之后,对两部件进行装配,两部件装配需留有0.01 mm 的间隙,保证两部件在接触分析之前避免干涉。下面对于摩擦函数与摩擦系数的选取依据进行阐述。由于相互作用设置的是粗糙表面与刚性平面的表面与表面接触方式。因此,接触属性设置为切向行为。摩擦函数采用罚函数,相对其他函数而言,具有更好的收敛性。对于钢铁材料而言,查表可知[13],摩擦系数为0.15。
载荷的施加采用刚性平面强制位移的加载方式。圆柱体底面采用完全固定的设置,刚性平面在竖直方向设置0.03 mm 的位移。两部件的边界条件如图5 所示。

图5 边界条件设定示意图
在设定边界条件之后,对两部件进行网格划分。前期在导入部件的过程中,将圆柱体部件拆分为两个部分,图5 中也可以看出,圆柱体被拆分为两个部分。
采用为边布种设定方式对圆柱体进行网格划分,3 个边界的单元尺寸分别设定0.05 mm、0.2 mm 及0.8 mm。网格单元形状采用C3D10H 型四面体单元。网格划分示意图如图6 所示。

图6 网格划分示意图
为方便后期数据处理,设定历程输出。法向接触刚度的表达式如式(2)所示。

式中:ΔF——法向载荷变化量,N;
Δx——位移变化量,mm;
A——名义接触面积,mm2。
由上式可以看出,法向接触刚度参数的获取需要已知3 个参数。其中名义接触面积为已知条件。对于仿真分析需要输出法向载荷的变化量以及位移的变化量。因此,对于历程输出的设定,选定刚性平面的位移量以及圆柱体底面的反作用力两个参数。结合两个参数,经后期数据处理,即可得到粗糙结合面的法向接触刚度。
待完成上述设定之后,提交作业进行分析即可。
3 结果与分析
按照第2 节仿真流程即可获取得到刚性平面的位移量以及圆柱体底面的反作用力两个参数。按照如式(2)所示对得到的数据进行处理,即可得到不同载荷作用下法向接触刚度的变化曲线。
图7 所示为刀尖圆弧半径r=0.2 mm、进给量f=0.2 mm 加工条件下法向接触刚度随结合面载荷的变化曲线。并且为保证仿真数据的可靠性,引入KE 模型的理论解析结果进行对比分析。KE 模型初始参数的获取及计算流程按照文献[6]所述流程进行。
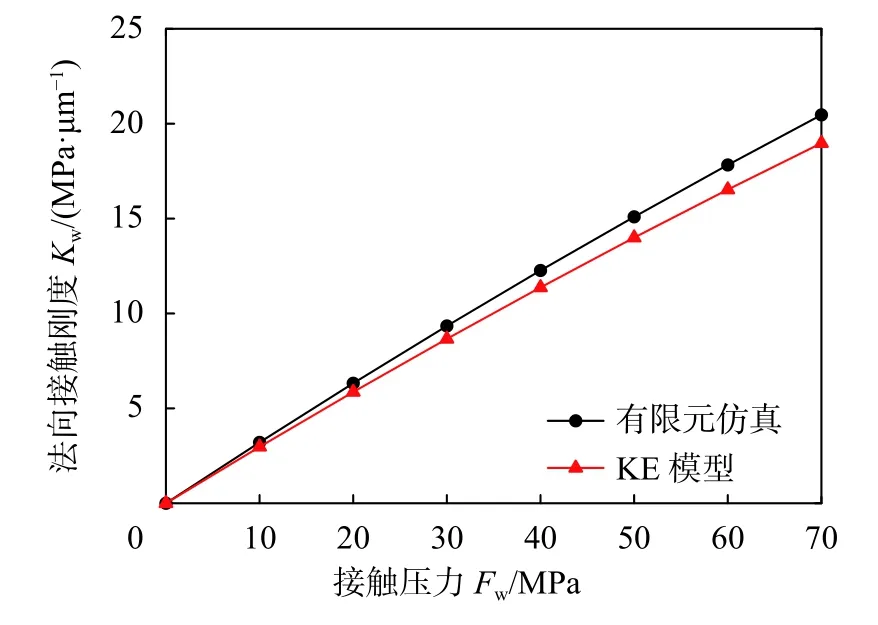
图7 KE 模型结果与有限元仿真对比结果
由图7 可以看出,KE 模型解析结果与本文有限元仿真结果具有相同的变化趋势,即法向接触刚度随接触压力的增大而逐渐增大。在接触压力Fw=70 MPa 时,此时KE 模型解析结果与有限元仿真结果的法向接触刚度具有最大值,分别为18.978 MPa/µm 与20.467 MPa/µm。在相同接触压力条件下,KE 模型的理论解析结果小于本文有限元仿真结果。
结合车削表面微凸体的接触变形过程进行分析。在接触初期(Fw<10 MPa),微凸体顶端首先参与接触,KE 模型结果与本文有限元结果基本一致。随着接触压力的增大,由于微凸体之间的相互作用,致使法向接触刚度的增大。但在KE 模型建立过程中假设部分,忽略了微凸体之间的相互作用,致使随着接触压力的增大,本文结果要大于KE 模型结果。
下面针对不同工况条件下车削表面法向接触刚度的有限元仿真结果进行分析。由于车削加工表面理论形貌的残余高度Rt只与刀具的刀尖圆弧半径r、车削进给量f有关,因此本节将以上两个参数作为变量,对车削表面法向接触刚度随接触压力的变化关系进行探讨分析。
按照第1 节与第2 节分析流程,对不同参数下法向接触刚度进行有限元仿真研究。刀尖圆弧半径取0.2,0.4,0.8 mm;进给量分别为0.1,0.15,0.2 mm。图8 所示为刀尖圆弧半径r=0.2 mm 在不同进给量条件下法向接触刚度随结合面载荷的变化曲线。

图8 不同进给量下有限元仿真结果
由图8 可以看出,不同进给量下,法向接触刚度具有相同的变化趋势,法向接触刚度随接触压力的增大而逐渐增大。在接触压力Fw=70 MPa 时,此时不同进给量下法向接触刚度具有最大值,分别为20.467,28.890,34.993 MPa/µm。在相同接触压力条件下,法向接触刚度随进给量的增大而逐渐减小。
结合第1 节中基于车削理论得到的表面微观形貌进行分析。在相同刀尖圆弧半径的条件下,随着进给量的增大,车削表面残余高度Rt逐渐增大,表面粗糙度数值的增大,进而导致法向接触刚度的减小。
图9 所示为进给量f=0.2 mm 在不同刀尖圆弧半径条件下法向接触刚度随结合面载荷的变化曲线。

图9 不同刀尖圆弧半径下有限元仿真结果
由图9 可以看出,不同刀尖圆弧半径下,法向接触刚度具有相同的变化趋势,法向接触刚度随接触压力的增大而逐渐增大。在接触压力Fw=70 MPa 时,此时不同刀尖圆弧半径下法向接触刚度具有最大值,分别为20.467,22.326,24.187 MPa/µm。在相同接触压力条件下,法向接触刚度随刀尖圆弧半径的增大而逐渐减小。
同样结合第1 节中基于车削理论得到的表面微观形貌进行分析。在相同进给量的条件下,随着刀尖圆弧半径的增大,车削表面残余高度Rt逐渐减小,表面粗糙度数值的减小,进而导致法向接触刚度的增大。
4 结束语
1)本文基于车削运动学原理,实现了车削表面微观形貌点云数据的获取。运用逆向建模方法实现了特征曲面与三维模型的构建。采用Abaqus 有限元仿真软件对三维模型进行了接触分析。
2)对比分析了有限元仿真结果与KE 理论模型解析结果。对比结果显示,在相同工况条件下,理论解析结果与仿真结果结果的变化趋势相同,法向接触刚度随接触压力的增大而逐渐增大。在相同接触压力条件下,KE 模型结果小于有限元仿真结果。
3)对比分析了不同加工参数下的仿真结果。在相同接触压力条件下,法向接触刚度随车刀刀尖圆弧半径r的增大而逐渐增大,随车削进给量f的增大而逐渐减小。

