基于温度场分析的航空大型烘箱温度性能研究
熊稚莉,陈 波,蔡豫晋,顾 伟,唐海燕
(成都飞机工业(集团)有限责任公司,四川 成都 610092)
0 引 言
烘箱是航空材料制造热加工工艺过程中的重要设备,在消除材料氢脆、涂层固化改善、产品热老化试验、复合材料固化成型等工序中起到非常重要的作用[1-2]。温度均匀性是衡量烘箱温度性能的重要指标[3],国内外许多规范,如AMS2750[4]、CPS8100[5]对温度均匀性的测量都有明确的要求,并且温度均匀性测试的符合情况是Nadcap(国家航空航天和国防合同方授信项目,national aerospace and defense contractors accreditation program)等三方审查中重要的考核依据之一。随着航空材料向大型整体化制造方向发展[6],越来越多的大型烘箱将投入于航空大型零件制造使用。在烘箱的安装调试过程中,需要特别关注温度性能。在高温测量领域已有不少关于改善热加工设备温度性能的研究。马伟[7]总结了影响航空制件专用热处理炉系统精度和温度均匀性的因素,通过实验论证了如何运用PID 调节改善温度均匀性。高伟[8]提出了影响空气循环炉温度均匀性的因素及相关改善方法。姚纯[9]从加热系统、控制系统、保温系统等方面介绍了影响烘箱温度均匀性的原因及其改善方法。
控制传感器的位置对烘箱整体温度性能的影响很大。在工程应用中,对于未知温度分布情况的烘箱,一般根据工程经验估计温度中值位置,将控制热电偶布置于此点,再结合设备调测过程中的温度均匀性分布结果,对控制传感器位置进行修正。在有些复杂情况下,例如烘箱加热系统、空气循环系统设计不合理时,需通过优化控制传感器位置和控制参数来弥补设计的先天不足,否则容易造成温度过冲、整体温度分布偏移、歪斜等情况。
目前,已有不少学者利用有限元分析法对复合材料热压罐工艺固化成型中温度场的分布进行研究,例如林家冠等[10]等利用FLUENT 流体分析软件对航空复合材料构件热压罐成型工艺的温度场和流场特性进行了模拟分析;花蕾蕾等[11]以复合材料构件热压罐框架式成型模具为对象,应用有限元方法,分析模具温度的分布。但目前并无针对航空大型烘箱,利用仿真分析手段改善其温度性能的相关研究。
鉴于此,本文以航空大型烘箱为对象,通过仿真模拟烘箱内部温度场分布,为合理布置控制传感器的位置提供科学依据,进而提高烘箱的温度性能。
1 仿真模拟
本文以一大型航空零件制造用烘箱为研究对象,烘箱尺寸(宽×深×高)为6 m×4.8 m×4.1 m,有效工作区尺寸(宽×深×高)为5 m×3.1 m×2.5 m,顶部均匀分布着12 个搅拌风机。烘箱壳体采用钢框架结构,内膛骨架设计断热桥,保证良好的绝热性能;炉体保温材料采用耐高温型非石棉保温材料,保温层材料厚度不小于150 mm,具有良好的保温隔热效果。本烘箱工艺使用温度范围:50~85 ℃,本文重点测试烘箱在50 ℃与85 ℃设定值处的温度性能。
1.1 烘箱物理模型
烘箱是一个双层薄壁结构,由内膛、壳体组成,为了便于后续CAE 模型的分析计算,需对烘箱进行简化,处理后的烘箱几何模型如图1 所示。

图1 烘箱简化后的三维数模
1.2 烘箱温度场有限元分析模型
为了使流体计算过程趋于稳定,本文对烘箱的热量交换方式进行简化:取加热器所在烘箱侧壁顶部为热量和风的入口,烘箱顶端搅拌风机为其出口。烘箱壳体外壁为绝热壁,此壁面几乎与外界不存在热传递;内膛侧壁为双侧壁面,即壁面的内外区域均是计算区域,对于此种壁面不需要设定任何热力学参数,CAE 软件会根据壁面的材料属性、流体速度以及温度自动计算流体与壁面之间的对流换热系数等热力学参数,只需设定壁面的厚度材料参数等。利用仿真软件CFD 提供的网格前处理工具CFDViscart 对CAD 模型计算域进行网格划分,所生成的网格类型为笛卡尔自适应网格,图2 为烘箱网格划分示意图。

图2 烘箱的网格划分
1.3 仿真结果
本文构建的有限元分析模型设定的升温模式为:30 min 内从室温15 ℃升至设定温度50 ℃,当烘箱升至设定温度后保温40 min,从升温开始至结束共70 min。
图3 为29 min 时烘箱整体温度场分布情况,选取原因是该时刻处于升温即将结束而未完全结束阶段,可以看出烘箱的温度分布在310~317 K(37 ℃~44 ℃)之间,烘箱内温度分布差异较大。差异具体体现在:侧壁温度较高,中上部温度适中,侧边局部区域温度较低。图4 为60 min 时烘箱整体温度场分布情况,该时刻处于达到设定值后保温一段时间的阶段,可以看出烘箱温度分布在319~324 K(46~51 ℃)之间,侧壁及底部温度较高,除此之外的中间区域温度在321~322 K(48~49 ℃),表明该时刻烘箱内部中间区域的温度场趋于一致。此外,从仿真结果细节可以观察到,烘箱侧壁分布着三条竖直温度带,该竖直温度带低于侧壁整体温度。该情况与实际情况是符合的:烘箱采用拼接方式搭建,连接处的焊缝容易造成烘箱内温度与外环境热交换,导致接缝处温度低于侧面整体温度,因此分布着三条低于侧面整体温度的竖直温度带。
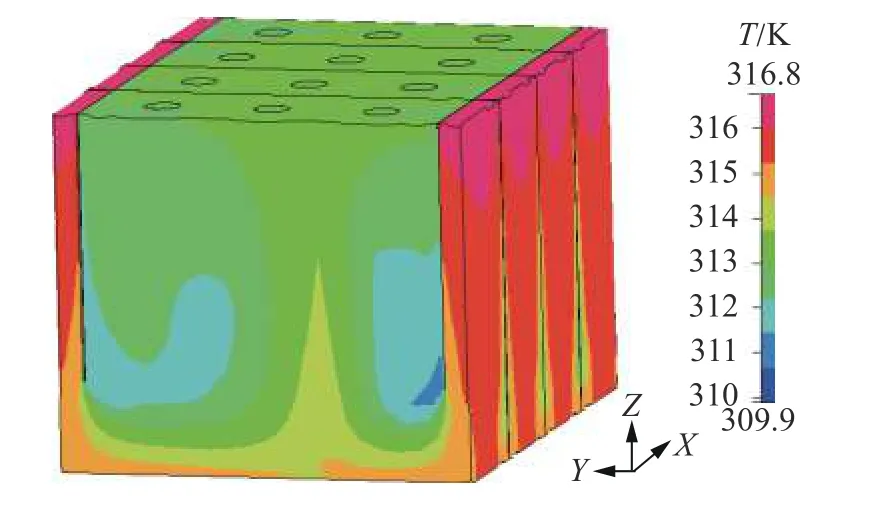
图3 29 min 时烘箱整体温度场分布

图4 60 min 时烘箱整体温度场分布
根据烘箱内部的热分布仿真结果可以得出结论:1)烘箱侧壁温度较高,而烘箱内部中间区域的温度场趋于一致,温度变化梯度小;2)无论是温度升温或保温阶段,烘箱内部中间区域中上部位置处温度适中,靠近整体温度场的中值。
2 试验验证
2.1 控制热电偶的选型与位置确定
目前烘箱的温度控制系统一般采用PLC 程序,控制传感器将温度信号采集后输入主控单元,通过PID 运算得出控制量,再通过调压模块来控制电加热管的加热,其流程如图5 所示[12]。在控制传感器的选型中,由于热电偶具有测量范围大、测量精度高、结构简单、响应时间快、成本低的优势,因此选用热电偶作为控制传感器。
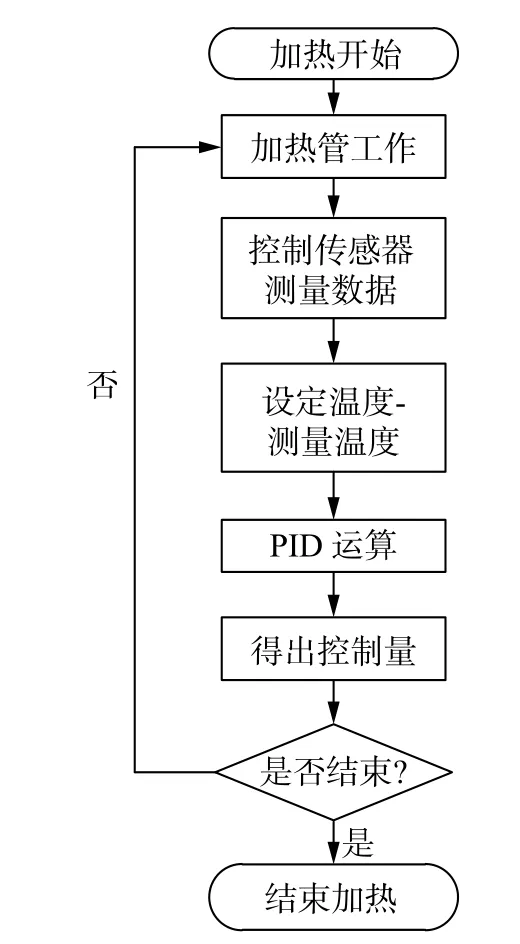
图5 加热程序流程图
在烘箱升温过程中,控制热电偶选择不合理将会极大影响其内部温度性能,直接表现为:温度均匀性超出容差。控制热电偶不合理,包括型号规格与安装位置两个方面。控制热电偶一般为铠装廉金属热电偶,而测试热电偶一般采用同分度的易耗型廉金属热电偶。由于易耗型热电偶测量端裸露,响应速率比控制偶更快,在升温过程中控制仪表的温度总是滞后于实际温度,致使整体温度偏高。因此需要将控制偶布置于合理位置,弥补差异性。若选用外径更粗的控制热电偶,会使控制仪表温度的滞后性更加明显,容易出现温度过冲现象。另外,若控制热电偶位置不合理,当安装于烘箱内部温度较高处,会造成炉膛整体温度偏低;反之,当控制偶位于温度较低处,则会造成整体温度偏高。
如图6 所示为理想状态下烘箱的温度曲线变化情况,当控制偶达到设定温度时,温度低点温度很快能够到达容差下限,经过控制系统一段时间调整,烘箱内所有温度均在容差范围内,保持稳定。但是,当控制传感器选型和位置不合理时,容易出现温度过冲。如图7 所示,在升温过程中控制偶的温度滞后于烘箱实际温度,且远小于烘箱内温度高点的升温速率,从而造成温度最大值超过容差上限。在航空零件制造生产中,温度过冲现象是不允许发生的。
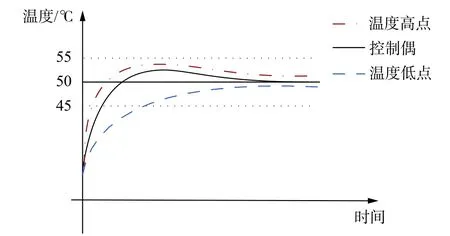
图6 理想情况下的烘箱温度曲线

图7 控制传感器不合理造成的温度过冲
本烘箱采用外径规格为φ3 mm 的控制传感器,该种传感器响应速度快,可以很好地使温度值反馈至控制系统,避免温度超差。此外,由于烘箱体积较大,设计为2 区控温,每个控温区需装备1 支控制热电偶。根据上一章节中对烘箱内部的热分布仿真结果,可以得出以下结论:1)本烘箱的有效工作区应处于烘箱空间的中部,与烘箱底部、侧壁板保持一定距离;2)沿烘箱的前端和后端将有效工作区平均分为控制1 区和控制2 区,控制热电偶应处于控温区的中部。考虑到不影响机翼、垂尾等大型零件的摆放,在高度上控制热电偶应位于控温区的上部中间部分。
2.2 试验安排
烘箱工艺温度容差为±5 ℃,根据高温测量规范要求,共计布置40 个温度均匀性测试传感器,如图8 所示,现场试验图见图9。其中编号1#和编号2#测试传感器靠近控制热电偶,其测量端与控制热电偶的测量端距离不大于10 mm。本试验系统所包含的所有测试设备及传感器符合AMS 2750 规定的现场测试仪器与传感器精度要求[13],可保证测试数据的准确性。
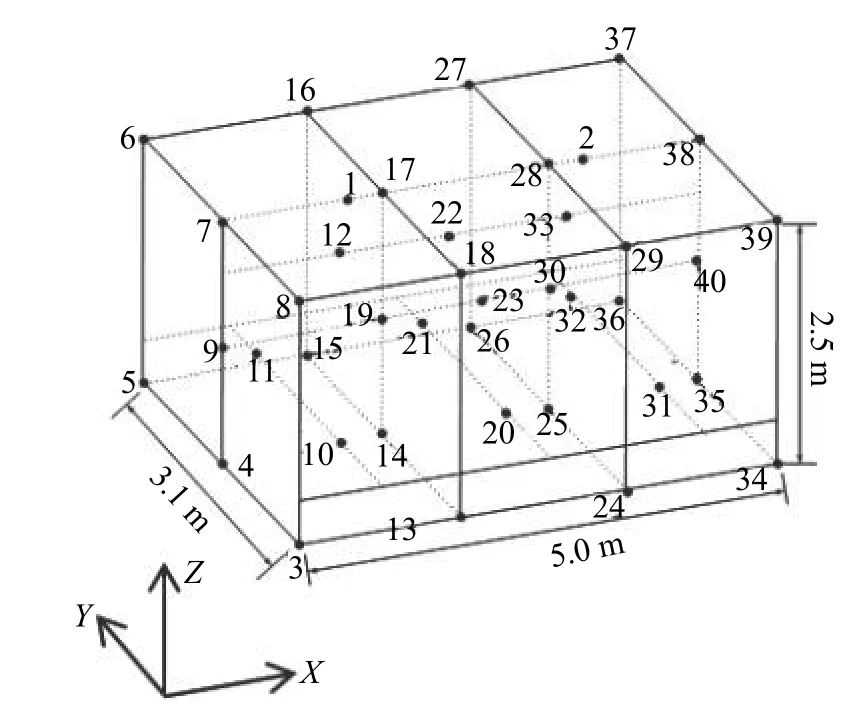
图8 温度传感器布置图

图9 现场试验照片
2.3 试验结果及分析
2.3.1 试验与仿真结果的比较
根据行业标准,当烘箱内部所有传感器达到设定值并保持稳定后,数据采集应持续至少30 min,采集间隔不超过2 min。本文以50 ℃为例,分别沿烘箱的X轴、Y轴、Z轴方向各取两组测试点,将传感器所采集的温度数据去除误差后,计算稳定状态30 min 期间的平均值,比较测试的平均值与仿真的平均值在空间上的差异。
沿着X轴方向,取编号为8#、18#、29#、39#与6#、16#、27#、37#两组测试点;Y轴方向,取编号为3#、4#、5#与34#、35#、36#两组测试点;Z轴方向,取编号为14#、19#、17#与25#、30#、28#两组测试点,测试值与仿真值的结果如图10~图12 所示。

图10 X 轴方向的两组测试点对比
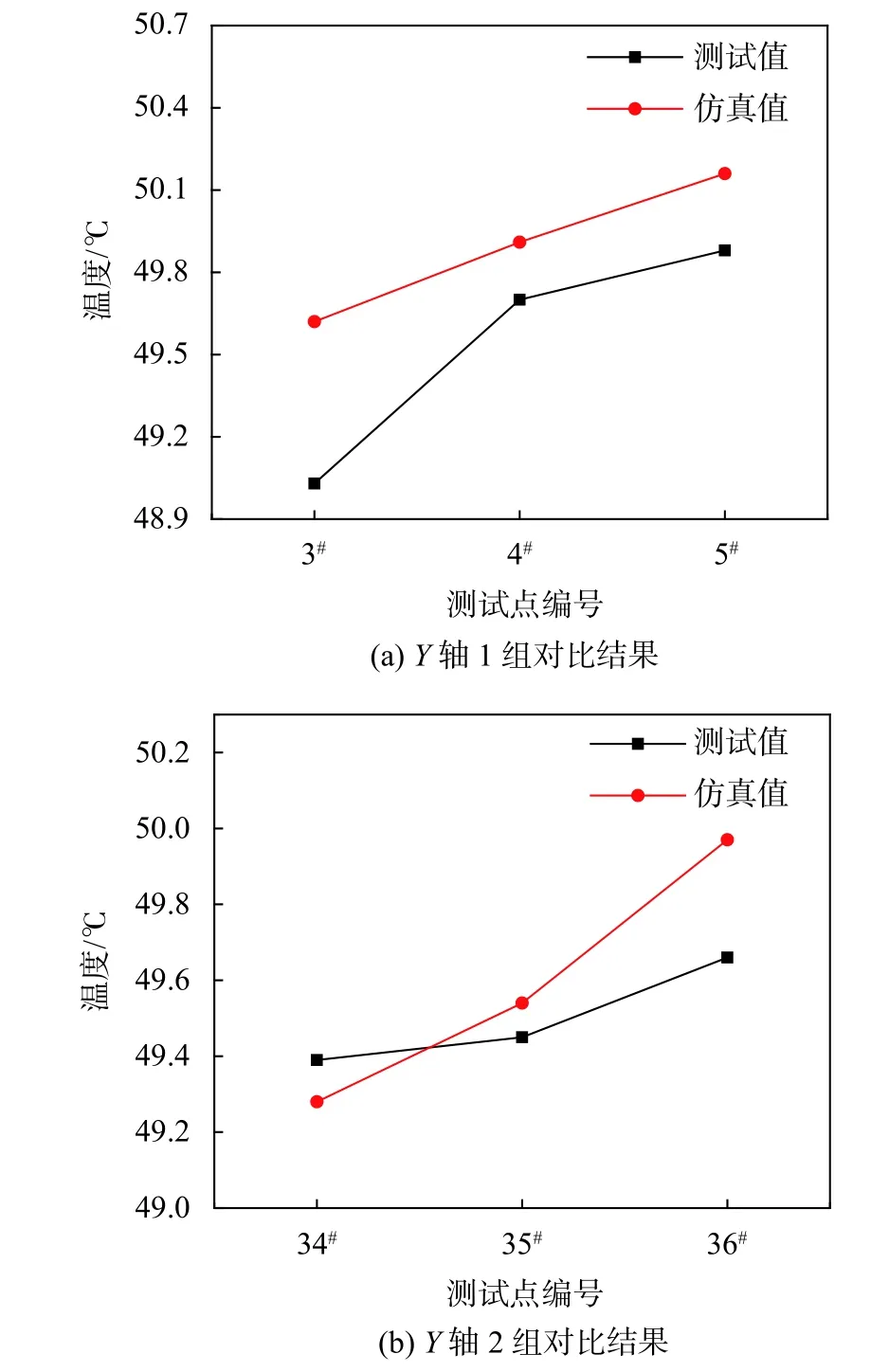
图11 Y 轴方向的两组测试点对比
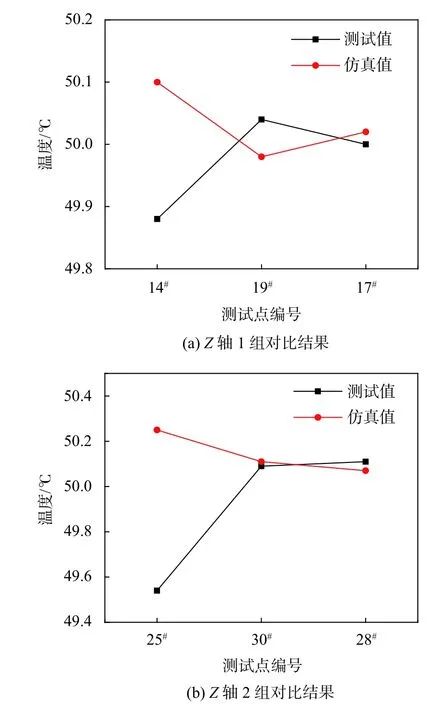
图12 Z 轴方向的两组测试点对比
从图10 中可以看出,测试值和仿真值在X轴方向无明显分布规律,温度范围在49.9~50.6 ℃。在Y轴方向,测试值与仿真值较为接近,均显示出了规律性:沿着Y轴方向,温度逐渐上升。在Z轴方向,测试值与仿真值的差异明显,图4 所示的烘箱整体温度场分布和仿真值结果显示:在烘箱的底层,温度最高,随着高度增加,温度值趋近相同;测试值结果显示烘箱中上层的温度趋近相同,但是底层温度最低。
通过上述分析,可以看出仿真结果与试验结果在空间上的差异不大,差异主要体现在沿着烘箱高度方向,仿真值显示底层温度最高而试验结果相反,但是随着高度的增加,烘箱的温度值趋近相同,并且试验值和仿真结果接近。
2.3.2 不同设定温度下试验结果的分析
在设定温度为50 ℃时,将40 支温度传感器采集的温度数据去除误差后,得到烘箱内部所有测试点温度分布情况,筛选两个控温区中的温度最大值和最小值,如表1 所示。
这4 支传感器的测试值覆盖了烘箱整体温度的最大值和最小值,为了便于观察其内部温度场的整体分布情况,本文绘制了编号为1#、2#、16#、13#、27#、34#的6 支传感器温度随时间变化曲线。由于1#和2#传感器在试验全过程内温度变化非常一致且与控制系统的跟随性较好,为清楚分析二者差异,特截取温度容差范围下限(45 ℃)开始的数据绘制曲线,如图13 所示。编号为16#、13#、27#、34#的四支传感器在试验全过程时间内的温度变化情况如图14 所示。
从图13 可以看出,编号1#和2#这两支位于控制点的测试传感器温度值在达到稳定状态后的30 min内(50~80 min),基本维持在50 ℃左右,最大波动不超过0.5 ℃。说明控温传感器的位置处于整体温度中值,利于整体温度均匀性分布,并且波动性很小,利于整体温度稳定性,控制传感器的位置选定非常合理。从图14 与表1 中可以看出,控温1 区温度和控温2 区的温度与设定值偏离很小,最大偏离量为1.8 ℃,为容差(±5 ℃)的36%;并且两控制区对应的最大值与最小值的差值甚至未超出容差带的30%;另一方面,控制1 区与控制2 区的最大值相差几乎为零,最小值相差仅为0.6 ℃,且从测试点13#、16#、27#、34#在稳定阶段的平均值和方差值也说明了烘箱内部温度均匀性较好。
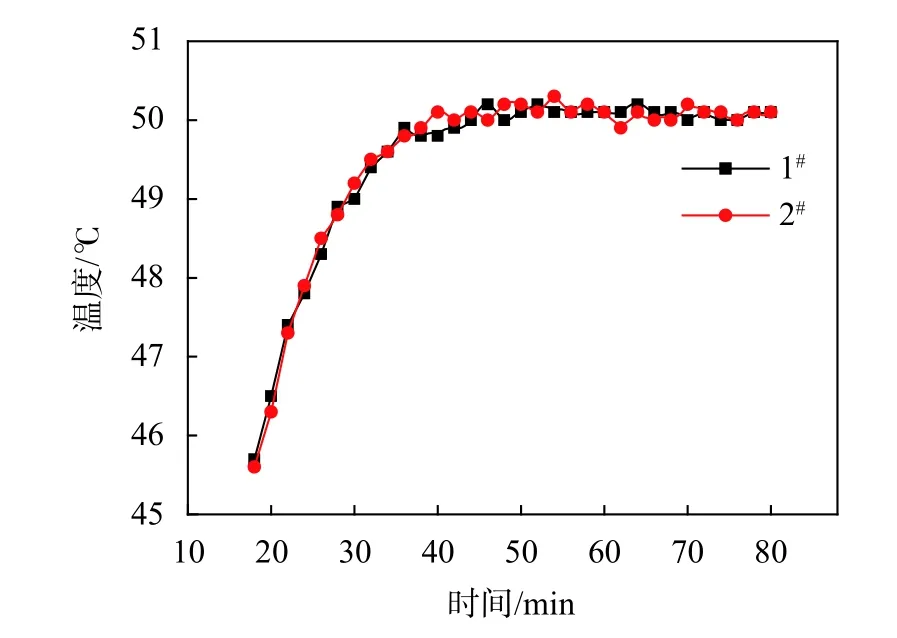
图13 50 ℃控制点传感器温度随时间变化曲线
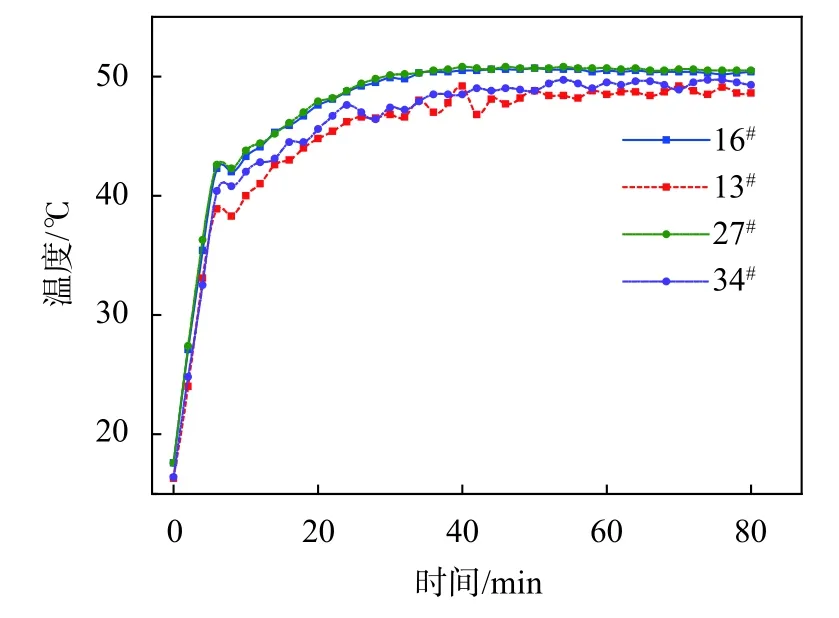
图14 50 ℃两控制区内极值点温度变化曲线

表1 设定值50 ℃温度均匀性测试温度值
为了验证本文所述仿真方法的合理性,保持所有试验条件不变,设定试验温度为85 ℃,对稳定状态下的40 支温度传感器所采集的实时温度数据去除误差处理后,筛选两个控温区中的温度最大值和最小值,如表2 所示。控制1 区和控制2 区的温度最值点所对应的测试传感器分别为16#、13#和27#、25#,绘制编号为1#、2#、16#、13#、27#、25#的6 支传感器温度随时间变化曲线,如图15 和图16 所示。

图16 85 ℃两控制区内极值点温度变化曲线

表2 设定值85 ℃温度均匀性测试温度值

图15 85 ℃控制点传感器温度随时间变化曲线
从表2 和图15 可以看出,编号1#和2#温度值在达到稳定状态后的30 min 内,基本在85 ℃,最大波动不超过0.5 ℃,与50 ℃时的实验情况几乎一致,体现了不同温度下的复现,进一步验证了控制传感器的位置选定是非常合理的。此外,就整体均匀性而言,在烘箱稳定后,13#测试点的温度曲线与设定点85 ℃差值最大,最大偏离量为2.8 ℃,为容差(±5 ℃)的56%;烘箱有效加热区内最大值与最小值的差值为4.3 ℃,占容差带(±10 ℃)的43%,整体波动较小,具有良好的温度均匀性。
3 结束语
1)本文构建了适用于航空大型烘箱的温度场仿真模型,根据烘箱内部的热分布仿真结果,对仅依靠工程经验确定控制传感器位置的传统方法进行了改进,为控制传感器的合理布置提供科学依据。
2)本文以一台航空零件制造用烘箱为实验对象,在其极限使用温度范围处进行了温度均匀性测试,并将试验结果与仿真结果在空间上的差异性进行了比较分析。此外,通过温度测试数据分析,烘箱整体的温度均匀性分布较好,在不同设定条件下有良好复现性,有效工作区内温度值与设定值最大偏离量不超过容差的56%,最大值与最小值的最大差值占容差带的43%,证明了利用温度场仿真分析手段确定控制传感器位置,从而提高设备温度性能的方法有效。
3)在后续研究中,可根据烘箱底部实际材料进行边界条件的精确限制,对仿真模型进行优化。更进一步地,可以考虑将该方法应用于装载情况下的大型烘箱温度场模拟,为零件在烘箱中的合理布置提供分析手段。

