一种智能车图像采集减振平台设计与仿真分析

邵泽鹏，罗建南，喻 凡

（1.上海交通大学 智能汽车研究所，上海200240；2.上海大学 机电工程与自动化学院，上海200444）

作为智能汽车感知融合中的重要组成部分，图像信息采集平台的稳定性对图像采集工作的效果是至关重要的。目前，随着智能汽车发展与增长，车载精密传感器的隔振抑振提出了新需求，为了监视路面情况与行驶记录，在一些公共安全车辆车顶搭载了图像信息采集装置。为了更精确地定位路障信息，记录路面情况，智能图像信息采集平台对车载隔振抑振系统更精准的低频振动抑制能力提出了更高的要求，用Stewart平台进行隔振抑振能很好地解决这一实际问题。

Stewart 平台是一种由6 条相同支链并联组成的，位姿可控的多自由度平台，与传统的串联机构相比具有输出精度高、结构刚性好、承载能力强、便于控制等优点，在实际应用中与串联机构互补，实现空间6自由度隔振。其隔振效果好、工业应用广泛，成为国内外机构学学者的研究热点。

1965年德国学者Gough Stewart[1]首次提出Stewart平台的设计后，后来学者们将其称为Stewart平台，现已在工业上被广泛应用[2]。如直升机隔振设计中，通过在旋翼与机身间连接处的Stewart减振平台对顶部旋翼的振动进行隔离与抑制，降低直升机机身的振动，增强行驶稳定性[3]，吴兆景等[4]提出的一种引入磁流变半主动控制技术和立方结构Stewart 平台的直升机主减隔振平台能够有效抑制某型直升机旋翼/主减系统1 阶通过频率23.9 Hz 的振动载荷向机身的传递。在微创手术中，由于机器人操作通道小，对机构空间性能与输出精度有很高要求，Stewart 平台由于具备精确位姿调整的能力，被广泛应用到微创手术机器人设计中[5]。在大型舱段装配的中应用的装配机器人，传统上多为串联机械臂，由于串联机构关节较多，这类机器人作业范围大，避障能力强，但其末端执行机构承载能力弱，结构变形大，装配精度难以承担重载精密零部件装配的要求。面向高精度、高复杂度的航空器舱段装配，通过并联6 自由度机构装配是一项新兴的技术[6]。除此之外，Stewart平台还在高精度卫星与载荷间隔振[7-8]，海上廊桥隔振抑振[9]，足踝仿生复合体[10]，风洞实验位姿调节系统[11]等领域广泛应用，用于满足调节系统高精度、可控性好、解耦性好的要求。综上，Stewart 平台已经广泛应用于大型机构的隔振抑振系统中，但在智能车车载精密位姿控制与隔振系统中研究应用有限。在Stewart 平台已有应用领域的隔振抑振系统中，为了实现对高频振动优秀的隔离能力，往往忽略了对低频振动抑制能力，不能满足对低频振动敏感的智能车载信息采集系统的对低频振动抑制的需求。

Stewart 平台由于其动力学模型复杂且运动学正解较难得到，在实际应用设计中仍以数学分析辅助多体软件仿真为主。焦健等[12]运用ADAMS构建物理样机并在Simulink 中建立了控制系统模型，验证了Stewart平台的良好隔振性。ADAMS软件能够较好的处理非理想状态下的非线性响应，故针对某智能车用图像信息采集平台对姿态可控的设计要求，本文基于ADAMS 仿真环境研究设计了一种结合减振惯容器的Stewart平台虚拟模型，并验证了模型的准确性。仿真结果表明，Stewart并联平台对于复杂路面振动经过车辆悬架系统抑振后的中低频率振动的抑制作用效果明显。

1 平台构型与动力学模型

1.1 平台构型

Stewart 平台由上、下两个平台以及6 只相同的支腿构成。每个支腿上搭载一个滑动副，并加装弹簧-阻尼结构，在上下两端通过虎克铰或球铰与上、下两个平台相连接，构成完整的6自由度平台。

如图1 所示。机构的上平台为动平台，下平台为静平台，通过6 只支腿的长度变化以影响和控制上平台的位置和姿态，包括3个方向上的平移与3个方向上的旋转共计6个自由度。

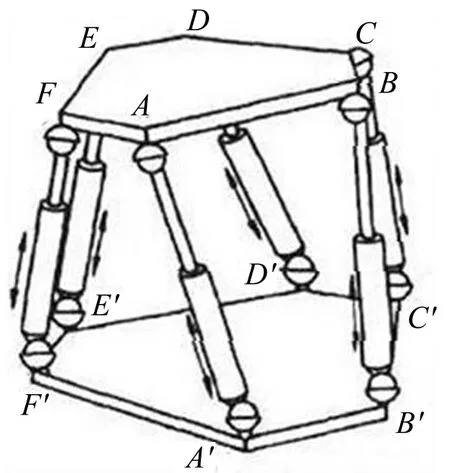
图1 Stewart平台CAD模型图

1.2 动力学模型建立及其特性分析

为Stewart 建立力学模型的常用方法包括Newton-Euler 法、Lagrange 法和Kane 法等。位姿受到控制的上平台接受6 只支腿的作用力、自身重力和平台上承载的外力。采用Newton-Euler法对运动的上平台列出动力学方程为：

式中：Fi为支腿对上平台的作用力，ri为各支腿与上平台作用点相对于上平台质心的距离矢量，F0、M0为上平台受到载荷的的外部作用力、外部力矩。

在实际的工程抑振隔振中，固有频率是决定系统振动特性的主要物理特征，是在模型设计中避免路面输入与隔振系统产生共振的重要依据。相较于Stewart在其他领域的用法，为了防止抖动造成的成像模糊，车载相机对低频振动更敏感，车载相机对隔振系统在低频区的隔振表现要求更高。需要降低隔振系统的固有频率，远离经车辆悬架系统过滤后的输入的主要激扰频率。车载隔振系统的设计要在这一原则的指导下进行系统固有频率的调节。

系统固有频率只与系统自身属性有关，在去掉外界振动激励与外部作用力后，忽略6 只支腿相较于平台较小的质量，将支腿模拟成弹簧-阻尼单元，可以得到系统的自由振动方程为

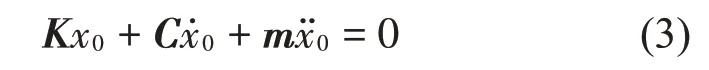
弹簧-阻尼系统的共振频率ω0由无阻尼固有频率ωn与系统阻尼比ζ共同决定：

无阻尼固有频率ωn和系统阻尼比ζ可由下式求得：

结合上述式（4）至式（6）可知，系统的共振频率与上平台位姿、系统结构参数K、C、m有关：

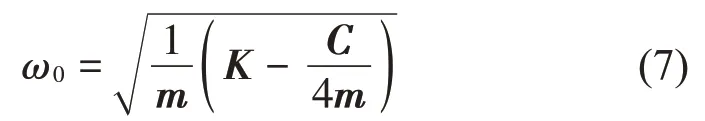
针对这些参数，可以通过ADAMS 中调节模型参数以验证系统结构参数对系统共振频率的影响，并找到具备良好低频隔振效果的参数组。

2 模型与试验设计

基于式(7)，为验证系统共振频率与系统参数的定性关系，寻求在给定条件下可将系统共振频率控制在要求范围以内的系统结构参数组，通过在ADAMS环境中，在设计约束条件下进行仿真，检验所设计Stewart 平台对车辆输入低频振动的抑制效果，寻求结构参数对系统共振频率的影响规律，以及试验通过惯容器等元件优化系统性能的可行性。

2.1 模型设计与约束

根据车载摄像平台所处环境的设计要求，在Solidworks 中进行三维建模以及模型的装配与调整，三维模型图如图2所示。模型由有3条支板的Y型上下平台，各6 只上、下支腿以及连接件组成，重要尺寸参数如表1所示。在支腿完全拉伸的初始状态下，Stewart上下平台的俯视图如图3所示。

表1 三维模型中重要尺寸参数表

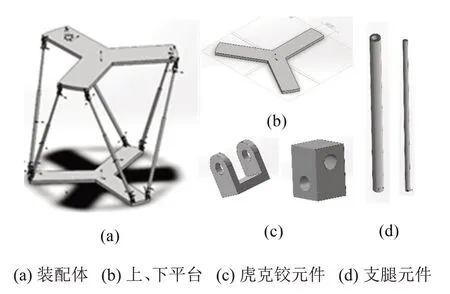
图2 Stewart平台装配与重要元件

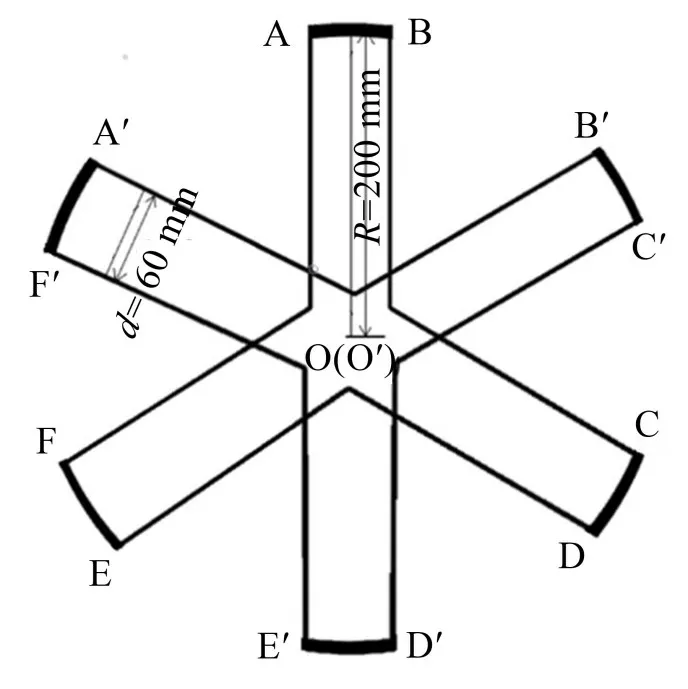
图3 Stewart平台模型上下平台俯视图

则可知在支腿完全拉伸的初始状态，平台高度H可由下式得出：

将模型导入ADAMS 中进行仿真，在几何模型基础上添加连接与力。整体元件与约束清单如表2所示。

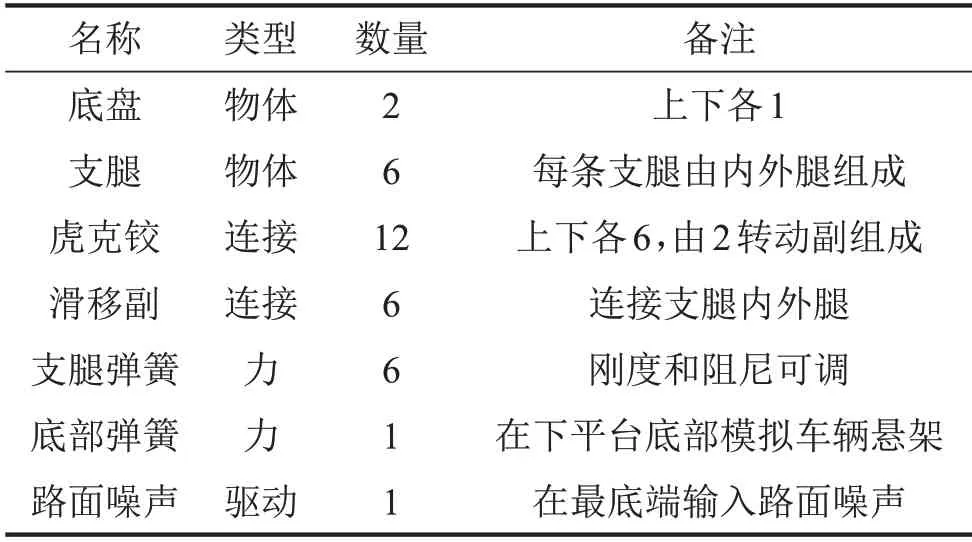
表2 ADAMS模型中主要物体、连接与力清单

在ADAMS 中建立好的Stewart平台模型如图4所示，其中覆盖在支腿上与模型底部的螺旋线圈为刚度、阻尼可调的弹簧。

图4 ADAMS环境下搭建的Stewart平台模型图

2.2 试验条件参数设置

根据式（7）中的共振频率公式，结合实际中对装置质量、行程、刚度等对平台参数的要求，设定平台具体参数的取值范围，并通过仿真分析关键参数对共振频率的影响效果。试验仿真参数设置如表3所示。其中上平台质量由平台搭载的相机系统决定，支腿弹簧刚度由最大行程和第一模态频率限制。

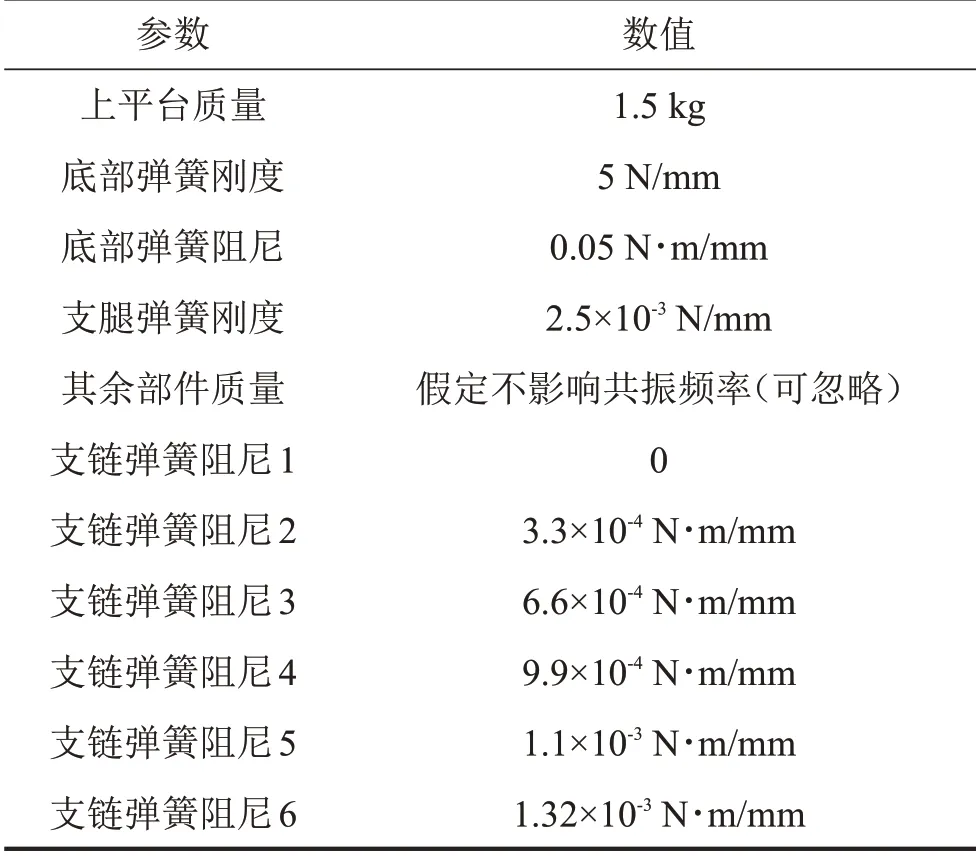
表3 仿真试验关键参数表

根据如图5 所示的一典型路面不平度实测曲线[13]，在车速20 m/s 的条件下，进行傅立叶变换，得到的路面不平度速度功率谱密度主要集中在1 Hz～100 Hz 中。在此基础上于MATLAB 中生成采样频率为100，频率在1 Hz～100 Hz 之内的10 秒钟路面激励速度白噪声用于模仿路面输入。生成的路面速度白噪声与通过积分得来的路面噪声位移如图6所示。

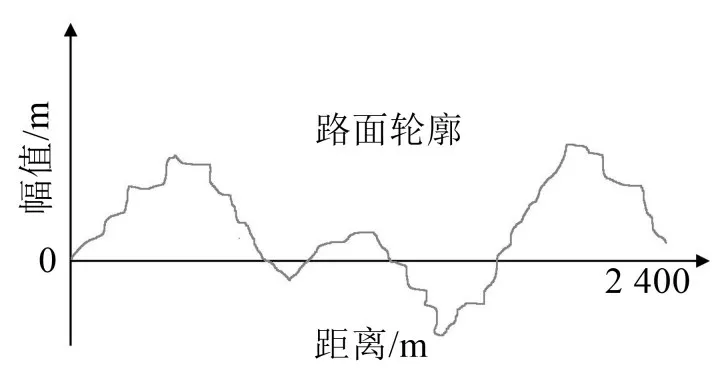
图5 一典型路面的实测路面轮廓

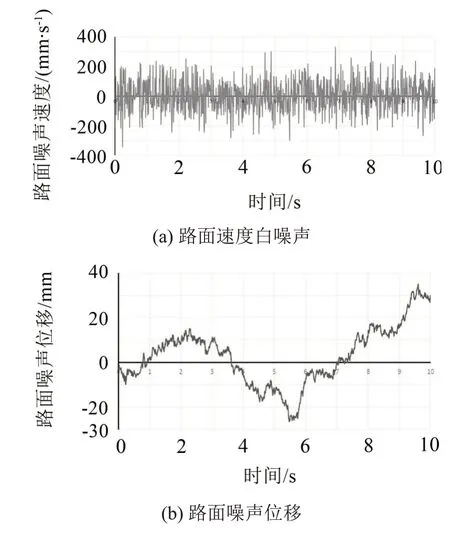
图6 用于仿真的路面输入

3 仿真结果分析

为方便探究结构参数对系统振动特性的影响并找到合适的结构参数，控制Stewart平台下平台输入激励与上平台的运动均在竖直方向上进行。在这种情况下系统的振动简化为两个模态，为了增强系统在低频区间的抑制作用，需要控制共振频率较低的系统模态，将其共振频率控制在约0.5 Hz以内。

3.1 不同阻尼比下系统不同模态的共振频率与频域响应

通过改变阻尼，进行多组仿真试验，比较在不同的阻尼比情况下，系统的共振频率与频域响应曲线。得到的系统各模态的共振频率如表4所示。频域响应曲线如图7所示，时域响应曲线如图8所示。

图8 不同阻尼比下系统时域响应曲线

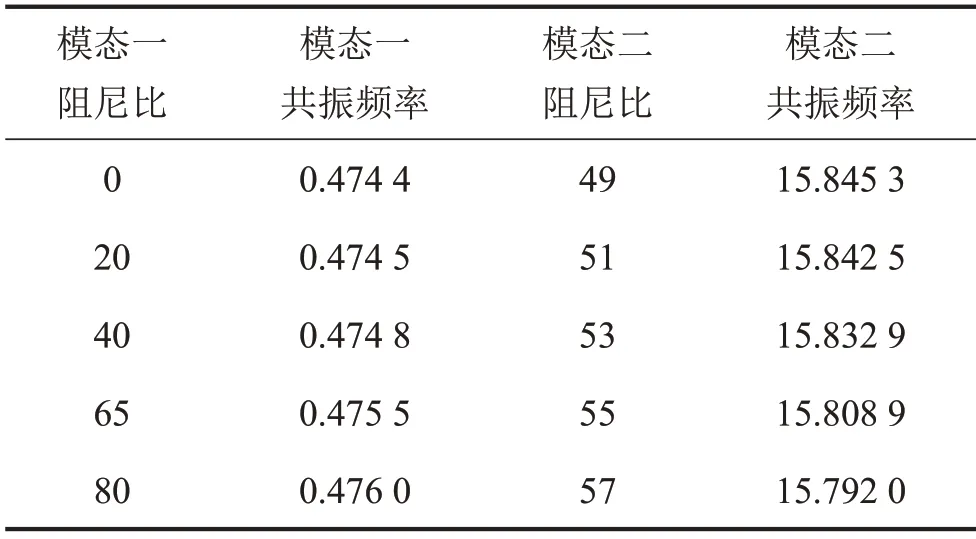
表4 不同阻尼比下系统共振频率

图7 不同阻尼比下系统幅频特性比较

分析共振频率接近低频区间的模态一，发现随着阻尼升高，其共振频率略有升高，而共振的强度则迅速下降，同时对1 Hz～10 Hz的激励的抑制效果有轻微削弱。在阻尼比65%的情况下较好地规避了共振区间的同时，保证了对1 Hz～10 Hz的激励的抑制效果。在时域响应中，随着阻尼比的增长，位移曲线更光滑，抖动更小。

3.2 结构参数对系统频域特性的影响

在已有模型上调整若干结构参数，整理对低频振动频率大小和高频激励抑制效果的影响，效果如表5。

表5 结构参数对系统频域特性影响分析

4 引入惯容器优化减振效果

虽然增加上平台质量能够降低模态一的固有频率，但在实际的工程应用中过高的质量会增加平台与车辆的负担。可以采用Smith[14]在2002年提出的惯容器进行减振，利用其可以通过较小实际质量代替较大惯性质量，对低频区间激励抑制效果强的效果，对减振效果进行进一步优化。体积轻便、便于使用在车辆减振系统中的惯容器的机械实现方式主要包括齿轮齿条惯容器、滚珠丝杠惯容器等[15]，已经被研究应用于汽车被动悬架[16]、剪式座椅悬架[17]、铁路车辆垂向振动抑制[18]等领域中。

本文在ADAMS 仿真试验中通过在支腿与Stewart平台的上平台或下平台相接处铰接飞轮，通过耦合副将上下支腿的相对运动与飞轮旋转联系起来，如图10 所示。则惯容器的等效质量meq可由下式给出：

式中：J为飞轮惯量，rgear为飞轮半径。由式(9)可知，飞轮半径越小，惯容器等效质量越大，共振频率越低，越能使共振频率远离系统输入的激励频率。

惯容器可以加装于上平台或者下平台。在上平台或下平台增加惯容器后，该减振系统的传递函数可分别由下式(10)、式(11)给出：

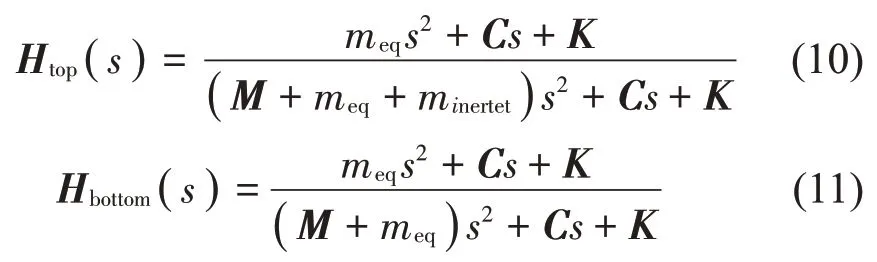
在MATLAB 中依据系统参数，画出式(10)、式(11)中传递函数的Bode图，如图9所示。

图9 传递函数在MATLAB中的Bode图

分析式(10)、式(11)可以得出：

(2)对于抑振区间，加入惯容器后抑振效果得到增强；

(3)在重点关注的0～10 Hz范围内，加入惯容器后的隔振平台对路面振动的抑制作用普遍优于加入惯容器之前；

(4)比较惯容器装在上、下平台的幅频曲线，发现曲线特征相近，但在高频区的稳定幅值略有差别。这是惯容器本身质量带来的影响，装于上平台时相当于增加了上平台的簧上质量。

在Stewart平台的初始条件下，与在上平台或下平台加惯容器，或缩小下平台飞轮半径相比较，得到的系统频域响应图如图10所示。在ADAMS中的仿真结果图与MATLAB中传递函数的结果一致。

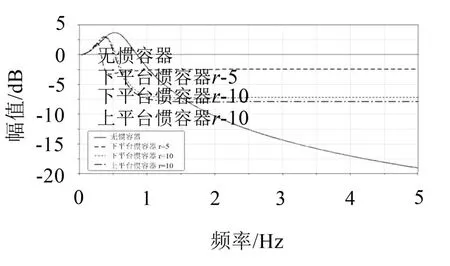
图10 不同惯容器对系统频域响应曲线的影响

结合系统条件限制分析后，当单个飞轮J=17×10-4kg/(m2)，rgear=10 mm 时，单个惯容器等效质量为1.7 kg。可以用较小的质量等效较大的上平台载荷，能够较好优化系统特性。

5 结语

利用基于弹簧-阻尼系统的Stewart 隔振平台，能够在车辆悬架系统减振后较好地进一步抑制低频振动激励，有助于车载摄像头减振防抖。

上平台质量与系统共振频率负相关，支腿的弹簧刚度与阻尼与系统低共振频率正相关。通过调节振动相关系统参数可以将共振频率降至0.5 Hz 以内，能较好地抑制悬架减振后在1 Hz～10 Hz区间的振动。

实际应用中上平台的质量受负载和振幅限制，为了用更小的质量实现更低的共振频率，可以通过在支腿上加装惯性子以进一步优化系统整体性能，减轻重量，降低共振频率。