单轮对多功能试验台液压激振伺服系统的控制设计

肖 乾，杨丽婷，周生通，郭维年，周新建

（华东交通大学 机电与车辆工程学院，南昌330013）

随着我国高速铁路的迅速发展，高速动车组作为高铁系统的核心装备，其轮轨关系将会影响高速列车的最高运行速度、车轮镟修周期和高速铁路的服役安全性[1]，因此对其动力学性能的研究，特别是关于轮轨关系的研究，一直是世界高速列车研究的重要课题。目前，国内学者大部分通过现场实测或通过软件模拟的方式研究轮轨力、轮轨噪声、钢轨波磨特性等对轮轨关系动力学的影响[2-4]，取得了较好的研究成果，但通过现场实测的方式较为繁琐且不便捷，为克服这一难题，本文介绍一种主要用于动车组轮轨关系试验和轮轨作用机理研究的新型设备－单轮对多功能试验台，它通过高速调频电机带动车轮和钢轨轮的对滚，达到仿真并测定其疲劳条件下的各种试验数据，模拟车轮与轨道滚动摩擦磨损、滚动接触疲劳、一系悬挂可靠性以及接触振动等试验；其中，液压激振伺服系统是试验台的关键部分，它必须具备模拟高速动车组轮对在不同工况下轨道不平顺引起的振动与冲击的功能，对液压激振伺服系统的跟随性、响应时间和系统鲁棒性等动态特性提出了更高的要求；因此，开展单轮对多功能试验台液压激振伺服系统性能的研究具有重要科学研究意义和工程应用价值。

液压激振技术按激振方式原理可以分为直流液压激振技术、交流液压激振技术、液压射流激振技术和电液伺服激振技术[5]。Ruan 等[6]介绍了一种利用单阀芯的旋转运动和直线运动的独特的先导控制阀，可大幅度提高激振频率。郝建功等[7]结合电气与液压传动的性能优势,开发出电液激振装置,推导出该装置相关参数的相互关系式。肖乾[8]等研究液压减振器主要结构参数，利用建立的模型通过数字试验全面分析各结构参数对阻尼特性的影响；毛阳等[9]基于武钢一热轧步进梁工作中出现设备老化等问题，从原系统的工作原理入手，运用模糊PID对系统进行控制，解决了步进梁在工作中的问题。石天飞等[10]在LNG储罐穹顶液压整体提升技术中，运用模糊控制原理，通过建立提升系统仿真模型，有效改善提升过程的不平稳性。李文华等[11]伺服电机驱动内啮合齿轮泵为基础，通过Simulink 软件建立系统仿真模型，解决了节能液压泵站控制系统效率不高和抗干扰性差的问题。Wei[12]通过建立管道和激波器组成的液压激振伺服系统，经过控制变频器的变频调速，对管道不同点处的振动信号进行了采集和分析，研究并得出了液压管道的振动控制规律。Ren等[13]设计了一种以谐振方式运行的高频电液激励系统，从水力共振的基本机理、控制方法和共振的利用等方面探讨了水力共振的特点，为高频状态下实现稳态大液压激振力研究奠定了基础。

从已发表的文献来看，国内外学者对液压激振伺服系统已有一定的研究，并取得了较好的研究成果，但大部分都是基于液压系统伺服阀控制参数进行研究，针对液压激振伺服系统的控制参数、结构优化和动态性能进行全面分析的研究成果较少，特别是针对单轮对多功能试验台的液压激振伺服系统的研究成果尚未见诸报道。本文通过建立单轮对多功能试验台液压激振伺服控制系统数学模型，选取液压元件的主要结构参数，在Simulink 中采用自适应模糊PID的控制策略对单轮对多功能试验台液压激振伺服控制系统的控制方式进行优化，并通过Simulink 和AMESim 的联合仿真技术，将Simulink中经过自适应模糊PID 控制策略处理后的信号，作为AMESim中建立的单轮对多功能试验台液压激振伺服系统模型的输入信号，实现单轮对多功能试验台液压激振伺服控制系统的动态性能研究，为液压激振伺服控制系统设计提供依据。

1 系统的液压原理和数学模型的建立

图1所示为单轮对多功能试验台，主要由台架、驱动装置、模拟轮和液压激振伺服系统组成，其中液压激振伺服系统是关键。液压激振伺服控制系统由液压缸、液压泵、伺服阀、连接管路及其他元件构成，液压激振伺服系统液压原理图如图2所示。

图1 单轮对多功能试验台

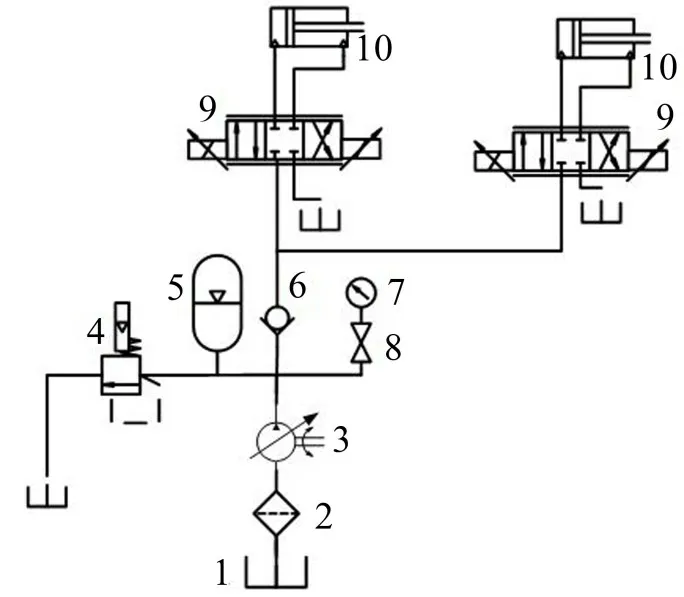
图2 液压激振伺服系统原理图

单轮对多功能试验台液压激振伺服系统以惯性负载为主，采用电液力伺服控制，液压激振伺服系统正常工作时，给定伺服阀指令电压，伺服阀将指令电压和系统反馈电压相比较，得出偏差电压信号并进行相应的放大，阀芯随之进行快速换向，带动液压缸作往复运动，达到液压激振的效果；其中，当系统管道内的流体压力大于管道额定压力时，将系统管道内的流体通过溢流阀卸荷到液压缸中，保持系统的压力稳定，防止出现管道爆裂等事故的发生；蓄能器在系统运行过程中能够存储能量、起到吸收液压冲击和消除脉动的作用。

根据液压激振伺服控制的液压原理图，建立液压系统数学模型，对液压系统的动态特性进行研究。

液压缸流量连续性方程[14]：

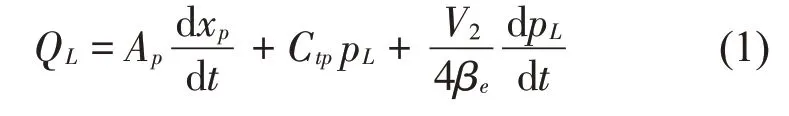
式中：QL为负载流量，Ap为活塞缸的有效面积，xp为活塞位移，βe为液压缸有效体积弹性模量，pL为负载压力，V2为液压缸回油腔的容积，Ctp为液压缸的总泄漏系数。

伺服阀是零开口四边滑阀，供油压力ps恒定，回油压力p0为零，伺服阀的线性化流量方程为：

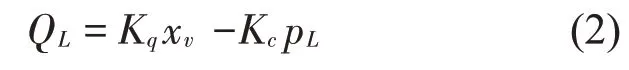
式中：Kq为系统流量增益，xv为阀芯位移，Kc为流量压力系数。

液压缸的输出力和负载力的平衡方程为：

式中：mt为活塞的总质量；Bp为活塞及负载的黏性阻尼系数；K为负载弹簧刚度；FL为作用在活塞上的任意外负载力；Fg为液压缸输出力。

将上述的伺服阀控液压缸的基本方程式(1)、式(2)、式(3)的拉普拉斯变换为：

将式(4)简化，得到流量Q至液压缸输出力的传递函数。

系统的开环传递函数为：

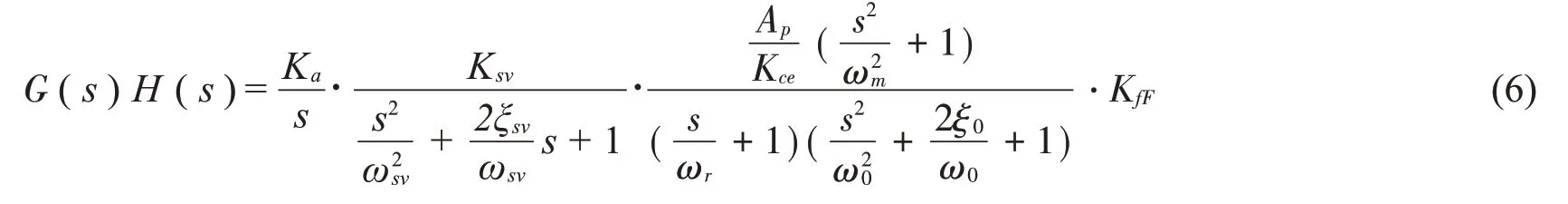
式中：Ka为伺服放大器的增益；Ksv为液压阀的伺服增益；ξsv为伺服阀阻尼比；ωsv为伺服阀的固有频率；ωr为液压缸的液压弹簧与阻尼系数之比；ω0为液压缸的液压弹簧与负载的固有频率；ξ0为液压缸的阻尼比；Ksv为系统总流量压力系数。

2 Similink模型建模与仿真

2.1 建立simulink模型

本节以单轮对多功能试验台液压激振台为例，基于方程式(6)得出系统是由伺服放大器的1阶积分环节、伺服阀的2 阶振荡环节和液压缸的传递函数组成；因此，通过方程式(6)在Simulink软件中建立控制模型。采用ODE45算法求解，得到液压激振伺服系统的稳态响应，计算中采用的液压激振伺服系统仿真参数和液压激振伺服控制系统的仿真模型如表1和图3所示：

表1 仿真参数

图3 液压激振伺服控制系统的仿真模型

液压激振伺服控制系统在输入为阶跃和正弦信号下的响应曲线如图4和图5所示。

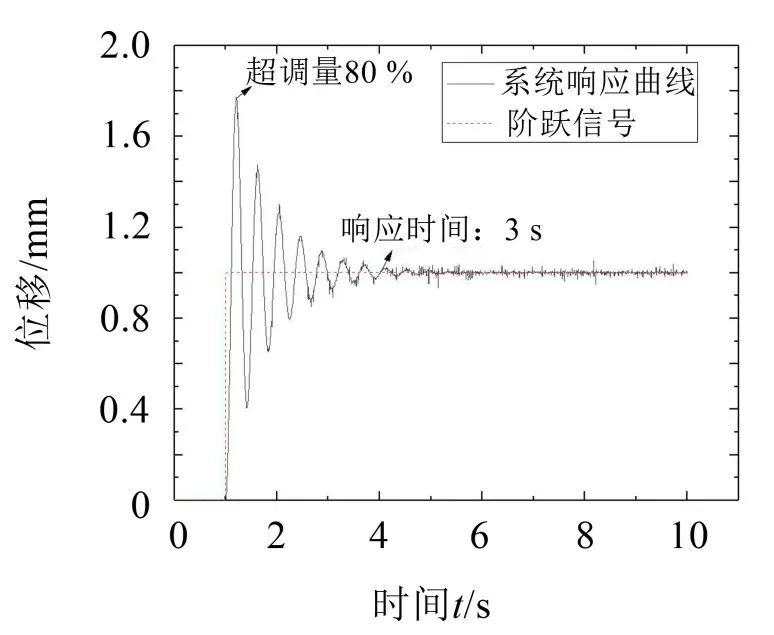
图4 系统阶跃响应曲线

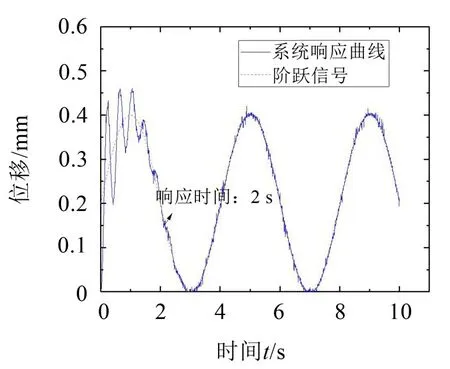
图5 系统正弦响应曲线

2.2 模糊PID控制器的基本原理

模糊PID控制算法适用于不确定因素较多的系统，能根据系统的偏差和偏差变化率将模糊控制器分别进行模糊化，模糊逻辑推理，解模糊化等操作，最后做出最优控制参数的选择，模糊PID 控制结构原理和基于自适应模糊PID控制的液压系统仿真模型如图6和图7所示。

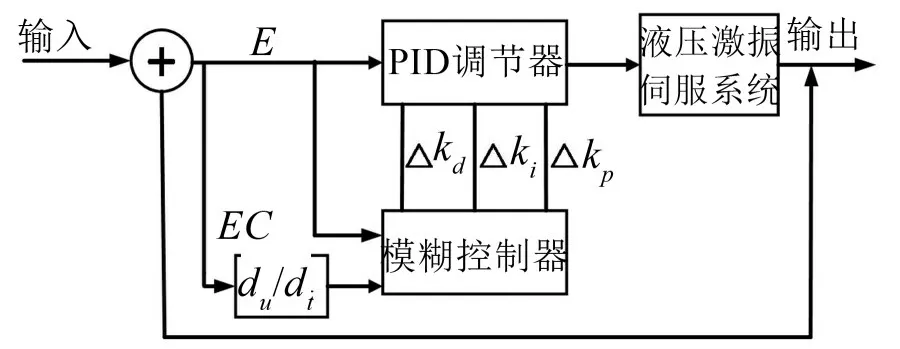
图6 自适应模糊PID控制器结构

图7 基于自适应模糊PID控制的液压系统仿真模型

2.3 隶属度函数

本文所述的液压激振伺服系统模糊控制器拟采用二输入三输出的形式，自适应模糊PID 控制规则如表2 所示：以偏差e和偏差变化率ec作为输入变量，Kp、Ki和Kd为输出变量，E和EC的模糊论域量化为[-1，1]，Kp模糊论域为[-1，1]，Ki和Kd的论域取值为[-0.5,0.5]。

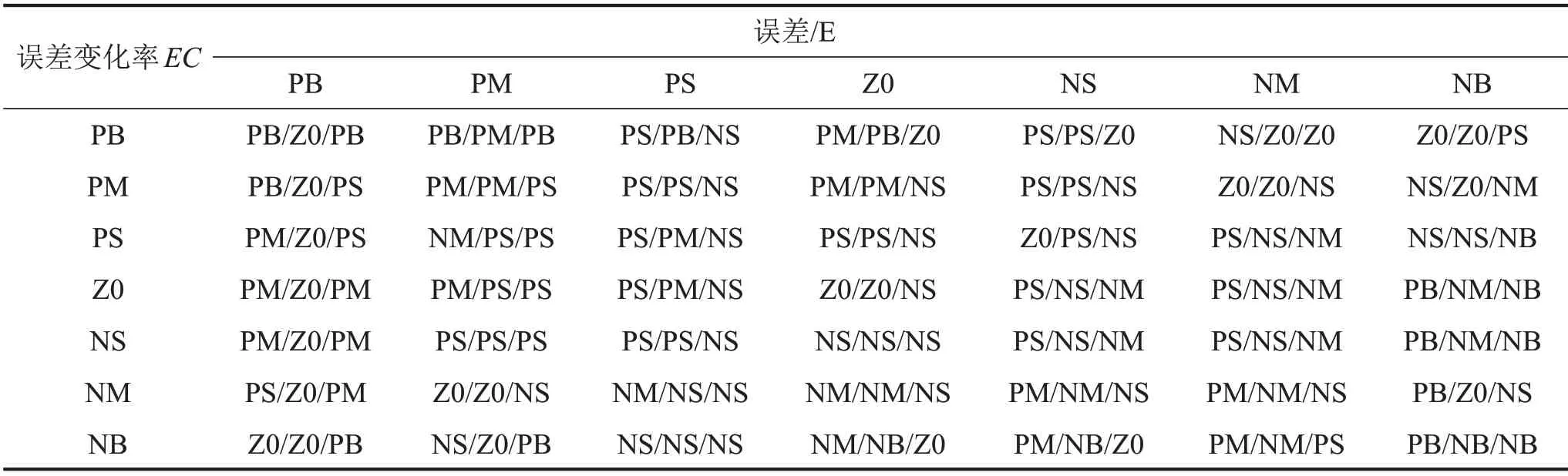
表2 自适应模糊PID控制规则表

2.4 模糊PID模型建模仿真

基于Simulink软件的模糊控制器建模环境，采用重心平均的去模糊化方法，建立单轮对多功能试验台液压激振伺服系统模糊PID 控制模型，整个模型由模糊控制器模块、PID模块、控制对象及输入输出等部分组成。

观察图4、图5、图8和图9可以看出,采用自适应模糊PID 控制策略后，系统的响应时间误差从原来的2 s 减少为0.5 s，响应速度提升了75%；超调量由原来的80%减小到3%，说明系统输出响应时间和跟随性明显提升，具有较好的鲁棒性，达到了液压激振伺服系统控制优化的效果，能满足系统设计的基本要求。

图8 校正系统阶跃输出响应

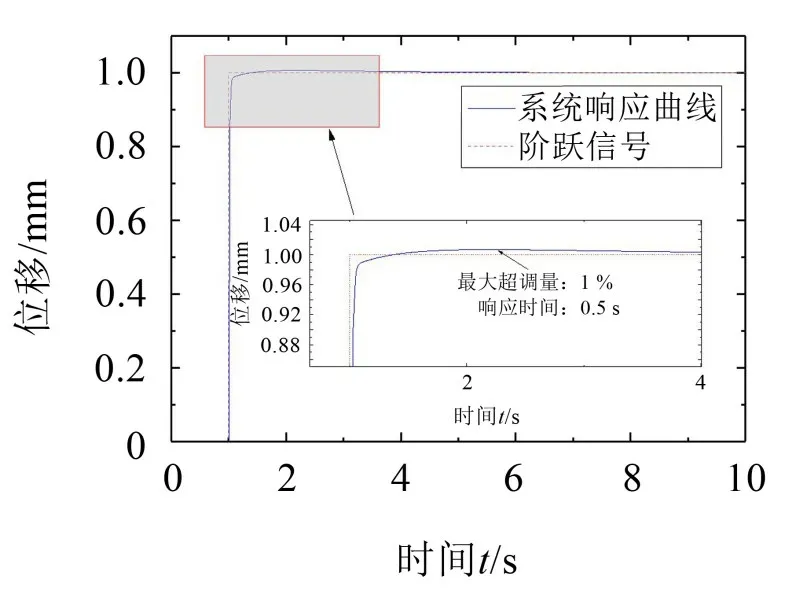
图9 校正系统正弦输出响应

3 Simulink-AMESim联合仿真

本节以单轮对多功能试验台的液压激振伺服系统作为研究对象，将图7的自适应模糊PID控制的液压系统仿真模型作为基础，在AMEsim 和Simulink中分别建立单轮对多功能试验台的激振伺服系统模型和控制协同仿真模型，如图10 和图11 所示；联合仿真接口模块，实现实时的联合仿真。通过Simulink 与AMESim 联合仿真，将正弦信号作为系统的原始输入，分别研究负载、流量对液压激振伺服系统控制效果的影响。

图10 基于AMESim的系统仿真模型

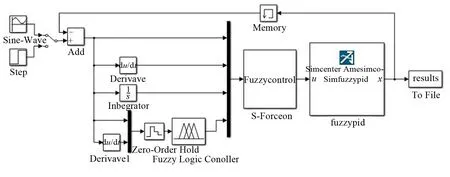
图11 基于Simulink和AMESim的自适应模糊PID控制协同仿真模型

（1）研究不同负载（不同车型的轮对质量）对系统控制效果的影响的影响。

不同车型的轮对质量如表3所示。

表3 不同车型的轮对质量

由图12 可以看出，液压激振伺服系统在以CRH2动车、CRH2拖车、CRH3动车和CRH3拖车的轮对质量为负载，系统的输出响应曲线和以CRH3动车轮对质量为参照的输出响应误差曲线图，可以发现：CRH2 动车、CRH2 拖车、CRH3 拖车的系统输出响应误差最大分别达到了0.011 4 mm、0.011 2 mm和0.011 5 mm，系统输出响应曲线从波峰位置运动至波谷位置的出现了较大的输出响应误差；表明系统的输出位移在液压缸的极限位置（波峰、波谷）出现较大的偏移。

图12 不同负载下的输出响应

为进一步分析系统的输出控制效果，以正弦信号作为标准，采用稳态跟踪误差百分比来对控制器输出的误差的离散程度做定量分析。

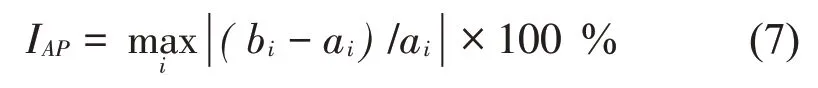
式中：IAP为系统稳态跟踪误差百分比；a(i)为正弦信号输入，b(i)为不同工况在i次采样时的输出。

控制效果评价指标（不同车型）如表4 所示：由表4 可知，CRH2 拖车的IAP最大，其大小达到了18%，CRH2 动车、CRH3 动车和CRH3 拖车的IAP分别为23%、12%、10%；说明随着车体轮对质量的增加，其输出曲线误差会随之增大；因此，在针对不同车型的轮对进行实验时，为保证实验的准确性，应该适当调整伺服系统的油源压力

表4 控制效果评价指标（不同车型）

（2）研究不同流量对系统的控制效果影响。

控制效果评价指标（不同流量）如表5所示。

表5 控制效果评价指标（不同流量）

由图13 和表5 可以看出，液压激振伺服系统在流量为20 L/min、30 L/min和40 L/min下系统的输出响应曲线，可以发现：系统流量为20 L/min下的系统输出位移响应在0 s～1 s 之间呈现一元线性回归方程的曲线特性，同30 L/min、40 L/min情况下的流量输出曲线相比出现较大的失真现象，IAP的大小达到了35%，远远大于30 L/min和40 L/min的IAP；同时，发现系统在2 s～10 s内，误差也相应出现一些波动,但是从整体来看输出曲线实现了稳定的输出，说明系统在启动的瞬间，输入流量的大小会对系统的输出效果产生较大的影响。

图13 不同流量下的输出响应

4 试验研究

试验基于单轮对多功能试验台，采用模糊自适应PID控制算法，驱动液压伺服系统硬件，试验硬件为研华科技的610L工控机，试验台外观和试验步骤流程如图14和图15所示。

图14 试验台外观图

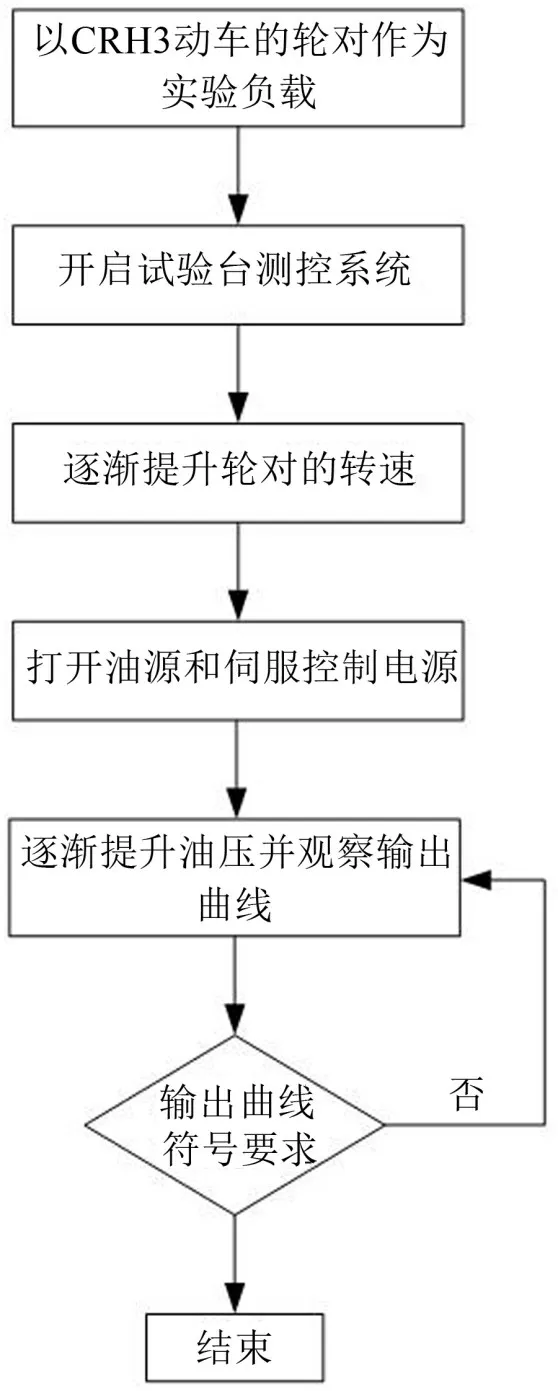
图15 试验步骤流程图

实验以CRH3 动车的轮对质量作为负载，首先将轮对的速度调节到6.0 km/h，然后打开油源和伺服控制电源，逐步提升油源压力至输出曲线基于稳定状态，输出结果如图16所示：可以发现，系统的输出位移同给定的信号相比有大约0.05 s 的时间滞后，输出的位移幅值是给定信号幅值的85%，产生了大约15%的误差，由于试验台在安装过程中会出现一些毫米级的定位误差，在系统实际运行的过程中，轮对的惯性较大，主体结构的误差传递还有液压系统本身结构的误差，会不断累加导致液压激振系统的输出曲线与给定的输入的曲线出现一些误差，但从整体来看，输出曲线呈现了较强的正弦特征，其输出频率、时间周期、波峰和波谷的对称性与给定信号基本相似，考虑到实验情况下会存在较多的外部影响因素，认定此输出位移在可接受的实验误差范围之内；说明本文中采用的自适应模糊PID 算法符满足试验台液压系统的设计要求，可以满足科研项目的实验和相关的测量。

图16 试验结果输出图

5 结语

本文以单轮对多功能试验台的液压激振伺服系统为研究对象，建立了单轮对多功能试验台的液压激振伺服系统的数学模型，设计了自适应模糊PID控制器，利用AMESim/Simulink建立了协同仿真模型，详细讨论外部负载和流量对系统控制效果的影响，并通过试验讨论分析：

（1）采用自适应模糊PID控制策略后，单轮对多功能试验台的液压激振伺服系统，响应时间分别减少了1.5 s，对应的响应速度分别提升了75%，同时超调量减少了77%，说明系统的响应速度、跟随性和鲁棒性得到明显的提升。

（2）研究不同车型轮对作为负载和不同流量作为输入时的系统输出响应，CRH2拖车的IAP最大，其大小达到了18%，说明随着车体轮对质量的增加，输出曲线误差会随之增大；同时发现，输入流量的大小会对系统的启动瞬间产生较大的影响。

（3）以CRH3 动车的轮对质量作为负载进行试验，从整体效果来看，其输出频率、时间周期、波峰和波谷的对称性与给定信号基本相似，说明本文中采用的自适应模糊PID算法符满足试验台液压系统的设计要求，可以用于科研项目的实验和相关的测量。