抛石防波堤地震反应的颗粒流数值模拟

李存柱， 盛 俭， 张鸿斌， 曹苏茜

(1. 江苏煤炭地质物测队， 江苏 南京 210046； 2. 南京工业大学交通运输工程学院， 江苏 南京 210009； 3. 南京水务集团有限公司， 江苏 南京 21000)

0 引言

近年来，国内外人工岛工程屡见不鲜，著名的有迪拜棕榈群岛、日本大阪湾人工岛和伊势湾人工岛、韩国首尔人工岛及中国永暑礁西南岛、美济岛等。历史上关于抛石防波堤破坏的实例屡有报道， 1978年12月和1979年2月葡萄牙悉尼斯港抛石防波堤受风暴引起的波浪影响，其块石护堤发生严重破坏[1]， 1964年美国阿拉斯加发生地震，致使苏尔德和科迪亚克的防波堤严重破坏[2]，抛石防波堤破坏的后果不堪设想，因此保持抛石防波堤稳定的重要性不言而喻。影响抛石防波堤稳定性的主要因素有波浪和地震作用。目前国内外对抛石防波堤稳定性的研究主要基于波浪荷载的影响，对于地震作用下抛石防波堤稳定性的研究相对较少。世界上很多抛石防波堤建造在地震高发地带，并且已有很多抛石防波堤在破坏性地震作用下遭受破坏的工程实例[2-3]。抛石防波堤作为人工岛的主要防护工程，可以防止波浪冲刷，抵挡海浪潮汐，有效地保护人工岛基础设施，减少经济损失和人员伤亡。

目前已有少量关于抛石防波堤在地震动作用下稳定性的研究[3-5]，而部分研究中对于单一级配抛石防波堤地震动力响应的研究相对更少，且地震动输入方式和颗粒粒径对抛石防波堤动力响应的影响尚不明确。此外，抛石防波堤在地震动作用下的变形破坏机制尚不清楚。因此，研究单一级配堆石料的力学性质和变形特征以及抛石防波堤在地震动作用下的动力响应，可以作为工程设计的依据，大大提高设计的准确性，减少因抛石工程失稳引起的人员伤亡及财产损失，且有助于弥补科研空缺，为今后的相关研究提供一定的参考依据。

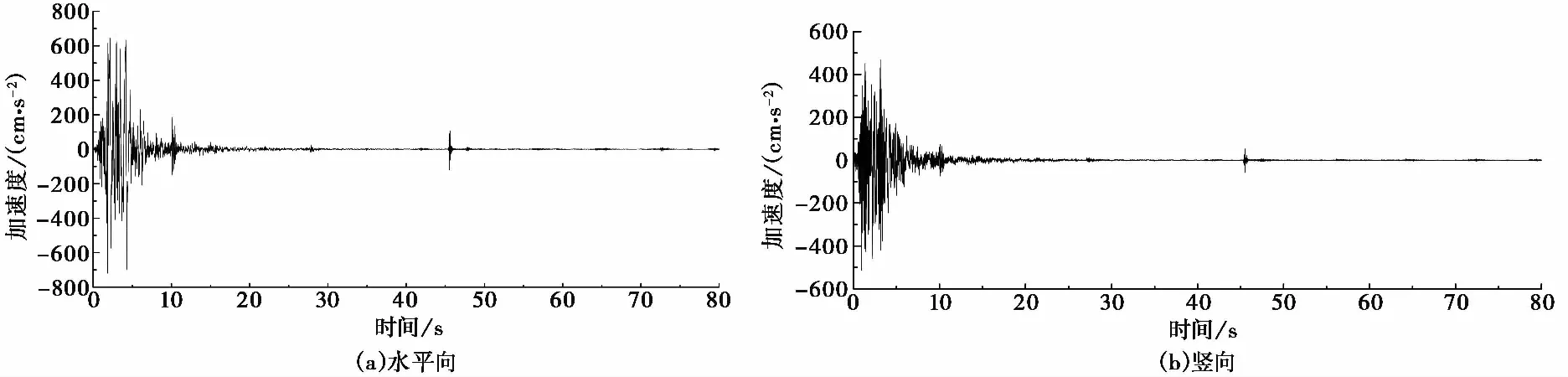
图 1 鲁甸地震加速度时程Fig.1 The acceleration time-history of Ludian earthquake

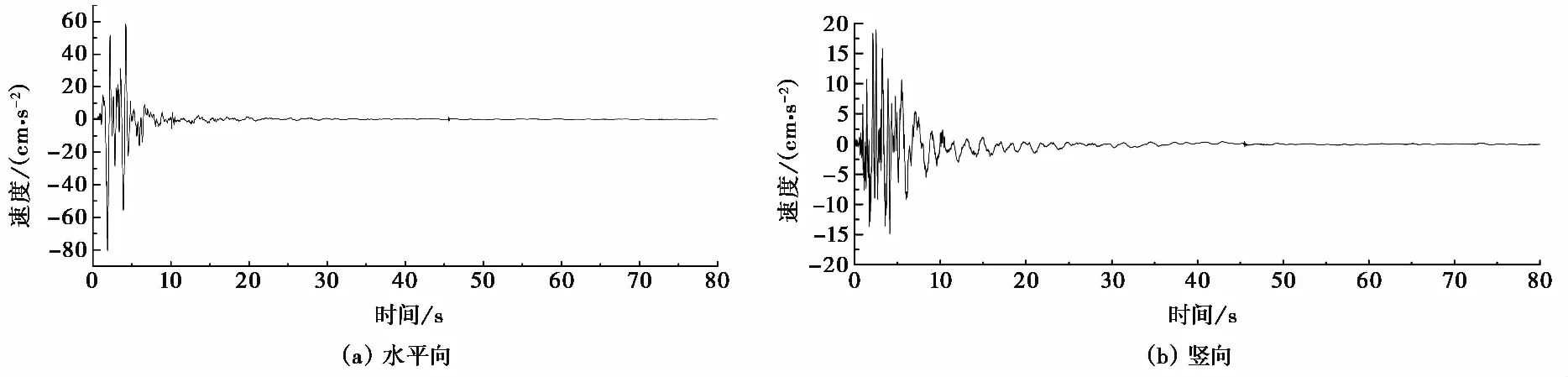
图 2 鲁甸地震速度时程Fig.2 The velocity time-history of Ludian earthquake

颗粒流离散元被广泛应用于岩石材料的相关研究中[6-8]。堆石料为不连续且各向异性的材料，颗粒流离散元刚好可以弥补大型振动台试验和有限元存在的不足，以便探明抛石防波堤在地震动作用下的动力响应以及变形破坏机制。基于PFC2D软件平台，对建造在刚性地基上的抛石防波堤进行数值模拟，鲁甸地区场地为基岩类似刚性地基，所以选取鲁甸地震所记录的加速度时程作为输入地震动，分别分析了抛石防波堤的动力响应受输入加速度峰值、不同输入方式和颗粒粒径大小的影响，以及其变形破坏机制。

1 数值模拟工况与建模

1.1 数值模拟工况

目前抛石防波堤在地震动作用下动力响应的研究主要集中于不同输入峰值加速度对其动力响应的影响[3， 5， 9]，而关于地震动输入方式、单级配堆石料粒径大小对抛石防波堤在地震动作用下动力响应的影响研究较少。本文依据3种不同粒径的颗粒共设计了3组模型，结合输入地震动峰值加速度大小及加载方式确定了36个数值模拟工况。第一组、第二组、第三组数值模型中颗粒平均粒径分别为1.2m、1.6m、2.0m，每一组地震动输入方式为单一水平、单一竖向、水平和竖向组合输入，单一水平输入的峰值加速度分别为0.05g、0.1g、0.2g、0.4g，单一竖向输入的峰值加速度分别为0.035g、0.07g、0.14g、0.28g，水平和竖向组合输入的峰值加速度分别为0.05g和0.035g、0.1g和0.07g、0.2g和0.14g、0.4g和0.28g。通过上述不同工况抛石防波堤动力响应的颗粒流数值模拟，分析不同颗粒粒径、不同输入方式、不同输入峰值加速度对抛石防波堤在地震动作用下动力响应的影响，以及抛石防波堤的变形破坏机制。

1.2 输入地震动

数值模拟中选取鲁甸地震中龙头山镇强震动台站记录的南北向和竖向加速度时程作为水平向和竖向输入地震动，其加速度峰值分别为0.73g和0.52g，图 1为原始的加速度时程曲线。为了考虑不同输入地震动水平的影响，通过调幅，将水平向输入地震动峰值加速度分别调为0.05g、0.1g、0.2g、0.4g，竖向调幅与水平向等比缩小，调幅后的峰值加速度分别为0.035g、0.07g、0.14g、0.28g。

由于PFC的地震动输入只能为速度时程，故需将原始加速度时程经基线校正并一次积分得到速度时程，如图 2所示。

1.3 模型构建

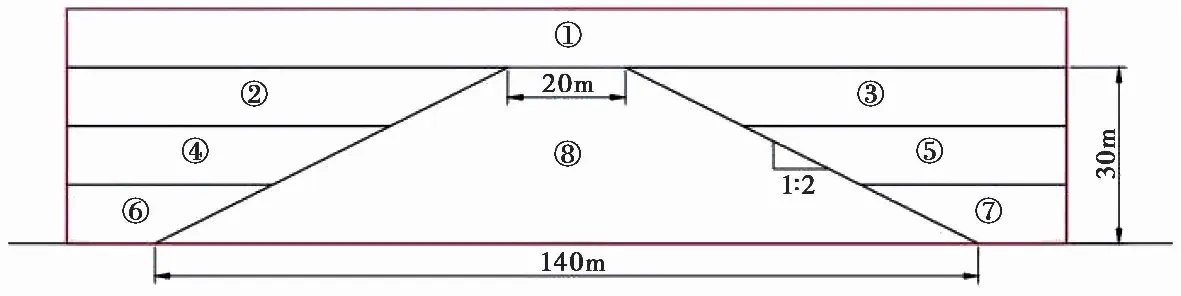
图 3 模型几何示意图Fig.3 The geometric diagram of the model

图 4 初始模型Fig.4 The initial model

参照文献[6]中的几何尺寸，构建了简化且几何相似的抛石防波堤模型。依据抛石防波堤模型利用CAD中的多线段命令构建了相应的几何图形，如图 3所示，并通过PFC2D的相关命令将几何模型导入PFC2D中。

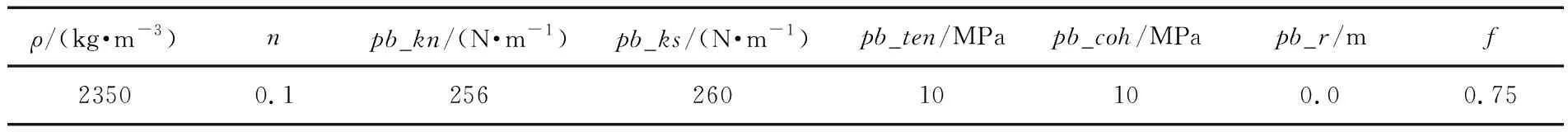
表 1 模型细观接触参数Tab.1 The meso-contact parameters of the model

以第一组数值模拟工况为例，颗粒粒径取1.0～1.4m，平均粒径1.2m，按照均匀分布的方式在图 3所示的红色矩形框中生成形状不规则的颗粒簇，并赋予线性接触模型参数，且设置法向和切向刚度以及摩擦系数，颗粒按照设定的孔隙率布满红色矩形区域，在此基础上通过时步迭代进行应力释放，并使之达到不平衡力极小的状态。对模型颗粒之间及颗粒与墙体之间赋予平行黏结模型参数，在重力作用下使模型重新达到平衡状态。最后进行削坡，并按照如图 3所示的①→②、③→④、⑤→⑥、⑦的顺序进行，每次削坡之后进行一次平衡。图 4给出了最终的分析模型示意图，模型顶宽20m，高30m，底宽140m，两侧坡面坡度比 1︰2。区域①中的颗粒在删除前充当预压的作用，使之达到相对密实的状态。每组试验模型中分别用不同粒径的颗粒模拟实际抛石防波堤的堆石料，颗粒形状仍然采用颗粒流双轴试验数值模拟中的不规则颗粒。在模型顶部中心位置处设置监测点A用来监测堤顶的竖向位移和速度。

1.4 参数选取

颗粒流数值模型中颗粒之间的接触参数进行标定，即通过数值模拟三轴试验和室内试验的结果对比分析，具体颗粒间接触参数详见表 1，表中pb_kn、pb_ks分别为颗粒法向刚度和切向刚度，pb_ten、pb_coh分别为法向黏结强度和切向黏结强度，pb_r为黏结半径，n为试样孔隙率，ρ为颗粒密度，f为摩擦系数。

2 数值结果分析

在图 1、2所示经调幅的输入地震动作用下，利用PFC2D分析得到了抛石防波堤地震反应，包括位移和加速度反应，并据此对抛石防波堤在输入地震动作用下的变形和加速度响应特征进行分析。

2.3.2 稳定性试验 取“2.2.2”项下供试品溶液（批号：20170508）适量，分别于室温下放置0、2、4、8、12、24 h时按“2.1”项下色谱条件进样测定，以橙皮苷峰的保留时间和峰面积为参照，记录各共有峰的相对保留时间和相对峰面积。结果，11个共有峰相对保留时间的RSD均小于0.50%，相对峰面积的RSD均小于0.79%（n＝6），表明供试品溶液于室温下放置24 h内基本稳定。

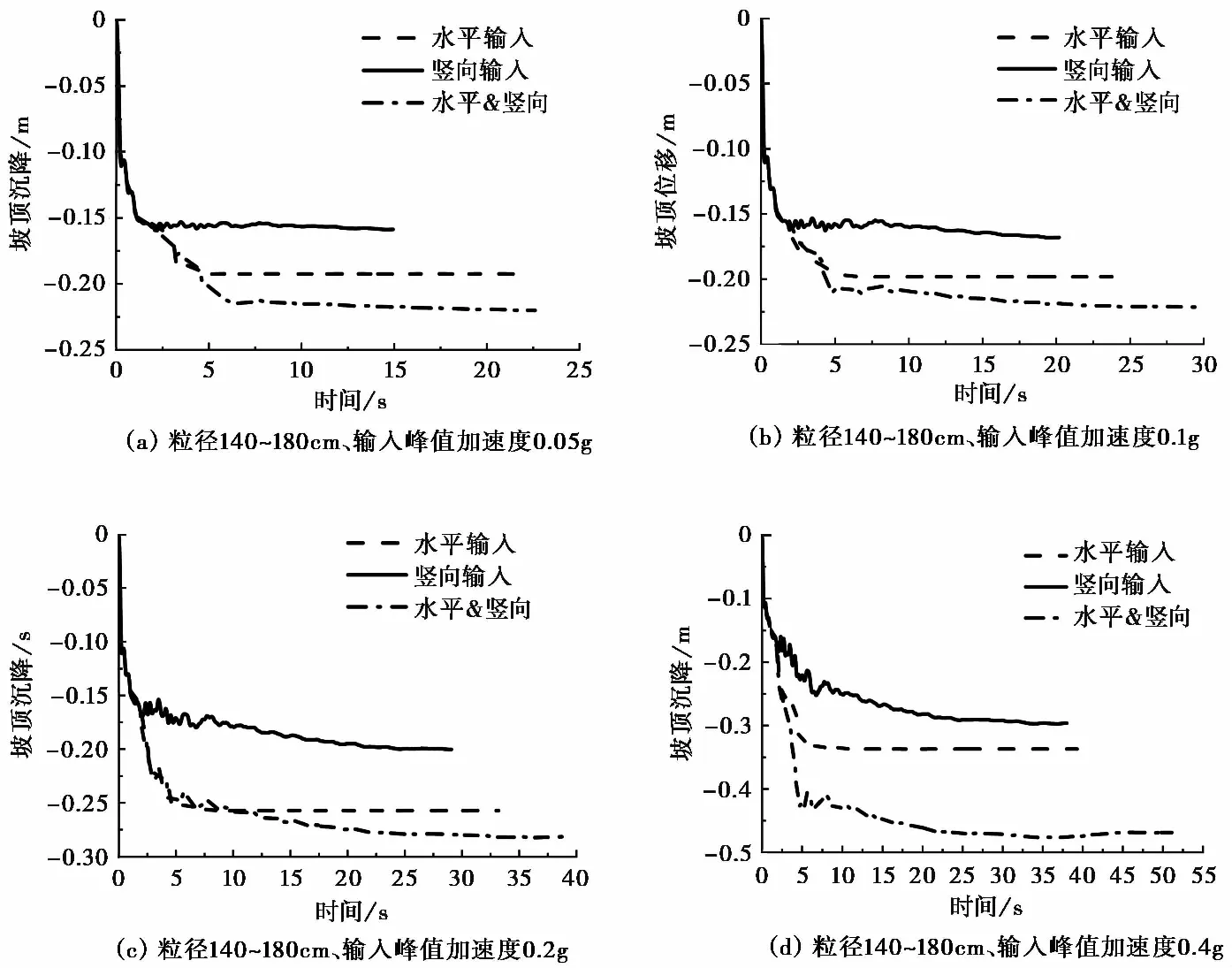
图 5 不同工况下坡顶沉降变化趋势Fig.5 Variation of slope top settlement under different working conditions

2.1 抛石防波堤坡顶沉降

(1)不同输入条件下坡顶沉降分析

图 5给出了坡顶中心A处的竖向位移随时间的变化规律。以图 5a为例，发现坡顶沉降受地震动输入方式影响较大，坡顶沉降量从大到小的顺序为：水平和竖向组合输入最大、单一水平输入次之、单一竖向输入最小。相关研究通常只对水平输入地震动下的抛石防波堤进行研究[3， 4，5， 9]，由图 5可以看出竖向输入对抛石防波堤变形的影响不可忽略。在颗粒流数值模拟中设定终止条件为模型达到稳定状态，由图 5可以看出，单一竖向加载时模型达到平衡状态所用时间最短，单一水平加载次之，水平和竖向组合加载最长。由此可知，在输入地震动作用下，抛石防波堤的稳定性受水平和竖向荷载组合作用时的影响最大，水平加载次之，竖向加载影响最小。

由图 5可以看出，3种加载方式最初的沉降速率比较一致，随后沉降速率逐渐减小。由输入的加速度时程曲线得知，随着时间的推移加速度幅值越来越小，大约20s后加速度很小。从定性角度分析，沉降速率逐渐减小的原因主要有：模型自身的内部结构随着地震动的输入在变化，加速度幅值在不断地减小。原始输入的加速度持时80s，但是所有模型记录的位移时程持时均未达80s，这表明加速度时程中加速度幅值极小时对抛石防波堤的稳定性几乎没有影响。

(2)峰值加速度对坡顶沉降的影响

依据不同工况下的抛石防波堤坡顶的最终沉降量，见表 2，分析了输入峰值加速度对坡顶沉降的影响，结果表明：所有工况在输入方式相同、颗粒粒径相同条件下，输入加速度峰值越大最终沉降量越大，所以抛石防波堤的稳定性受输入峰值加速度影响较大。

图 6给出了抛石防波堤在地震动输入方式相同时，坡顶最终沉降随输入加速度峰值的变化规律。由图 6可以看出输入条件相同时，峰值加速度越大，抛石防波堤最终的沉降量越大。如图6(a)和(c)所示，单一水平输入和水平与竖向组合输入时，输入峰值加速度相同，颗粒粒径越大最终沉降量越小。

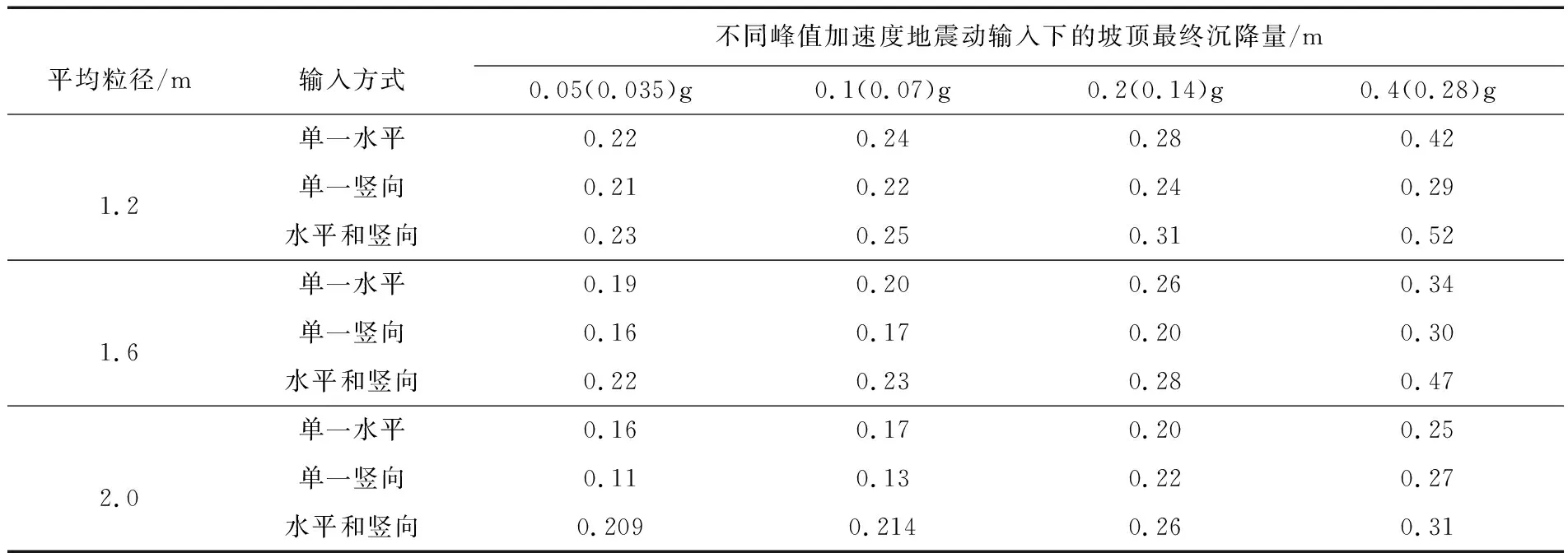
表 2 不同工况下坡顶最终沉降量统计结果Tab.2 The statistical results of final settlement of slope top under different working conditions

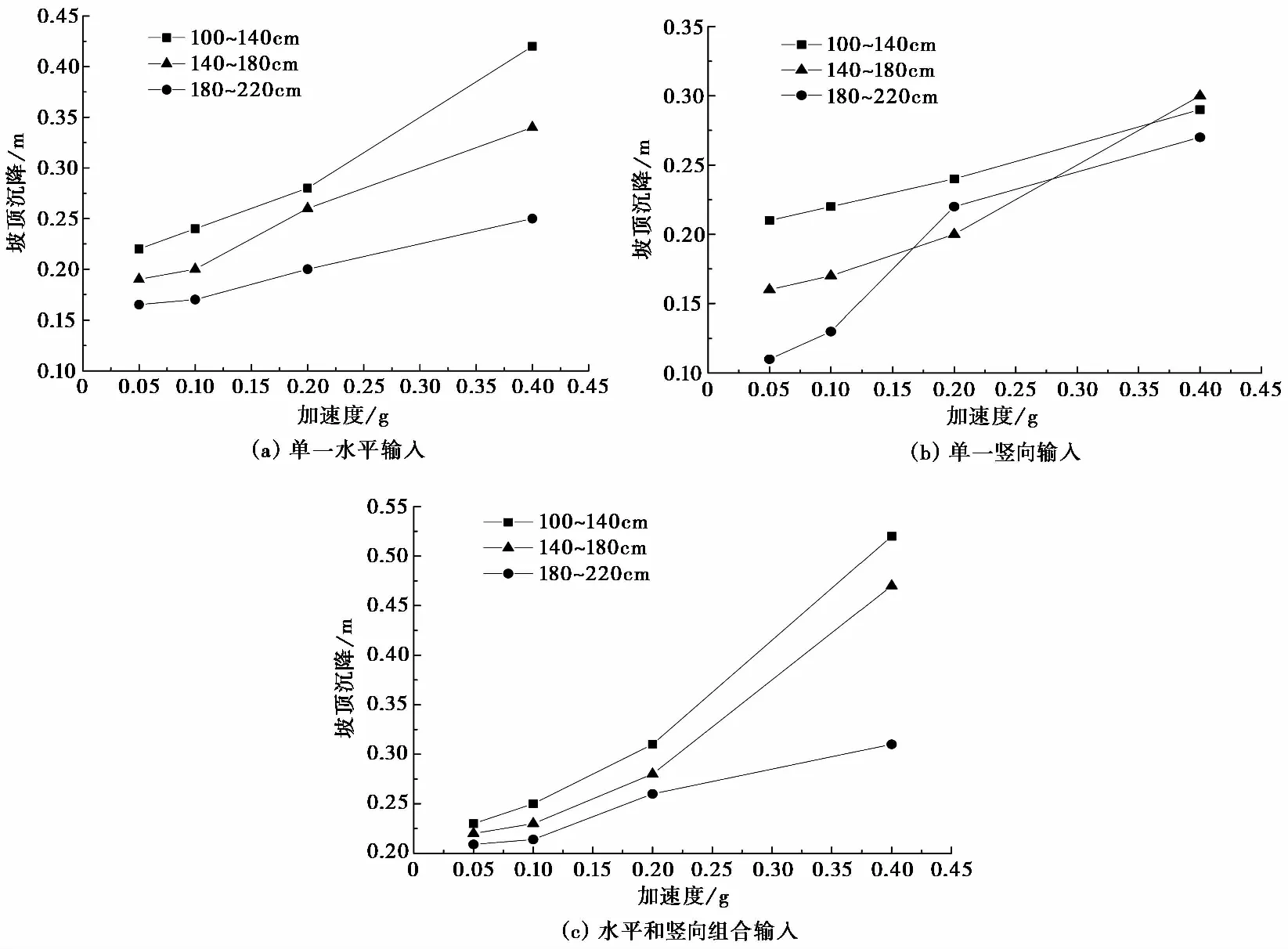
图 6 抛石防波堤坡顶沉降随地震动峰值加速度的变化趋势Fig.6 Variation of slope top settlement of rubble-mound breakwater with peak acceleration of ground motion

较大粒径颗粒组成的堆石料颗粒之间的咬合作用大于小粒径颗粒组成的堆石料，表现为大粒径堆石料整体抗剪强度大于小粒径堆石料，由此可以看出相同输入地震动下，颗粒流数值模拟得到的剪应力引起的大粒径颗粒模型变形小于小粒径颗粒模型的变化规律是合理的。然而，竖向输入加速度峰值小于0.1g时，颗粒粒径越小坡顶的最终沉降量越大； 当竖向峰值加速度0.2g时，平均粒径为120cm的最终沉降量最大，平均粒径200cm的次之，平均粒径 160cm的最小； 竖向峰值加速度0.4g时，平均粒径的最终沉降量排序为200cm>120cm>160cm。由此可知，单一竖向加载最终沉降量变化规律不同于单一水平加载、水平与竖向组合加载，说明了最终沉降量不仅与输入峰值加速度有关，还与加载方式有关。单一竖向输入时颗粒应力以正应力为主，单一水平输入时颗粒应力以剪应力为主，水平和竖向同时输入时内部应力比较复杂，所以竖向作用引起的抛石防波堤沉降规律与其它两种作用方式不同。

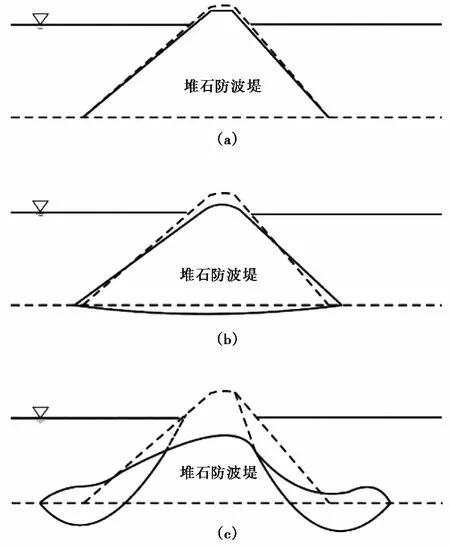
图 7 抛石防波堤典型的破坏模式[6]Fig.7 Typical failure modes for rubble-mound breakwaters[6]

图 8 工况12抛石防波堤初始模型与输入地震动作用下变形模型Fig.8 Theinitial model of rubble-mound breakwater and the deformation model under input ground motion under working condition 12

2.2 抛石防波堤破坏模式

抛石防波堤在地震动作用下有3种典型的破坏模式[5]，如图 7所示。图 7(a)为抛石防波堤在地震作用下上部结构发生不均匀沉降； 图7(b)为地震作用下，抛石防波堤地基沉降或地基液化引起的坡顶沉降及横向变形或上部结构不均匀沉降； 图7(c)为地震引起地基液化，从而导致结构失稳或上部沉降及倾覆。颗粒流数值模拟结果表明，相对几何尺寸较大的模型，在地震动作用下模型的变形较小，所以在分析抛石防波堤破坏模式时选取所有工况中变形最大的一组，即平均颗粒粒径为120cm，地震动为水平和竖向组合输入下，峰值加速度分别为0.4g和0.28g的工况。该工况下抛石防波堤初始模型与输入地震动作用下变形模型如图 8所示，由图可以看出初始模型边界颗粒紧贴模型几何构造线边缘，在加载达到稳定状态以后，上部两侧坡体及坡顶均与原始模型构造线有所偏离。从模型的破坏变形模式可以看出与图 7(a)所示的变形规律一致，由此验证了利用颗粒流离散元进行抛石防波堤动力响应数值分析的可行性。

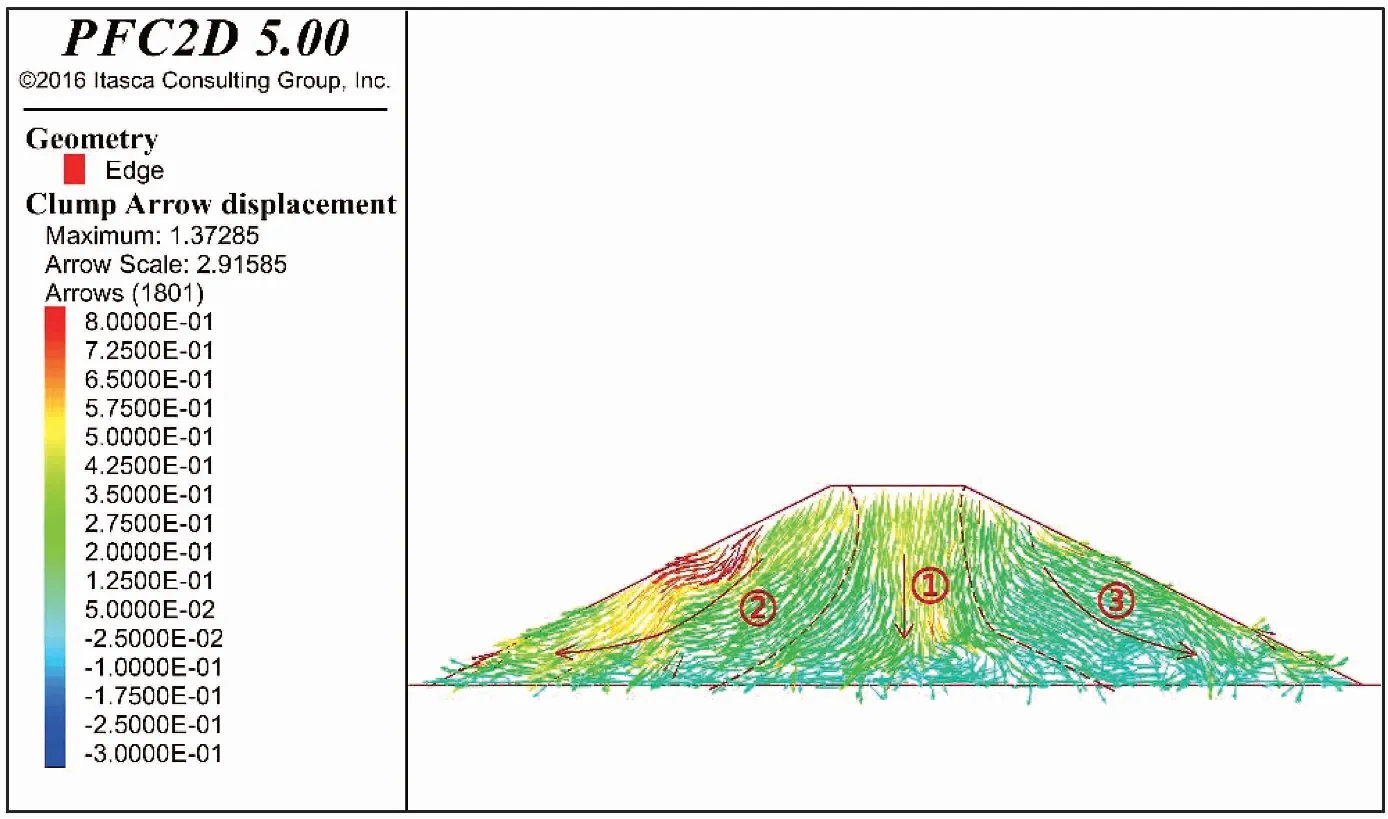
图 9 工况12抛石防波堤位移矢量图(单位：m)Fig.9 Displacement vector diagram of rubble-mound breakwater under working conditions 12(unit： m)

表 3 坡顶峰值加速度放大系数统计结果Tab.3 Statistical result of peak acceleration amplification factor at slope top

图 10 监测点A峰值加速度放大系数随输入地震动峰值加速度变化趋势Fig.10 Variation of acceleration amplification coefficient with peak acceleration of input strong motion at monitoring point A

为便于更清晰地了解抛石防波堤在地震动作用下的变形机制，将以上工况对应的位移矢量图进行深入分析。由图 9可以看出，区域①主要以竖向沉降为主，两侧坡体②和③分别斜向下滑动，坡面表层滑动，其主要原因是坡体内部受侧向约束力较大，因此区域①变形以竖向变形为主，而两侧坡体面向凌空面，坡面无侧向约束，故而受力主要为竖向正应力和水平向的侧压力，由此引起的区域②和③既有竖向位移也有水平位移，即总位移方向斜向下。此外，尽管坡体几何对称，但内部堆石颗粒结构不对称，其材料存在各向异性，从而导致左右坡体变形不完全对称，且左侧坡面的浅层滑动略大于右侧坡面。同时，抛石防波堤颗粒流数值模拟显示两侧坡脚处颗粒有明显向外运动的趋势，因此在抛石防波堤工程设计中宜考虑坡脚的这种变形，采取相关措施加以控制。

2.3 加速度响应特征

依据计算峰值加速度可统计得到水平输入地震动下各工况坡顶峰值加速度放大系数，统计结果列于表 3，峰值加速度放大系数随输入地震动峰值加速度的变化关系如图 10所示。由图 10和表 3可以看出，同一个模型，颗粒粒径相同时，峰值加速度放大系数随输入地震动峰值加速度增大而逐渐减小，且峰值加速度小于等于0.10g时放大系数衰减较快，随着输入峰值加速度增加放大系数衰减逐渐变小； 相同输入峰值加速度下，颗粒粒径越大加速度放大系数越大。由此可得出，输入峰值加速度越大，抛石防波堤发生的变形越大，耗散的地震动能量越多； 相同输入峰值加速度下，大粒径模型发生的变形较小，小粒径模型发生的变形大，同样由于小粒径的颗粒消耗的能量更多，所以粒径越小峰值加速度放大系数越小。

3 结论

基于颗粒流离散元方法分析了抛石防波堤在输入地震动作用下的动力响应，在此基础上研究了不同粒径颗粒构成的抛石防波堤在地震动作用下的变形特征。输入地震动引用鲁甸地震中龙头山强震动台站记录到的南北向和竖向的加速度时程，离散元数值模拟中输入方式分别为单一水平向输入、单一竖向输入及水平和竖向组合输入。经过对离散元数值模拟结果进行分析，得出的主要结论如下：

(1)当颗粒粒径相同时，输入峰值加速度相同，发现抛石防波堤在水平和竖向组合输入时坡顶沉降最大，单一水平向输入次之，单一竖向输入最小； 当颗粒粒径相同、输入方式也相同时，抛石防波堤坡顶沉降随输入峰值加速度的增大而增大； 单一竖向输入防波堤坡体达到稳定状态用时最短，水平和竖向组合输入时用时最长，单一水平向输入时用时介于二者之间。

(2)当颗粒粒径相同时，抛石防波堤坡顶峰值加速度放大系数随输入峰值加速度的增加逐渐减小，且输入峰值加速度越大衰减越慢； 相同输入峰值加速度时，抛石防波堤坡顶的峰值加速度放大系数受粒径影响较大，颗粒粒径越大峰值加速放大系数越大，反之，颗粒粒径越小峰值加速度放大系数越小。

(3)本研究所得到的抛石防波堤变形特征与其在地震动作用下的经典变形特征相符，表明通过离散元数值模拟抛石防波堤在地震动作用下的动力响应是可行的。抛石防波堤在地震动作用下的变形特征表明，刚性地基上的抛石防波堤受地震动作用主要表现为坡顶沉降，两侧坡体斜向下滑动，且表面存在浅层滑动变形，由于内部结构具有不对称性和各向异性，所以抛石防波堤变形不完全对称。两侧坡脚有向外运动的趋势或已发生向外变形，所以有必要在抛石防波堤工程设计和施工中采取相关措施，以防止坡脚在地震动作用下发生破坏。