科技文档间非对称关系的双模态度量方法

徐建民,王鑫

(河北大学 网络空间安全与计算机学院，河北 保定 071002)

文档间关系度量研究是近年来多个领域的一个研究热点，在文档分类、抄袭检测、自动问答、智能检索等领域都有着广泛的应用[1].传统度量方法多假设文档间关系是对称的，不区分文档间关系的方向差异性，未能刻画出2个文档之间相互影响力的不同.Garg等[2]指出文本文档间存在非对称关系并提出了一种度量方法，实验证明了非对称关系度量与传统的对称度量方法相比具有更好的性能.

科技文档不同于文本文档，它是一种多模态数据，除文本外，还包括公式、图表等重要信息[3]，很多时候科技文档中的这些非文本信息更能代表相关文档的内涵.这些非文本信息之间的关系本质上来看也不是对称的，忽略这种非对称关系，或将已有的文本文档间非对称关系度量方法直接用于度量科技文档间非对称关系会造成度量数据的不准确乃至产生较大偏差.

本文在对科技文档间非对称关系进行分析的基础上，提出一种基于文本和公式双模态的度量方法.该方法将非对称关系定义为覆盖度，通过融合公式覆盖度和文本覆盖度得到文档覆盖度，以实现对科技文档间非对称关系的度量.新方法可以更好地区分科技文档间关系的方向性，更准确地度量科技文档间关系.本文的主要贡献包括：

1)针对科技文档间的非对称关系，提出文档覆盖度的概念，给出了文档覆盖度的规范定义.

2)提出一种基于非对称因子的公式覆盖度计算方法，并基于TCM(Tversky contrast model)[4]思想对公式进行了改进，在此基础上线性组合公式覆盖度和文本覆盖度得到科技文档的覆盖度.

1 相关研究

目前，已有的科技文档间关系的度量方法多是基于对称关系的，主要分为4类：1)基于向量空间模型的方法.刘勘等[5]提出一种基于改进TF-IDF特征词加权算法的科技文档聚类方法，根据特征词的词频、所在位置和词性为特征词加权，建立科技文档向量空间模型，利用该模型计算文档相似度.牛奉高等[6]通过共现分析挖掘科技文档特征词间的语义关系，实现对向量空间模型的改进，利用改进模型计算文档间相似性.2)基于集合模型的方法.Jiang等[7]提出一种基于N-Gram的安全相似文档检测(SSDD)协议，考虑N-Gram模型具有识别重叠文本片段的优点，利用该模型计算文档相似性.徐建民等[3]提出一种结合公式和文本的科技文档相似度计算方法，公式相似度基于集合模型的思想得到，将公式相似度和文本相似度线性融合计算科技文档相似度.3)基于层次结构的方法.楼雯等[8]将文档转换为本体树结构，利用本体中概念的相似程度计算文档间相似性.黎雪微等[9]利用本体和信息量融合的相似度算法来改进基于内容的推荐方法中的文本项目过于集中的问题，提出在推荐时同时考虑项目信息距离和信息损失距离的相似度.4)基于引文图的方法.朱戈等[10]提出一种基于改进PageRank的科技文档相似性搜索算法，结合文档内容和文档间引用关系对PageRank算法进行改进，基于改进算法计算文档相似度.翟玲等[11]提出一种基于分段估计和PageRank的文档相似性搜索算法，该算法采用分段估计法对文档特征进行提取；并将PageRank取值大小作为文档初步分类的准则，计算文档不同特征的相似度.上述方法均基于文档间对称关系的假设，未考虑科技文档间关系的非对称性.

Chen等[12]发现在一个文档集合中任意2个术语间的关联是非对称的，提出了用术语共现算法来衡量术语间非对称关系.在术语间非对称关系发现后，相关专家学者从文本结构、文本内容等角度开展了文档间非对称关系的研究.从文本结构角度：Guan等[13]提出一种称为种子亲和传播的文档聚类算法，通过获取文本的结构信息来度量文档间的非对称关系，并定义了相同特征集合、独特特征集合、显著相同特征集合来表示文本的结构信息.Chua等[14]用TCM思想来度量本体间非对称相似性，并将这种非对称相似性用于解决本体对齐的问题.Albertoni等[15]提出一种本体实例间的非对称语义相似度计算方法，考虑了实例间结构的比较，用非对称性来强调实例特征间的包含原则.部分学者还从文本内容角度进行了研究：Yoshida等[16]提出用修正重叠系数来衡量文档间非对称关系，并将文档关系的非对称性应用到信息过滤系统中，从相似的文档中选择代表性文档.Teitelbaum等[17]提出一种基于非对称距离的相似函数，利用偏斜范数来度量文本间非对称关系.宋韶旭等[18]提出一种文本非对称相似度计算方法，并在此基础上利用非对称相似度矩阵对文本进行了聚类分析.Wu等[19]提出了一种新的非对称文本相似性公式，该公式汇总了由不同双线性参数矩阵参数化的逐层文本相似性，最后通过实验在3个公共数据集上证明了公式的有效性.上述工作的研究对象为文本文档间非对称关系，没有考虑科技文档多模态数据的特殊性，不能直接用于科技文档间非对称关系的计算.

2 科技文档的表示及非对称关系分析

2.1 科技文档的多模态表示

科技文档具有多模态的特征，除文本信息外，一般还包括公式和图表.相对于文本的多义性和图表的易改动性，公式具有国际通用、不易修改等特征，可以更准确地描述科技文档的内容及其文档内容内在的逻辑关系,不失一般性.本文以数学公式为例论述.

借鉴文献[3]的做法，本文将一篇科技文档表示为一个二元组：di=(Fi,Ti)，其中Fi表示公式部分，Ti表示文本部分.

2.1.1 公式部分的表示

一篇科技文档中的公式可分为独立公式和内嵌公式.独立公式通常单独作为一行出现且不包括文本；内嵌公式一般出现在独立公式附近的上下文中，与文本交杂在一起[20].由于大部分内嵌公式是对独立公式的说明，因此本文只考虑独立公式.

一个独立公式可以由一个有序特征元素构成的字符串表示.特征元素包括运算符、常量和括号等[21].

科技文档di中的第k个公式可以表示为

(1)

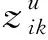
于是，科技文档中公式部分可以表示为一个集合Fi，即

Fi={fi1,fi2,…,fik,…,fie},

(2)

其中，fik表示文档di中第k个公式;e表示文档di中包含的公式数量.

2.1.2 文本部分的表示

文本部分Ti用向量空间模型表示.该方法将Ti表示为特征向量，Ti的每个特征词看作是特征向量的独立一维，并将特征词的权重作为每一维的坐标值，即

Ti=(ti1,wi1),(ti2,wi2),…，(tik,wik),…，(tim,wim)，

(3)

其中，tik表示Ti中的第k个特征词；wik表示特征词tik在Ti中的权重；m表示Ti中包含特征词的数量.对于Ti中每个特征词,其权重用TF-IDF[22]方法计算得到.

2.2 科技文档间非对称关系分析

文献[23]提出对象间关系存在非对称的情况，并提供了对象间非对称关系的经验证据.例如“a就像b”，它有一个主语“a”，一个指示对象“b”，它一般不等同于相反的相似性描述“b就像a”，这是因为人类的记忆联想过程是非对称的[12].在实际应用中科技文档间也存在非对称关系，即对于任意2篇科技文档A、B，sim(A,B)≠sim(B,a).这种非对称关系反映了科技文档间关系的方向性或者包含关系.

科技文档中的公式表示为一个集合.按照集合论的原理，2篇科技文档公式集合间的关系可以分为其交集为空、交集非空2个集合互不为子集、交集非空一个集合是另一个集合的子集3种情况.交集为空表示2篇文档的公式之间没有关系，非空互不为子集表示2篇文档内容有相同性，一个集合是另一个集合的子集表示它们的内容具有包含性.表1给出了2篇科技文档di、dj中公式部分关系的一个示例.

表1 公式部分示例

科技文档中的文本部分表示为词语的特征向量，每一个特征词都具有一定的权重.这时，2篇文档的特征词集合可能相同，也可能不同.相同特征词的权重可能相等，也可能不相等.表2给出了2篇科技文档di、dj中文本部分关系的一个示例.

表2 文本部分示例

由表1、表2可以看出对文档di和dj，文档di公式和特征词包含在文档dj中，而文档dj中除了和文档di相同的公式、特征词外，还有其他的公式、特征词，而且相同特征词的权重也不相同.从不同文档角度来看，di对dj的覆盖程度与dj对di的覆盖程度是不同的，并且di对dj的影响明显小于dj对dj的影响.

3 科技文档覆盖度及其度量

本文用文档覆盖度来度量科技文档间的非对称关系，包括公式覆盖度和文本覆盖度2部分.

公式覆盖度利用改进的非对称因子方法计算，反映了2个文档包含的公式集合之间的非对称关系；文本覆盖度利用文本间相对突出性计算，反映了科技文档间文本的非对称关系.

3.1 科技文档间公式覆盖度计算

定义1科技文档的公式覆盖度：对任意2篇文档di、dj，di对dj公式覆盖度定义为di中公式对dj中公式的包含程度，记为CF(Fi,Fj)，0≤CF(Fi,Fj)≤1.

科技文档公式覆盖度可以通过2个文档所包含公式集合之间的覆盖度来计算，具体分为2步：第1步计算任意2个公式间的相似度，第2步计算2篇科技文档的公式覆盖度.

3.1.1 2个公式的相似度计算

公式fiq和fjs间的相似度sim(fiq,fjs)可以通过比较公式特征元素字符串的方式得到，计算公式如式(4)所示.

(4)

公式的特征元素字符串指能唯一标识公式本身的字符串，其获得方法可参考文献[3]和[24]，基本过程如下：先对公式预处理，把公式符号进行统一化处理；然后解析公式的结构，生成与之对应的二叉树，并对二叉树进行归一化；最后中序遍历规范化后的二叉树，得到公式特征元素字符串.

3.1.2 科技文档公式覆盖度计算

3.1.2.1 公式集合间的非对称因子

定义2公式集合间非对称因子：对于任意2个文档的公式集合Fi={fi1,fi2,…,fir}，Fj={fj1,fj2,…,fjp}，Fi和fj的非对称因子是指2个公式集合的相同公式在公式集合Fi中所占的比例，计算公式如式(5)所示.

(5)

同理，Fj和Fi的非对称因子指2个公式集合的相同公式在公式集合中所占的比例，计算公式如式(6)所示.

(6)

其中，|Fi∩Fj|、|Fj∩Fi|表示公式集合Fi和Fj中相同公式的数目，|Fi|表示公式集合Fi中公式的数目，|Fj|表示公式集合Fj中公式的数目.

3.1.2.2 公式集合的覆盖度

公式(5)中，当Fi≠ø且|Fi∩Fj|=|Fi|时，没有考虑|Fi|的大小不同.例如|Fj|=30时，|Fi∩Fj|=|Fi|=10和|Fi∩Fj|=|Fi|=20两种情况，得到的CF(Fi,Fj)值都为1.但第1种情况中Fj的30个公式，包含了Fi的10个公式，而第2种情况是Fj的30个公式，包含了Fi的20个公式.Fi的大小不同，则Fj对Fi覆盖的程度也不同.同理，公式(6)也存在同样的问题.

针对公式(5)和(6)的不足，可依据TCM的思想对其进行改进.TCM思想由Tversky提出，用来度量特征权值为布尔类型的对象间相似关系.该思想假设每个对象都由一组特征来描述，对象间的相似性由对象间的相同特征和独特特征共同决定.改进后的计算公式如式(7)、(8)所示.

(7)

(8)

其中，|Fj-Fi|表示在公式集合Fj中出现但不在公式集合Fi中出现的公式数目，反映了Fj的独特特征，|Fi-Fj|表示在公式集合Fi中出现但不在公式集合Fj中出现的公式数目，反映了Fi的独特特征.α为调和因子，反映了对象的独特特征对非对称关系的影响，0<α≤1.当α=1时，CF(Fi,Fj)=CF(Fj,Fi).

3.2 科技文档的文本覆盖度计算

定义3科技文档的文本覆盖度：对于任意2篇科技文档di、dj，di对dj的文本覆盖度指di中文本与dj中文本的包含程度，记为CV(di,dj).

文献[25]认为对象间相似性由特征相似性和特征的突出性共同决定，据此，本文给出了特征词的突出性和文本间相对突出性的定义及计算方法，并将文本相对突出性用于修订传统的对称相似度，给出文本覆盖度的计算方法.

定义4特征词的突出性：对于任意2个文本Ti和Tj中的相同特征词tik、tjk(tik=tjk)，特征词tik的突出性是指tik的权重与tik、tjk权重之和的比值，计算公式如下：

(9)

定义5文本间相对突出性：对于任意2个文本Ti和Tj，文本Ti相对于Tj的相对突出性是指文本Ti和Tj中所有特征词突出线性和之比，计算公式如(10)所示.

(10)

同理，可以利用式(11)计算文本Tj相对于Ti的相对突出性.

(11)

计算得到文本间相对突出性后，用相对突出性调整余弦相似度，可以得到从Ti角度和Tj角度的文本覆盖度计算公式，如式(12)、(13)所示.

(12)

(13)

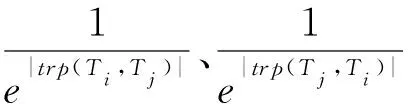
3.3 科技文档覆盖度计算

有了公式覆盖度和文本覆盖度的概念，可以得到科技文档覆盖度的定义.

定义6科技文档的覆盖度：任意2篇文档di和dj，di对dj的覆盖度定义为文档di和dj的文本覆盖度和公式覆盖度的线性组合，记为ARM(di,dj).

科技文档di对dj的覆盖度体现了文档di对dj的包含程度.从di角度给出科技文档覆盖度计算公式如式(14)所示.

ARM(di,dj)=βCF(Fi,Fj)+(1-β)CV(Ti,Tj).

(14)

同理可得科技文档dj对di的覆盖度计算公式，如式(15).

ARM(dj,di)=βCF(Fj,Fi)+(1-β)CV(Tj,Ti).

(15)

式(14)、(15)中的β为可调节的参数，用来调节公式和文本覆盖度对科技文档覆盖度的贡献程度，0≤β≤1.当β=1时，式(14)、(15)用来度量科技文档间公式的覆盖度；当β=0时，式(14)、(15)用来度量科技文档间文本的覆盖度.

4 实验

为验证本文提出的科技文档间非对称关系度量方法的有效性，实验部分与文献[3]、[26]提出的2种科技文档间关系度量方法作对比实验.表3为实验所涉及的方法及其解释.借鉴文献[27]的实验思路，先用3种方法分别计算数据集中任意2篇科技文档间的关系度量值，将得到的关系度量值作为k-means算法的输入，分别进行聚类实验，分析比较3种方法进行聚类实验的聚类效果.

表3 方法简写及其解释

4.1 数据集的构建及数据预处理

目前，信息检索领域尚无通用的中文科技文档数据集，因此本文参照信息检索领域中小型数据集的构建方法[28]，构建了一个满足实验需求的小型科技文档数据集，该数据集包括 500篇中文科技文档，涉及贝叶斯网络、个性化推荐、图像识别、文本分类和舆情监测5个主题.依据文献[3]对数据集的处理方法，本文选取该数据集的60%作为训练集，40%作为测试集，对数据集中每个主题的文档亦按此比例采用随机抽取的方法分割训练集和测试集.由于实验数据集较小，为了从有限数据集中获取更多的有效信息，提高实验的可信性，本文实验过程中采用了交叉验证的方法.

数据集构建完成后，为得到文档中公式和文本信息，须进一步对文档进行如下处理：1)提取每篇文档中的公式和文本.公式保存为pdf格式，文本保存为txt格式.2)公式预处理.借助Mathpix Snipping Tool工具对所有公式进行解析，得到每篇文档LaTeX格式的公式字符串，整理并存入txt文件中.3)文本预处理.先对所有文本进行中文分词，利用哈工大停用词表做停用词处理；再统计每个文本的词频，根据实验需要，选取前50个高频词作为文本特征词；最后计算所有特征词的tf-idf值.

4.2 聚类性能评价指标

4.2.1 单个聚类结果簇评价标准

1)熵

熵表示一个系统内的混乱程度，也常用来衡量聚类的效果.熵值越低，聚类结果簇内部混乱程度越小，聚类效果越好.熵值计算公式如式(16)[6]所示.

(16)

2)准确率

准确率用来衡量聚类的准确性，聚类结果簇准确率计算公式如式(17)[18]所示.

(17)

4.2.2 多个聚类结果簇评价标准

对于多个聚类结果簇，用平均熵值和平均准确率来衡量聚类效果，如式(18)、(19)所示.

(18)

(19)

其中，eave-n表示平均熵值；Eave-n表示平均准确率，n表示结果簇数目.

4.3 实验结果及分析

本文采用蒙特卡洛交叉验证，将数据集按6∶4比例随机划分为训练集和测试集，这样进行多次单独的训练和验证，使聚类效果达到最优，最后将测试集上的验证结果取平均值作为最后的结果.实验分为3步：第1步是科技文档中公式聚类性能的比较；第2步是科技文档中文本聚类性能的比较；第3步是融合公式和文本2部分的科技文档聚类性能的比较.在每一步中，对覆盖度值进行聚类时距离的选择均参考文献[29].

4.3.1 公式聚类性能的比较

设定实验聚类结果簇数从5递增到85，步长为20，为得到公式覆盖度计算的参数，以平均熵值和平均准确率为评价指标，在公式训练集上反复训练，获得最优值，并在公式测试集上加以验证.分别计算参数α=0.1，0.2,…,0.9时，公式覆盖度值对公式测试集聚类性能的影响，结果如表4所示.

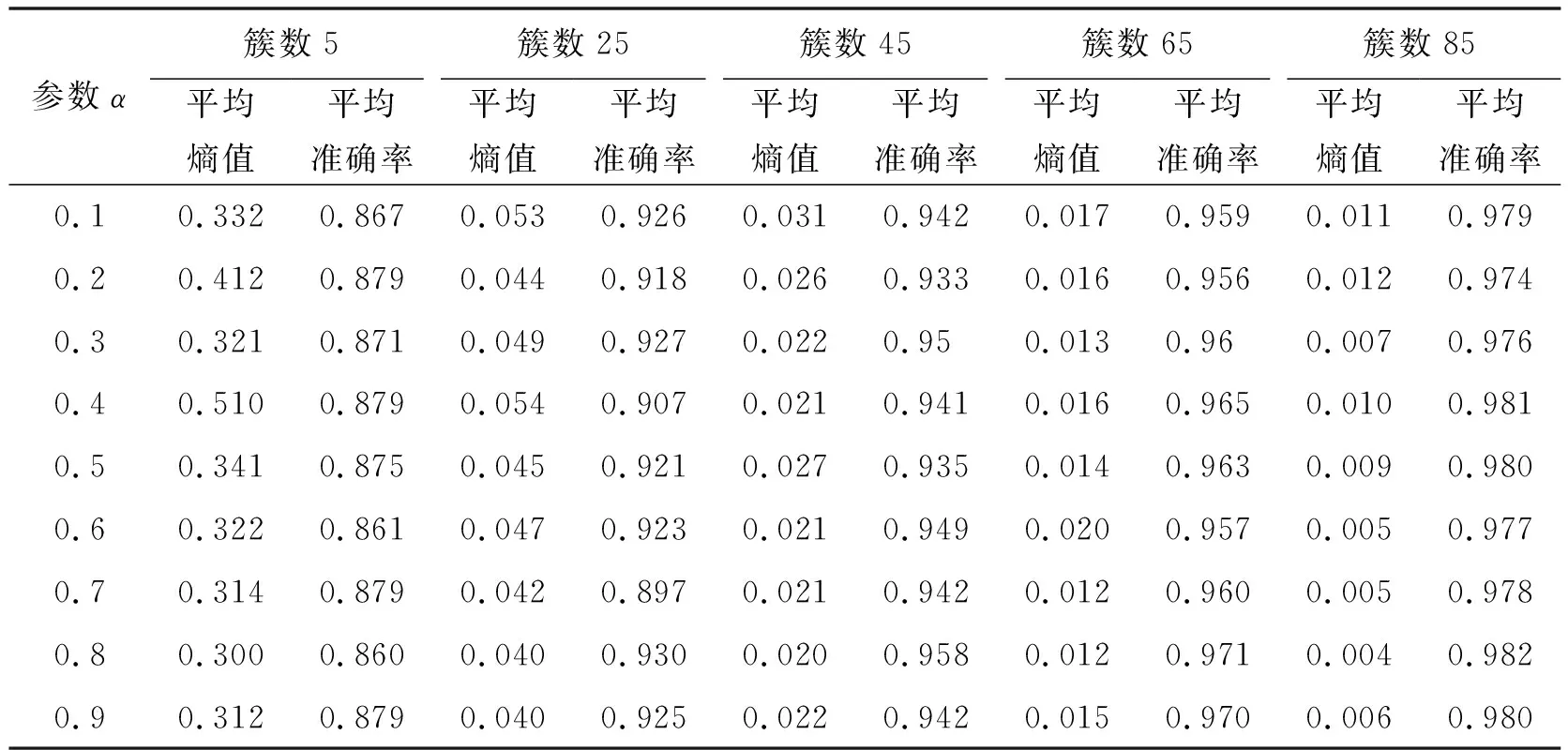
表4 不同α值公式聚类的平均熵值和平均准确率

通过对表4中数据进行观察和分析，从整体上看，α取0.8时，结果簇的聚类性能最好.后续实验将α=0.8作为公式覆盖度计算的参数值.但是从表4也能看出当α=0.1,0.2,…,0.9时，不同结果簇的平均熵值和平均准确率相差不大，这是因为本文在提取文档公式信息时方法比较粗糙，求得的公式覆盖度存在数据稀疏问题.为取得更好的效果，对公式的处理今后研究中可尝试改进.

SMM、SMM1、ASYM方法的公式部分关系度量在不同结果簇数下的平均熵值和平均准确率对比图，如图1所示.

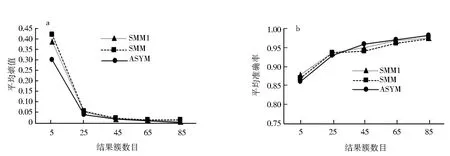
a.平均熵值对比;b.平均准确率对比.图1 SMM、SMM1、ASYM方法公式关系度量性能对比Fig.1 Performance comparison of SMM，SMM1 and ASYM method of formulas

图1a为SMM、SMM1、ASYM方法公式部分关系度量平均熵值的比较，从图1a中可以看出，当结果簇数目从5到85时，ASYM方法的平均熵值均小于SMM、SMM1方法的平均熵值.图1b为SMM、SMM1、ASYM方法公式部分关系度量平均准确率的比较，从45簇到85簇，ASYM方法的平均准确率均大于SMM、SMM1方法的平均准确率.当结果簇数目从5到25时，ASYM方法的平均准确率小于SMM、SMM1方法的平均准确率.实验结果表明并不是所有科技文档间公式的非对称度量聚类效果都比对称度量聚类效果好，但大部分情况下公式的非对称度量聚类效果优于对称度量.一些科技文档间公式的非对称关系明显，对于这些科技文档，用本文方法进行聚类效果更好，这是因为非对称度量能更好地区分文档间公式，衡量文档间公式的关系.

4.3.2 文本聚类性能的比较

SMM、SMM1、ASYM方法文本部分关系度量在不同结果簇数下的平均熵值和平均准确率对比，如图2所示.

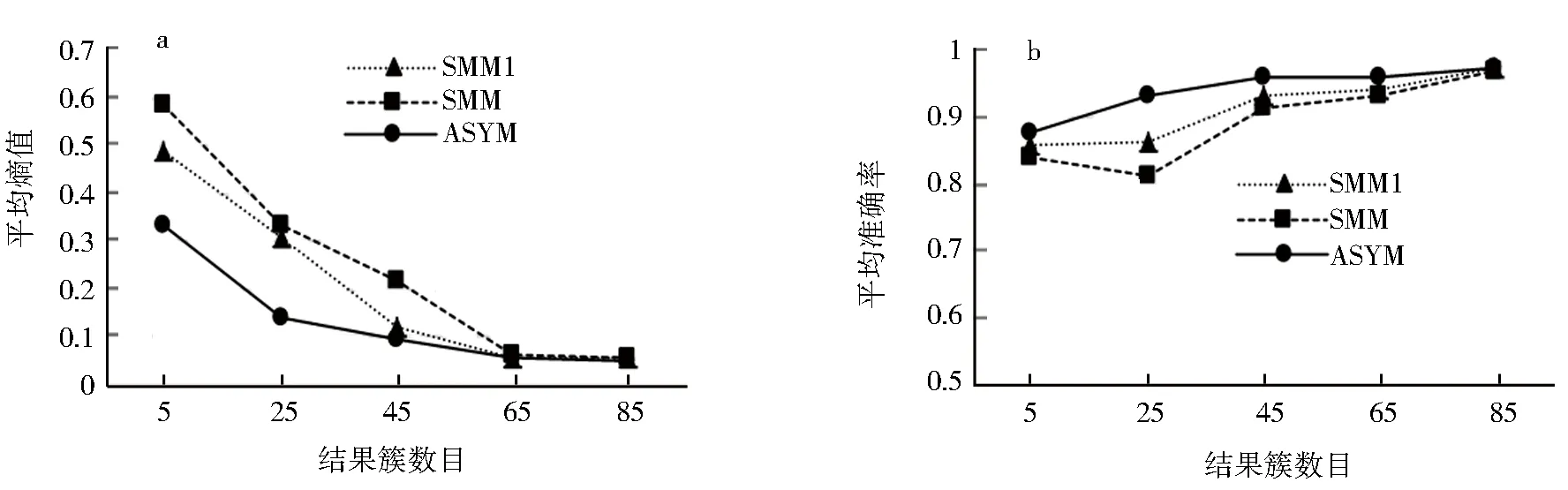
a.平均熵值对比;b.平均准确率对比.图2 SMM、SMM1、ASYM方法文本关系度量性能对比Fig.2 Performance comparison of SMM，SMM1 and ASYM method of texts

图2a为SMM、SMM1、ASYM方法文本部分关系度量平均熵值的比较，从图2a中可以看出，结果簇数目从5到65，ASYM方法的平均熵值小于SMM、SMM1方法的平均熵值.当结果簇数目从65到85时，3种方法的平均熵值曲线大致重合.图2b为SMM、SMM1、ASYM方法文本部分关系度量平均准确率的比较，结果簇数目从5到85，ASYM方法平均准确率大于SMM、SMM1方法的平均准确率.图2a、b可看出在本文数据集的不同结果簇数下，文本使用非对称度量进行聚类的效果均优于对称度量，并且聚类性能提升明显.产生这种结果的原因是非对称度量考虑了文本间非对称关系，能更好地区分文本差异性，提高文本关系度量的准确性.

4.3.3 融合公式和文本的科技文档聚类性能的比较

科技文档覆盖度计算公式中的β值，不同的文档类别中应有不同的取值.当β=0，0.1，0.2，…，1时，运用SMM、SMM1和ASYM方法分别计算对测试集聚类性能的影响，结果如表5～8所示.

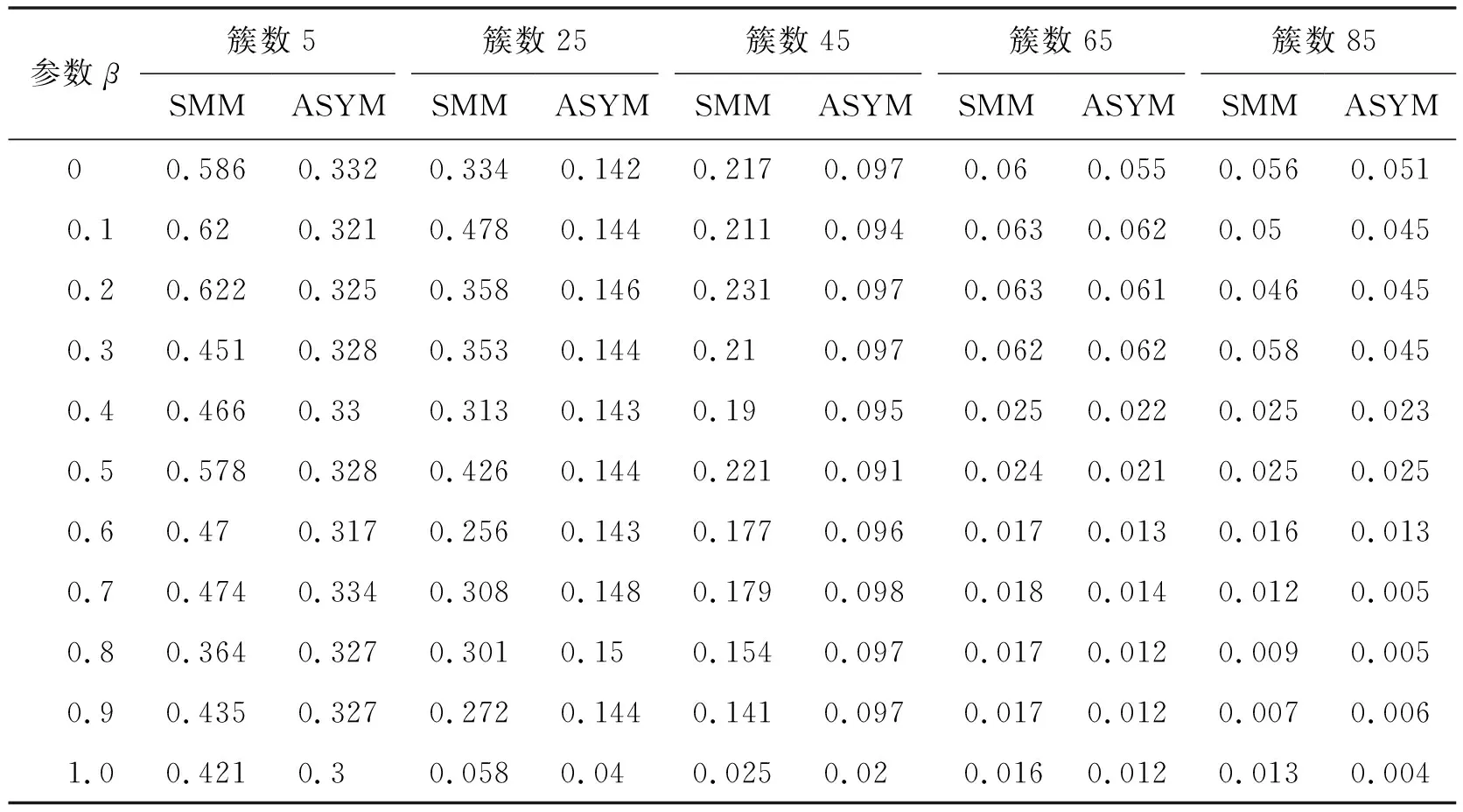
表5 不同β值SMM方法和ASYM方法的平均熵值

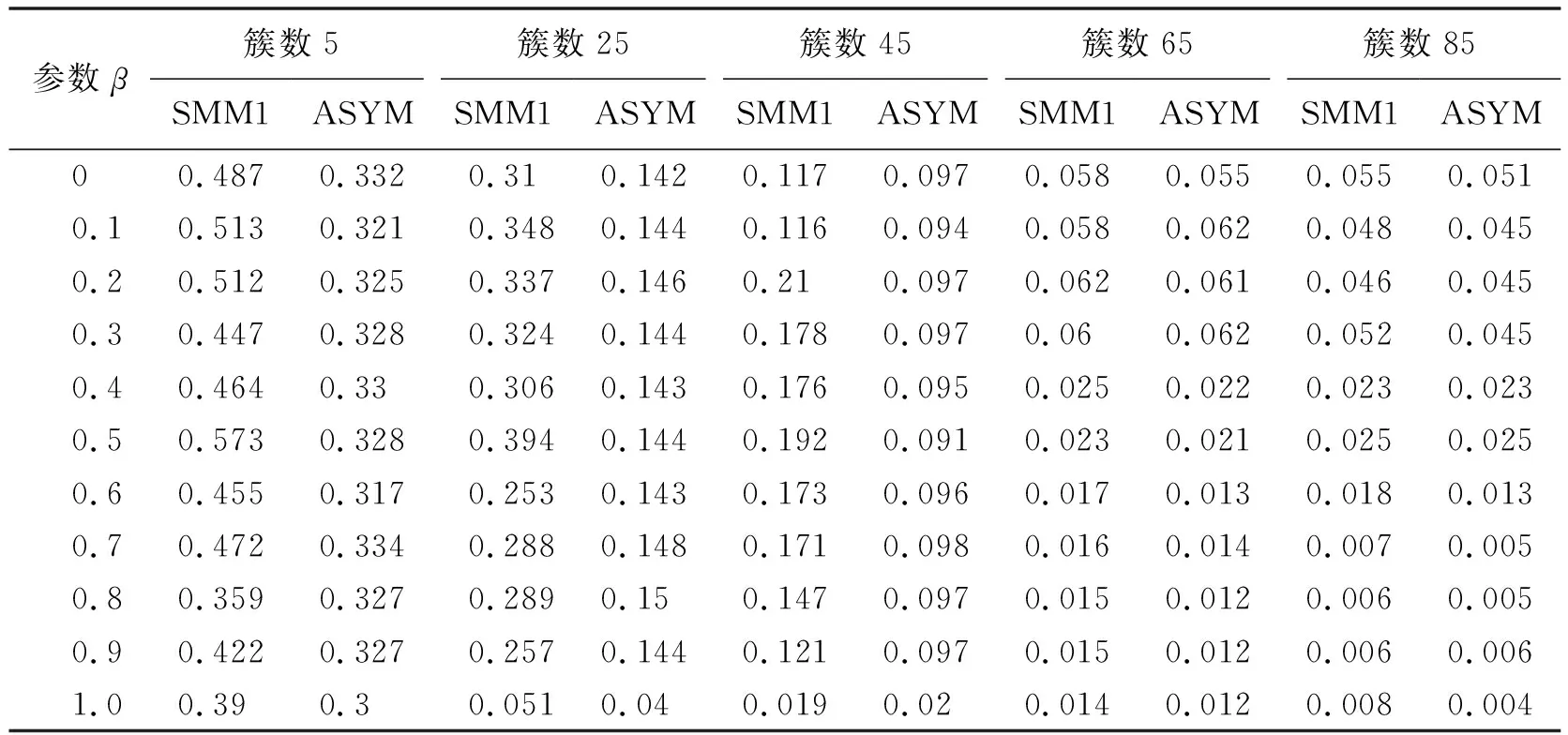
表6 不同β值SMM1方法和ASYM方法的平均熵值

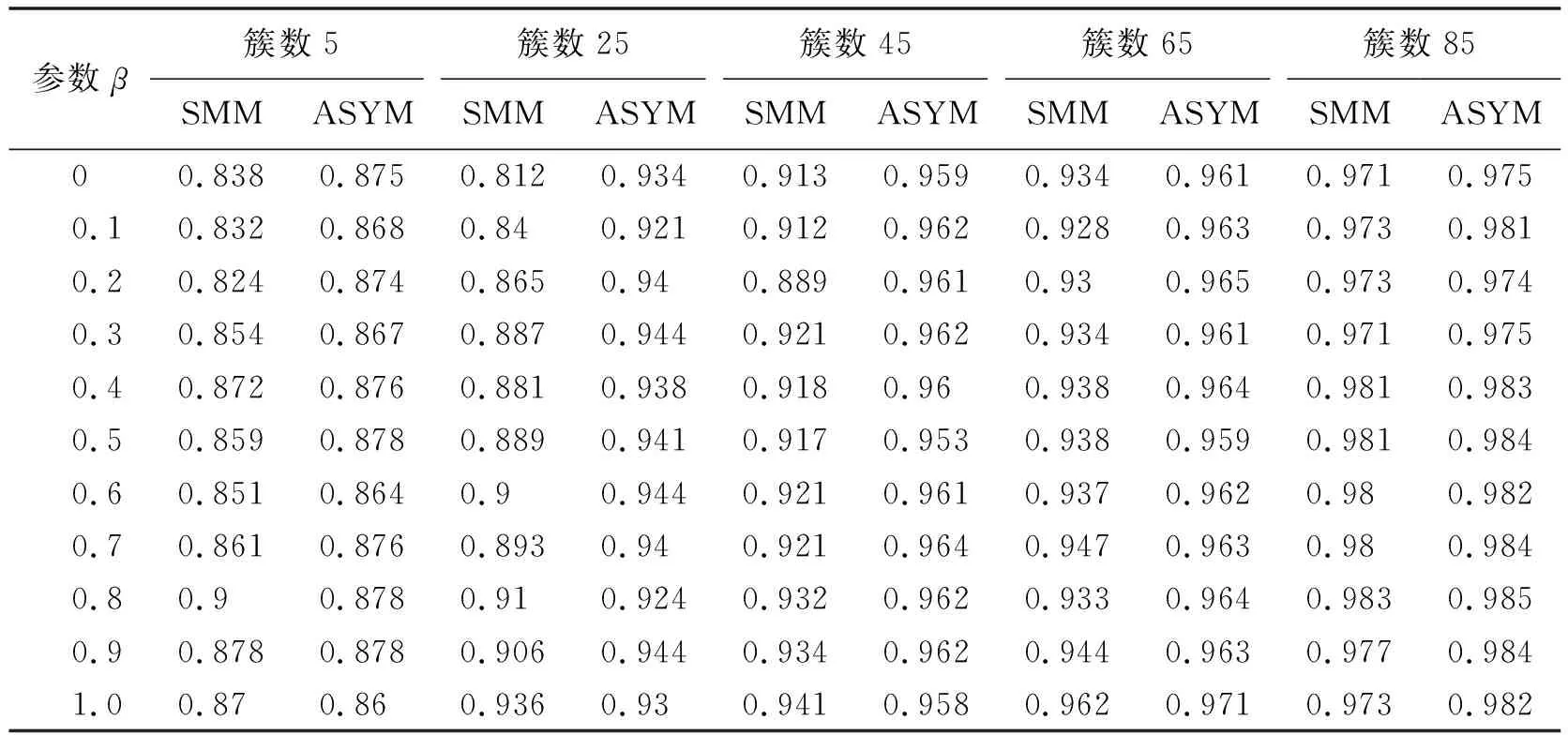
表7 不同β值SMM方法和ASYM方法的平均准确率

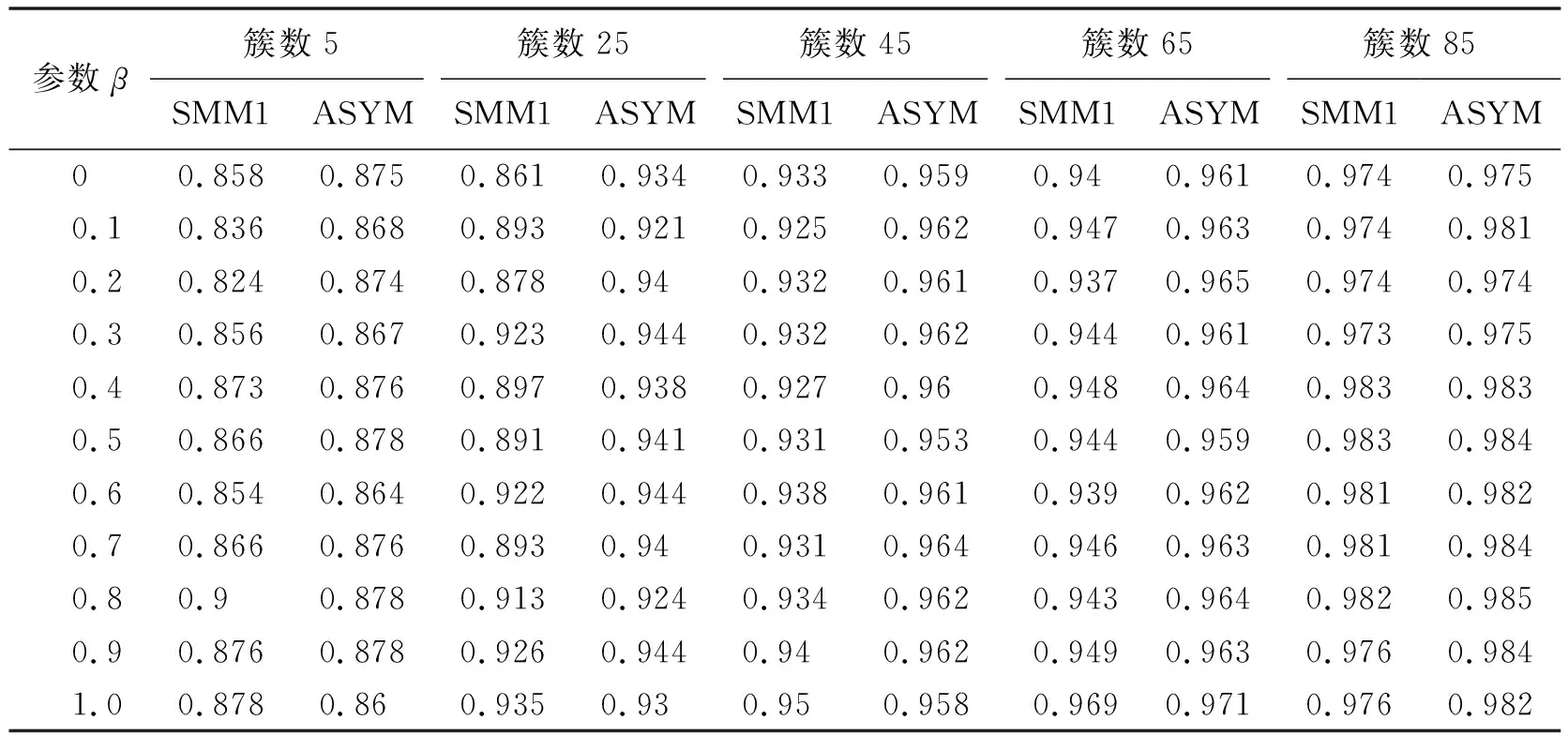
表8 不同β值SMM1方法和ASYM方法的平均准确率

由表5～8可知当β分别取0,0.1,0.2,…,1时，从5簇到85簇本文ASYM方法绝大多数的平均熵值低于SMM、SMM1方法的平均熵值，平均准确率高于SMM、SMM1方法的平均准确率.综合来看，本文ASYM方法进行聚类的效果优于SMM、SMM1两种对称方法.产生这种结果的原因是本文方法考虑了科技文档间关系的非对称性，能更准确地度量科技文档间关系，更好地区分了文档.例如任意2篇文档A、B，A是B的子文档，用对称方法聚类时，由于A、B相似，2篇文档会聚到同一簇中，但因为2篇文档关系是非对称的，有可能会聚到不同的簇，采用本文方法进行聚类会使聚类结果更准确.

进一步对表中数值进行观察和分析，可知当β=0.1时，ASYM方法的平均熵值比SMM方法的平均熵值最高降低了33%，平均准确率最高提高了8%.ASYM方法的平均熵值比SMM1方法的平均熵值最高降低了20%，平均准确率最高提高了4%.β=0.1且在不同结果簇数下，SMM、SMM1和ASYM方法的平均熵值和平均准确率对比如图3所示.由图3a可知，从65簇开始，随着簇数的增加，3种方法的平均熵值曲线趋于重合.而通过图3b可知在85簇时3种方法的平均准确率值趋于重合.

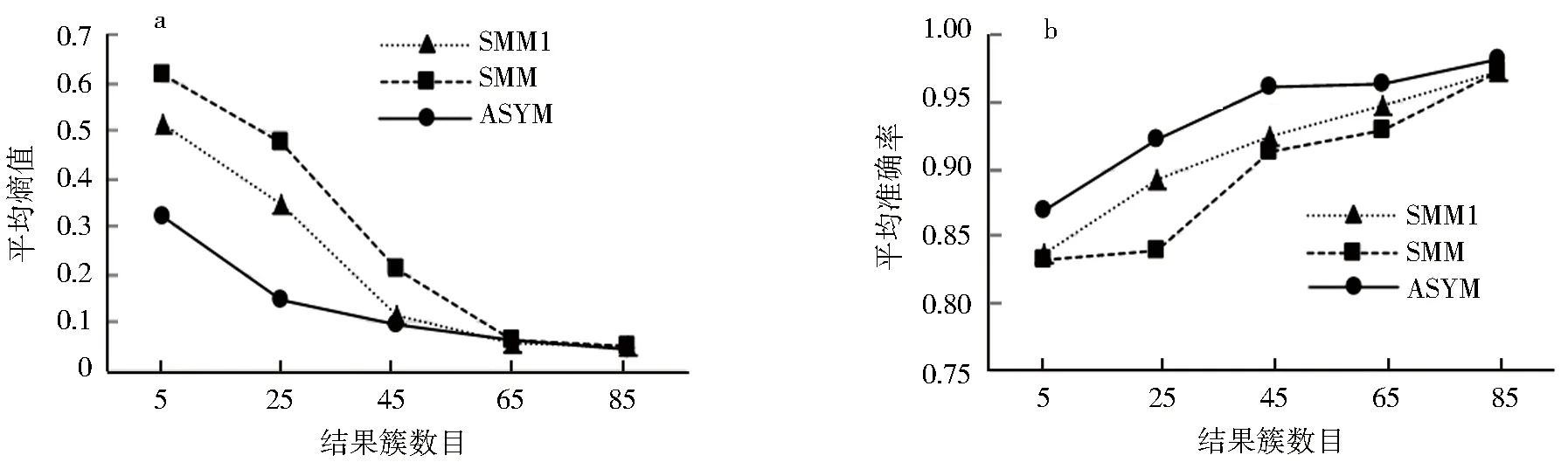
a.平均熵值对比；b.平均准确率对比.图3 SMM、SMM1、ASYM方法性能对比Fig.3 Performance comparison of SMM、SMM1、ASYM method

5 结语

科技文档间非对称关系可以更准确地反映文档间的相似程度.本文在分析科技文档间非对称关系的基础上，提出一种融合公式和文本的度量方法.实验结果表明：与SMM、SMM1两种方法相比，本文提出的ASYM方法的平均熵值有所降低，平均准确率有所提升.论文研究内容虽然取得了较好的效果，但尚有不足：1) ASYM方法仅考虑了科技文档中的公式和文本内容，并没有考虑图、表等信息，理论上，多维度内容的融合可以得到更好的度量效果；2)对于公式覆盖度的计算，论文仅将公式里的元素用一个集合表示，并没有考虑公式的位置因素、层次结构等，这些信息的考虑可以提高公式覆盖度计算的准确率；3)对于文本覆盖度的计算，论文主要依据了文本间的相对突出性，没有将语义信息融入其中.在未来研究中，将针对上述不足，对科技文档间的非对称关系展开更为深入的研究.