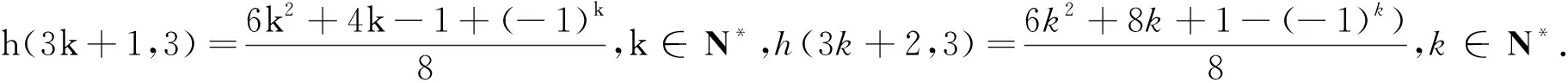分组、分配问题的递推公式及通项公式
张益明 (上海市奉贤中学 201499)
分组问题、分配问题是排列组合中非常重要的一类问题.通常该类问题只解决按照特定条件进行分组或分配的问题,比如:将4个不同元素平均分为两组,共有多少种不同方法?将4个相同元素分为两组,共有多少种不同方法?n个元素呢?很少有文章涉及这一问题,究其原因是情况较为复杂.本文将探究这类问题的递推公式及通项公式.
1 问题提出
(1)不同素分组问题:将n个不同元素分成m组,共有多少种方法?
(2)不同素分配问题:将n个不同元素分配给m个不同对象,共有多少种方法?
(3)同素分组问题:将n个相同元素分成m组,共有多少种方法?
(4)同素分配问题:将n个相同元素分配给m个不同对象,共有多少种方法?
分析若上述问题中的n,m比较小,则可以利用简单的排列组合知识加以解决.例如引文中提出的情况:n=4,m=2.

a1,a2-a3,a4;a1,a3-a2,a4;a1,a4-a2,a3;
a1-a2,a3,a4;a2-a1,a3,a4;a3-a1,a2,a4;a4-a1,a2,a3.
(2)因为n个元素各不相同,故只需将(1)中的分组进行排列即可,则方法数为7·2!=14种.
(3)将四个相同元素记为a,a,a,a,则分组方法仅有2种,即a-aaa,aa-aa.
(4)分配方法数有3种,即a-aaa,aaa-a,aa-aa.
但是若将问题变为一般的字母n,m,则问题变得异常复杂,本文将继续探寻此类问题的递推公式或通项公式.
2 问题解决
为了表达方便,将上述四个问题的答案分别用f(n,m),g(n,m),h(n,m),r(n,m)来表示.
2.1 问题(1)(2)的解决

下面用数学归纳法证明(*)式:
①n=2,m=2时,(*)式显然成立;
②假设n 即当n=k,m=s时,(*)式也成立.综上可知(*)式对于一切满足n≥m的自然数都成立. 第一步:给m组每组1个元素; 第二步:将剩余的n-m个元素分为1组、2组、…、min{n-m,m}组(每组至少一个元素),当n<2m时,h(n,m)=h(n-m,1)+h(n-m,2)+…+h(n-m,n-m). 又由n<2m,得n+1<2(m+1),则h(n+1,m+1)=h(n-m,1)+h(n-m,2)+…+h(n-m,n-m),两式相减有h(n,m)=h(n+1,m+1)(n<2m). ① 当n≥2m时,h(n,m)=h(n-m,1)+h(n-m,2)+…+h(n-m,m),又由n≥2m,得n-1≥2(m-1),则h(n-1,m-1)=h(n-m,1)+h(n-m,2)+…+h(n-m,m-1),两式相减有h(n,m)=h(n-1,m-1)+h(n-m,m)(n≥2m). ② 则①②即为同素分组问题的递推公式. 由①式得如下结论: h(3,2)=h(4,3)=…=h(m+1,m)=1,m≥2; h(5,3)=h(6,4)=…=h(m+2,m)=2,m≥3; h(7,4)=h(8,5)=…=h(m+3,m)=3,m≥4; h(9,5)=h(10,6)=…=h(m+4,m)=5,m≥5; …… 由②式有如下结论: 依此类推,可以得到h(n,4),h(n,5),…的通项公式,但是能否找到一个统一的式子还有待进一步研究.
2.2 问题(3)(4)的解决