面外弯曲加劲板结构受力特性探究

蔡军 安永日 李小斌

(1.青海省公路局，青海 西宁 810008；2.贵州大学土木工程学院，贵州 贵阳 550025；3.青海交通投资有限公司，青海 西宁 810008)

随着我国钢桥飞速发展，桥梁钢结构中曲线加劲板的应用越来越多。比如：主跨为550m的上海卢浦大桥、主跨为457m的柳州官塘大桥、主跨为420m的菜园坝长江大桥和主跨为450m的西江特大桥等。这些桥梁的拱肋采用了钢箱拱，拱肋加劲板和加劲肋均为曲线形状。另外，呼和浩特市南二环路部分立交工程、成都二环路部分匝道桥等，均采用了曲线钢箱梁，腹板和加劲肋向横桥向弯曲。

目前，国内外对弯曲钢结构构造的研究，主要集中于曲线加劲板-直线加劲肋结构，对加劲板和加劲肋共同弯曲桥梁结构的研究尚属空白。本文以菜园坝长江大桥钢箱拱肋顶、底加劲板为研究对象，利用ANSYS有限元软件分析了不同弯曲半径下的结构极限承载能力。分析结果表明，向面外凹曲加劲板承载力与直线加劲板基本相当，但向面外凸曲加劲板相比直线加劲板承载力小设计中不能忽略。同时，提出了曲线加劲板-曲线加劲肋结构的极限承载力计算公式，并与有限元分析结果作了对比，结果表明所提出公式的计算结果偏于保守。

一、极限承载力理论计算方法

弯曲半径R的加劲板结构在轴力N作用下受力模式如图1所示，在跨中存在初始挠度e0，并对截面产生附加弯矩。压弯构件的极限承载力可按式（1）式（2）计算：

图1 弯曲加劲板受力示意图

二、有限元分析模型

（一）构件基本构造

此次研究对象选用重庆菜园坝长江大桥，其桥型为主跨420m的组合式钢构系杆拱桥，拱肋为提篮式钢箱结构。拱轴线采用二次抛物线，计算矢高56.44m，矢跨比为1/5.67。拱肋截面如图2所示，钢箱拱肋横截面为矩形钢箱截面，高度为4m，宽度为2.4m，顶底板厚在24mm～40mm之间变化，加劲肋厚度在20mm～24mm之间变化。

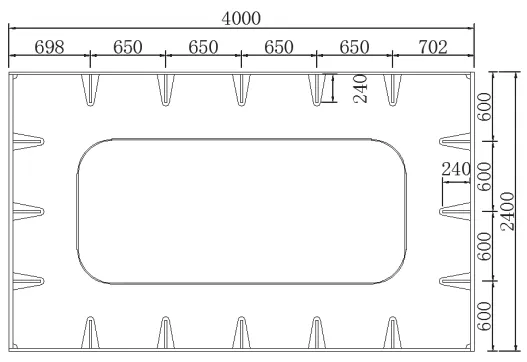
图2 钢箱拱肋尺寸(mm)

局部模型以菜园坝长江大桥钢箱拱肋顶板加劲板和底板加劲板为研究对象。为提高计算效率，拱轴线按圆弧线计算，计算长度取10m，将其作为基础计算模型，具体尺寸如表1所示。

表1 曲线加劲板基本参数（m）

表1中a、b、t分别为横隔板间距、母板宽度和厚度；hs、ts、ns分别为纵向加劲肋高度、厚度和数量；ht、tt、nt分别为横隔板高度、厚度和数量。

加劲板弯曲半径取值如表2所示，半径从∞～20m分6种，弯曲形状为向面外凸曲拱肋顶部加劲板和向面外凹曲拱肋底部加劲板。

表2 分析结构类型

（二）初始几何缺陷

图3 初始几何缺陷取值示意图

图4 残余应力场的简化计算模式（mm）

有限元计算模型中，初始几何缺陷如图3所示，取《钢结构设计规范》给定的最大幅值。焊接残余应力分布情况如图4所示，加劲板的残余拉应力为σy，残余压应力为0.25σy，加劲肋残余拉应力为σy，残余压应力为0.17σy 。

（三）有限元模型设计

拱肋加劲板、加劲肋、横隔板均采用Shell181单元。钢材应力—应变曲线如图5所示，屈服点为345.0MPa，弹性模量为2.06×105MPa，剪切模量为0.79×105MPa，切线模量为2.06×103MPa，泊松比为0.3。边界条件为约束母板四边竖向位移，约束所有横隔板底部径向位移，约束中间横隔板杆件方向位移和横向位移。加载方式为加劲板及加劲肋两端施加的均布线荷载，荷载增量采用弧长法。两种计算模型的具体边界条件及加载方式相同，如图6所示。

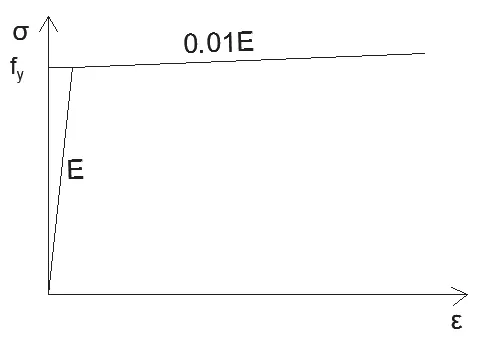
图5 材料本构关系

图6 数值分析模型示意图

三、有限元结果分析

（一）荷载—位移曲线及承载力

面外凸曲加劲板荷载—位移曲线如图7所示，半径越小初始刚度的降低越快，结构屈服点越低，与最大值及对应位移越小，荷载达到最大值后刚性下降越快。

面外凹曲加劲板荷载—位移曲线如图8所示，半径20m加劲板最大荷载明显比其他半径加劲板小，刚度降低、屈服点、最大值及对应位移等没有规律。

图7 面外凸曲加劲板荷载—位移曲线

图8 面外凹曲加劲板荷载—位移曲线

图9 面外凸曲加劲板最大荷载时等效应力云图（kPa）

表3 面外凸曲加劲板平均最大应力汇总结果

表4 面外凹曲加劲板平均最大应力汇总结果

面外凸曲加劲板平均最大应力汇总结构如表3所示，半径∞：320：220：140：80：20m的最大承载力比值为1.00：0.92：0.91：0.90：0.87：0.77，随着半径变小承载力下降，并降幅均超过5%设计中不能忽略。

面外凹曲加劲板平均最大应力汇总结构如表4所示，半径∞：320：220：140：80：20m的最大承载力比值为1.00：0.99：0.99：1.02：1.02：0.93，半径20m加劲板承载力降幅为7%，其他误差在2%以内，基本可不考虑弯曲影响。

（二）应力分布及变形

图10 面外凹曲加劲板最大荷载时等效应力云图（kPa）

面外凸曲加劲板的最大荷载时应力分布及变形如图9所示，除了加劲板与加劲肋连接处局部区域外其他区域都已经达到屈服状态。产生这种现象的原因在于此处由焊接而产生了初始拉应力。另外，由于硬化原因部分区域加劲肋等效应力超过屈服点，并已经发生面外屈曲。

面外凹曲加劲板的最大荷载时应力分布及变形如图10所示，半径80m～320m加劲板，除了加劲板与加劲肋连接处局部区域外其他区域都等效应力超过了屈服点。半径为20m的加劲板应力略小于屈服点，在横隔板处加劲肋等效应力超过了屈服点。

四、有限元分析结果与理论计算值对比分析

面外凸曲加劲板的有限元分析结果和理论计算值对比结果如表5所示，当弯曲半径∞～140m误差在5%以内，半径小于140m则误差偏大，并理论计算值偏于保守。产生这种现象主要原因在于压弯构件承载力相关计算公式为简化计算方法偏于保守。

面外凹曲加劲板的有限元分析结果和理论计算值对比结果如表6所示，理论计算值普遍大于有限元分析值，并误差较大。产生这种现象的主要原因在于压弯构件承载力相关计算公式偏于保守，并加劲板屈服后硬化原因等效应力已经超过了屈服值。

五、结语

本文通过弯曲半径∞～20m的面外凸曲和面外凹曲加劲板的有限元分析和理论计算值对比，得出了以下结论：

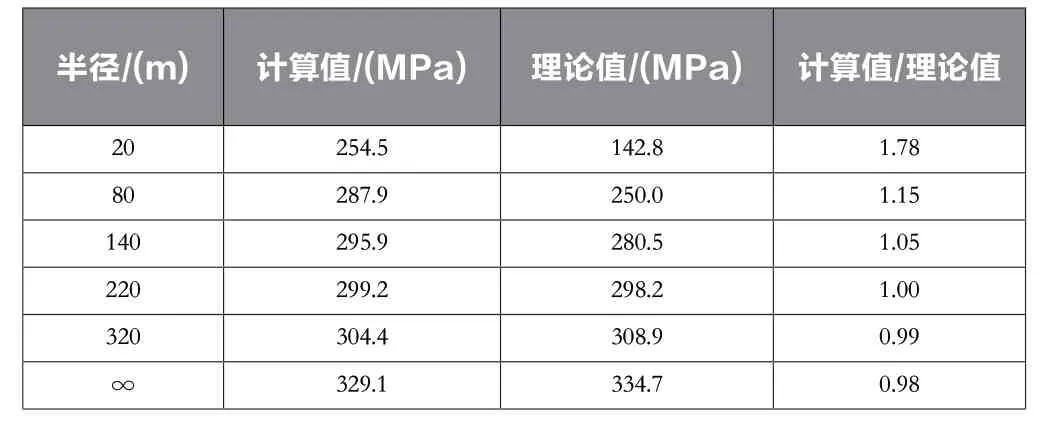
表5 面外凸曲加劲板最大应力计算结果

表6 面外凹曲加劲板最大应力计算结果

一是面外凸曲加劲板的承载力小于直线加劲板，半径越小降幅越大。在本文分析中弯曲半径320m～20m的降幅达到0.08～0.23，设计中不能忽略。

二是面外凹曲加劲板的承载力在弯曲半径320m～80m范围内，与直线加劲板相比误差在2%以内，基本可不考虑弯曲影响。

三是面外凹曲加劲板承载力比外凸曲加劲大，并随着半径减少差距变大。

四是本文中提出的理论计算方法偏于保守。