内压环索承网格结构张拉完成态稳定性分析及支撑方案优选

张宁远 罗 斌 张旻权 刘海霞

(1东南大学混凝土及预应力混凝土结构教育部实验室， 南京 211189)(2东南大学国家预应力工程技术研究中心， 南京 211189)

索承网格结构作为一种新型的刚柔杂交结构，由下部索杆系和上部刚性网格组成，下部索杆系可减轻结构自重，实现更大跨度，上部刚性网格便于屋面结构的安装.该结构目前已经广泛应用于大型体育场馆的建设中. 冯远等[1-3]对郑州奥体中心、徐州奥体中心等的索承网格结构进行了结构受力分析及找形研究，为索承网格结构的设计提供了参考；朱峰等[4-5]也对索承网格无支架施工方法进行了研究分析. 索承网格结构多采用外压环或上部刚性网格来平衡径向索索力，但当结构平面外形为非正圆形甚至存在直线边界时，会出现角部径向索索力过大[6]或压环受弯压力传递效率低等问题.内压环索承网格结构的压环位于上部刚性网格内部，不受结构外形的约束，曲率变化平缓，从而解决了角部径向索索力过大和压环受弯的问题. 径向索索力通过上部刚性网格中的径向主梁传递至内压环上，径向主梁受压存在一定的失稳风险.

屈曲分析是为了确定结构从稳定的平衡状态变为不稳定的平衡状态时的临界荷载和屈曲模态形状.目前，结构的屈曲分析主要包括特征值屈曲分析和非线性屈曲分析2种[7].Papadrakakis[8]将向量迭代方法应用至网壳结构稳定性分析中；冯若强等[9]对北京新机场航站楼的单层网壳结构进行了稳定性分析研究，结果表明考虑双非线性的铝合金网壳整体稳定承载力满足规范[10]的要求；刘璐等[11-12]通过无拉索和有拉索的单层柱面网壳模型试验发现拉索能提高结构的稳定承载力；Chen等[13-14]提出了群论方法，对空间预应力结构进行屈曲分析；张爵扬等[15]对不同初始缺陷分布和荷载工况下的双向悬索结构进行整体稳定性分析，发现结构对较小的初始缺陷并不敏感，较大的初始缺陷会使结构承载力显著降低；万宗帅等[16]进行了全跨和半跨雪荷载下充气式张弦穹顶的弹塑性稳定性分析，结果表明充气气囊可提高结构的整体稳定性，结构的失稳破坏形式为上弦杆件的塑性破坏.

本文以上海浦东足球场内压环索承网格结构为研究对象，建立了结构的有限元模型，对不同合龙方案及支撑组合下的结构张拉完成态结构进行了稳定性分析，包括特征值屈曲分析以及考虑几何非线性[17]和材料非线性的非线性屈曲分析.根据分析结果，选取合适的支撑方案，确保结构张拉完成态的稳定性.

1 工程背景

上海浦东足球场屋盖结构采用内压环轮辐式索承网格体系(见图1). 结构长轴长211 m，短轴长173 m，长轴向悬挑长度为47.2 m，短轴向悬挑长度为49.1 m，角部悬挑长度为56.3 m.径向索索力通过径向主梁传递至内压环，径向主梁处于受压状态. 径向索、径向主梁、内压环和V形撑形成预应力自平衡的主受力区域.

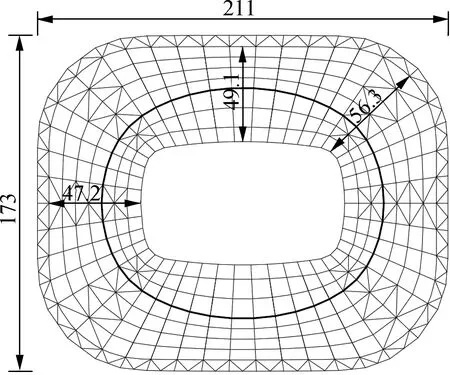
(a) 足球场屋盖平面尺寸图(单位：m)

内压环索承网格结构构件主要包括拉索和钢结构构件两大类. 其中，拉索包含46根径向索和8根环索，均采用密封钢绞线索，拉索规格见表 1.

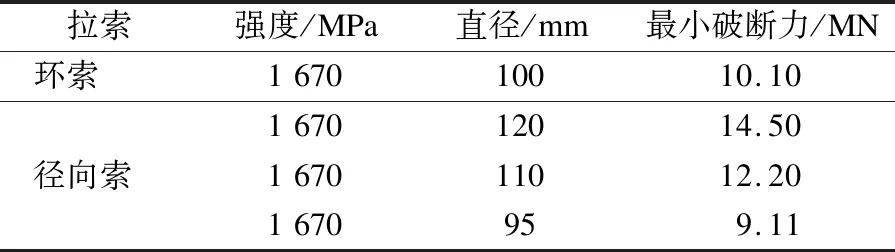
表1 拉索规格

钢结构采用Q345B型钢材.箱型截面构件的截面尺寸见表 2， 内设加劲肋以增强其稳定性.结构柱和柱间支撑采用圆管截面，截面尺寸分别为φ400 mm×10 mm和φ356 mm×10 mm.

表2 钢结构主要构件箱型截面尺寸

结构的施工过程如下：

①安装立柱并搭设场内支撑胎架，在立柱顶安装柱顶转换圈梁，在胎架上内压环梁.

②安装径向主梁、立柱外侧的悬挑梁部分、圈梁及V形撑外肢.

③提升环索，直至环索通过索夹与V形撑外肢连接.

④安装径向索并张拉，结构达到张拉完成态.

⑤安装合龙段钢结构、屋面支撑及内压环内侧悬挑网格部分钢结构.

⑥安装屋面檩条和马道，拆除胎架后安装屋面板，结构施工完成.

张拉完成态下结构存在一定的失稳风险，需要对结构的张拉完成态进行稳定分析.

2 张拉完成态稳定性分析

2.1 结构的有限元模型

根据设计单位提供的SAP2000有限元模型，在ANSYS软件中建立相应的结构有限元模型并分析计算，构件单元类型与SAP2000模型一致. 荷载条件为1.0倍结构自重+1.0倍恒荷载+1.0倍预应力，结果对比见表 3. 由表可知，总支座反力、径向索索力和环索索力的相对误差在0.5%以内，位移的最大误差值仅为-2.9 mm，钢构最大应力差值为-3.3 MPa，由此验证了本文模型的准确性和有效性.

表3 2种模型计算结果对比

2.2 支撑方案

为避免整个上部刚性网格参与受力，在上部网格设置合龙段. 合龙方案A为对称设置8个合龙段，方案B为对称设置4个合龙段，位于支撑胎架上的内压环梁始终保持连续封闭(见图 2).径向索张拉完成后，施工合龙段实现上部网格合龙. 支撑构件包括结构构件和临时构件，其中结构构件包括结构柱间支撑、外圈斜撑和屋面钢拉杆，临时构件包括临时柱间支撑和合龙段交叉斜撑.各支撑构件的布置位置见图3.不同合龙方案和支撑构件组合形成的9种支撑方案见表4.

(a) 方案A

(a) 柱间支撑设置位置

2.3 特征值屈曲分析

按照表4中不同支撑方案，各结构施工过程的非线性分析均收敛，达到正常的张拉完成态. 取张拉完成时的结构刚度作为特征值屈曲分析的计算刚度，对不同支撑方案下的张拉完成态进行特征值屈曲分析，得到其各阶屈曲特征值和模态，部分屈曲模态如图4～图7所示.各支撑方案的前6阶屈曲模态特征值见表5.

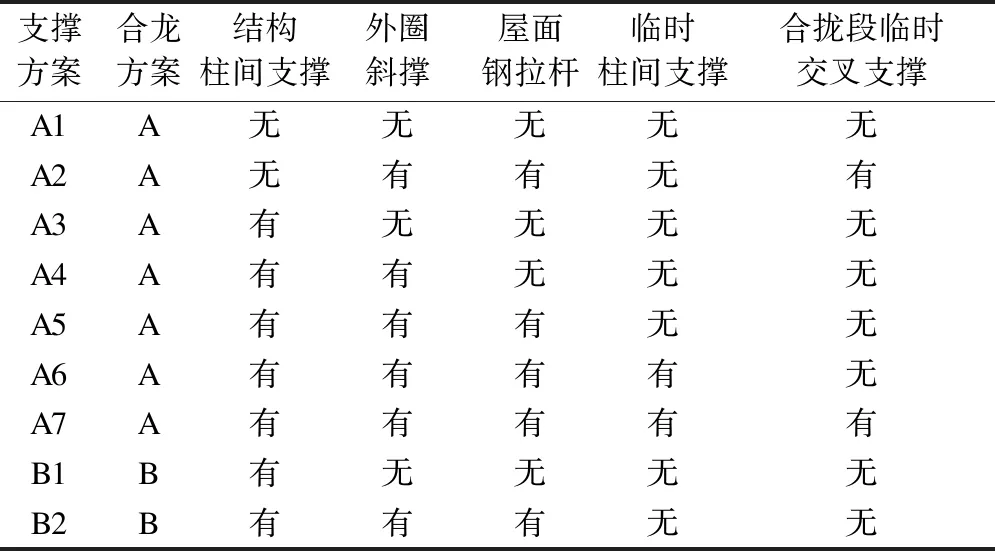
表4 支撑方案

表5 各支撑方案前6阶屈曲特征值

由图 4和图 5可知，结构低阶屈曲模态主要表现为结构扭转和长短轴径向位移相反. 支撑方案A1和A2均未设置柱间支撑，结构一阶屈曲模态为整体顺时针扭转，1阶屈曲特征值仅为0.001，结构稳定性差. 支撑方案A2较A1增设了屋面支撑，但结构稳定性没有得到显著提高.对比图 4和图 6可知，支撑方案A4设置了角部的结构柱间支撑，结构1阶屈曲模态为长短轴处的局部扭转，结构柱间支撑有效提高了结构的角部稳定性，采用支撑方案A4的结构1阶屈曲特征值为1.210. 由图 7(a)和(b)可知，支撑方案A6和A7设置了结构柱间支撑和临时柱间支撑，结构1阶屈曲模态均为长短轴径向位移相反，结构表现出良好的稳定性，1阶屈曲特征值分别为3.651和5.653. 由此可见，柱间支撑对结构稳定性的提高起着主导作用，有效减轻了结构的整体扭转和局部扭转.

(a) 1阶屈曲模态

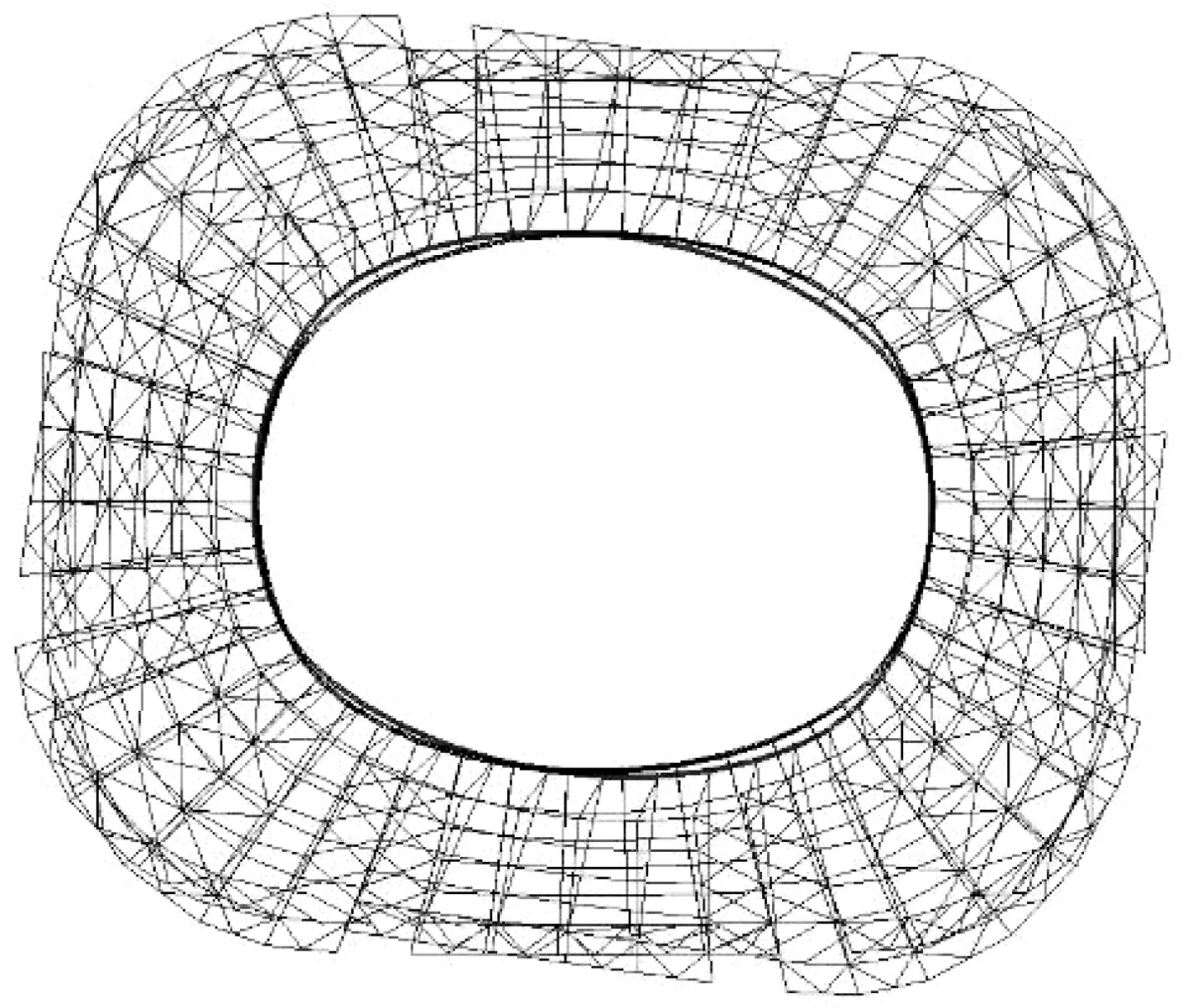
(a) 1阶屈曲模态

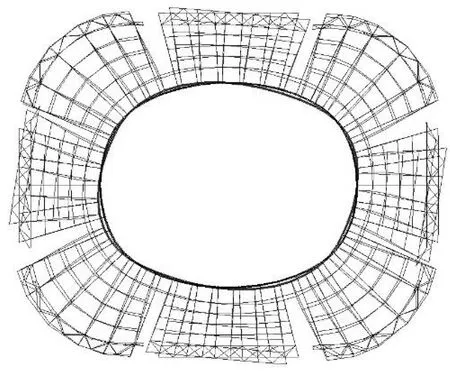
(a) 1阶屈曲模态

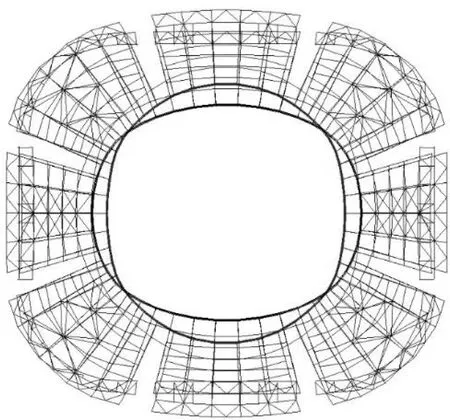
(a) 支撑方案A6

由此可知，支撑构件对提高结构张拉完成态稳定性的重要性由高到低依次为结构柱间支撑和临时柱间支撑、合龙段临时交叉支撑、屋面钢拉杆、外圈斜撑，因此柱间支撑为首选的支撑构件.通过对结构进行张拉完成态的线性屈曲分析可知，支撑方案A6、A7、B1、B2为保证结构张拉完成态稳定性的较优方案.

为进一步对支撑方案进行优选，对不同支撑方案下的结构成形态进行了计算分析，并与设计成形态的结构响应进行对比，结果见表6.由表可知，采用支撑方案A6和A7的结构响应与设计成形态的结果更为接近，采用支撑方案B1和B2的结构柱顶径向水平位移和上层网格竖向位移与设计成形态的结果相差较大，因此对采用支撑方案A6和A7的结构张拉完成态进行非线性屈曲分析.

表6 施工成形态与设计成形态结构关键参数对比

2.4 考虑几何非线性和材料非线性的非线性屈曲分析

考虑材料非线性和几何非线性，对采用支撑方案A6和A7的结构进行张拉完成态的稳定性分析计算.按《空间网格结构技术规程》(JGJ 7—2010)[10]中的规定，取最低阶屈曲模态为结构的初始缺陷，初始缺陷最大值按主梁最大跨度的1/300取值，即148.2 mm. 其中，钢结构采用Q345B型钢材，屈服强度为345 MPa，本构关系采用双折线模型，初始弹性模量为206 GPa，屈服后弹性模量为初始弹性模量的3%，即6.18 GPa. 拉索弹性模量为1.60 GPa，破坏时延伸率较小，没有明显的塑性平台，本构关系为线弹性. 结构张拉完成态的非线性稳定分析未考虑索破断力的影响. 荷载条件为拉索索力和结构自重. 在结构长轴、短轴及45°处分别设置内压环节点、径向梁跨中节点和柱顶节点，共计9个关键节点(见图 8).

图8 关键节点布置图

由图 9可知，考虑几何非线性和材料非线性时，荷载放大2.5倍后，节点位移迅速增大，与荷载放大倍数不再成线性关系. 此时，钢结构最大等效应力超出材料屈服强度，部分构件进入塑性状态，结构稳定性丧失. 采用支撑方案A6的结构安全系数为2.5，高于《空间网格结构技术规程》(JGJ 7—2010)[10]中规定的安全系数2.0. 由图10可知，采用支撑方案A7的结构，在荷载放大3.0倍后，节点位移与荷载放大倍数不再成线性关系，结构稳定性丧失. 结构安全系数为3.0， 同样高于规范要求的2.0，结构失稳模式与支撑方案A6相似. 与支撑组合A6相比，采用支撑方案A7的结构节点位移和增长速率明显降低，说明合龙段临时交叉支撑的设置有效提高了结构的整体性和稳定性，从而使结构位移显著降低.若考虑索体破断，径向索和环索索力在放大至2.8倍时，索力达到索的最小破断力，从而发生断裂破坏，结构丧失承载力.支撑方案A6和A7的结构安全系数均能满足《空间网格结构技术规程》(JGJ 7—2010)[10]的要求.与支撑方案A6相比，支撑方案A7需增设合龙段临时交叉支撑，从而增加了施工难度. 根据分析结果可知，采用支撑方案A6作为结构张拉施工过程中的支撑方案更为合理经济，即在结构张拉施工之前安装结构柱间支撑、临时柱间支撑、外圈斜撑和屋面钢拉杆在内的支撑构件.

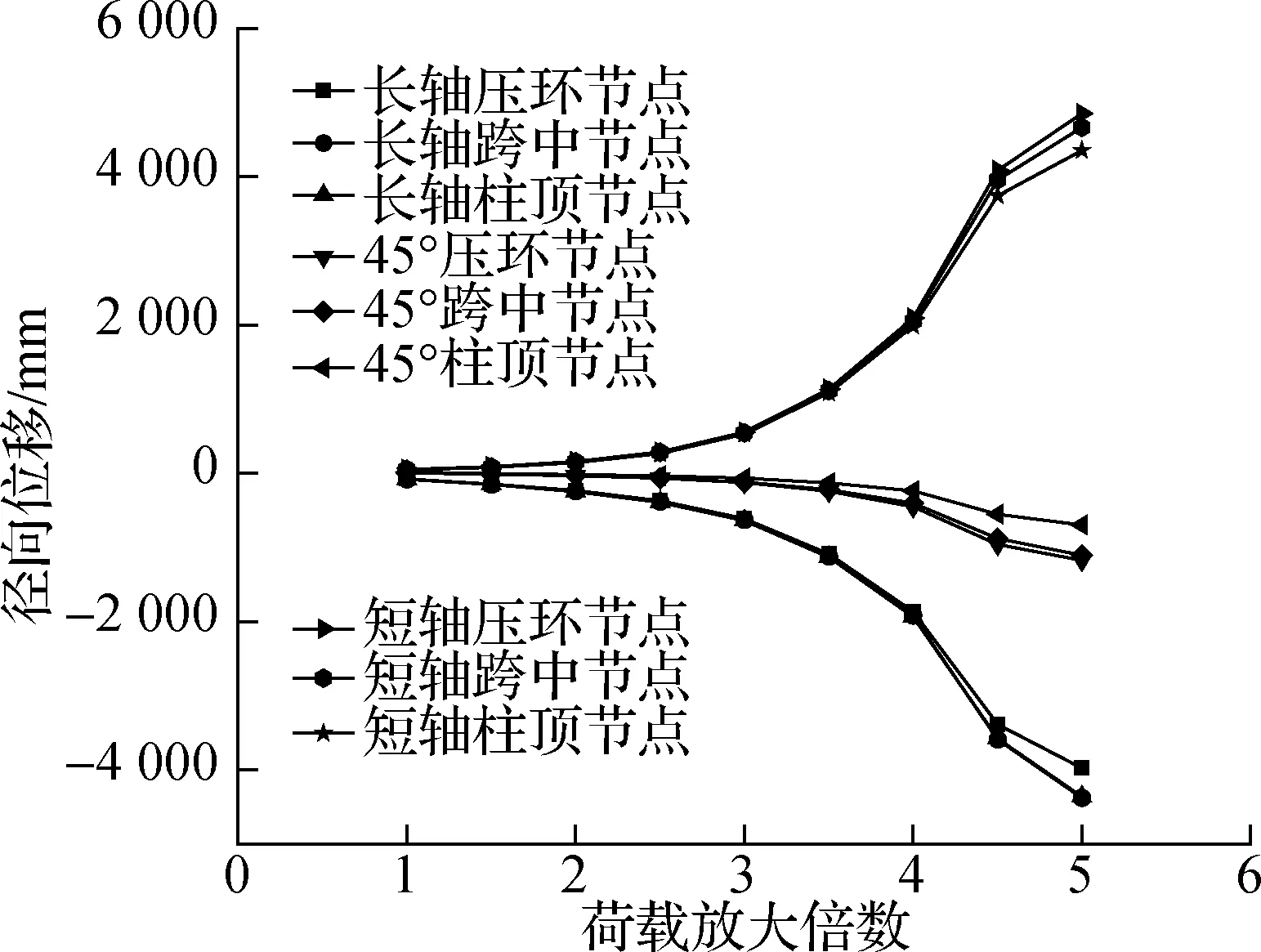
(a) 径向位移

(a) 径向位移

3 结论

1) 未设置柱间支撑的情况下，内压环索承网格结构在张拉完成态下极易发生结构整体顺时针扭转，结构一阶屈曲特征值为0.001.

2) 结构柱间支撑和临时柱间支撑能够显著提高结构在张拉完成态的稳定性.减少合龙段数量可以提高结构张拉完成态下的稳定性，但施工完成后的结构位形与设计位形存在一定的偏差.

3) 考虑几何非线性和材料非线性，采用支撑方案A6和A7的结构安全系数分别为2.5和3.0，均能够满足规范要求的2.0.为降低施工复杂程度，选择支撑构件较少的A6作为结构支撑方案.

4) 非线性屈曲分析中，拉索索力达到最小破断力，导致结构破坏可能早于结构失稳发生.