考虑绿波控制的双相位移位左转交叉口效用分析

徐良杰 朱然博 陈国俊 王 涛 李 福

(1武汉理工大学交通学院, 武汉 430063)(2湖北文理学院汽车与交通工程学院, 襄阳 441053)

平面交叉口的左转车流是影响对向直行车流通行、产生车流冲突的关键车流.因此,为提高交叉口最大通行能力,国内外学者提出了一些非常规的交叉口,其中移位左转(CFI)设计交通干扰小、效益高[1].对比其他类型的设计而言,在缩减信号周期、减少相位数、降低车均延误方面具有明显优势[2-3],是当前研究的热点方向.

在移位左转交叉口渠化设计方面,Inman[4]选取101名参与者,利用驾驶模拟器来对比评估3种不同导航标志方案在移位左转交叉口的使用效果,实验结果表明3种方案的实施效果类似,均能使第1次面对移位左转的参与者顺利通过交叉口.Ladda等[5]和钱萍等[6]分别用VISSIM仿真和建模的方式探究了移位左转储存道长度与通行能力、信号周期等的关系.Yang等[7]以最大排队长度与可用车道长度的比率作为关键变量,通过对比其与各临界点下延误之间的关系,进而建立了移位左转交叉口几何设计规划模型.

在移位左转交叉口信号控制方面,Hatem等[8]通过VISSIM仿真对比了常规路口和移位左转交叉口在通行能力、饱和度与总延误等方面的差异,但未提出信号控制模型.常云涛等[9]以延误最小为目标函数建立了移位左转交叉口信号配时优化模型,但未考虑交叉口渠化设计对信号配时的影响.因此,国内外学者[10-13]综合考虑交叉口渠化与信号控制中各个参数,针对各类型的移位左转交叉口设计了相应的渠化信控模型,并用仿真验证其有效性.

综上,移位左转通过减少相位相序和冲突点数,优化交通组织来提升交叉口通行能力,但直行车在交叉口处的偏移问题、移位左转的延误计算问题和2次停车问题等仍亟待解决.因此,本文综合考虑移位左转交叉口渠化与信号控制中各参数之间的复杂关系,建立了考虑绿波控制的双相位移位左转交叉口模型,以最大程度上提升移位左转交叉口的通行效率.

1 移位左转交叉口渠化模型

移位左转交叉口的设计如图1所示[2],其将左转车道移至对向的出口道外侧,使得左转车流在路段交叉口处提前驶入移位左转车道,进而消除左转车流与对向直行车流在主交叉口处的冲突,使对向左转和直行车流在交叉口信号灯的控制下可以同时通过交叉口.

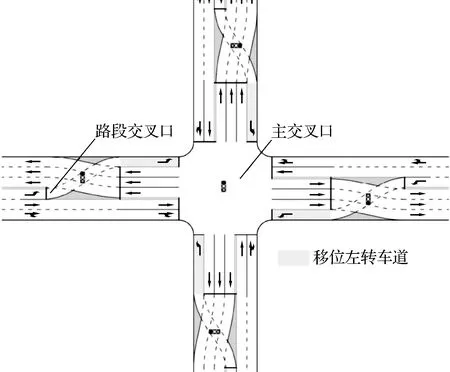
图1 移位左转交叉口

由于国内右转车流在交叉口处可以直接驶入出口道的外侧车道,不受信号灯控制,而移位左转将左转车道移至出口道外侧,占用了右转车流的通行空间,导致左转车流与右转车流发生冲突.同时,该方案的交通组织较为新颖,驾驶员对移位左转不太熟悉,导致交叉口交通事故发生频繁[14].因此本文采取拓宽交叉口进口道和出口道的方式,通过设置右转专用车道以避免移位左转车流与右转车流的冲突,具体渠化方案与车流组织如图2所示,图中①～④为车流行驶路线编号.

据此设计的移位左转交叉口渠化方案与车流行驶规则如下：

1) 本文根据移位左转交叉口的特点,分别对进、出口道的拓宽方案进行设计.进口道右转的展宽渐变段lyd与展宽段lya根据《城市道路交叉口规划规范》(GB 50647—2011)进行计算.出口道右转的展宽渐变段lzd根据规范计算,展宽段lza需根据移位左转储存道的长度l1进行计算.为保证东西方向的右转车流不会与南北方向的左转车流发生冲突,展宽段的长度lza需大于移位左转储存道的长度l1,即lz≥l1.

2) 在图2的交叉口中,南北方向设置移位左转车道,东西方向无左转车流,不设移位左转车道.南北方向的左转车流根据预信号提示,沿路径②提前驶入移位左转储存道中等待通行.当南北直行绿灯启亮时,直行车流沿路径①先向交叉口中心位置偏移一个车道驶入进口道,然后直行驶出交叉口,左转车辆沿路径②驶出交叉口.南北与东西方向的右转车流分别沿路径③和④驶入相应的出口道,不受信号灯控制.该方案较传统移位左转交叉口,直行车流的偏移地点由交叉口处提前至路段中部,由车道线辅助驾驶员行驶,使车流可直行通过交叉口,以减少事故的发生.同时,在保证交叉口通行能力的前提下,南北方向的人行横道长度由原来的六车道变为五车道,减少行人过街时间.

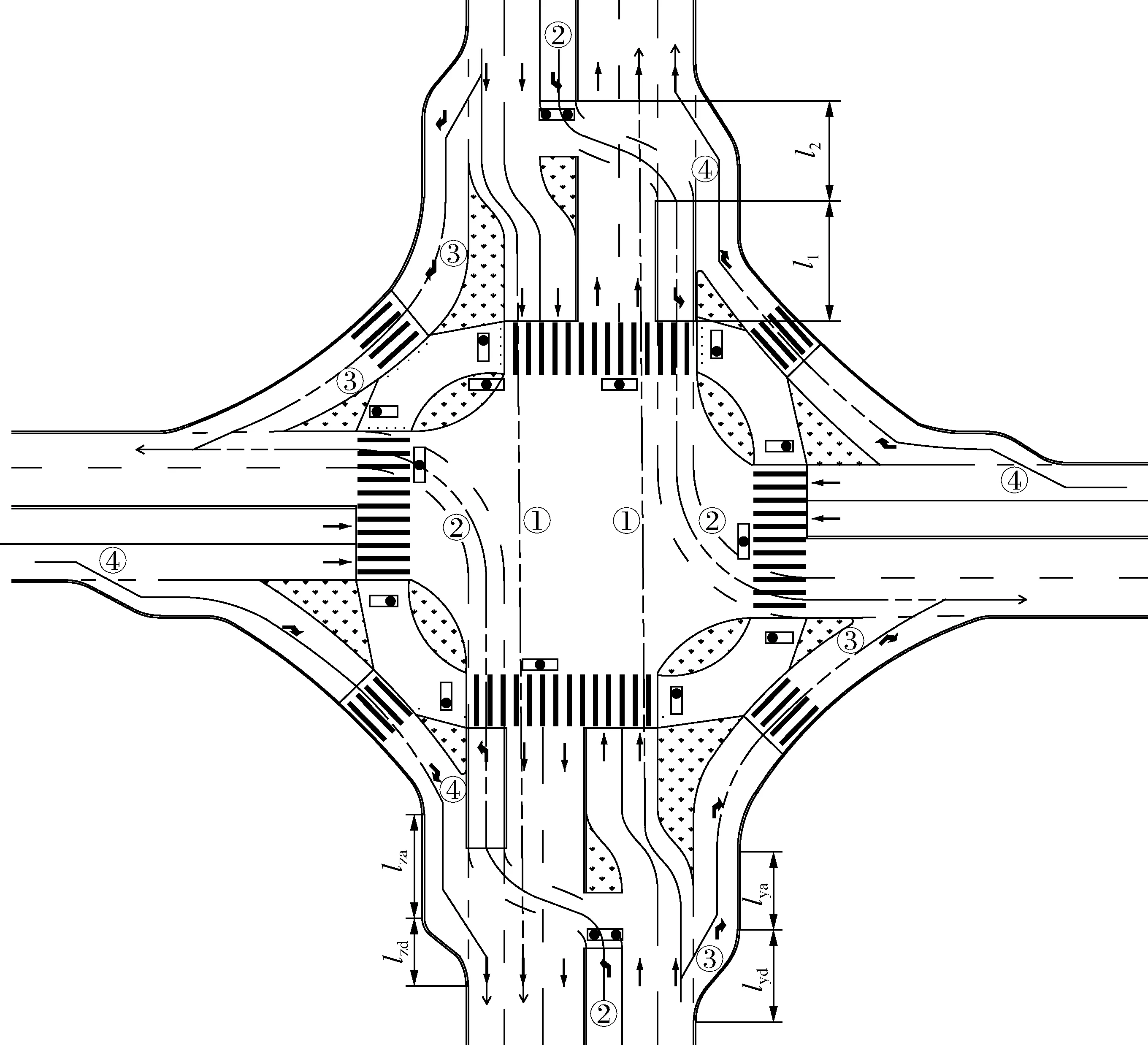
图2 移位左转交叉口渠化方案图

3) 若交叉口某方向设置了移位左转,为避免对上游交叉口产生影响,交叉口该方向距上游交叉口的距离ls应大于等于移位左转储存道长度、路段左转变道长度和路段左转车流排队长度之和,即

(1)

式中,l2为路段左转变道长度,m；q为左转车流量,pcu/h；C为交叉口信号周期,s；hs为平均车头间距,m；ny为移位左转车道数；PHF为高峰小时系数.

因此该移位左转方案适用于双向四车道及以上、与上游交叉口相距较远、南北(东西)方向的左转车流较大的情况,当东西(南北)的左转车流较小时可采用禁止左转的措施,且非机动车道或人行道较宽时,可进一步拓宽进出口的机动车道的交叉口.

2 考虑绿波控制的双相位移位左转交叉口信控优化模型

2.1 目标函数

由于本方案对交叉口的进、出口道进行拓宽,右转车辆可以不受信号控制直接驶入相应出口道,因此以交叉口直行与左转车流的车均延误最小为目标函数,不计算右转车流的车均延误.优化目标函数如下：

(2)

式中,dz为交叉口直行与左转车流的车均延误,s；i=1,2,…,6分别表示东、南、西、北直行、南、北左转的车流；Di为各方向的车均延误,s；qi为各方向的车流量,pcu/h.

2.2 相位相序设计

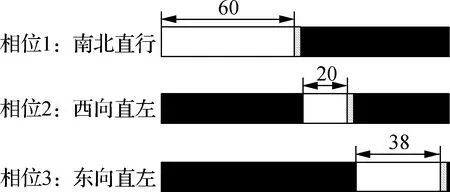
本文以南北方向设置移位左转为例进行说明,东西方向仅存在直行与右转车流.若南北主交叉口的直行与左转信号为相位1,则东西直行信号为相位2.当东西方向直行绿灯启亮时,主交叉口的交通信号需与路段左转变道预信号相协调,让南北方向左转车流进入移位左转储存道中等待.本文信号配时与相位相序设计方案如图3和图4所示.图中,g1为相位1绿灯持续时间；g2为相位2绿灯持续时间；gy为预信号绿灯持续时间；ty为路段预信号绿灯启亮时间与相位2绿灯启亮时间的相位差.

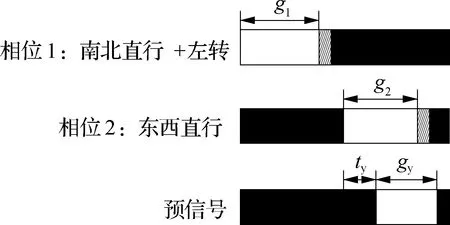
图3 信号配时设计方案

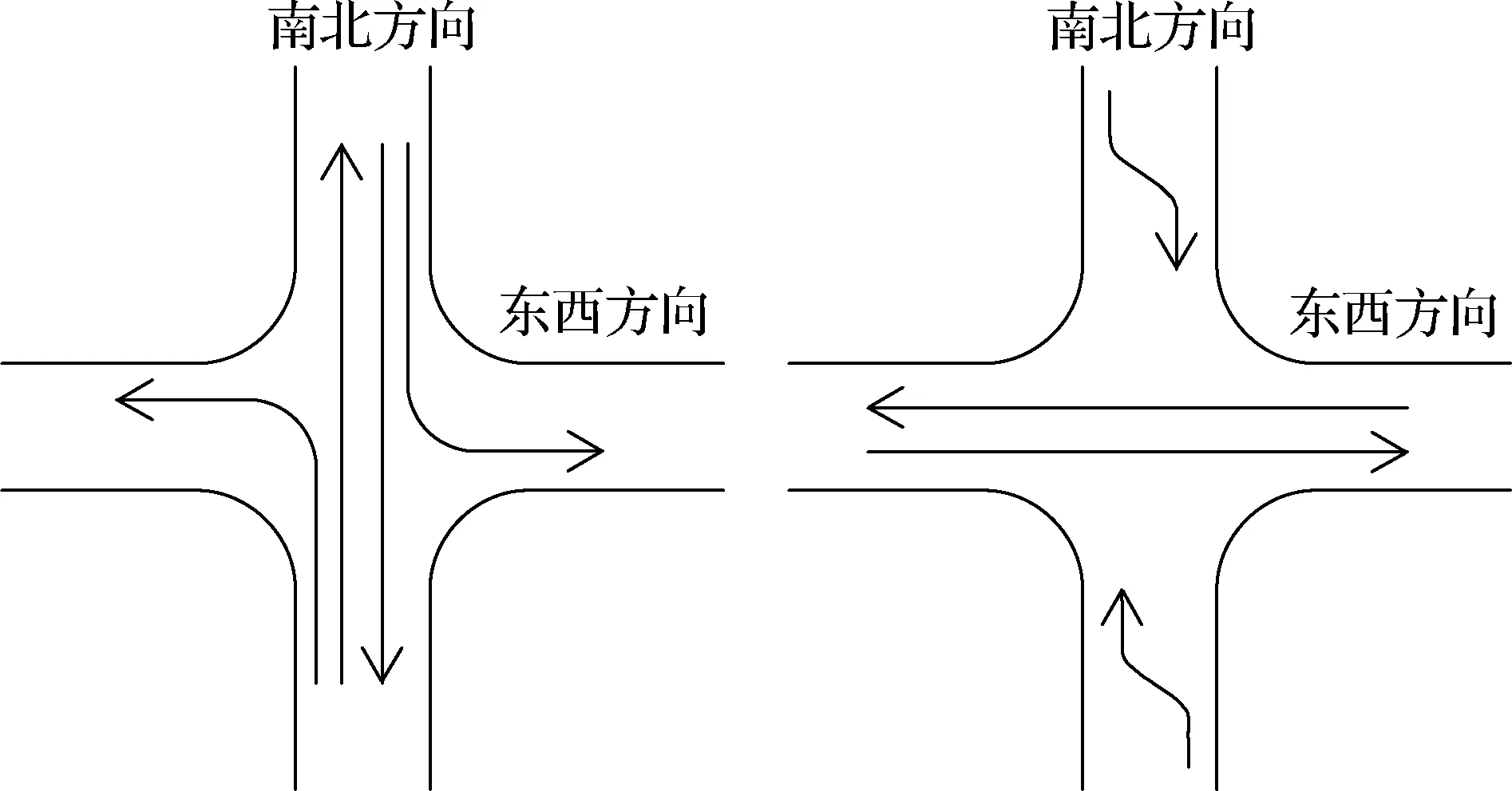
图4 交叉口信号相位相序设计方案

2.3 约束条件

2.3.1 各相位有效绿灯时长计算

各相位有效绿灯时长应使一个周期内到达的车辆数全部驶出交叉口而不发生溢流.本文基于交通流疏散波理论,分别计算相位1直行与左转车辆的排队消散时间t1与最后一辆车从启动到通过交叉口的时间t2.由于相位1为交叉口直行与左转相位,因此

(3)

(4)

式中,ni为各方向的车道数；v1为车队直行的平均速度,m/s；v2为车辆直行的平均速度,m/s；v3为车队左转的平均速度,m/s；v4为车辆左转的平均速度,m/s.

则相位1的绿灯持续时间g1为

g1≥t1+t2

(5)

同理,相位2的绿灯持续时间g2及预信号的绿灯持续时间gy为

(6)

(7)

因此,信号周期时长为

C=g1+g2+L

(8)

式中,td为车辆平均启动延误,s；L为信号周期总损失时间,s.

2.3.2 移位左转储存道长度l1计算

左转车辆需在路段停车,在信号控制下进入移位左转车储存道.移位左转储存道的长度与交叉口左转小时交通量及预信号持续时间有关,同时考虑到高峰时期左转交通量的突然增加,移位左转储存道的长度还与高峰小时系数有关,且通常情况下,移位左转储存道的长度不大于100 m[12,15].因此l1应满足

(9)

(10)

l1≤100

(11)

2.3.3 路段左转变道长度l2计算

左转车辆需在路段停车,在信号控制下进入移位左转车储存道,该路程的纵向长度即为路段左转车辆变道长度,如图5所示.其表达式为[12]

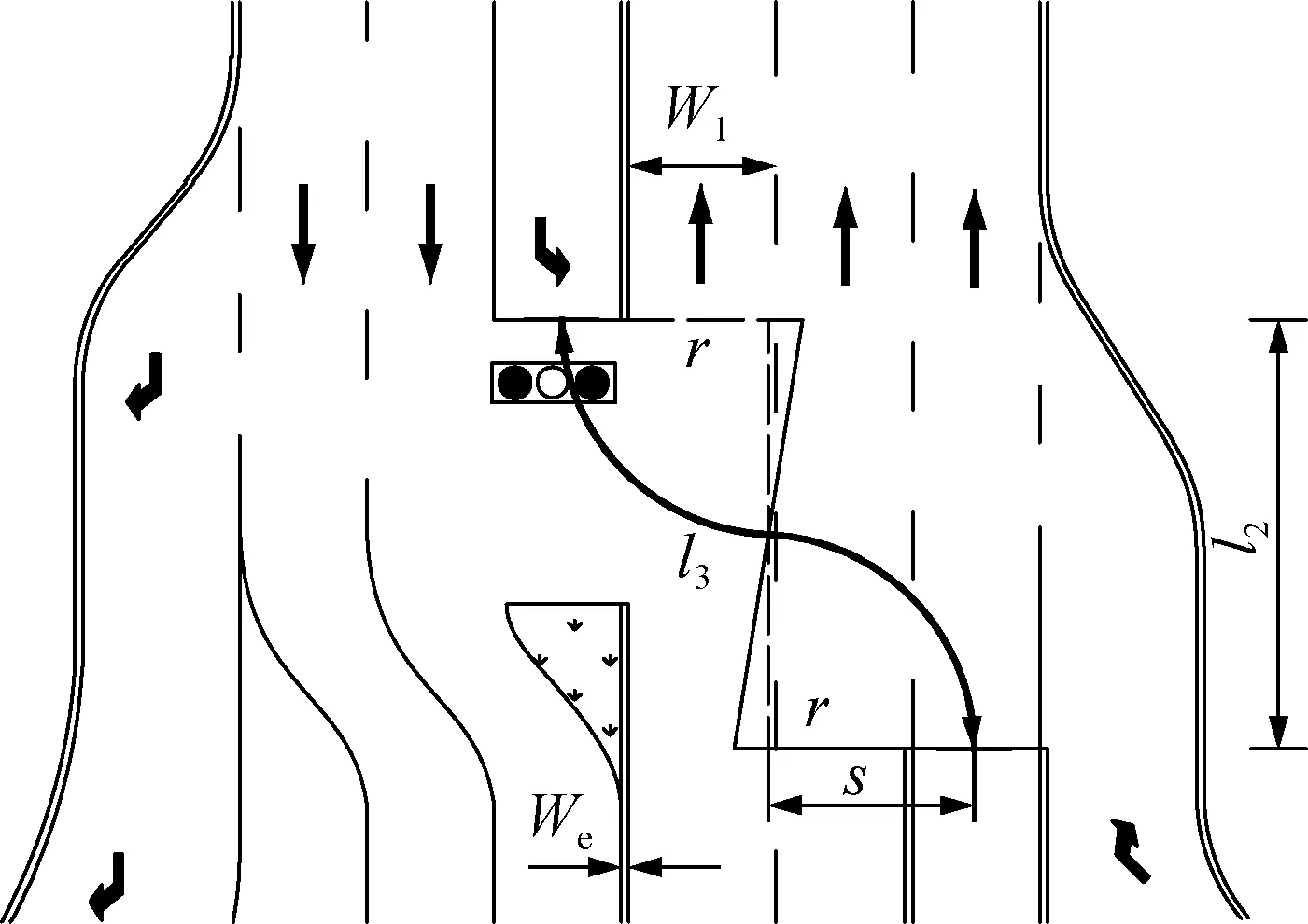
图5 长度计算图

(12)

式中,r为车辆最小转弯半径,m；s为几何计算的中间变量,m；W1为一条车道的宽度,m；We为双黄线宽度,m.

2.3.4 路段左转行驶路径长度l3计算

左转车辆在路段交叉口进入移位左转储存道的路程长为l3,由2段相等的圆弧组成,如图5所示,则有

(13)

2.3.5 基于绿波控制的预信号约束条件

为减少移位左转车辆的停车次数,保障车辆的行驶安全,结合绿波控制理论构建如下约束条件：

1) 交叉口相位1为南北的直行与左转信号,为保证该相位的左转车流全部顺利通过交叉口,应使路段交叉口的预信号持续时间不大于主交叉口的相位1绿灯持续时间.

2) 为保证路段交叉口的运行安全,应确保上一相位南北直行车辆顺利通过路段左转交叉口处,使得路段交叉口左转车辆可以顺利进入移位左转储存道,因此预信号的启亮时间应延迟至南北直行的最后一辆车驶离路段交叉口时.

3) 由于预信号启亮时间需延迟,可能会导致路段左转最后一辆车与南北直行车辆产生冲突,因此需确保南北直行车辆到达路段交叉口时,路段左转的最后一辆车抵达移位左转储存道尾端.

4) 为保证交叉口通行效率,由于移位左转设计方案中左转车流需分别在路段交叉口与主交叉口进行2次停车等待绿灯放行,因此可将路段交叉口的绿灯启亮时间与主交叉口的绿灯启亮时间协调控制,使第1辆左转车辆驶出路段交叉口到达主交叉口时,主交叉口的绿灯同时启亮,以减少左转车辆的延误.

5) 当相位2东西方向直行信号结束时,下一相位南北方向直行车流到达路段交叉口处尚需一定的时间,因此路段交叉口预信号的结束时间可以比相位2东西直行信号的结束时间晚.

上述条件可表示为

gy≤g1

(14)

(15)

(16)

(17)

gy≤g2+L2

(18)

g1≥g1min

(19)

g2≥g2min

(20)

式中,l4为南北直行车辆从主交叉口停车线到相应出口道的距离,m；v5为左转车辆在移位左转储存道内直行的平均速度,m/s；L2为相位2的信号损失时间,s；g1min,g2min为相位1和相位2满足行人过街的最短绿灯时间,s.

2.4 移位左转交叉口车均延误模型

本文基于上述交叉口渠化方案,建立移位左转交叉口的延误计算模型,假设如下：

1) 交叉口渠化方案如图2所示.南北方向设移位左转车道,东西方向无左转车辆,交叉口相位相序图如图3和图4所示.

2) 交叉口各进口道车辆到达服从泊松分布,所有右转车辆从右转专用道驶离交叉口,对直行与左转车辆干扰较小.

3) 不考虑行人与非机动车对交叉口的干扰.

2.4.1 东西直行相位的车均延误

东西直行相位不受移位左转车道的影响,其车均延误的计算与传统交叉口相同,本文采用参数标定后的HCM2010延误模型[16]进行计算：

(21)

式中,xi为各方向对应相位的饱和度；T为分析持续时间,s；ci为各方向对应相位的通行能力,pcu/h.

2.4.2 南北直行相位的车均延误

南北直行相位受移位左转车道的影响,因此该相位的延误由直行车与左转车的延误组成.直行车的延误不受移位左转车道影响,其延误按式(21)计算得到.左转车需先在路段交叉口等待预信号绿灯进入移位左转储存道,该方式与正常交叉口基本一致,即

(22)

式中,Dy为移位左转车流在路段交叉口的车均延误,s；xy为预信号相位的饱和度；cy为预信号相位的通行能力,pcu/h.

由于本文移位左转方案对路段交叉口的绿灯启亮时间与主交叉口的绿灯启亮时间协调控制,使得第1辆左转车辆驶出路段交叉口到达主交叉口时,主交叉口的绿灯同时启亮.因此左转车辆在移位左转储存道内无停车延误.由于车辆会产生排队现象,因此需计算左转车流在移位左转车道内的车均排队消散延误Dp,即

(23)

式中,vf为排队疏散波波速,m/s.

因此南北移位左转车辆的车均总延误为

Di=Dy+Dpi=5,6

(24)

3 仿真评价

3.1 移位左转方案效用分析

3.1.1 单移位左转车道效用分析

虽然移位左转方案能够改善交叉口通行能力,降低交叉口车均延误,但该方案建设工期长,造价成本较高[1],因此需探究交叉口在何种条件下适用于移位左转方案.本文通过调整交叉口饱和度,使饱和度x=0.5,0.6,…,1时,得到交叉口的总车均延误与左转车均延误,如图6所示.

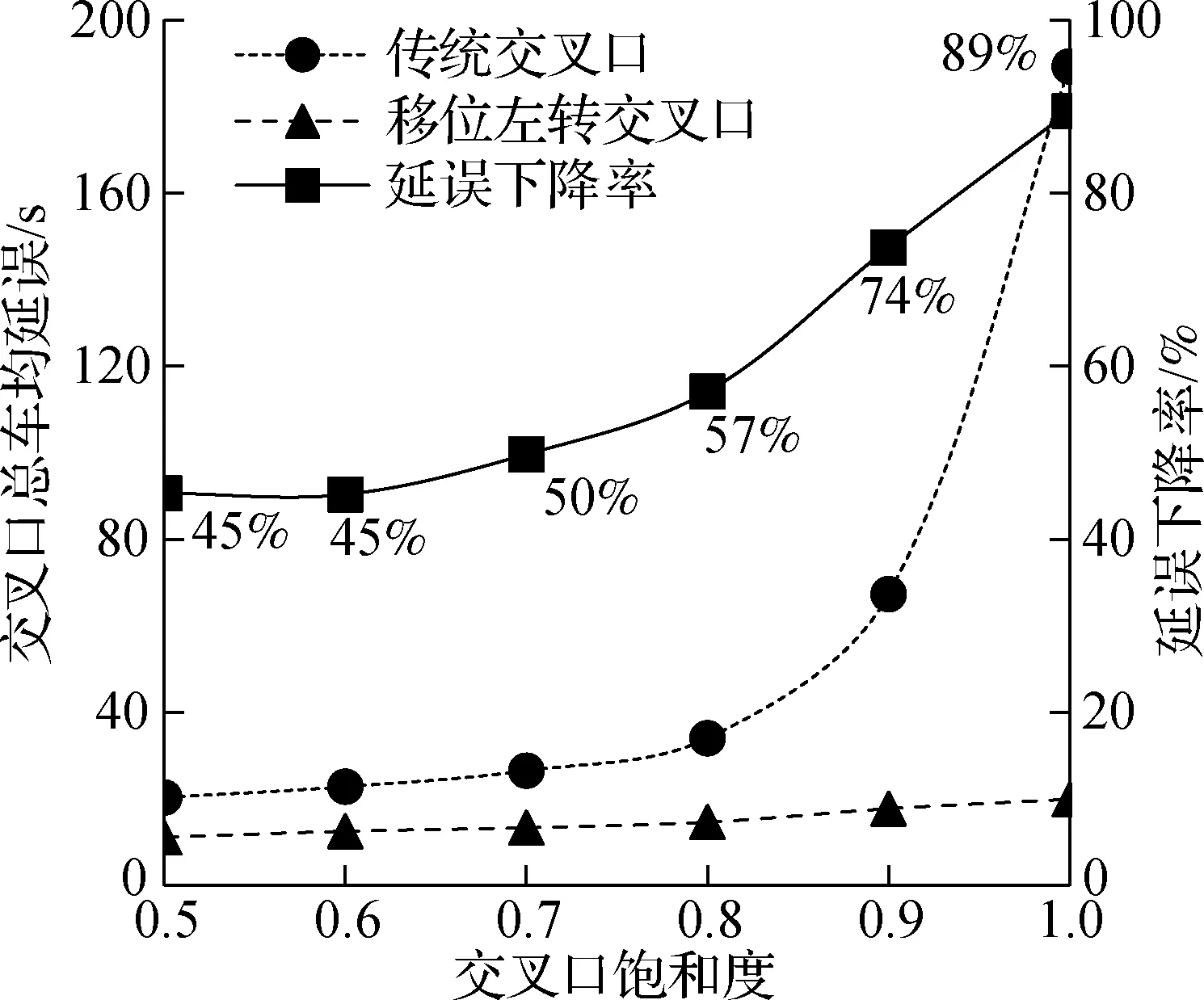
(a) 交叉口总车均延误

由图6分析可得,当交叉口饱和度小于0.8时,移位左转交叉口左转车均延误下降40%左右,而总车均延误下降率呈上升趋势,这是因为此时交通量较小,移位左转交叉口的周期保持不变,为最小信号周期(满足行人过街).因此随着饱和度的增加,其绿灯时长不变,左转车均延误增长与传统交叉口类似.而移位左转信号为两相位,传统交叉口信号为三相位,因此其直行车均延误增长低于传统交叉口.当交叉口饱和度大于0.8时,传统交叉口总车均延误与左转车均延误急剧增加,因此移位左转交叉口的总车均延误与左转车均延误下降率也随之增大.

3.1.2 双移位左转车道方案效用分析

不同直行交通量会对移位左转的效果产生不同的影响,因此需探究左转车流量与南北、东西直行车流量和移位左转车道数之间的关系.以南北方向设置移位左转车道为例：保持南北直行与东西直行交通量不变,当南北直行交通量大于、等于和小于东西直行交通量,即q2,4=1 400 pcu/h,q1,3=800 pcu/h；q2,4=1 200 pcu/h,q1,3=1 200 pcu/h；q2,4=800 pcu/h,q1,3=1 400 pcu/h时,将左转车流量调整为q5,6=300,400,…,1 000 pcu/h,得到在不同移位左转车道数情况下交叉口的总车均延误与左转车均延误,如图7～图9所示.

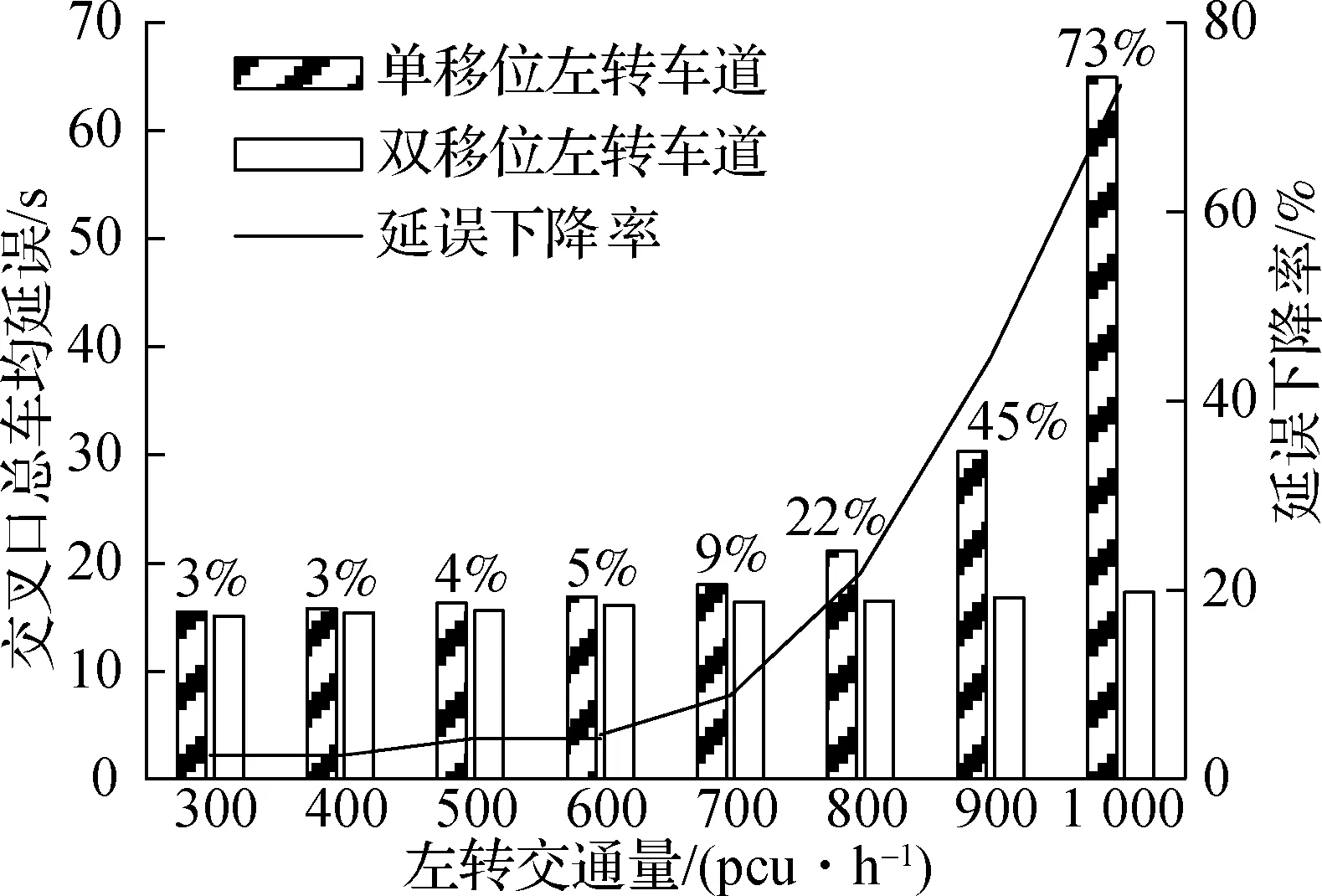
(a) 交叉口总车均延误

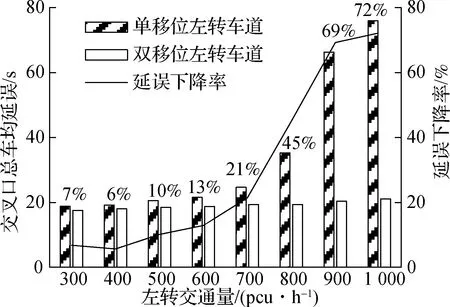
(a) 交叉口总车均延误

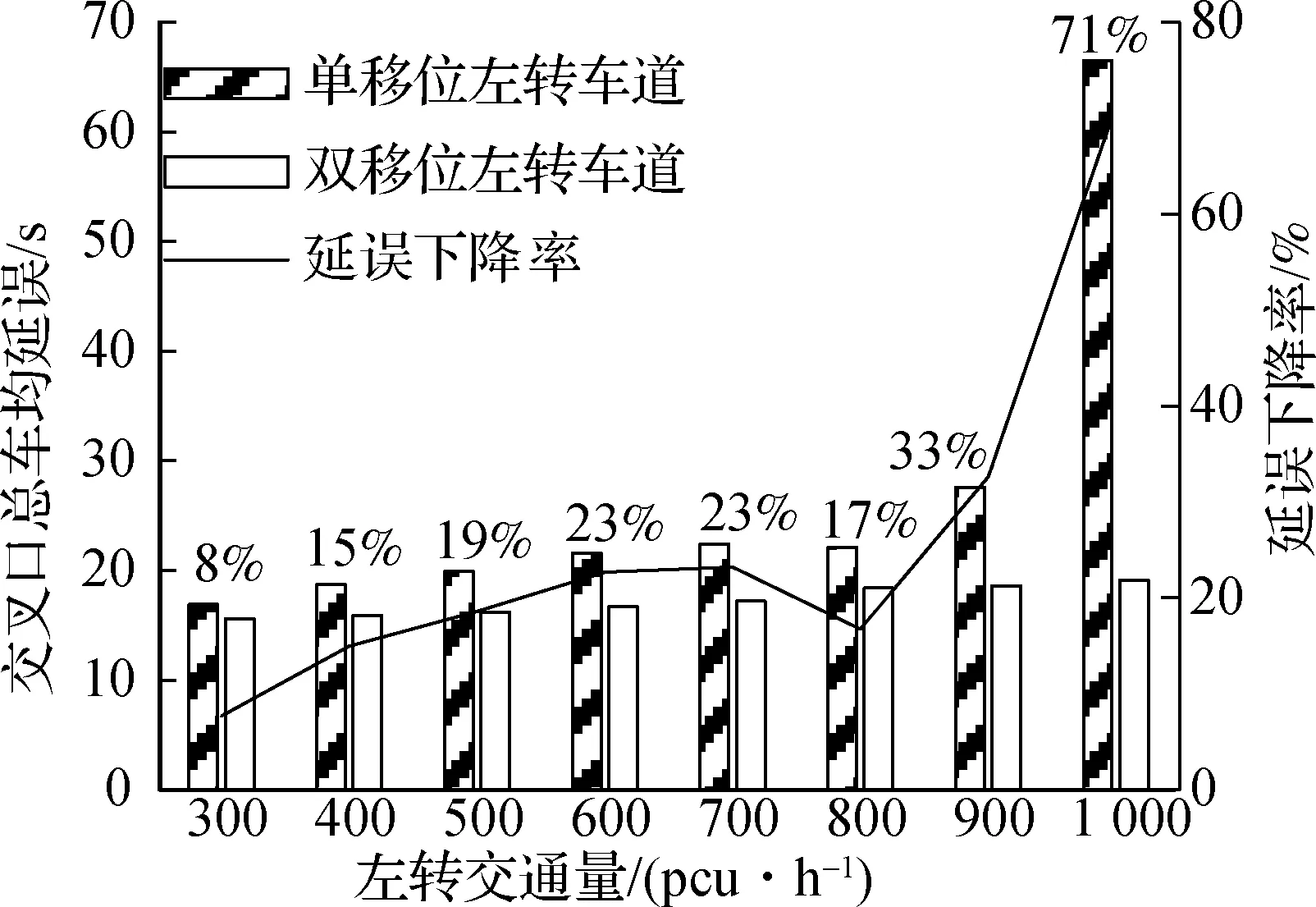
(a) 交叉口总车均延误

由图7可知，当左转交通量小于700 pcu/h时，双路段、双移位左转车道(简称双道)总车均延误的下降率较低，当左转交通量大于700 pcu/h时，双道的延误下降率急剧增加.这是因为南北单路段、单移位左转车道(简称单道)的车道数是其直行车道数的一半，且主交叉口南北左转与直行绿灯一致，当其左转交通量大于直行交通量一半时就会遇到瓶颈，其左转车均延误开始增加，当左转交通量大于最大通行能力时，左转车均延误开始急剧增加.而南北双道的车道数等于南北直行车道数，道路通行能力较大，因此其车均延误上升幅度较小，延误下降率急剧上升.

由图8可知，双道延误下降率随左转交通量的增加而增加，当左转交通量大于600 pcu/h时，双道的延误下降率急剧上升.这是因为南北与东西直行交通量相等且大于南北左转交通量，因此相位1与相位2的绿灯时长基本一致，双道的延误下降率上升幅度较小.由于单道的车道数是南北直行车道数的一半，当南北左转交通量大于南北直行交通量一半，即600 pcu/h时就会遇到瓶颈，因此单道的左转与总车均延误的上升幅度变大，双道的延误下降率变大.当左转交通量大于800 pcu/h时，单道的道路通行能力已低于左转交通量，其车均延误急剧上升，因此双道的延误下降率急剧增加.

由图9可知，双道较单道的延误下降率先上升后下降再上升，这是因为一开始南北直行加左转交通量小于东西直行交通量，相位1的绿灯时长小于相位2，延误下降率呈上升趋势.当南北左转交通量大于600 pcu/h，即南北直行加左转交通量大于东西直行交通量时，相位1的绿灯时长会大于相位2，同时左转交通量小于单道左转的最大通行能力，因此左转车均延误达到最小，双道的左转车均延误下降率降低，导致总交叉口的车均延误下降率也随之降低.当南北左转交通量大于800 pcu/h时，单道的左转交通量大于道路最大通行能力，因此延误急剧增加，双道的延误下降率也迅速上升.

因此，若主信号相位数为n，当左转交通量大于移位左转车道的通行能力z/n时(z为移位左转车道组的饱和流率)，建议增加1条路段左转车道和1条移位左转储存道.

3.2 基于绿波控制的移位左转方案案例分析

本文以武汉市中山路与民主路交叉口为例开展对比分析,利用VISSIM仿真软件验证优化方案的实际效果.交叉口几何条件与移位左转渠化方案如图10和图11所示,各进口道高峰小时交通量如表1所示.

表1 武汉市中山路与民主路交叉口交通流量调查表 pcu/h

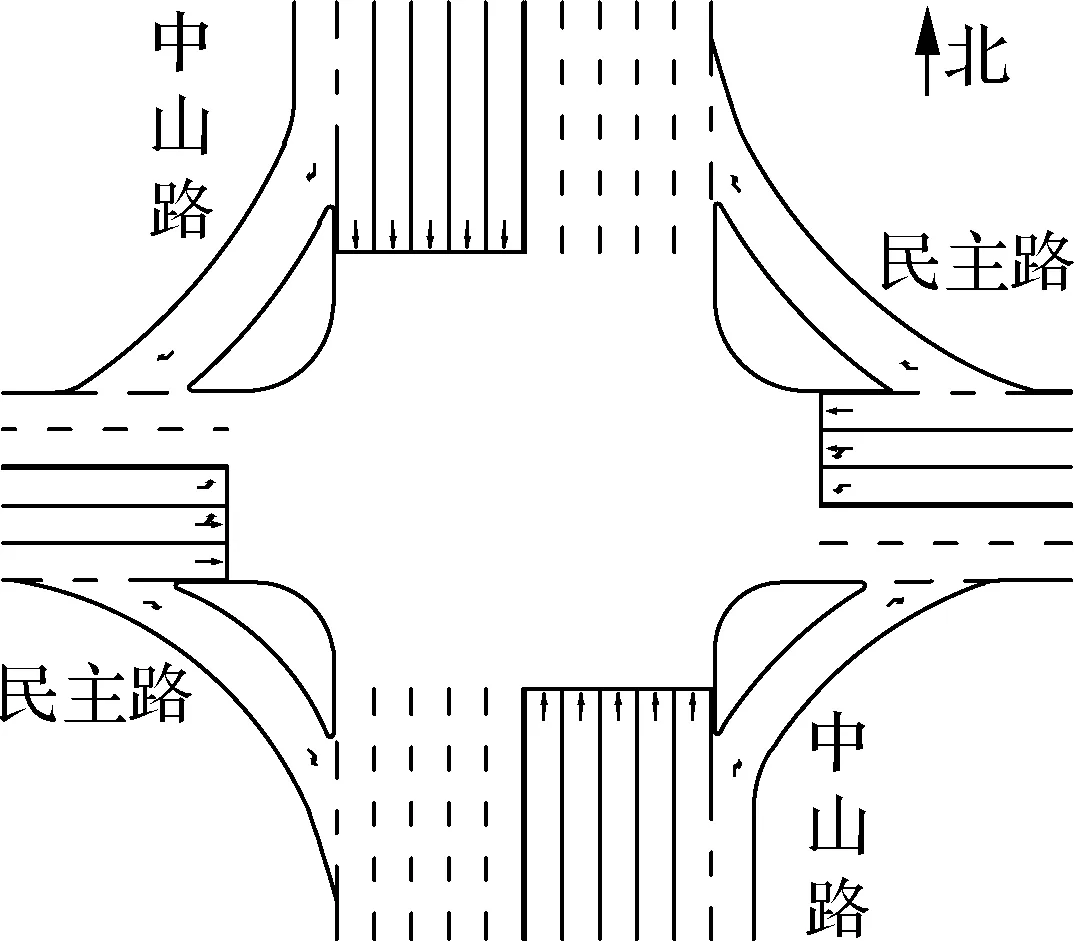
图10 交叉口现状渠化方案

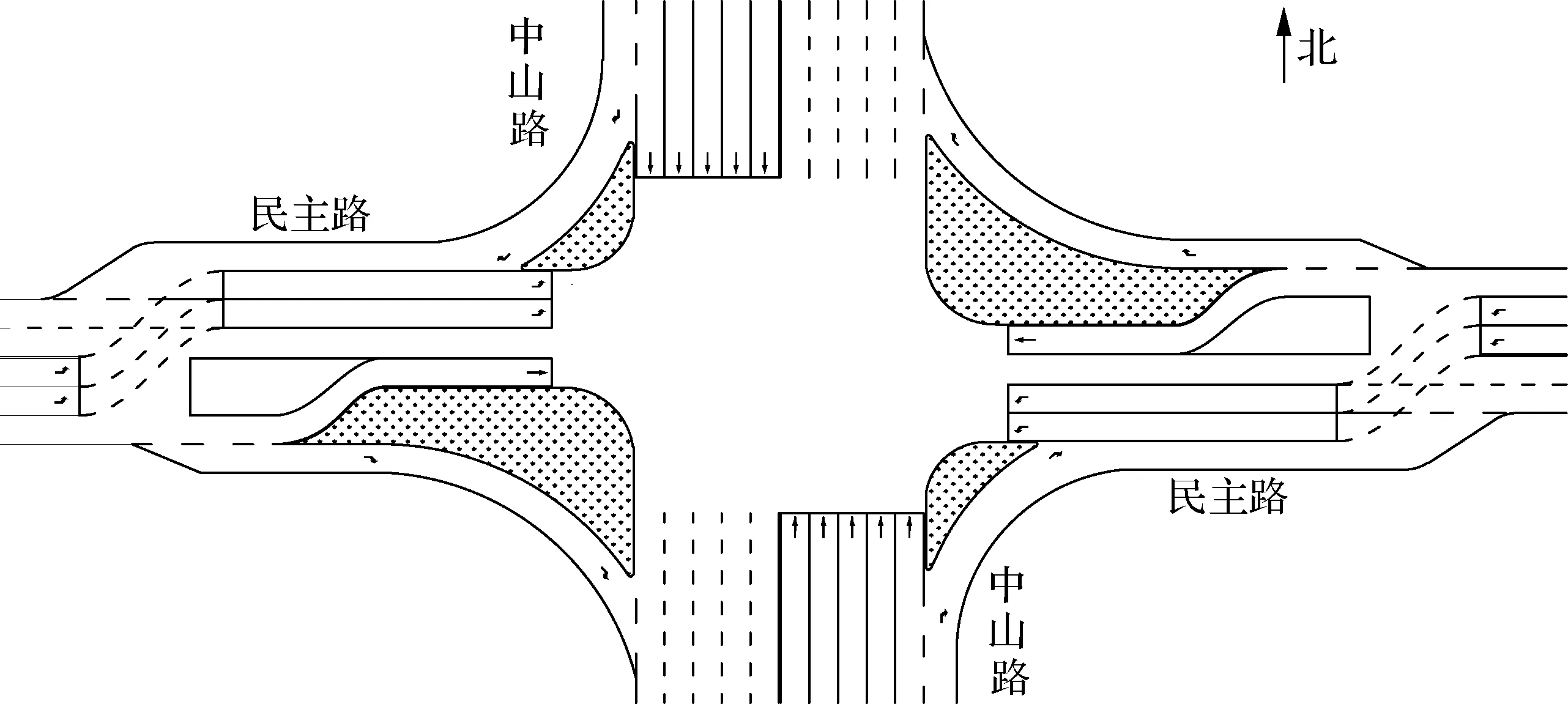
图11 交叉口移位左转渠化方案

针对上述渠化方案,分别构建交叉口现状信号控制方案(方案a),常规移位左转信号控制方案(方案b)和本文提出的基于绿波控制的移位左转信号优化控制方案(方案c),如图12所示.保持输入的高峰小时交通量和各类参数不变,以车均延误与停车次数为评价指标,得到3种信号控制方案下的仿真结果,如图13所示.

由图13可知，在高峰小时交通流量下，由于方案b未考虑协调控制，因此较方案a会显著增加左转车流的停车次数，影响驾驶舒适性.本文基于绿波控制理论将主、预信号进行协调控制，使左转车流驶出路段交叉口后可直接通过主交叉口.因此方案c较方案b在直行车均延误与停车次数上无改善效果，而在左转车均延误与停车次数上改善效果较好.同时，由于该交叉口东西左转交通量较小，因此方案c较方案b在交叉口总车均延误上改善效果不明显.

(a) 方案a

综上,方案c较方案a、方案b可以分别降低交叉口总车均延误57.8%、7.6%,停车次数26.7%、19.8%；降低东西进口左转车均延误55.0%、48.2%,停车次数11.1%、57.5%.这说明本文提出的方案可以极大程度上降低移位左转车辆的车均延误与停车次数,进一步改善移位左转交叉口.

4 结论

1) 基于移位左转交叉口的特性,提出了移位左转交叉渠化方案,针对出口道右转展宽段设计了计算模型,解决了交叉口右转车流与移位左转车流之间的冲突,降低了左转车的车均延误.

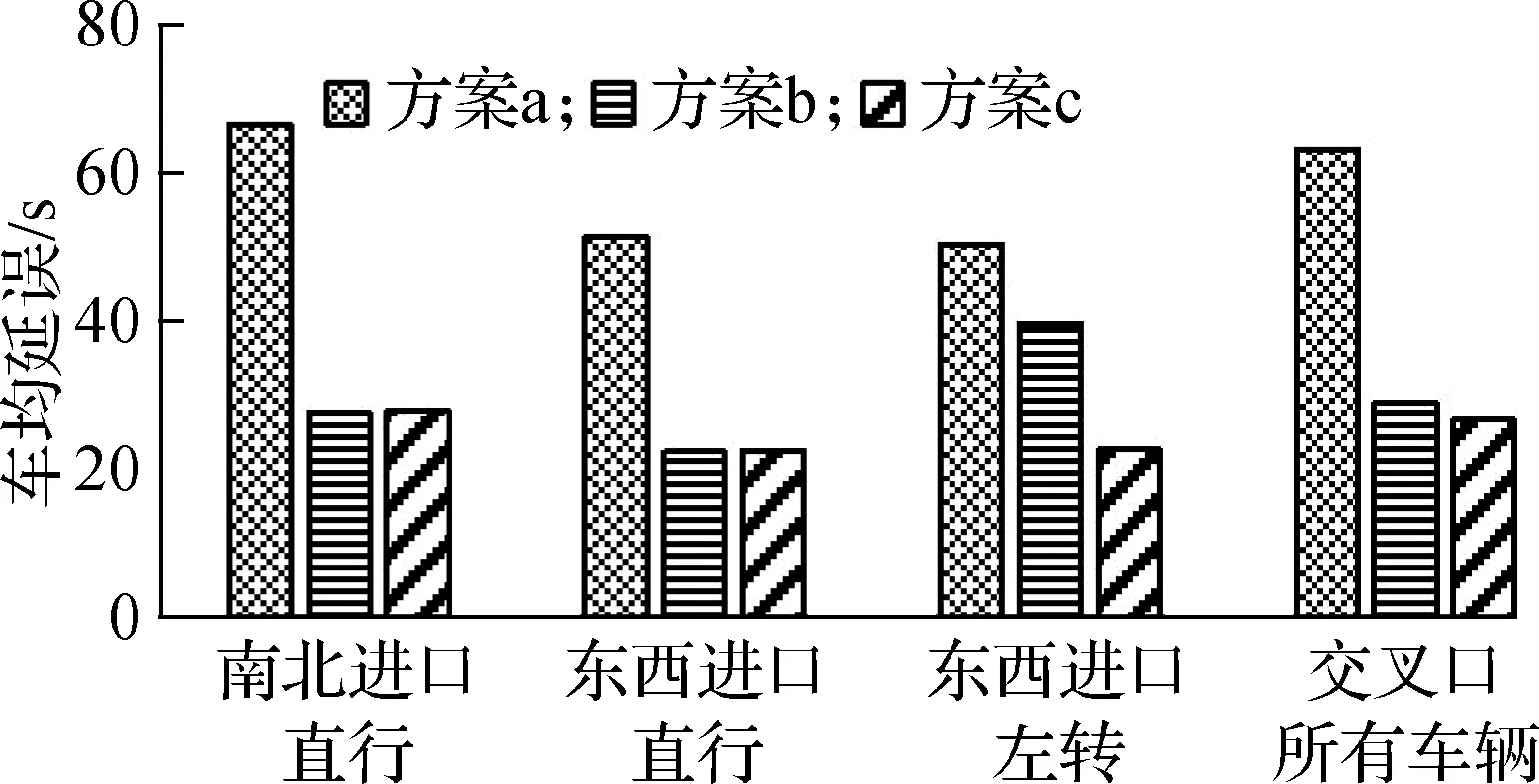
(a) 车均延误

2) 分析了预信号与主信号之间的复杂关系,建立了考虑绿波控制的移位左转车辆延误计算模型,并以直行与左转车流总车均延误最小为目标,构建了考虑绿波控制的双相位移位左转交叉口信号配时优化模型.

3) 分别从交叉口饱和度、左转交通量、直行交通量3个方面对基于绿波控制的移位左转交叉口信号控制方案的适用性进行了分析.当交叉口饱和度大于0.8时,改善效果明显；当左转交通量大于移位左转车道的通行能力时,建议增加1条路段左转车道和1条移位左转储存道.当左转交通量较大,其余交通量较小时,采用基于绿波控制的移位左转信号控制方案,交叉口的总车均延误降低效果更加显著.本文未考虑4个方向均有左转车流的情况,同时,大型车对于移位左转储存道长度设置效果的影响也有待进一步研究.