突出煤层区域预测指标W-P 模型优化及应用

衡献伟，李青松 ，3

（1.贵州省煤矿设计研究院有限公司，贵州 贵阳 550025；2.贵州省矿山安全科学研究院有限公司，贵州 贵阳 550025；3.中国矿业大学 安全学院，江苏 徐州 221116）

随着煤矿开采深度的增加，煤与瓦斯突出危险性也将随之加大，煤矿瓦斯防治措施也将由“局部性”向“区域性”转变，科学、准确测定区域预测指标是预测采掘工作面煤与瓦斯突出危险性的关键环节，现行《煤矿安全规程》、《防治煤与瓦斯突出细则》等规程规范将煤层瓦斯压力和瓦斯含量作为主要区域预测指标，并分别给出了推荐临界值。然而受现场测试条件等因素影响，为了快速获取煤层瓦斯含量及煤层瓦斯压力指标，常采用间接法即利用二者之间的关系进行相互反演计算[1-2]。研究表明：煤的可燃质吸附瓦斯含量与瓦斯压力服从朗格缪尔方程[3-5]，煤的游离瓦斯含量与瓦斯压力层呈线性关系，煤层保持完整或较完整状态时煤层瓦斯压力与瓦斯含量可以采用朗格缪尔方程互相反算；煤层处于破碎离散状态时，则煤层以块状呈现，瓦斯压力与瓦斯含量不适用朗格缪尔方程。以贵州煤矿区为例，直接套用经典模型进行反演计算，不同矿区、不同构造单元煤层瓦斯含量和瓦斯压力临界值差别较大，如响水煤矿5#煤层瓦斯压力0.74 MPa 反演瓦斯含量为11.28 m3/t，瓦斯含量8 m3/t 反演瓦斯压力仅0.52 MPa；林华煤矿9#煤层瓦斯压力0.74 MPa、瓦斯含量8 m3/t 条件下反演瓦斯含量和瓦斯压力分别为16.10 m3/t 和0.40 MPa。实践表明，根据W-P经典模型反演瓦斯含量或瓦斯压力数值与实测值存在一定误差[6-7]，其反演值误差具有随煤的破坏程度、瓦斯放散初速度的提高而增加的趋势。Langmuir经典物理模型建立的基本假设为：分子呈单分子层吸附状态，且固体表面均匀，被吸附在固体表面的分子无分子间相互作用力，吸附平衡为动态平衡[7]。诸多学者在多年研究过程中均有发现基于Langmuir方程的W-P 经典模型精度存在一定局限性，存在误差的原因既有测试误差的客观因素，也有模型精度存在局限性等因素[8-10]。为此，通过分析大量实测数据，引入煤的破坏系数X 和瓦斯放散初速度△p 这2 个参数，建立了W-P 优化模型并进行验证，为区域突出危险性预测和效果检验等获取可靠的瓦斯压力和瓦斯含量具有重要意义。

1 W-P 模型构建

1.1 数据基础

收集了贵州8 个矿区57 对矿井107 组数据，涉及盘江、水城、六枝、织纳、黔北、黔西北、林东、普兴等重点矿区及核心矿区的主要开采煤层，贵州省部分地区煤层瓦斯参数见表1（1 mmHg=133.322 4 Pa）。

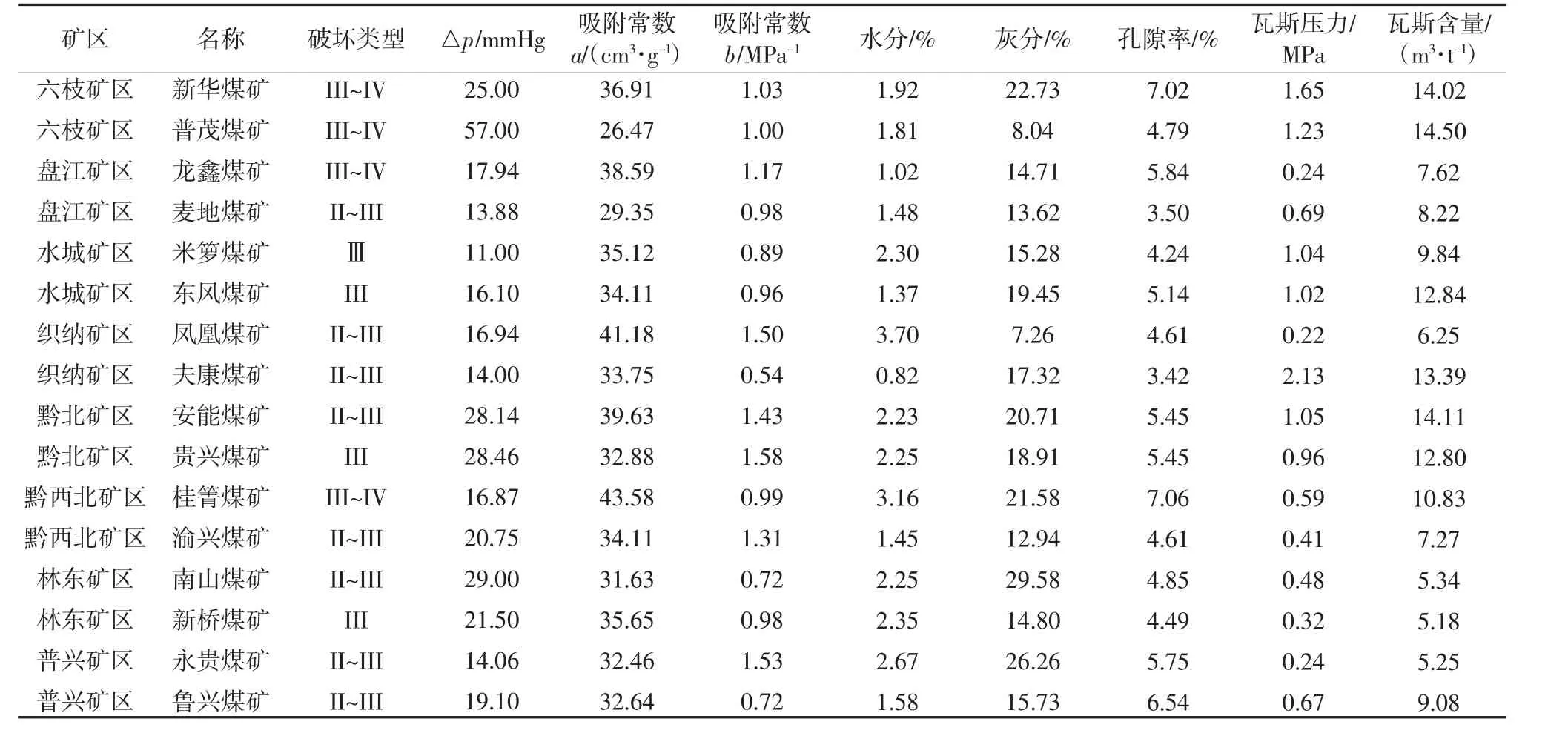
表1 贵州省部分地区煤层瓦斯参数Table 1 Characteristic parameters of coal samples

1.2 W-P 优化模型构建

W-P 经典模型如下：

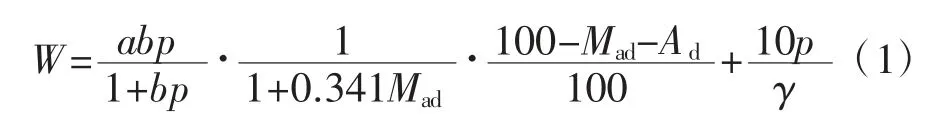
式中：W 为瓦斯含量，cm3/g；a、b 为吸附常数，无量纲；p 为瓦斯压力，MPa；Mad为水分，%；Ad为灰分，%；γ 为视密度，g/cm3；π 为孔隙率。

根据W-P 经典模型，将获得的实测瓦斯压力反演计算瓦斯含量并与实测瓦斯含量进行对比及根据获得的实测瓦斯含量反演计算瓦斯压力并与实测瓦斯压力进行对比可知，根据式W-P 经典模型反演获得的数据与实测数据存在明显误差，反演获得的瓦斯含量均要小于实测值，这是煤体孔隙内部填充的游离瓦斯计算量偏低引起的[11-13]，准确计算煤层中游离瓦斯含量是保证模型精度的关键；而反演获得的瓦斯压力均大于实测值，说明在贵州煤矿区直接套用W-P 经典模型反演所获得的参数存在较大误差。

李志强等[14-16]构建了动扩散系数新扩散模型，其模型对扩散过程的描述精度要高于W-P 经典扩散模型，动扩散系数新扩散模型的理论的基本假设为：煤体内部是由大量尺度不一的孔隙构成的，瓦斯从煤体内部扩散至外界时，首先从大孔中开始逸散，然后是中孔，其次是小孔、微孔。基于此分析认为，在测试瓦斯放散初速度△p 时（在1 个大气压下煤吸附瓦斯后用mmHg 表示45～60 s 与0～10 s 内的瓦斯放散量的差值），前1 min 瓦斯放散过程中，瓦斯主要来源是孔隙中的填充游离瓦斯，瓦斯放散初速度在一定程度上可以反映煤体孔隙中游离瓦斯特征，从时间尺度上来看，瓦斯放散初速度△p 测试值更多反映的是孔隙中填充游离瓦斯的放散能力。同时，多位学者对瓦斯压力、瓦斯含量、煤的孔隙结构、比表面积、瓦斯放散初速度等参数进行了研究，发现这些参数具有一定的内在关联性[17-21]。

根据统计数据，不同△p 区间平均实测瓦斯含量-压力变化如图1。由图1 可知，不同△p 区间平均实测瓦斯含量及压力均随着瓦斯放散初速度增大呈先减小后增大的趋势。

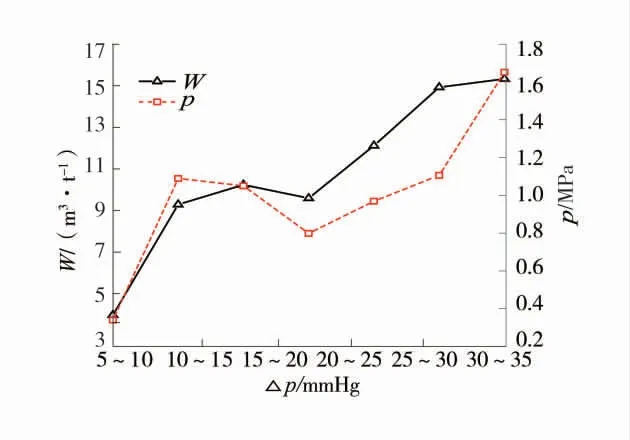
图1 不同△p 区间平均实测瓦斯含量-压力变化Fig.1 Variation of average gas content-pressure in different △p

不同破坏类型煤的平均实测瓦斯含量-压力变化如图2。由图2 可知，不同破坏类型煤的平均实测瓦斯含量及压力均随着煤的破坏程度的增大呈减小趋势。

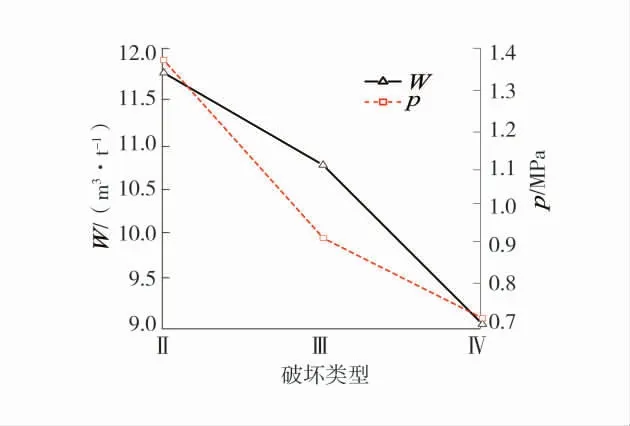
图2 不同破坏类型煤的平均实测瓦斯含量-压力变化Fig.2 Variation of average gas content-pressure in different failure types

基于诸多学者的研究成果可知，煤的破坏类型和放散初速度是煤物性的宏观表征，结合分析破坏类型和放散速度的影响，通过引入破坏类型和放散初速度这2 个指标，可以体现W-P 模型的多参数性和全局性。

通过对统计的贵州省煤矿地区107 组煤层瓦斯基础参数进行分析和拟合，根据煤的破坏类型引入了破坏系数X 概念，结合瓦斯放散初速度△p 可以反映孔隙中游离瓦斯放散能力特征，建立了W-P 优化模型：

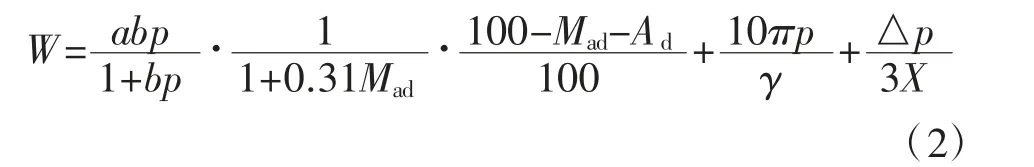
不同级别煤的破坏类型对应的破坏系数见表2。当测试区域煤的破坏类型介于2 种破坏类型之间时，取二者对应破坏系数的均值。

表2 破坏类型对应的破坏系数Table 2 Failure coefficients corresponding to failure types

2 W-P 优化模型与经典模型对比

2.1 瓦斯含量对比

基于实测瓦斯压力，将统计的107 组瓦斯参数数据分别代入W-P 经典模型及优化模型进行反演得到瓦斯含量。W-P 经典模型、W-P 优化模型反演瓦斯含量与实测瓦斯含量对比如图3、图4。

图3 W-P 经典模型反演瓦斯含量与实测瓦斯含量对比Fig.3 Comparison of gas content retrieved by W-P classical model and measured gas content

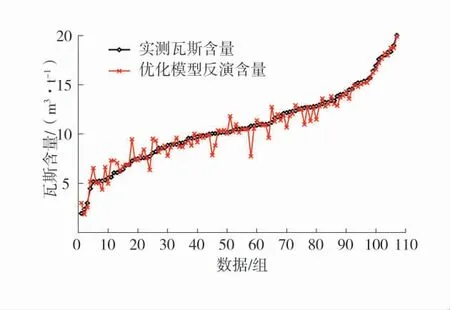
图4 W-P 优化模型反演瓦斯含量与实测瓦斯含量对比Fig.4 Comparison of gas content retrieved by W-P optimization model and measured gas content

由图3 和图4 可以看出，根据W-P 经典模型，实测瓦斯压力反演瓦斯含量整体上要小于实测瓦斯含量；W-P 优化模型反演的瓦斯含量与实测瓦斯含量拟合度较好，数据整体围绕实测瓦斯含量波动，且实测瓦斯含量越高，W-P 优化模型反演的瓦斯含量与实测含量拟合度越高，波动误差减小。

2.2 瓦斯压力对比

基于实测瓦斯含量，将统计的107 组瓦斯参数数据分别代入W-P 经典模型及优化模型进行反演得到瓦斯压力。W-P 经典模型、W-P 优化模型反演压力与实测瓦斯压力对比如图5、图6。

由图5 可以看出，W-P 经典模型反演得到的瓦斯压力整体上要大于实测瓦斯压力，并随着瓦斯压力的增大，反演压力在较大范围内波动，误差增大。由图6 可以看出，W-P 优化模型反演得到的瓦斯压力整体上围绕着实测瓦斯压力上下波动，并随着瓦斯压力的增大其拟合度逐渐提高。

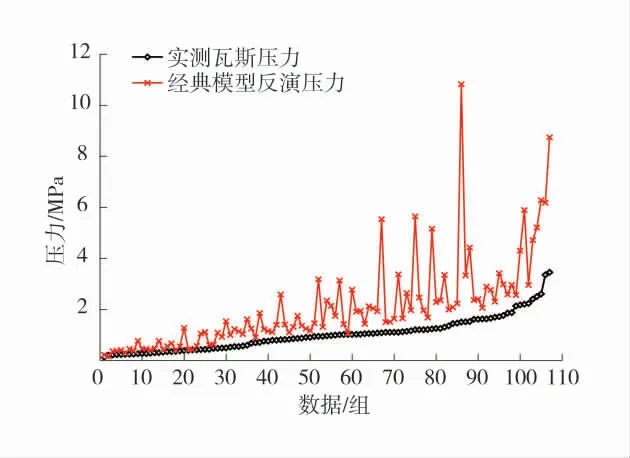
图5 W-P 经典模型反演瓦斯压力与实测瓦斯压力对比Fig.5 Comparison of gas pressure retrieved by W-P classical model and measured gas pressure

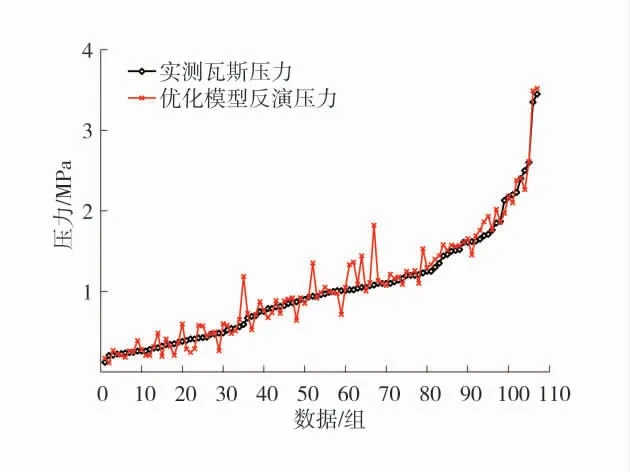
图6 W-P 优化模型反演瓦斯压力与实测瓦斯压力对比Fig.6 Comparison of gas pressure retrieved by W-P optimization model and measured gas pressure

3 基于W-P 优化模型的区域预测指标临界值确定

3.1 区域预测指标敏感性分析

矿井位于黔西县，设计生产能力为120 万t/a，矿井瓦斯等级为煤与瓦斯突出矿井。现主要开采M16、M18 2 个煤层，均为突出煤层，根据实测M16煤层的吸附常数（a=37.13 cm3/g，b=1.08 MPa-1）、工业分析（Mad=2.06%、Aad=15.12%、Vad=6.63%）和煤的坚固性系数（f=0.28）、瓦斯放散初速度（△p=32.65 mmHg）等瓦斯参数，应用W-P 优化模型绘制瓦斯压力与瓦斯含量关系，M16 煤层W-P 对应关系如图7。

由图7 可知，M16 煤层瓦斯含量8.0 m3/t 对应的瓦斯压力为0.39 MPa；瓦斯压力0.74 MPa 对应瓦斯含量为11.52 m3/t。相比《防治煤与瓦斯突出细则》中，瓦斯压力的突出临界值为0.74 MPa，瓦斯含量的临界值为8.0 m3/t，M16 煤层煤样具有典型的“低压力高含量”特征。分析认为，这可能与M16 煤层为高变质程度的无烟煤有关，煤样具有较高的吸附能力，在相同的游离瓦斯压力下被吸附在煤层中的瓦斯量更高，M16 煤层的瓦斯含量比瓦斯压力更敏感。

图7 M16 煤层W-P 对应关系Fig.7 W-P correspondence of M16 coal seam

3.2 区域预测指标临界值

M16 煤层瓦斯压力与瓦斯含量在临界值条件下的对应关系见表3。反演瓦斯含量与实测瓦斯含量对比如图8，反演瓦斯含量误差分析如图9。

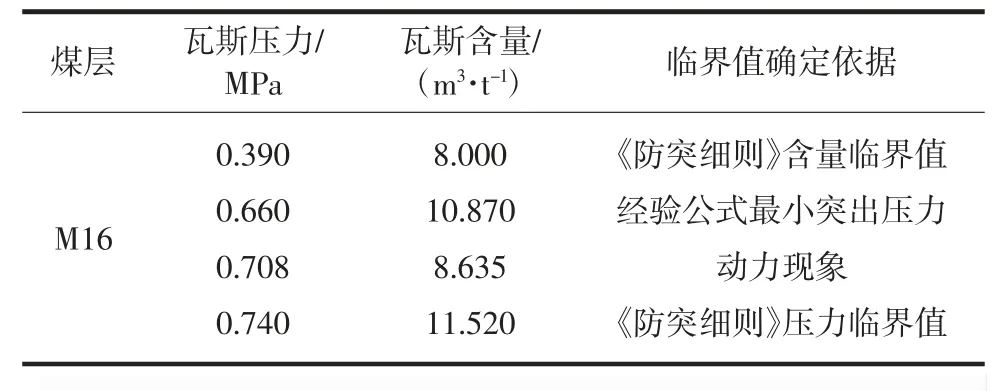
表3 瓦斯压力与瓦斯含量在临界值条件下的对应关系Table 3 Relationship of W-P under the condition of critical value

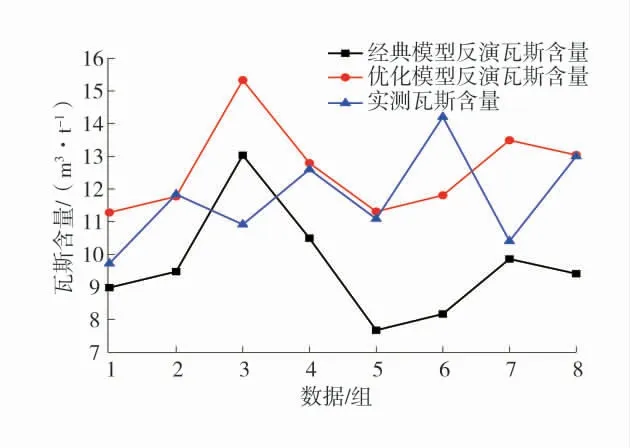
图8 反演瓦斯含量与实测瓦斯含量对比Fig.8 Comparison of inversion and measured gas content

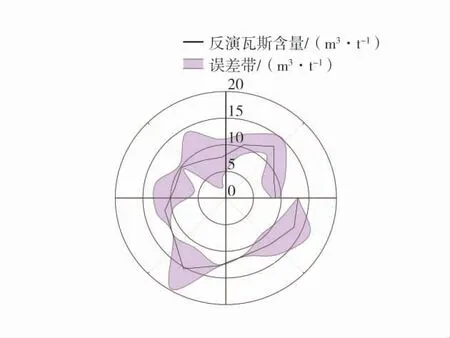
图9 反演瓦斯含量误差分析Fig.9 Error analysis of gas content inversion

由图8 可知，反演出得到的大部分瓦斯含量值高于《防突细则》中瓦斯含量8 m3/t，并且数据组反演出的瓦斯含量平均值为11.09 m3/t。由图9 可知，误差带是由瓦斯含量绝对误差的正负值构成，利用该误差带求得误差较小的瓦斯含量，利用求出的瓦斯含量计算平均值为9.03 m3/t。由于瓦斯含量临界值的国家标准为8.0 m3/t，和矿上的动力现象对应的瓦斯含量差距较小，考虑一定的安全系数（折算安全系数包含的因素为：人为技术带来的误差、地下随采掘等其他工程的扰动导致的应力重分布等导致原有实测数据的可靠性失准等误差）将M16 煤层瓦斯含量敏感指标临界值定为8.0 m3/t。

反演瓦斯压力与实测瓦斯压力对比如图10。由图10 可知，反演出得到的大部分瓦斯压力值高于《防突细则》中瓦斯压力0.74 MPa，并且数据组反演出的瓦斯压力平均值为1.30 MPa。

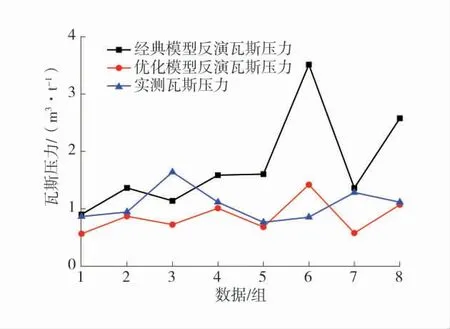
图10 反演瓦斯压力与实测瓦斯压力对比Fig.10 Comparison of inversion and measured gas pressure

反演瓦斯压力误差分析如图11。由图11 可知，误差带是由瓦斯压力绝对误差的正负值构成，利用该误差带求得误差较小的瓦斯压力，利用求出的瓦斯压力计算平均值为0.71 MPa。由于瓦斯压力临界值的国家标准为0.74 MPa，和矿上的动力现象对应的瓦斯压力差距较小，考虑到一定的安全系数将M16 煤层瓦斯压力敏感指标临界值定为0.70 MPa。

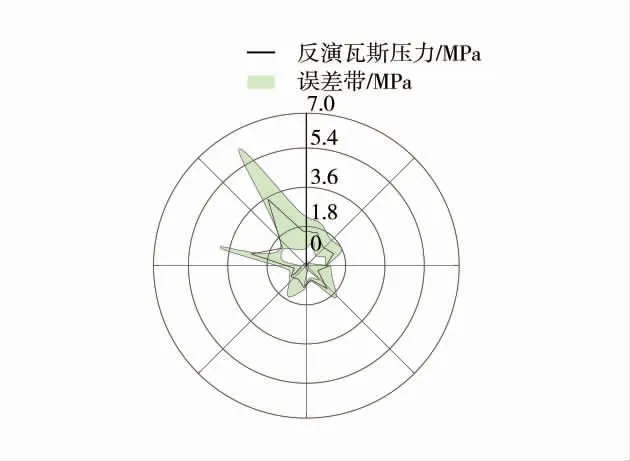
图11 反演瓦斯压力误差分析Fig.11 Error analysis of gas pressure inversion

4 结 语

1）通过对贵州不同矿区、不同含煤构造单元大量瓦斯基础参数分析和拟合，根据煤的破坏类型引入了破坏系数X，基于此建立了W-P 优化模型。

2）经典模型反演值误差随着瓦斯放散初速度的增大呈显著递增趋势，优化模型显著控制了反演值误差随放散初速度增大其误差扩大的趋势。

3）对W-P 优化模型进行考察，W-P 优化模型获得的反演瓦斯含量及反演瓦斯压力平均相对误差分别为6.44%和14.27%，相对W-P 经典模型，W-P优化模型的平均相对误差分别降低了17.54%和83.59%，表明W-P 优化模型可靠性较高。

4）基于W-P 优化模型确定量矿井M16 煤层区域预测指标瓦斯含量和瓦斯压力临界值分别为8.0 m3/t 和0.74 MPa，与M16 煤层实际发生瓦斯动力现象处的瓦斯含量和瓦斯压力值相吻合。