基于PSO算法优化BP神经网络的金融风险防范预警模型研究
吴川惠 王昭
(西安欧亚学院,陕西 西安 710065)
传统的BP神经网络模型丰富了金融风险预警模型体系,能够实现从输入到输出过程复杂非线性的映射,具有很强的学习能力,但BP神经网络算法易陷入局部最优解,而随机的初始化权值和阈值使其出现每次训练的结果都不一致的情况。本文将利用种群中个体对信息共享的特征,可以自适应地调整搜索方向,以便具备隐行性和全局寻优能力的粒子群优化算法(PSO)对BP神经网络的权值和阈值进行优化,以此解决BP神经网络存在的局部收敛性问题,从而动态地在海量数据中提取隐藏规律,提高对经济指标的全局搜索和预测能力。
一、金融风险防范预警指标体系
金融风险预警模型防范金融风险,需要通过实时地监测金融指标的动态变化来实现,所以指标体系的构建需要具有时效性、灵敏性、可操作性以及系统性等特点。通过借鉴国内外相关文献和访谈相关专家,确定了三大类风险为金融监管风险、金融机构风险以及证券保险国际收支的交叉类风险。本文以科学性和有效性原则,构建了与金融风险预测相适应的预警指标体系,涉及9类具体风险类型和24个变量指标。根据上述各大类风险中具体风险的变量指标,选取2010—2019年我国相关金融数据作为样本(见表1),用以检验预警模型的金融风险预测效果。

表1 金融风险防范预警指标体系
二、金融风险防范预警模型构建
针对BP神经网络具有收敛速度慢、易陷入局部极值点、学习过程易发生振荡和训练时学习新样本过程中有遗漏旧样本等问题。本文将PSO算法对BP神经网络的权值和阈值进行优化,以解决这些问题。基于PSO优化的BP神经网络主要流程如下:
Step1:设定神经网络的输入层节点数、隐层节点数和输出层节点数以确定BP神经网络拓扑结构,确定神经网络的权值和阈值的函数分量,以方便后续调用优化。
Step2:初始化粒子群的速度、最大迭代次数、学习因子、种群规模和粒子位置。
Step3:通过网络训练,计算粒子的适应度函数值,得到粒子个体最优解和全局最优解,通过比较,记录粒子种群的最优位置。
Step4:重新调整当前粒子的速度和位置,将新个体插入到种群中,当训练网络的误差满足设定条件时,则终止迭代,计算并得到结果,否则转步骤3,继续迭代直至算法收敛。
Step5:将PSO优化的权值和阈值赋予BP神经网络的初始权值和阈值,获取优化后的BP神经网络结构,从而反复迭代完成训练,输出预测值。
三、金融风险防范预警模型实证检验
为了验证构建的金融风险防范预警模型可行性,本文采用Matlab2016a软件对金融风险防范预警模型进行训练和检验。
(一)粒子群算法预置参数
根据经验值进行设置,种群大小个数为300,最大速率0.01,适应度阈值0.000001,学习因子c1 = 2、c2 = 0.8,迭代次数n为500,粒子位置Xmax=1,Xm i n=-1,粒子的速度Vmax=1,Vm i n=-1,粒子的惯性权重w 采用线性递减方式其中Wmax=0.9,Wmin=0.3。
(二)BP神经网络预置参数
整个网络由3层构成,输入层节点数为9,主要输入2010年至2018年的24个指标的数据,输出层值为2019年度的预警指标数据,隐层节点数根据经验不断地进行网络训练,确定隐含层节点数为9时,误差较小且效果最优。传递函数Sigmoid,训练次数为1000次,训练目标是0.000001。
(三)模型评价指标
为了便于更加准确地评估金融风险防范预测模型的准确性,本文选用了2个评价指标,分别为平均绝对误差(MAE)和平均绝对百分误差(MAPE)。
(四)适应度曲线
在迭代进化过程中,前期减幅较大,而后平均适应度曲线总体下降趋势减缓,当迭代次数达到500时,适应度曲线逐渐趋于平缓(见图1)。

图1 适应度曲线
(五)优化的神经网络权值及阈值
迭代完成后,找到最优粒子,得到PSO优化的权值和阈值(见表2),将其最优粒子的位置向量值赋给BP神经网络的权值和阈值,使得BP神经网络性能达到最优。

表2 PSO算法优化BP神经网络的最优权值和阈值

?
(六)预测结果分析
由图2预测真实值可以看出PSO-BP神经网络模型的预测值与实测值非常接近,其中最大相对误差为1.5%,最大绝对误差为3.6,误差在可接受范围内,表明此算法性能较好,因此可以将预测结果用于模拟计算。
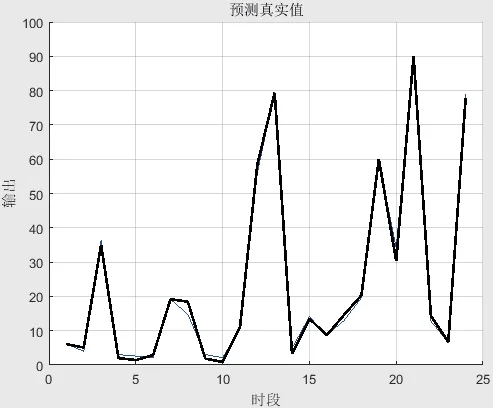
图2 预测真实值
四、结束语
运用PSO算法优化的BP神经网络模型进行数据处理,在对我国金融风险动态预测中,模型会自动吸取历年各个指标的历史变化趋势,挖掘出潜在可能存在的风险信息,比较准确的预测出期望年度各指标的数据,然后再与国家监管部门的风险阈值自动对比,形成风险地图,使得政府部门的干预措施具有战略性。构建金融风险防范预警模型,并以此为基础构建我国的金融风险监管体系,通过以上实证数据的检验具有可行性,推进了我国实施整个金融风险防范预警体系的信心。

