状态依赖脉冲Caputo分数阶微分方程解的存在唯一性*
李晓月, 王 奇
(安徽大学 数学科学学院,安徽 合肥 230601)
0 引 言
由于系统的脉冲时刻与系统状态有关,因此具状态依赖脉冲微分方程成为微分方程领域的难点问题,已有结果主要研究方程解的存在唯一性及稳定性,详见文献[1-7]。受已有文献的启发,利用不动点方法研究状态依赖脉冲Caputo分数阶微分方程
(1)
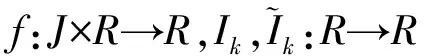
1 预备知识
记C(J,R)表示从J到R的连续函数组成的空间,其范数为
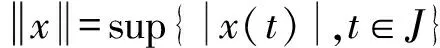
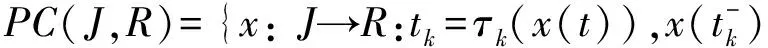
其中xk=xk(t),t∈(tk,tk+1]。
定义2.1[8-9]对任意函数h∈L1([a,b],R+),定义其分数阶积分
定义2.2[8-9]函数h在区间[a,b]上有定义,定义其Riemann-liouville分数阶导数为
其中n=[α]+1,[α]为取整函数。
定义2.3[8-9]对任意函数h在区间[a,b]上有定义,定义其Caputo分数阶积分为
其中n=[α]+1,[α]为取整函数。
引理2.1[10]若β>0,a(t)是区间[0,T),T≤+∞上的非负局部可积函数,b(t)是区间[0,T),T≤+∞上的非负、非减有界连续函数,y(t)是区间[0,T),T≤+∞上的非负局部可积函数。若
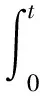
则

2 主要结论
(H1)f:J×R→R连续,存在函数M∈LP(J,R+),N使得


(H2)τk∈C1(R,R),k=1,2,…,m,并且
0<τ1(x)<…<τm(x) τk(Ik(x))≤τk(x)<τk+1(Ik(x)),x∈R。 定理2.1 若条件(H1)和的第二式及(H2)、(H4)及均满足,则方程式(1)至少存在一解。 证明首先考虑以下问题: (2) 定义F:C(J,R)→C(J,R)的算子为 (3) ① 在C(J,R)中取函数列xn→x,则由(H1)易得Fxn→Fx,n→∞,即算子F是全连续算子。 ② 取C(J,R)中有界集 由条件(H1)及赫尔德不等式得 (4) (5) 即算子F把有界集映成等度连续的。由Arezela-Ascoli定理知算子F是全连续的。 ④ 考虑集合 K={x∈C(J,R):x=λFx,0<λ<1} 的有界性。 对任意x∈K,则由条件(H1),类似于以上推导,有 (6) |x(t)|≤a(t)Eβ(b(T)Γ(β)tβ)≤H (7) 即集合K有界。 由Schaefer不动点定理得算子F存在不动点,即方程式(2)的解,记解为x1(t)。 考虑函数 rk,1(t)=τk(x1(t))-t,t≥0,k=1,2,…,m (8) 由条件(H2)得rk,1(0)≠0。若rk,1(t)≠0,t∈J,则x1(t)是方程式(1)的解。 下面考虑存在t∈J使得r1,1(t)≠0,由r1,1(0)≠0及r1,1(t)的连续性,存在t1∈J使得r1,1(t1)=0及r1,1(t)≠0,t∈[0,t1)。由条件(H2)得rk,1(t)≠0,t∈[0,t1),k=1,2,…,m。 考虑以下问题 (9) 在C([t1,T],R)定义算子F1为 (10) 类似于步骤一可得,算子F1是全连续的,有不动点x2。考虑函数 rk,2(t)=τk(x2(t))-t,t≥t1,k=1,2,…,m (11) 若rk,2(t)≠0,t∈(t1,T],则 (12) 是式(1)的解。考虑在t∈(t1,T]使得 r2,2(t)=0 (13) 由条件(H3)得 (14) 由r2,2(t)的连续性,存在t2>t1使得r2,2(t2)=0及r2,2(t)≠0,t∈(t1,t2)。由条件(H2)得 rk,2(t)≠0,t∈(t1,t2),k=2,…,m (15) (16) 与条件(H4)产生矛盾。 步骤三、类似于步骤一、二,利用数学归纳法,可以得到 (17) 的解xm(t),t∈(tm,T],从而得到方程式(1)的分段连续解 (18) 由条件(H2)的第二式及(H3)的第二式,利用压缩映射原理得: 定理2.2 若条件(H1)和的第一式及(H2)、(H4)均满足,并且 则方程式(1)存在唯一解。 和文献[1]比较,条件(H1)比文献[1]的条件(H2)更加宽松,已改进文献[1]的相关结果。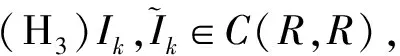

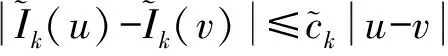
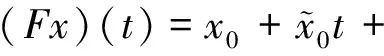
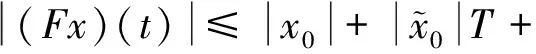
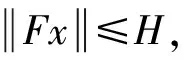

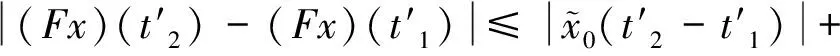


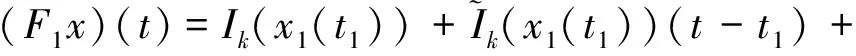

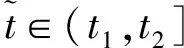
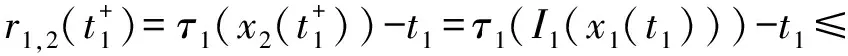
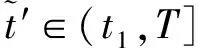

4 结束语

