截卵形头部平台直径对初始侵彻弹道偏转的影响

张丁山，谷鸿平，徐 笑，张 博，吕永柱

（西安近代化学研究所，陕西 西安 710065）

侵彻弹道偏转是考核战斗部侵彻性能的主要参数之一，尤其斜侵彻多层钢筋混凝土靶时，侵彻弹道偏转控制尤为重要。侵彻过程可分为弹头侵彻和弹体侵彻两个阶段：弹头率先侵彻，因弹头上下表面受力不均匀而产生偏转力矩，导致战斗部发生初始偏转；弹体侵彻时，受力不均匀产生的偏转力矩使战斗部在初始偏转的基础上进一步偏转，偏转程度可能减小也可能增强，直至战斗部完成侵彻。偏转力矩的大小与弹头形状、弹体外型直接相关，因此研究战斗部侵彻弹道的偏转性能时，分析弹头形状和弹体外型的影响至关重要。

截卵形是一种典型的侵彻战斗部头部形状。关于截卵形头部弹体的侵彻性能，我国已开展了大量的研究工作，如异形头部弹体的侵彻机理[1]、不同头部形状弹体侵彻混凝土性能[2]、斜侵彻弹道偏转[3]、截卵形弹丸侵彻混凝土性能[4]、截卵形弹体正侵彻加强筋结构靶[5]、非对称作用下的动态响应[6]、截卵形弹入水性能[7]、考虑弹头形状[8]和头部变形[9]的混凝土靶侵彻深度等。同时，研究人员还开展了相关侵彻仿真计算[10]，分析了尖卵形和截卵形头部结构对侵彻深度、侵彻弹道偏转的影响规律，建立了特定条件下侵彻特定靶标时弹靶相互作用的理论模型和仿真模型，得出了相对于尖卵形头部，截卵形头部的侵彻弹道稳定性较好而侵彻深度相对降低的定性结论，为战斗部设计提供了参考，但是对于战斗部结构优化设计，尤其在重点考虑弹道偏转控制和不同侵彻条件时，如何设计截卵形头部平台尚未开展深入研究。基于此，本研究拟通过理论分析和数值仿真计算，重点探讨截卵形头部不同平台直径对初始弹道偏转的影响，为该类型战斗部头部结构优化设计提供参考。

1 理论模型

以截卵平台中心O为原点，沿弹轴方向和垂直弹轴方向建立Oxy坐标系。如图1 所示，设弹轴与靶面法线的夹角为 φ；弹体圆弧段称为头部，弹体头部弧线延长线与弹轴的夹角为θ；截卵平台直径为d。侵彻着靶时率先接触靶面的头部侧面称为下表面，通过弹轴与之对称的头部侧面称为上表面。

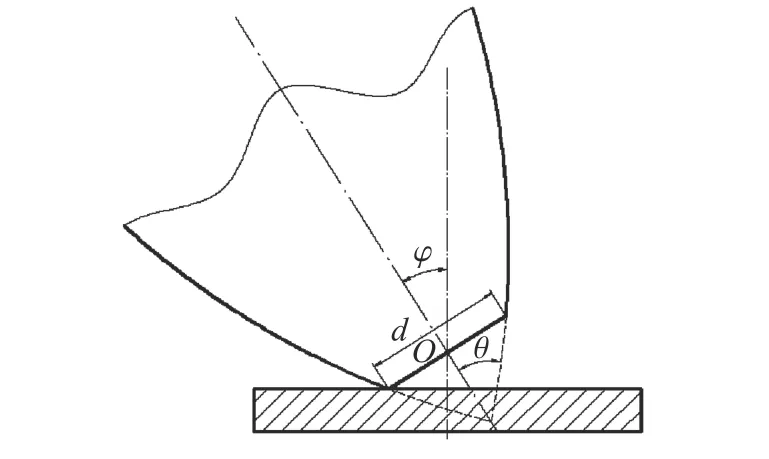
图1 侵彻靶标示意图Fig. 1 Schematic of the warhead penetrating a target

为使问题得到简化，作如下假设：

(1) 弹体为刚体，头部侵彻靶标时不发生变形；

(2) 不同截卵平台直径下，侵彻条件相同；

(3) 相同的侵彻条件下，侵彻过程中压垮单位面积混凝土产生的阻力相同；

(4) 侵彻速度方向与弹轴的方向相同，即攻角为0°；

(5) 理论计算中，进行对比的两个截卵平台直径变化幅度较小，即计算步长较小，以减小因不均衡力的力臂按照平均力臂计算所带来的误差。

侵彻时，存在弹轴与靶面法线的夹角 φ，弹体头部上下表面受到的阻力不同，导致沿平行弹轴方向和垂直弹轴方向产生不均衡力，该不均衡力以弹体质心为支点，产生偏转力矩；另外截卵平台的存在也会产生偏转力矩，进而引起弹体偏转。本研究只探讨截卵形头部侵彻产生的偏转，暂不分析弹体侵彻产生的偏转问题。

1.1 截卵平台直径对初始偏转的影响

根据基本假设，弹体头部侵彻时，分为截卵平台侵彻和弧面段侵彻。截卵平台侵彻时产生的平行弹轴的力Fpp为

截卵平台侵彻时产生的平行弹轴的力臂按di/4 （i=1, 2）计算，在截卵平台直径d1、d2之间的弧段侵彻时产生的平行弹轴方向不均衡力的平均力臂按 (d1+d2)/4计算，垂直弹轴方向的不均衡力的平均力臂按L计算，其中L为弹体质心距截卵平台中心的距离。设减小弹轴与靶标法线夹角的力矩方向为正方向，增大弹轴与靶标法线夹角的力矩方向为负方向。

垂直弹轴方向产生的偏转力矩差ΔMv为

表1 计算工况Table 1 Conditions of calculation

从图2 中可以得出：随着截卵平台直径的增大，侵彻时平行弹轴方向产生的偏转力矩为正，且逐渐增大；随着 φ 的增大，平行弹轴方向产生的偏转力矩增大；随着 θ 的增大，即头部形状系数（CRH）减小，在相同的侵彻条件下，平行弹轴方向产生的偏转力矩为正，且随着截卵平台直径的增大而增大，但增大幅度呈现减小趋势。

图2 不同工况下的f1(d1, d2)曲线Fig. 2 Curves of f1(d1, d2) under different conditions

从图3 中可以得出：随着截卵平台直径的增大，侵彻时垂直弹轴方向产生的偏转力矩为正，且逐渐增大；随着 φ 的增大，垂直弹轴方向产生的偏转力矩增大；随着 θ 的增大，即头部形状系数减小，在相同的侵彻条件下，垂直弹轴方向产生的偏转力矩为正，且随着截卵平台直径的增大而增大，但增大幅度呈现减小趋势。

图3 不同工况下的f2(d1, d2)曲线Fig. 3 Curves of f2(d1, d2) under different conditions

综上所述，随着截卵平台直径的增大，侵彻时产生的平行和垂直弹轴方向的偏转力矩均为正，且均逐渐增大，即产生的偏转力矩均使弹轴与靶标法线夹角减小，且随着截卵平台直径的增大，减小弹轴与靶标法线夹角的幅度增大，偏转角速度增大；随着头部角度 θ 的增大，即头部变钝，在相同的侵彻条件下，产生的偏转力矩减小，致使减小弹轴与靶标法线夹角的幅度减小，偏转角速度减小。

2 仿真模型

2.1 模型建立

应用ANSYS/LS-DYNA 程序建立仿真模型。对于壳体，采用与应变率相关的塑性随动硬化模型描述，并考虑失效；对于混凝土材料，采用JHC 累计损伤本构模型描述，钢筋采用beam 梁单元描述，钢筋与混凝土之间设置耦合关系；弹体与靶板之间采用面面侵蚀接触算法。本计算采用cm-g-μs 单位制，每20 μs 输出一次结果文件。弹体和靶标网格均采用拉格朗日网格算法，利用TRUEGRID 前处理软件完成有限元模型建立。考虑到模型结构具有对称性，建立1/2 计算模型，计算到弹体头部完全侵入靶标为止。

侵彻模型中，壳体材料选用G50 高强度钢，壳体材料参数见表2[11]，其中： ρ为密度，E为弹性模量，μ为泊松比， σ为动态屈服应力，Et为塑性剪切模量， β 为各向同性硬化系数，fs为失效应变系数。混凝土的JHC 本构模型参数和材料参数见表3[11]，其中：G为剪切模量，A为归一化黏聚强度系数，B为归一化压力硬化系数，C为应变率影响系数，N为压力硬化指数，fc为靶标抗压强度，T为抗拉强度， ε˙0为参考应变率， σfmin为 最小断裂应变，Sfmax为归一化最大强度，pc为压碎压力， μc为压碎体积应变，pL为压实压力，μL为压实体积应变，D1、D2为损伤常数，K1、K2、K3为混凝土材料常数。

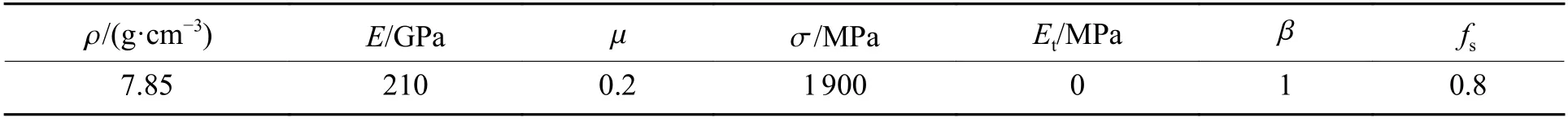
表2 壳体材料特性参数[11]Table 2 Material parameters of warhead shell[11]

表3 混凝土JHC 本构模型材料特性参数[11]Table 3 Material parameters ofJHC constitutive model of concrete[11]

2.2 模型校核

结合某240 kg 弹体（截卵形头部）以842 m/s 的速度、0°攻角、15°着角侵彻5 层C40 钢筋混凝土靶（厚度分别为300、180、180、180 、180 mm，每层间隔2.7 m）试验结果，对模型进行校核。该试验中，出靶后5 m 处的余速为570 m/s，弹体向下偏转22.6°，试验结果如图4 所示。弹体的结构参数：弹长1 150 mm；弹径280 mm；头部形状系数3.0；截卵平台直径40 mm；质心距头部顶点距离640 mm；x、y、z轴的转动惯量Ix= 2.68 kg·m2，Iy= 43.90 kg·m2，Iz= 43.90 kg·m2。

图4 侵彻试验结果Fig. 4 Result of penetration test

应用建立的数值仿真模型参数，对侵彻试验进行了仿真计算，着重计算侵彻前后弹体的偏转和速度变化情况，并与试验结果进行对比。仿真计算结果如图5 和图6 所示。

图5 弹道偏转仿真计算Fig. 5 Simulation result of ballistic deflection after penetration

图6 侵彻速度曲线Fig. 6 Curve of velocity during penetration

仿真计算结果显示，战斗部以850 m/s 的速度、15°着角侵彻5 层钢筋混凝土靶时，出靶后余速为568 m/s，弹体向下偏转24°。仿真计算结果与试验结果基本一致，表明仿真模型及参数准确。

2.3 计算结果

应用校核过的模型及参数，对3 个算例进行仿真计算，着重研究不同截卵平台直径的弹体头部侵彻靶标时产生的偏转情况。计算从截卵平台撞击靶标瞬间开始，到弹体头部完全侵入靶标为止。仿真计算模型如图7 所示。计算所用的弹体结构参数见表4，其中：Lp为弹体长度，dp为弹体外径，mp为弹体质量，d为截卵直径，S为质心与战斗部头部顶端面的距离。不同截卵平台直径的弹体头部侵彻靶标时产生的偏转角速度和偏转角度仿真计算结果如图8 和图9 所示。

表4 仿真算例参数Table 4 Parameters of simulation examples

图7 仿真计算模型Fig. 7 Numerical simulation model

通过图8 和图9 可以得出：在相同的侵彻条件下，随着截卵平台直径的增加，偏转角速度随之增大；在相同的截卵平台直径和相同的侵彻条件下，随着头部形状系数的减小，即头部变钝，偏转角速度随之增大。

从图2 和图3 中的工况2 可得，当k= 1.5 时（d1= 40 mm，d2= 60 mm），f1= 0.05，f2= 0.06，综合偏转力矩峰值（平行弹轴方向产生的偏转力矩和垂直弹轴方向产生的偏转力矩矢量和）约为40 mm 截卵平台直径时的1.5 倍；当k= 2.0 时（d1= 40 mm，d2= 80 mm），f1= 0.494，f2= 0.362，综合偏转力矩峰值约为40 mm 截卵平台直径时的2 倍。由图8 可得：截卵平台直径为60 mm 时的综合偏转力矩峰值约为平台直径40 mm 时的1.2 倍，截卵平台直径为80 mm 时的综合偏转力矩峰值约为平台直径40 mm 时的2 倍。

图8 不同截卵平台直径下的偏转角速度曲线Fig. 8 Curves of deflection angular velocity with different truncated ovate nose diameter

从图2 和图3 中的工况2 和工况6 可得，对于d1= 40 mm：当k= 1.1 时，工况2 与工况6 的f1比值约为1.0，f2的比值约为1.1，工况2 的综合偏转力矩约为工况6 的综合偏转力矩的1.5 倍；当k= 1.5 时，工况2 与工况6 的f1比值约为1.0，f2的比值约为1.2，工况2 的综合偏转力矩约为工况6 的综合偏转力矩的1.5 倍。由图9 可得， θ分别为25°和35°时，综合偏转力矩峰值的比值约为1.4。

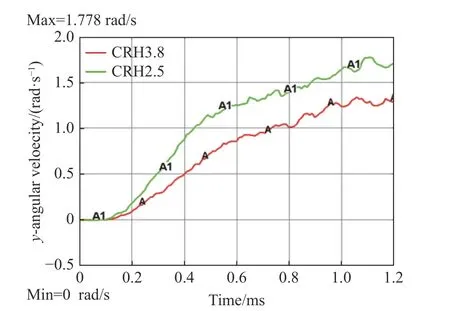
图9 不同头部形状系数下的偏转角速度曲线Fig. 9 Curves of deflection angular velocity with different head shape coefficient

对比理论计算和数值仿真结果得出，两种计算结果得到的趋势相同，理论计算结果偏高。

3 结 束 语

通过理论分析和数值仿真计算，分析了在相同的侵彻条件下不同截卵平台直径对初始侵彻弹道偏转的影响。仿真结果与理论分析结果得到的趋势一致，数值模拟结果基本相同。结果表明：截卵形头部侵彻产生的偏转力矩均为减小弹轴与靶标法线夹角，且截卵平台直径越大，弹头侵彻时产生的偏转力矩越大，偏转角速度增大；相同截卵平台直径下，随着头部形状系数的减小，偏转力矩和偏转角速度随之增大。

由于理论研究时作出部分假设，与实际情况存在一定偏差，如弹头侵彻是动态变化过程，而非单一状态过程，因此理论计算结果偏高。下一步工作重点是考虑弹头动态变化的理论模型精确描述。