双馈风机附加频率控制对系统调频动态的影响

张政，彭晓涛，李少林，梁恺，许饶琪，张锐

(1．武汉大学电气与自动化学院，武汉市430072；2.中国电力科学研究院有限公司，北京市 100192；3.合肥阳光智维科技有限公司，合肥市 230088)

0 引 言

双馈风电机组(doubly-fed induction generator based wind turbine,DFIG-WT)由于采用最大功率跟踪控制(maximum power point tracking，MPPT)模式，其转子转速与电网频率解耦，不能为系统提供类似于同步机惯性响应特性的动态频率支撑，因此大规模风电并网会削弱系统惯性，使系统在负荷扰动后产生更大的频率波动[1-2]。为改善双馈风机有功频率响应特性，使风机参与到系统频率控制中，双馈风机的附加频率控制策略得到了广泛的研究[3-5]，其中，利用组合频率微分和偏差信号实现风机惯性支撑和下垂控制的附加频率控制，成为改善风电系统频率响应特性的重要手段。但是这些附加控制在使风机具有频率支撑能力的同时，也对系统动态特性产生了一定的影响[6-7]。风机与系统通过有功调频产生相互作用的通道，从而可能使系统调频动态环节与双馈风电机组的多物理控制环节发生耦合作用，进而对系统负荷-频率控制的动态特性产生影响[8-9]。因此，有必要对双馈风机附加频率控制给系统调频动态带来的影响进行进一步研究。

近年来，已有很多文献围绕利用小干扰分析方法针对风机附加频率控制对系统小干扰稳定性的影响进行了研究。文献[10]采用阻尼转矩分析法，分析了双馈风机采用基于频率偏差的下垂控制对多机风电并网系统小干扰功角振荡的影响，以及双馈风机接入位置和同步机惯性时间常数与下垂控制对系统小扰动功角稳定影响特性的关系。文献[11-14]则研究了风电虚拟惯量控制对风电并网多机系统小干扰稳定性的影响。其中，文献[11]通过理论推导和基于DigSILENT仿真的特征值模态分析，研究了工作在MPPT模式下的双馈风电机组采用附加虚拟惯性控制对四机两区系统机电振荡模式的影响；文献[12]通过时域仿真，借助模式分析法研究了双馈风电机组采用基于频率微分反馈和基于变流器控制环节时间常数调整的附加虚拟惯量控制，以及控制策略不同控制参数对风电并网区域系统的发电机主导振荡模态小干扰稳定的影响；文献[13]研究了双馈风电机组锁相环动态与虚拟惯量控制对风机并网四机两区系统区间振荡模态的影响；文献[14]通过建立考虑锁相环动态的直驱风电机组虚拟惯性控制模型，针对锁相环振荡模态与系统机电模式在复平面分布位置的不同情况，利用特征值分析研究了虚拟惯性控制对系统机电振荡模式动态特性的影响。但是，用于这些影响研究的系统对象都没有考虑互联系统的调频动态特性，并且在反映风电机组多物理控制环节对系统小干扰稳定动态特性的耦合关系方面，由于考虑侧重点不同，并未对风电机组动态进行详细建模。此外文献[15]通过建立一次调频的直驱永磁风电系统小信号模型，基于特征值分析研究了不同风速下风电参与系统一次调频的小扰动稳定性，但也未研究对多机多区系统调频动态的影响。

基于上述分析，从分析双馈风机附加调频控制对互联系统负荷-频率控制动态特性的影响出发，同时考虑风电并网电力系统的运动模态通常由多动态环节耦合作用而成的特点[16-17]，本文通过建立详细描述双馈风机多物理控制环节耦合特性的状态空间模型，以及描述互联系统二次调频动态特性的数学模型，利用特征值模态和参与因子分析方法，研究风机附加调频控制对风机参与系统调频的小干扰稳定动态特性影响，并利用时域仿真验证理论分析结果的合理性。

1 考虑附加频率控制的双馈风机数学模型

1.1 双馈风电机组数学模型

DFIG-WT是利用双馈感应发电机(doubly-fed induction generator，DFIG)将风力机捕获的风能转换为电能的机组，与传统同步发电机不同的是，DFIG除定子与电网相连外，转子也经背靠背变流器与电网相连，其结构如图1所示。

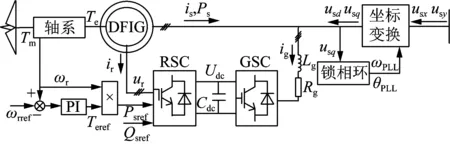
图1 双馈风电机组结构图Fig.1 Structure diagram of a DFIG-WT

DFIG-WT由DFIG、背靠背变流器及其直流环节、滤波电路、轴系等多动态物理环节，以及转子侧变流器(rotor side converter,RSC)控制、网侧变流器(grid side converter,GSC)控制、直流环节控制、锁相环控制、转速控制等多时间尺度控制环节构成[18]。各物理控制环节的数学模型如图1所示。图中，Tm、Te和Teref分别表示风电机组传动链轴系的机械转矩、电磁转矩及其参考值；ωrref和ωr分别表示发电机转子转速参考值和实际值；Ps和Psref分别表示定子输出有功及其指令值；Qsref表示定子输出无功指令值；ir和is分别表示发电机转子和定子绕组电流；ig表示GSC交流侧输入电流；Udc和Cdc分别表示变流器直流侧端电压和滤波电容；Lg和Rg分别表示GSC交流侧滤波电感和电阻；ur表示发电机转子绕组端电压；usd和usq分别表示风电机组并网点电压d、q轴分量；ωPLL和θPLL分别表示并网点电压的角频率和相位。

1)DFIG数学模型。

DFIG数学模型由同步旋转dq坐标系的电压方程和磁链方程组成。考虑感应电机的三相平衡，并不考虑磁链饱和效应和零序分量影响，将磁链方程代入电压方程，经整理可建立发电机四阶微分方程[19]，如式(1)所示。

(1)

式中：urd、urq和ird、irq分别表示RSC交流侧输出电压和电流的d、q轴分量；usd、usq和isd、isq分别表示发电机定子绕组电压和电流的d、q轴分量；Rs、Rr分别表示发电机定子和转子的电阻；Xss=Xs+Xm；Xrr=Xr+Xm；Xs表示定子绕组感抗；Xr表示转子绕组感抗；Xm表示定子和转子绕组间的互感抗；ωb和ωs分别表示基准角频率和系统同步电气角频率，且ωs=ω/ωb，当参考坐标系的旋转速度ω设置为ωb时，同步电气角频率与基准角频率相等；s为ωr与ωs之间的转差率。

2)变流器控制数学模型。

为实现双馈风电机组的变速恒频并网运行，DFIG转子需采用交-直-交变流器实现交流励磁控制。RSC根据DFIG输出有功和无功指令参考值Psref、Qsref，经比例-积分(PI)控制确定转子d、q轴电流分量参考值irdref、irqref，利用此电流参考指令经PI控制产生用于PWM控制的调制电压指令urdref和urqref，在为转子励磁绕组提供变频三相交流电压时，也分别利用q、d轴电压分量实现定子输出有功和无功的解耦控制。GSC利用直流环节端电压控制偏差，经PI控制产生交流侧输入电流d轴分量参考值igdref，利用定子端电压变化量产生输入电流q轴分量参考值igqref，再利用此2个电流参考值，经PI控制产生用于PWM控制的调制电压信号ugdref和ugqref，实现直流环节电容端电压恒定控制的同时，并可以利用无功调节阻尼定子端电压变化。上述RSC和GSC控制过程的数学模型分别如式(2)和式(3)所示。

(2)

(3)

3)轴系数学模型。

轴系数学模型用于描述连接风力机和感应发电机的转子角速度动态变化过程，通常可采用两质量块进行建模，其数学模型如式(4)所示。

(4)

式中：ωt为风力机转子机械角速度；ωr为发电机的转子转速；θ为轴系扭转角度；Ht为风力机的惯性质量常数；Hg为发电机的惯性质量常数；风力机和发电机的转子之间通过刚性系数为K、阻尼为D的弹簧轴连接。

4)转速控制数学模型。

转速控制用于产生定子输出功率指令，实现风电机组功率跟踪运行，其动态数学方程如式(5)所示。

(5)

5)直流环节数学模型。

直流环节数学模型主要用于描述电容端电压的动态变化过程，其数学模型如式(6)所示。

式中：ugd、ugq和igd、igq分别为GSC交流侧输入电压和电流的d、q轴分量；urd、urq和ird、irq分别为RSC交流侧输出电压和电流的d、q轴分量。

6)滤波电路数学模型。

滤波电路数学模型用于描述GSC动态调节输入功率时，GSC交流输入电流的动态变化过程，其数学模型如式(7)所示。

(7)

7)锁相环数学模型。

锁相环主要用于通过跟踪端电压相位来实现变流器与交流电网的同步,其同步dq坐标下的数学模型如式(8)所示[6]。

(8)

式中：kp7和ki7是锁相环的PI控制参数。根据由锁相环得到的相角θPLL，可将双馈风机的端电压由xy坐标系变换到dq坐标系，坐标变换的公式如式(9)所示。

(9)

式中：usx和usy是以αβ静止坐标系表示的风机并网点电压。

综合上述微分方程可知，DFIG-WT模型包括20个状态变量，分别为[isd，isq，ird，irq，x1，x2，x3，x4，x5，x6，x7，θ，ωt，ωr，x8，UDC，igd，igq，ωPLL，θPLL]。

现代大型风电场包含数量众多的风电机组，在研究中若采用包含每台风机及其控制模块的详细模型，不仅会増加运算的复杂程度，而且在利用特征值法进行小干扰稳定分析时可能会出现“维数灾”的问题。现有研究对这一问题的解决方法是先将风电场聚合等效为1台或少数几台等值风电机组，同时根据研究需要对模型的某些部分进行简化处理。本文同样利用聚合法将风电场中多台风机用1台等值风电机组代替，同时由于模型总体阶数不算太高，出于对模型准确性和计算精确度的考虑，未对风机进行进一步简化处理。

1.2 风电机组附加调频控制数学模型

由于双馈风机利用电力电子装置并网运行时，其功率跟踪运行方式使转子动能与电网频率变化解耦，无法为频率扰动提供转动惯量支撑和频率调节响应[3]。随着同步发电机被风电并网替代而退出运行，这种解耦也使电力系统的同步旋转惯量减少，对频率扰动时的惯量支撑能力减弱，因此风电机组的调频控制研究也日益受到关注。利用频率微分和频率偏差实现双馈风机惯性支撑和下垂控制的组合频率控制是一种典型附加频率控制方案[5]，如图2所示。该控制策略可使双馈风机在2种频率支撑时间尺度上发挥调频作用，从而改善风电并网系统的频率响应特性。

图2 双馈风电机组附加频率控制原理图Fig.2 Additional frequency control scheme of DFIG-WT

如图2所示，附加频率控制策略是根据电网频率f及其参考值fref的偏差在风电机组功率跟踪控制指令PsPPT上叠加惯量响应有功指令Pinertia和调频响应有功指令Pdroop，使风机在频率变化时能利用变桨减载、超速减载、转子动能等有功储备进行频率支撑的有功调节[20]。其中，Pinertia由频率偏差微分信号经比例环节kd确定，即：

(10)

Pdroop由频率偏差信号经下垂控制比例环节kp确定，即：

Pdroop=kp(f-fref)

(11)

数学模型表明附加频率控制给系统动态特性带来的影响主要体现在惯性响应的微分环节增加了系统的阶数，并通过引入新状态变量Δf而产生一个新的模态。同时，由于系统状态空间描述的输入系数矩阵元素值与状态变量稳态值有关，采用附加频率控制后，风机的有功指令值在频率扰动时与不采用附加频率控制时不同，因此状态变量稳态值的不同也会使采用附加频率控制前后的状态系数矩阵元素值不同，从而使求解的特征值也不同。

2 无附加调频的系统调频动态特性

为进一步分析频率扰动下的风电并网系统的调频动态特性，以及风机附加频率控制对其动态特性的影响，基于1.1节讨论的双馈风机数学模型和等值风电机组建模方法[21]，采用MATLAB/Simulink建立含双馈风机参与互联电力系统负荷频率控制调频动态数学模型，如图3所示。

图3 含风电互联电力系统调频控制原理图Fig.3 Frequency-regulation scheme of interconnected power system with wind power generator

模型中TG和TCH分别表示调速器和原动机一阶惯性响应时间常数；M表示同步发电机转子角动量，等于转子转动惯量J乘以同步电气角速度ω0；KD表示负荷的频率调节效应系数；B1、B2和R1、R2分别表示系统1、2的频率调节效应系数和等值发电机的频率调差系数；K和T都表示比例放大系数。由图3可见，依据前述风电机组状态空间模型建立的等值双馈风电机组接入互联系统1时，由于互联电力系统包含x21—x30所示的10个状态变量，因此图3所示含风电互联电力系统共包含30个状态变量，如表1所示。

图3中等值同步发电机和等值风电机组出力分别设为500 MW和300 MW，等值负荷设为1 300 MW，互联系统调频动态数学模型的相关参数和双馈风机参数参见附录A。采用MATLAB/Simulink的Control design toolbox对仿真模型在稳态运行时进行线性化，基于所得系统状态系数矩阵求解特征值，并利用复数特征值计算相应振荡频率和阻尼比，所得系统调频动态的运动模态分析结果如表2所示。结果表明，系统共有7对共轭复特征根和16个实特征根，分别对应7个振荡模态和16个非振荡模态。所有特征值均位于虚轴左侧，表明系统调频动态具有较好小干扰稳定性。

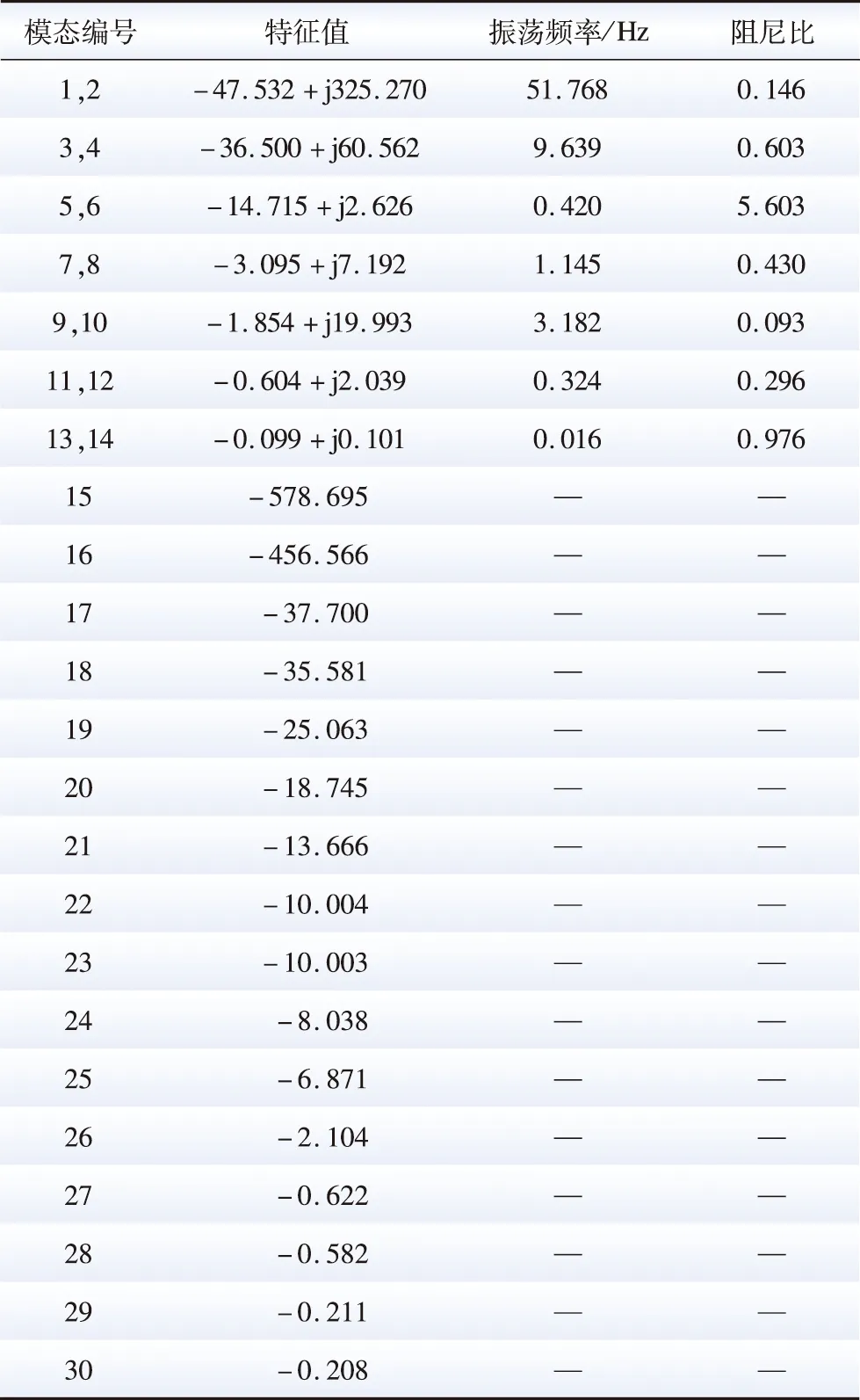
表2 无附加频率控制时系统调频动态的模态分析结果Table 2 Modal analysis results of frequency-regulation dynamic of power system without additional frequency control

进一步对各振荡模态的参与因子进行分析，所得结果如图4所示。

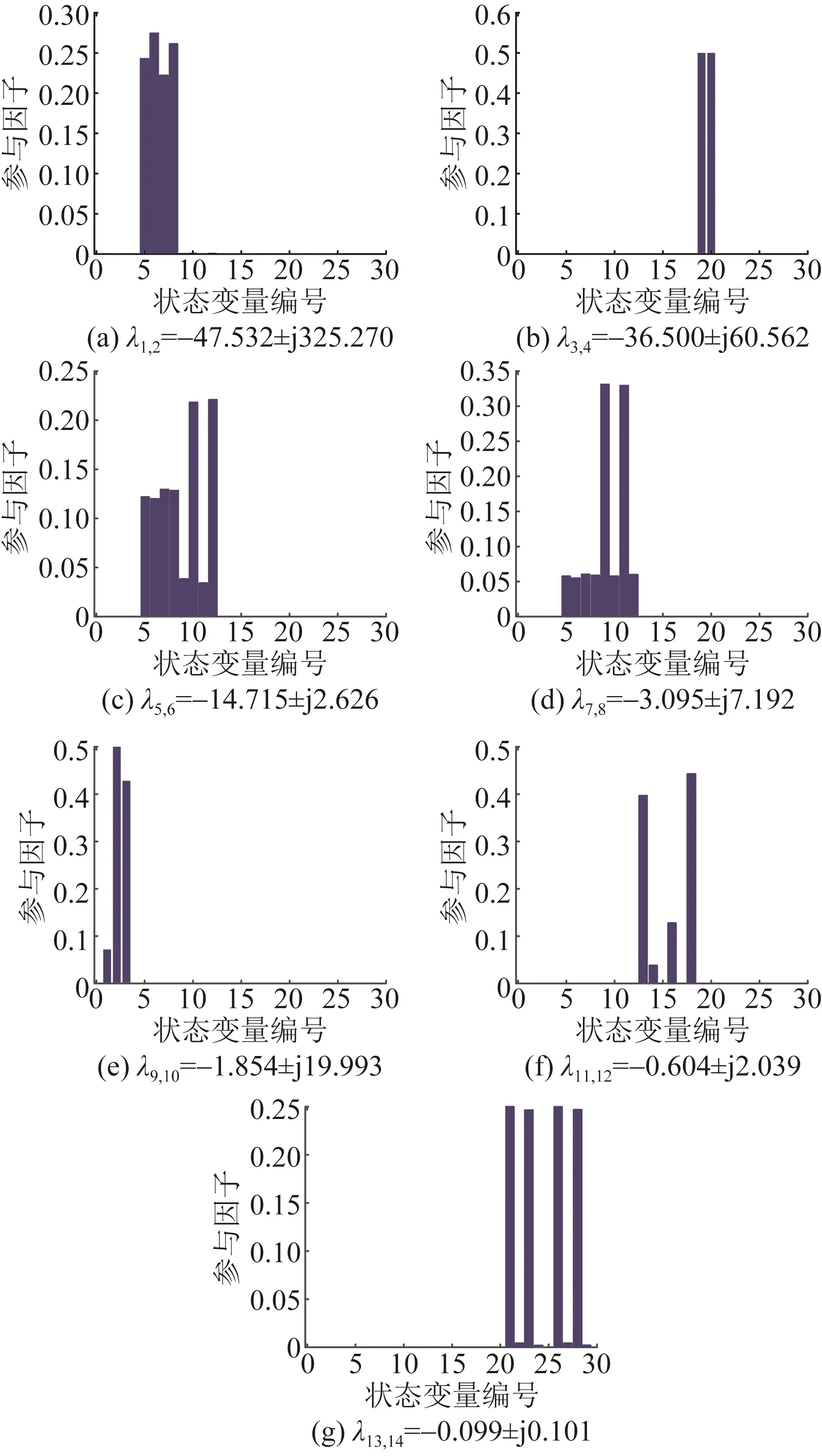
图4 振荡模态参与因子分析Fig.4 Participation factor analysis of oscillation modes

由图4中振荡模态的参与因子分析可见，λ1,2所确定模态的振荡频率是51.768 Hz，双馈感应发电机的状态变量[isdisqirdirq]是最大参与因子，表明该振荡模态由感应发电机转子和定子电流控制的相互耦合作用产生。λ3,4所确定模态的振荡频率是9.639 Hz，状态变量[ωPLLδPLL]的参与因子分析表明，该模态由锁相环动态主导。λ5,6和λ7,8的振荡频率分别是0.42 Hz和1.145 Hz，根据参与因子分析可知，2个模态分别是由RSC的无功和有功外环控制与感应发电机相互作用主导的低频振荡。λ9,10所确定模态的振荡频率是3.182 Hz，仅有轴系部分的3个状态变量[θωtωr]参与，属于轴系振荡。λ11,12所确定模态的振荡频率是0.324 Hz，状态变量[x5x6igdUdc] 的参与因子分析表明，该模态由滤波环节、直流环节和GSC相互作用的直流电压恒定控制产生。λ13,14所确定模态的振荡频率是0.016 Hz，是由互联系统调频动态相互耦合作用产生。并且风机与系统振荡模态的耦合作用环节相互独立，λ1—λ12所确定的6种振荡模态仅与双馈风机的状态变量相关，互联系统负荷-频率控制的振荡模态也仅与调频动态环节的状态变量相关，这也表明无附加频率控制的双馈风机接入系统，不会对互联系统负荷-频率控制的振荡模态产生影响，并且有功输出控制与系统频率变化解耦。对比各振荡模态的阻尼比可知，系统调频控制的小干扰稳定动态特性优于双馈风机的小干扰稳定动态特性。

系统16个非振荡模态的参与因子分析结果如表3所示。

表3 非振荡模态的参与因子分析结果Table 3 Participation factor analysis of non-oscillation modes

表3中，λ17、λ18、λ22、λ23、λ26和λ29所确定非振荡模态是仅由互联系统调频动态环节主导的模态，而其他非振荡模态都只与双馈风电机组的状态变量相关。分析结果同样表明，无附加频率控制的双馈风机没有对系统负荷-频率控制的非振荡模态产生影响。

根据各模态的参与因子分析的结果，总结了DFIG各组成物理控制环节耦合作用的调频运动模态，如表4所示。结果表明，感应电机与其他组成部分相比，在振荡模态和非振荡模态中的参与程度均较高，分别与51.768、0.42、1.145 Hz的振荡模态和2个非振荡模态存在耦合作用。因此在DFIG各组成物理控制环节中，感应电机对系统调频动态的影响作用最大。

表4 DFIG各组成环节对系统调频动态耦合作用的情况对比Table 4 Comparison of the dynamic coupling effect of each DFIG component on the system frequency regulation

3 有风电调频的系统调频动态特性

3.1 附加调频控制对调频动态的影响

将图3所示仿真模型的DFIG-WT采用图2所示附加频率控制，并设5 s时刻等值发电机1的有功负荷增加100 MW，双馈风机采用附加频率控制前后系统频率和风机输出有功的动态响应如图5和图6所示。

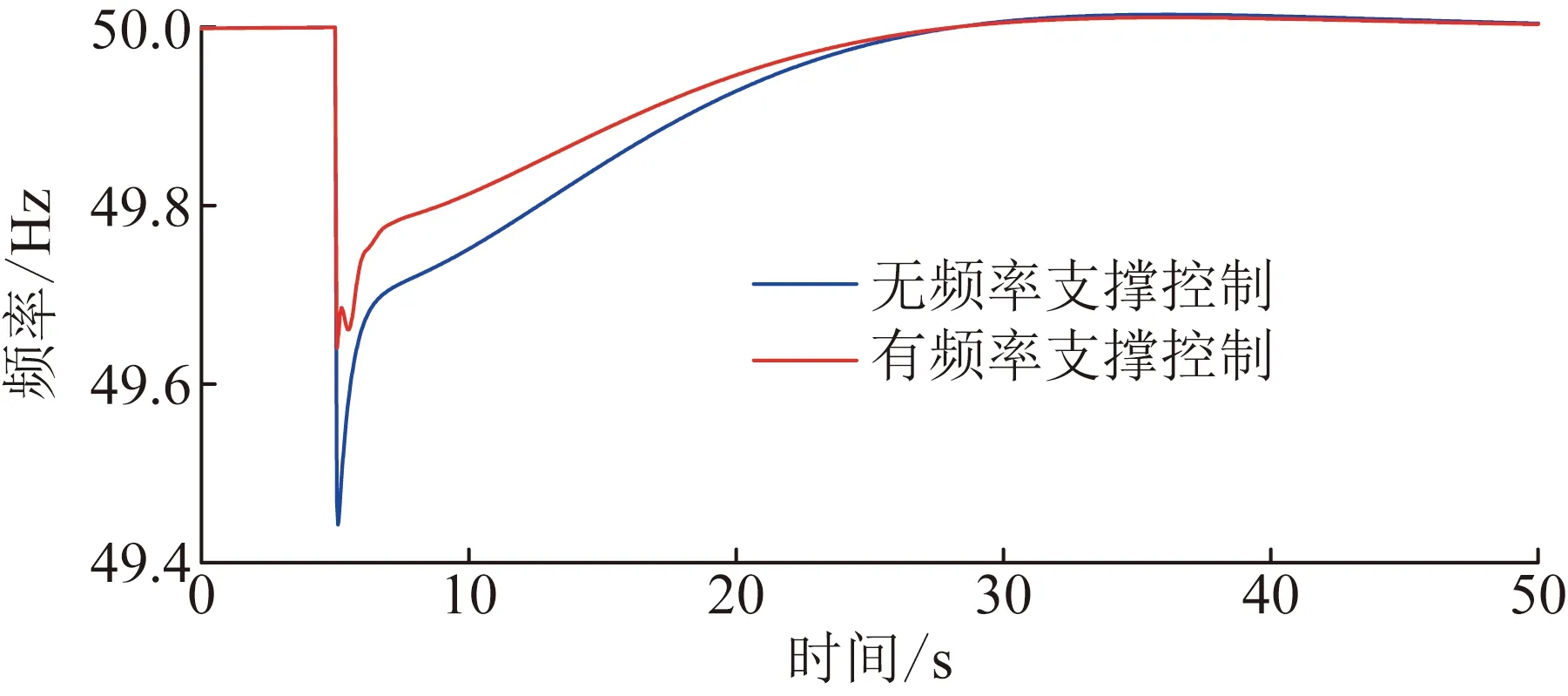
图5 DFIG-WT采用附加频率控制前后的系统频率响应Fig.5 System frequency response when DFIG-WT with or without additional frequency control

图6 DFIG-WT采用附加频率控前后的有功输出Fig.6 Output power of DFIG-WT with or without additional frequency control

对比结果验证了附加频率控制的有效性。图5的对比表明，采用附加频率控制后，系统的频率最低点从48.44 Hz提高到49.62 Hz，系统频率恢复稳态的动态过程对比说明附加控制在提高系统频率支撑能力的同时，也能够优化系统的频率调节特性。图6的对比则说明，附加频率控制能使双馈风机在频率扰动期间利用附加调频有功指令Pinertia和Pdroop增加有功输出，以提供惯量支撑和调频响应。

上述系统中，由于附加频率惯量支撑使系统引入了频率f作为新增状态变量x31，因此基于特征值分析得到的运动模态也增加为31个，如表5所示。

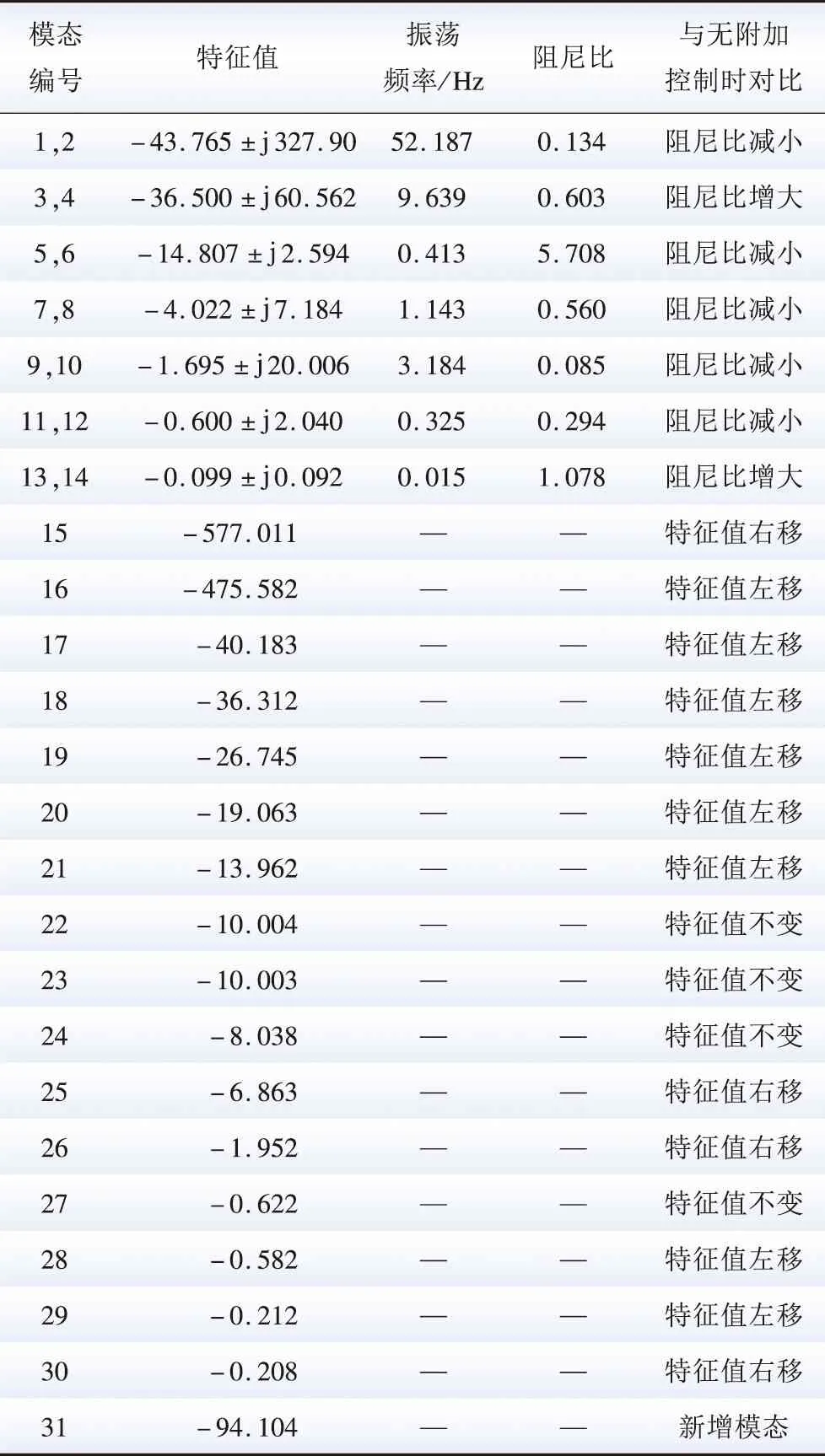
表5 有附加频率控制时系统调频动态的模态分析Table 5 Mode analysis results of frequency-regulation dynamic of power system with additional frequency control

与表2相比，风机附加频率控制的引入使系统负荷-频率控制动态增加一个特征值λ31=-94.104，并且此特征值在负实轴上离虚轴较远，其所对应非振荡模态将不会对系统负荷-频率控制的小干扰稳定动态特性产生影响。对比其他特征值，采用附加频率控制后所计算的特征值都在未采用附加频率控制时的特征值附近，说明附加频率控制虽然对系统各模态的小干扰稳定动态特性产生影响，但影响程度不明显。

对各模态进行参与因子分析可确定采用附加频率控制前后，各模态的耦合作用环节的变化。通过对比2.2节中各模态参与因子的变化可知，λ31、λ7,8和λ17所确定模态的参与因子发生变化。采用附加频率控制后，上述3种模态参与因子的分析结果如图7所示。其中，λ31是采用附加频率控制后新增的模态，由模态的耦合状态变量可知，该模态由惯量支撑控制、系统1的二次调频、双馈感应发电机定子转子有功电流分量控制相互耦合作用产生。

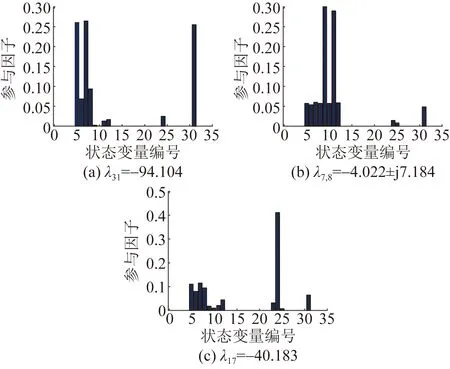
图7 λ31、λ7,8和λ17的参与因子分析Fig.7 Participation factor analysis of λ31,λ7,8 and λ17

对比图4和图7中λ7,8所确定模态的参与因子变化可见，附加频率控制使系统调频动态环节与风电机组动态环节发生耦合作用，对比阻尼比变化可知，该耦合作用使双馈风机的该振荡模态的小干扰稳定动态特性变差。而λ17所确定非振荡模态的参与因子表明，x31也具有一定的参与作用，并且该状态变量使双馈风机的感应发电机和RSC控制环节参与耦合作用，结合特征值在负实轴的位置变化可知，附加频率控制提高了该模态的动态稳定性。在其他模态中，因x31的参与因子接近于0，使附加频率控制在其他模态中没有使双馈风机的物理控制环节与系统调频动态发生耦合作用。图7仿真结果也同时表明，附加频率控制使风机对与其电气联系较强区域系统的调频动态产生影响，对电气联系较弱系统的调频动态则影响不大。

3.2 附加调频控制参数对动态特性的影响

在附加频率控制中，kd和kp这2个参数不仅会影响惯性支撑和下垂控制的作用效果，而且对风机动态特性也会产生影响，为此，基于参数摄动法进一步研究2个参数变化对调频动态特性的影响。

分别改变kd和kp研究特征值变化情况，小信号稳定性分析表明，系统特征值在参数大范围变化时变化情况较为复杂，不仅不同模态对参数变化的敏感度不同，而且不同模态的稳定性变化也不同。图8分别对比了模态7、8和模态1、2在保持kp=10、kd=1，振荡频率和阻尼比分别对kd和kp变化的响应。由图8可见，模态7、8的阻尼比在kd增加到12.04时减小为0，模态1、2的阻尼比在kp增加到1 327时减小至0，系统在此2种参数作用下达到临界稳定状态。分析结果也表明，附加调频控制参数的变化范围存在使系统保持稳定的限制。

图8 临界稳定附近的模态阻尼比和振荡频率变化Fig.8 Modal damping ratio and oscillation frequency variation near critical stability

在参数限定范围内，进一步研究各模态振荡频率和阻尼比对kd和kp小范围变化的响应灵敏度，以明确系统调频动态特性在参数设定值附近的稳定性。

保持kp=10，令kd以0.1的步长从0.1增加到1，系统7个振荡模态的振荡频率和阻尼比变化情况如图9所示。

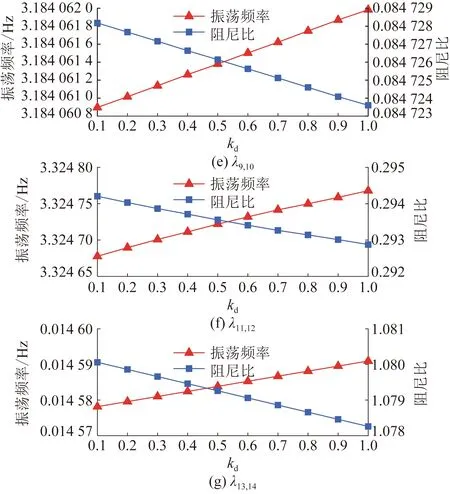
图9 λ1-14振荡频率和阻尼比随kd的变化Fig.9 Affection of oscillation frequency and damping ratio of λ1-14 with kd change

图9中，λ1,2和λ13,14所确定振荡模态的振荡频率和阻尼比随kd增大而分别增大和减小。λ5—λ8所确定振荡模态的振荡频率和阻尼比随kd增大而分别减小和增大。λ3,4所确定振荡模态的动态特性不随kd变化而变化，λ9—λ12所确定振荡模态的动态特性也对kd变化不敏感。

对于非振荡模态，选取仅与互联系统调频动态环节相关的6个模态，研究kd变化时附加频率控制对系统调频动态特性的影响。相关模态特征值变化情况如图10所示，图中红色和蓝色叉号分别表示加入附加频率控制前后的特征值。其中λ17、λ18、λ22、λ23、λ26所确定的模态，其特征值随kd的增大而向左移动，λ29所确定模态的特征值随kd增大而向右移动。

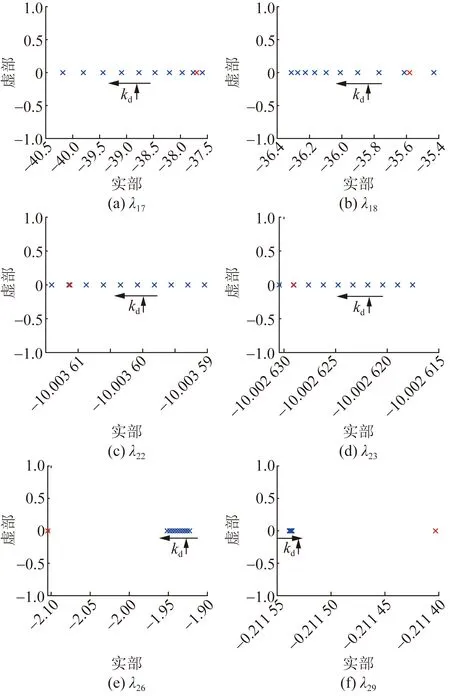
图10 部分非振荡模态特征值随kd的变化Fig.10 Affection of eigenvalues of part of non-oscillation modes with kd change

保持kd=1，kp以0.1的步长从1增加到10，系统7个振荡模态的振荡频率和阻尼比变化情况如图11所示。图11中，λ1,2和λ5,6所确定振荡模态的振荡频率和阻尼比随kp增大而分别增大和减小。λ7,8所对应振荡模态的振荡频率和阻尼比都随kp增大而增大。λ13,14所确定振荡模态的振荡频率和阻尼比随kp增大而分别减小和增大。λ3,4所对应振荡模态的振荡频率和阻尼比不随kp变化而变化。λ3,4所确定振荡模态的动态特性也不随kp变化而变化,λ9—λ12所确定振荡模态的动态特性也对kp变化不敏感。

图11 λ1-14振荡频率和阻尼比随kp的变化Fig.11 Affection of oscillation frequency and damping ratio of λ1-14with kp change

对于非振荡模态，选取仅与互联系统调频动态环节相关的6个模态，研究kp变化时双馈风机附加频率控制对互联系统调频动态特性的影响。相关模态特征值的变化情况如图12所示，图中红色和蓝色叉号分别表示加入附加频率控制前后的特征值。其中λ17、λ18、λ22、λ23、λ26所确定的模态，其特征值随kp的增大而向右移动，λ29所确定模态的特征值随kp增大而向左移动。

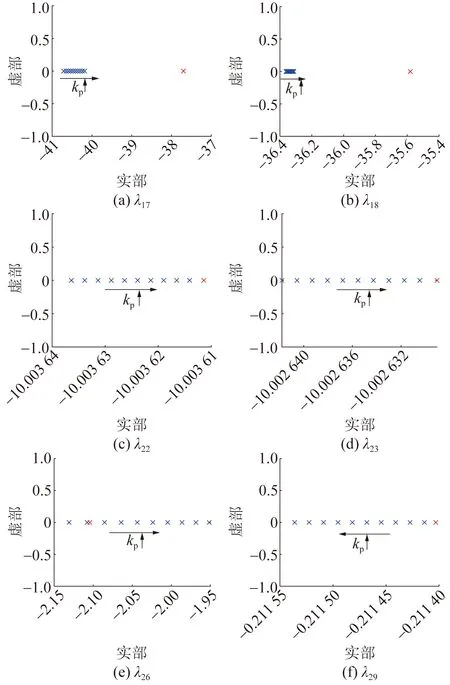
图12 部分非振荡模态特征值随kp的变化Fig.12 Affection of eigenvalues of part of non-oscillation modes with kp change

综上分析可见，kd和kp的参数变化对λ1,2和λ5,6所确定的双馈风机振荡模态、对λ13,14所确定的系统调频振荡模态、对λ7,8所确定的双馈风机和系统调频动态相互耦合作用振荡模态，以及部分非振荡模态的小干扰稳定动态特性都会产生影响。

3.3 时域仿真验证

分别在kd恒定、kp变化和kp恒定、kd变化2种情况下对图3所示系统进行时域仿真，并将风机有功输出与无附加频率控制时的情况进行对比，仿真结果如图13所示。在31个模态中，由于λ1,2所确定模态的耦合状态变量包括定子电流，因此风机输出有功的动态响应将反映该模态小干扰稳定动态特性对控制参数变化响应。由3.1和3.2节的分析可知，加入附加频率控制后，该振荡模态的阻尼比会随控制参数kd和kp增大而减小，图13的仿真结果验证了此动态特性的变化特点。

图13 风机输出功率动态响应Fig.13 Dynamic response of the output of DFIG

4 结 论

本文主要讨论了等值风电机组附加调频控制对区域系统调频动态特性的影响。在建立双馈风机详细状态方程基础上，研究了采用频率支撑控制风机对互联电力系统调频动态特性的影响。基于特征值模态分析和仿真验证，得到以下结论：

1)含双馈风机互联电力系统的负荷-频率控制包含分别由20个风机内部多物理控制环节和10个系统调频动态环节耦合作用形成的多个模态，其中包括7个振荡模态和16个非振荡模态，并且这些模态都具有小干扰稳定性。

2)由惯性支撑和下垂控制组成的双馈风机附加频率支撑控制能有效提高系统的调频动态特性，将系统受扰后的频率最低点提高0.18 Hz。虽然频率支撑控制对系统各模态小干扰稳定动态特性的影响不明显，但使双馈风机多物理控制环节和系统调频动态环节在特征值为-4.022±j7.184的振荡模态和特征值为-40.183的非振荡模态上发生耦合作用，并使系统调频动态增加一个特征值为-94.104的非振荡模态。

3)在所有振荡模态中，4个振荡模态的振荡频率和阻尼比对频率支撑控制的kd和kp参数变化具有较强敏感性，其余3个振荡模态对参数变化敏感性较弱。同时，部分非振荡模态的动态特性对频率支撑控制的参数变化也具有敏感性。

当研究多风场接入系统不同位置时，可先根据电气联系强弱对系统进行分区，再分别研究不同区域中风机附加控制对系统调频动态的影响。同时需要指出，模态分析结论仅针对本文提出的系统模型和运行工况，如何从理论角度将分析结论推广到其他系统和不同运行工况，是后续研究值得深入开展的工作。