考虑风电接入的电力系统鲁棒经济优化调度

邱革非,张鹏坤,贺漂

(昆明理工大学电力工程学院,昆明市 650500)

0 引 言

2020年中国风电产业发展大会在上海召开，会上指出高比例新能源是未来电力系统的发展趋势，预计到2030年，新能源装机占比将达38%，成为我国装机第一大电源。然而风电等新能源具有很强的随机性和波动性，随着电网中风电渗透率的提高，给电力系统安全可靠地供电带来了挑战[1]。

为应对风电不确定性给电网带来的影响，国内外学者做了大量的研究，解决办法主要有确定性方法、随机规划法和鲁棒优化法三种[2]。确定性方法通过预留机组旋转备用容量来消除风电波动的影响，文献[3]建立了多目标经济调度模型，但模型加入旋转备用容量对风电进行确定性处理，使得动态经济调度问题的解过于保守。随机规划法采用场景集[4]或机会约束[5]来描述风电的不确定性，但是在场景集的获取过程中计算量很大，且与实际情形存在误差；机会约束需要已知风电功率分布，而精确的风电功率分布很难获得。鲁棒优化采用不确定集合来描述风电的不确定性，具有明显的优势[6]。文献[7]建立了基于仿射可调节鲁棒优化法的鲁棒区间调度框架，实现风电容许区间最大化和发电成本最小化的目的；文献[8]引入储能系统，建立双层鲁棒区间经济调度模型，并采用两阶段迭代求解，提高了风电的消纳能力和系统运行经济性；文献[9]基于鲁棒优化蕴含的博弈思想，建立调度中心与风电场的双层主从博弈模型，并用最小风电区间削减量来优化风电出力区间；文献[10]通过设置最优弃风限制，建立了多时段鲁棒经济调度模型，优化得到安全的风电安全出力区间。

传统优化算法，如粒子群优化算法、遗传优化算法等，在处理此类模型时容易出现局部最优解、收敛速度慢等问题，而教与学算法是Rao等人于 2011 年提出的一种新的群体智能优化算法，具有收敛速度快、超参数量少等优点，在处理此类问题具有明显的优势[11-14]。

首先，本文通过引入弃风限制对风电场的风电出力预测区间进行优化，得到能够保证调度系统安全运行的风电安全出力区间；其次，在此基础上，建立了含有风电场的电力系统双层鲁棒区间优化调度模型，将调度中心看作调度上层，风电场看作调度下层，在提高系统调度可行性的同时，使得常规机组的运行成本和风电场的弃风成本最小；最后，研究了系统爬坡备用对风电安全出力区间的影响。由于考虑了常规机组的阀点效应，所建模型呈现非线性特点，本文采用改进的教与学优化算法与线性规划法相结合的求解方法对模型进行求解[15]。通过算例分析验证了所提模型和方法的有效性。

1 双层鲁棒经济调度模型

在传统的风电调度模式中，调度中心向风电场下达出力计划值，风电场则需要在出力允许的情况下严格地追踪该计划值[16]。这种调度模式存在明显的缺陷。一方面，受风电出力预测精度的影响，在实际调度过程中容易产生弃风；另一方面，当风电功率剧烈波动时，风机可能会产生极端的运行方式，威胁系统的安全运行，影响风机机组的使用寿命[17]。由于确定性风电功率预测值无法反映风电的波动性，区间预测成为当前最实用的风电功率预测方法，基于区间预测的鲁棒风电调度方法成为当前研究的热点[18-19]。在传统应用风电预测区间的多时段鲁棒经济调度中，必须保证风电在预测区间内的任意出力值都能使调度模型有解。然而受系统装机容量、爬坡备用等因素的影响，一般不能保证模型在任意时段均有解，因此需要对风电出力预测区间的边界进行一定的收缩，当收缩到一定范围时，就能保证调度模型有解[3]。

图1为本文所提双层鲁棒经济调度模型体系结构，首先风电场在日前向调度中心上报风电出力预测区间，调度中心根据各电厂的安全约束，风电预测数据以及负荷预测信息进行鲁棒区间调度决策，计算出收缩后风电场的安全出力区间和各火电机组的出力计划。然后调度中心将计算出的结果以调度指令下达给各电厂，最后风电场根据风电的安全出力区间进行出力控制，火电机组则根据出力计划调整出力。

图1 双层鲁棒经济调度模型Fig.1 Schematic diagram of two-layer robust economic dispatch model

1.1 上层优化调度

鲁棒区间调度模型根据火电机组和风电场的出力基态值进行经济调度，上层目标函数为燃料成本最小化。由于汽轮机的进气阀突然开启会使机组在耗量特性曲线上叠加一个脉动效果，即产生阀点效应，为更精确地描述机组的煤耗成本，本文考虑了机组的阀点效应。目标函数如式(1)所示：

|disin[ei(pt,i-pi,min)]|}

(1)

式中：T为调度周期的时段数；N为火电机组的台数；ai，bi和ci为火电机组的煤耗成本系数；pt,i为决策变量，代表火电机组i在t时段的出力基值；式中第4项为考虑火电机组阀点效应所产生的成本；di，ei为火电机组的阀点特性参数；pi,min为火电机组i的出力下限。

约束条件如下所示：

1)功率平衡约束。

(2)

(3)

式中：wt为风电场在t时段的出力基值；pload,t为调度系统在t时段的负荷预测值；ploss,t为系统在t时段的网络损耗，其计算方法如式(3)；Bij，B0i，B00为网络损耗的B系数矩阵。

2)火电机组的出力上下限约束。

pi,min≤pt,i≤pi,max

(4)

式中：pi,max，pi,min分别为火电机组i的出力上、下限。

3)火电机组的爬坡上下限约束。

-dri≤pt,i-pt-1,i≤uri

(5)

式中：uri，dri分别为火电机组i的爬坡上、下限。

4)风电场的出力约束。

(6)

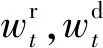
5)线路容量约束。

(7)

式中：Fl为第l条线路传输功率上限；πi,l为电源i对第l条线路的功率传输分布系数；Pm,load,t为负荷节点m在第t时间段内的有功需求。

1.2 下层优化调度

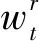
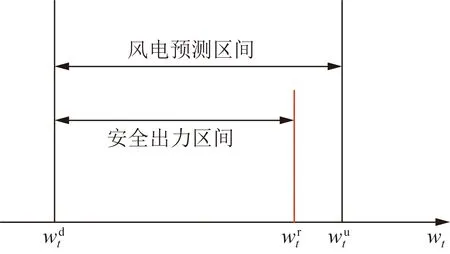
图2 弃风限制对风电出力预测区间的影响Fig.2 The influence of wind power curtailment on forecast range of wind power output

为了最大限度地减少弃风，下层模型以最小弃风成本为目标函数，如式(8)所示：

(8)

(9)

(10)

式中：λ为风电场的弃风惩罚系数；式(9)、式(10)分别为弃风限制约束和风电出力约束，其他约束条件与上层约束相同。

1.3 约束转化

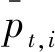
(11)

(12)

式中：αi,t为火电机组i在t时段所承担的风电场波动功率分配系数，且满足式(13)：

(13)

在实时调度情况下，火电机组和风电场的实时出力¯pt,i和wt均需满足与基值出力相同的约束，结合火电机组基值出力与实时出力之间的关系，约束条件式(4)、式(5)、式(7)可以转化为式(14)：

(14)

约束条件式(14)是关于不确定变量¯wt的线性约束，且式中系数均为常数，因此鲁棒优化的解在不确定变量的边界上求得，可以通过直接代入不确定变量边界的方法将不确定约束条件转化为确定性约束条件[20]。等价转换的思想主要是将一个含不确定变量¯wt的线性约束由式(15)表示：

(15)

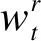
(16)

由此式(14)的等价约束为：

(17)

最终通过等价转换可以得到与原问题等价的确定性规划问题：

上层目标函数：式(1)；

约束条件：式(2)、(6)、(17)。

下层目标函数：式(8)；

约束条件：式(2)、(9)、(10)、(17)。

2 模型求解方法

本文采用改进的教与学算法和线性规划法联合对模型进行求解，教与学算法源于现实生活中的学习与教学行为，该算法包括以下两个阶段：

1)教学阶段。该阶段以教师教为主，在教学过程中，教师为学生中的最优个体，基于教师与全体学生平均水平的差距，通过教学不断提高学生的整体水平，如式(18)：

Pnew1,i=Pi+r(Ti-TFMi)

(18)

TF=round(1+r)

(19)

(20)

式中：Pi、Pnew1,i分别表示教学前后的学生知识水平；Ti为教师即种群中的最优个体；r为随机数且0≤r<1；TF为教学因子；round(x)表示对x四舍五入取整；Mi为学生在该阶段的平均水平；S为种群的总数。

2)学习阶段。在该阶段，由于各学生之间的知识差距，学生之间通过互相学习提高自身的知识水平，如式(21)：

(21)

式中：Pnew2，i表示该阶段更新后的学生知识水平；Pi1，Pi2为两个不同的学生的知识水平；(Pi1)，(Pi2)为学生的评价函数。

在常规的教与学算法优化过程中，无法在各科成绩中都选择最优学生，与本文模型中要求各个时段的机组出力均最优不吻合，因此本文对教与学算法进行了改进。调度周期含有T个时段可对应于学生的T门科目，分别在教学阶段和学习阶段中比较更新前和更新后学生的每一门成绩来更新学生，即比较更新前后每个时段的评价函数值来生成一个新学生，最终得到每一时段都是最优的机组出力组合。

在教学阶段，通过比较教学前后每个时段的评价函数来生成一个新学生，如式(22)：

Pn1,i(t)=argmin{f[Pi(t)],f[Pnew1,i(t)]}

(22)

式中：t为改进算法后所引入的时段；Pi(t)，Pnew1,i(t)分别为教学前后学生i在t时段的知识水平；f[Pi(t)]，f[Pnew1,i(t)]分别为学生i在进行教学前后t时段的评价函数；Pn1,i(t)为该阶段所生成新学生在t时段的知识水平。

在学习阶段，通过比较学习前后每个时段的评价函数来生成一个新学生，如式(23)：

Pn2,i(t)=argmin{f[Pi(t)],f[Pnew2,i(t)]}

(23)

式中：Pi(t)，Pnew2,i(t)分别为学习前后学生i在t时段的知识水平；f(Pi(t))，f(Pnew2,i(t))分别为学生i在进行学习前后t时段的评价函数；Pn2,i(t)为该阶段所生成新学生在t时段的知识水平。

然后对Pnew1,i和Pn1,i，Pnew2,i和Pn2,i分别执行约束处理策略，再与Pn1,i，Pn2,i比较适应度函数值更新学生知识水平，如式(24)、(25)：

(24)

(25)

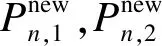
3 模型求解流程

基于改进的教与学优化算法和线性规划法相结合的方法对模型进行求解，求解流程如图3所示。流程图中Dmax为最大迭代次数。

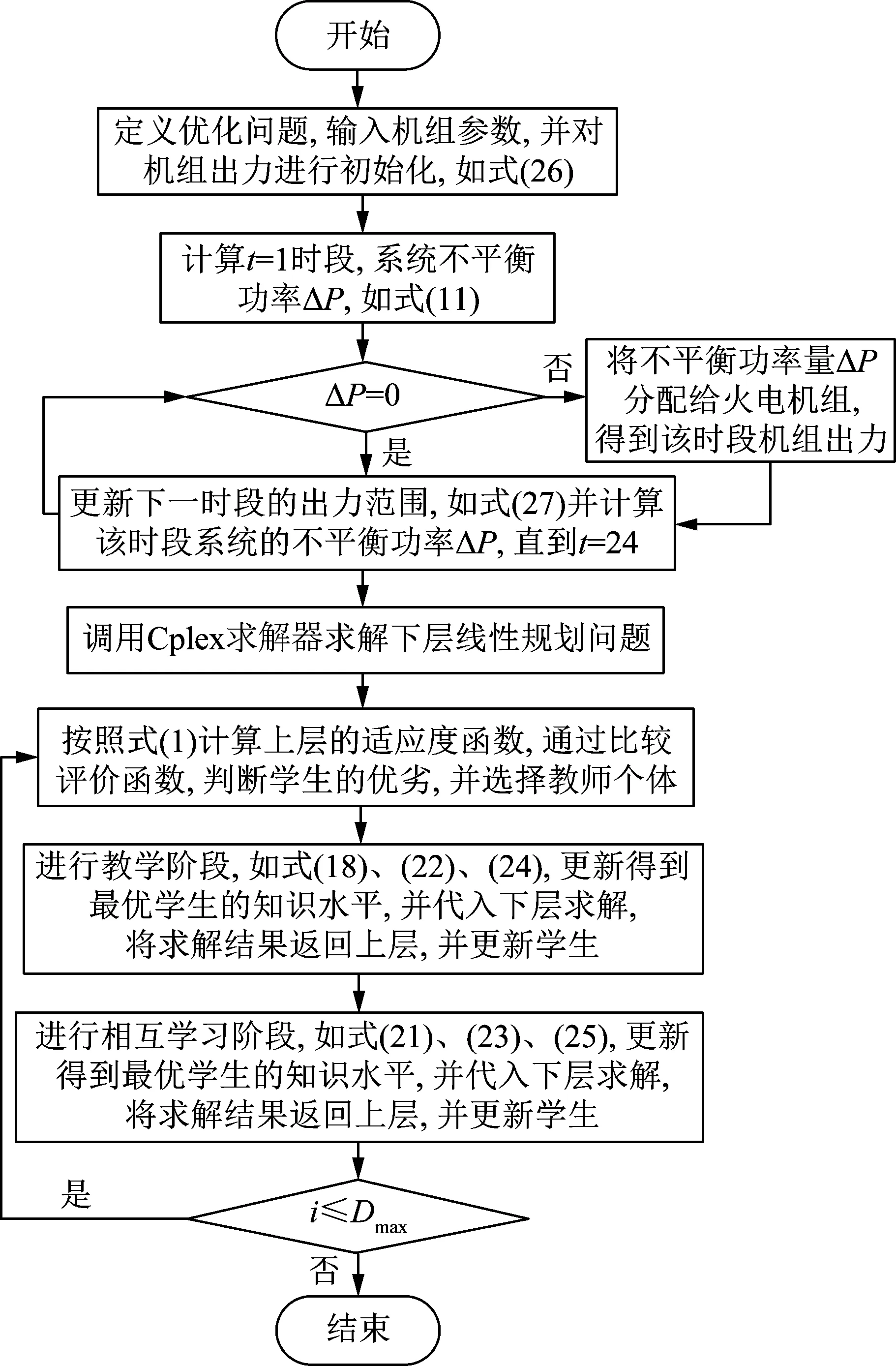
图3 算法求解流程图Fig.3 Flowchart of the algorithm solution

采用教与学优化算法求解问题时，首先需对班级进行初始化，即初始化火电机组出力和风电出力，如式(26)：

(26)

式中：r和rd均为0～1之间随机数。

然后判断系统功率是否平衡，并更新下一时段的出力范围，如式(27)：

(27)

4 算例分析

为了验证双层鲁棒经济调度模型和所用算法的优越性，在改进的10机系统中对算例进行分析，调度周期为24h，调度时段为1h，系统预测负荷如图4所示，网损系数参考文献[21]，且在调度周期内网损系数为定值。算例设定如下：

图4 系统日负荷预测曲线Fig.4 Forecast curve of daily system load

算例1：该算例只包含10台火电机组，各机组参数如附表A1所示，计及火电机组的阀点效应和系统网损。

算例2：在该算例中，将算例1中的机组6用容量为600 MW的风电场替代，风电场的预测区间数据见附表A2，其他条件与算例1相同。

4.1 模型求解结果及分析

采用改进的教与学优化算法与线性规划法联合对算例1和2进行求解，求解结果见表1，机组各时段最优出力见图5、图6。

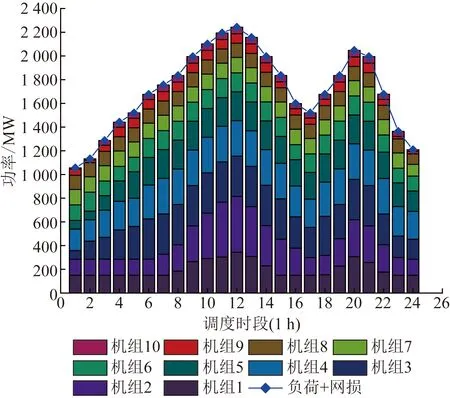
图5 算例1机组各时段出力计划Fig.5 Unit output plan for each period in Case 1

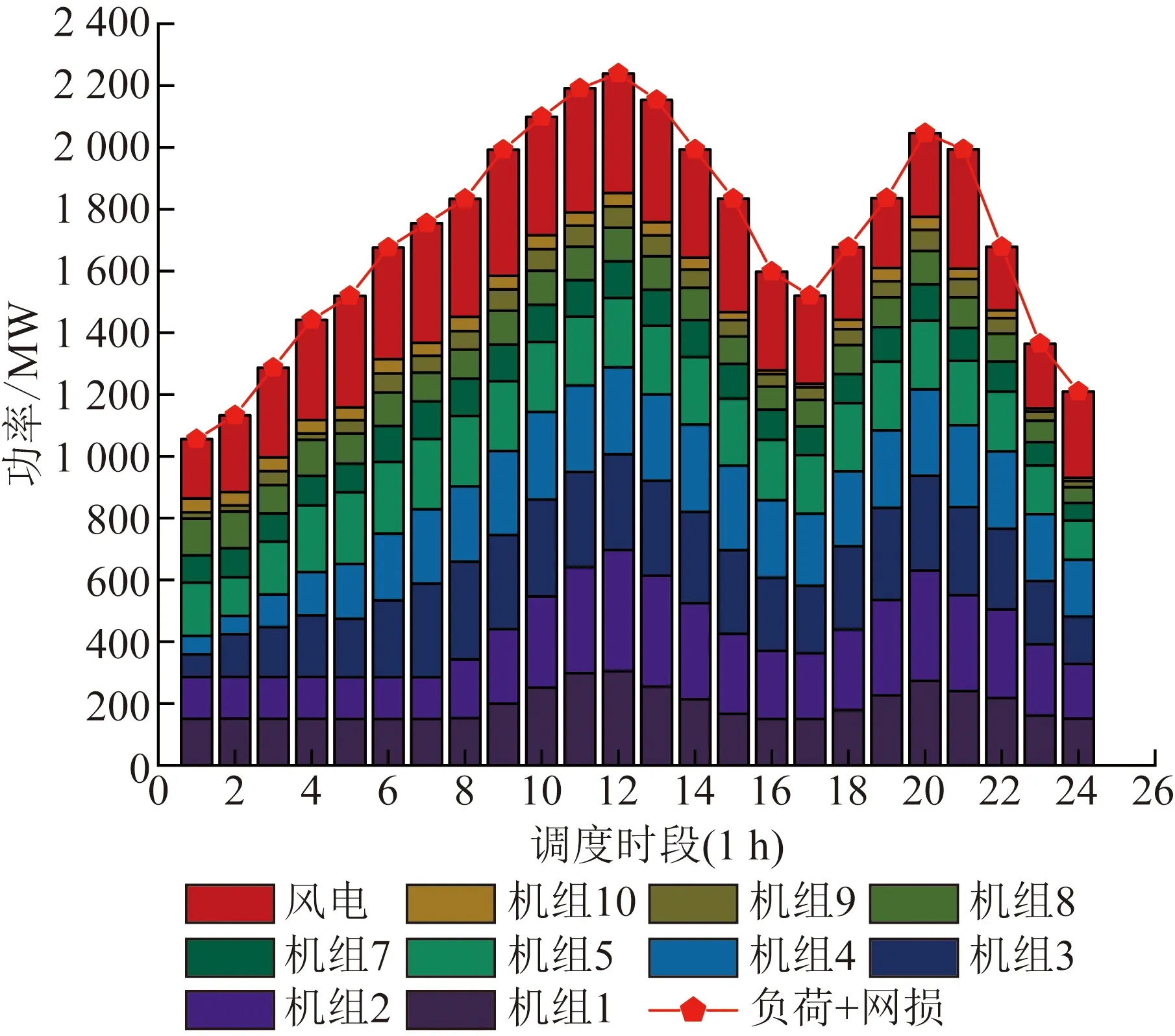
图6 算例2机组各时段出力计划 Fig.6 Unit output plan for each period in Case 2

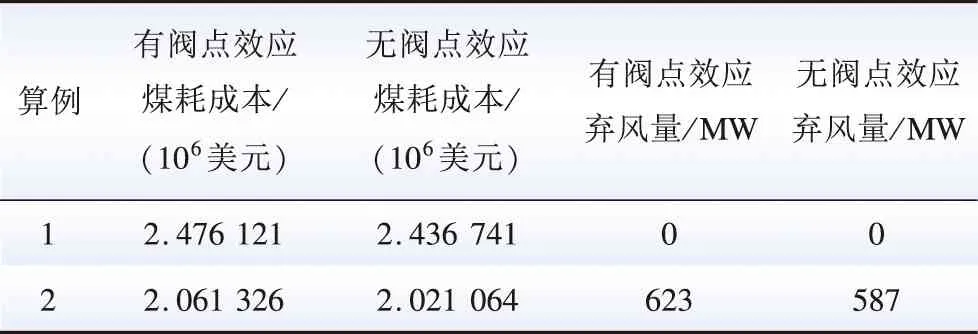
表1 有无阀点效应求解对比结果Table 1 Comparison results with or without valve point effect

从表1中可以看出，当风电并入电网后，火电机组的煤耗成本明显降低，风电的加入有利于实现节能减排和电网运行经济性。由于风电波动和系统备用不足等，系统无法按照风电的预测区间进行发电，需要对风电的预测区间进行削减和风电场弃风，弃风量为623 MW；考虑火电机组阀点效应较不考虑阀点效应的机组成本高1.61%；考虑火电机组阀点效应较不考虑阀点效应的弃风量高6.12%。

采用所提方法对算例2求解，得到如图7所示的风电安全出力区间。

由图7可以看出在调度周期的第16时段，第22至24时段，风电的安全出力区间上限低于预测区间的上限，表明风电在该时段波动较大，系统所能提供的爬坡备用无法满足系统所需爬坡备用，因此需要对风电出力预测区间进行收缩，风电场产生弃风。

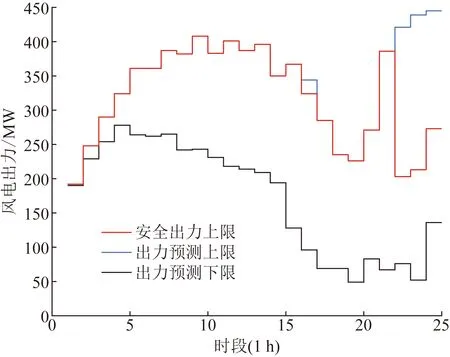
图7 算例2的风电安全出力区间Fig.7 Safe output range of wind power in Case 2

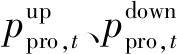
(28)

(29)

(30)

(31)

运用式(28)—(31)计算算例2各时段上下爬坡备用供给量与需求量，结果如图8、图9所示。

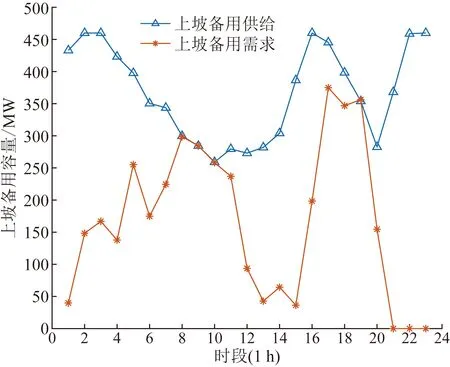
图8 上坡备用供需对比Fig.8 Comparison results between supply and demand for upward ramping reserve

由图8、图9可以看出，在调度周期内有些时段的上坡备用或下坡备用需求为0，这表明在该时段内负荷上升或下降较快，虽然有风电波动影响，但是火电机组仍要较大幅度地增加或减少出力来保持系统功率平衡。若负荷上升较快，则下坡备用需求为0，若负荷下降较快，则上坡备用需求为0。算例2中系统上下坡备用容量需求均不大于供给量，因此在调度周期内，系统均可保持安全运行。而某些时段系统上下坡备用容量需求等于供给量，即系统处于临界状态，则要求风电出力不能超过安全区间，否则会导致系统不稳定。

图9 下坡备用供需对比Fig.9 Comparison results between supply and demand for downward ramping reserve

4.2 求解方法的有效性验证

为验证文中所提求解方法的有效性，选择算例1中的10台机组进行测试，对改进的教与学算法与其他算法进行比较，其中教与学算法的群体设为50，迭代次数为300，粒子群算法学习因子设置为c1=c2=2，迭代次数为300。对比结果见表2。

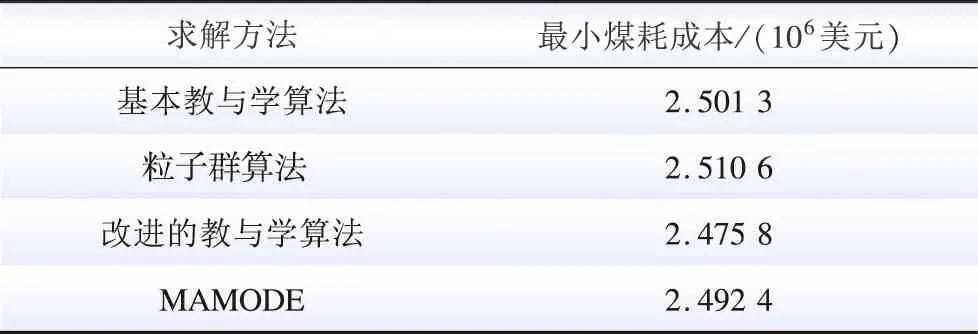
表2 不同求解方法煤耗成本Table 2 Coal consumption cost of different solution methods

从表2可看出，与其他方法相比，采用改进的教与学算法求解得到的煤耗成本更低，更有利于电力系统实现经济调度，符合国家的节能减排政策。

5 结 论

为应对风电接入给电力系统运行带来的挑战，本文提出一种双层鲁棒经济调度模型，并引入弃风限制收缩风电出力预测区间，保证风电在安全出力区间内的任意出力值都能使调度系统安全可靠地运行。算例分析表明：

1)由于考虑了火电机组的阀点效应，采用改进的教与学算法与线性规划法联合对模型进行求解，证明了求解方法的有效性，且考虑阀点效应较不考虑阀点效应的机组成本高1.61%。

2)通过引入弃风限制对风电出力预测区间进行收缩，得到了在任意时刻均能保证调度系统安全运行的风电安全出力区间，并且验证了爬坡备用的充足与否是风电安全区间的主要影响因素。