底盘构件多轴随机载荷下高周疲劳准则研究
董国疆 张 猛 魏留伟 张永强
1.河北省特种运载装备重点实验室(燕山大学),秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,066004
0 引言
汽车零部件疲劳可靠性是评价汽车的重要指标之一[1]。对汽车底盘结构件而言,绝大多数疲劳失效发生在随机载荷下[2],而随机载荷下的疲劳分析不同于恒幅载荷下的疲劳分析,随机载荷下的零件会呈现多轴应力状态。虽然关于构件多轴疲劳寿命预测已有较为深入的理论研究,但将这些理论应用在汽车构件寿命预测和分析的研究却鲜有报道,主要原因有:疲劳失效发生的特定平面不易获取,多轴疲劳加载下材料平面上的剪应力/应变幅值等参数值的确定方法研究较少[3]。为更准确地预测汽车零部件寿命,研究多轴疲劳准则在车辆领域的应用尤为重要。
国内外对零部件耐久性预测准则开展了诸多有益的研究。刘俊等[4]使用虚拟迭代的方法提取驾驶室悬置处和翻转机构处的载荷谱,在nCode软件中使用基于静强度理论的等效应力/应变的方法进行寿命计算,与台架强化试验寿命相比,误差在28.1%以内,该方法提取载荷准确,但未考虑多轴受力对疲劳寿命的影响。刘海燕等[5]通过对曲轴进行瞬态分析得到危险点应力信息,然后使用基于静强度理论的von Mises等效应力与基于最大剪应力幅平面的McDiarmid准则计算曲轴疲劳损伤,通过对比得出McDiarmid准则从裂纹萌生和扩展的机理上来说更合理,该研究还介绍了随机载荷下疲劳分析的流程,将最大剪应力幅平面的选取进行了简化,但对大部分随机载荷并不适用。钱立军等[6]通过道路模拟试验得到轮胎激励,结合多体动力学模型得到下摆臂连接点载荷谱,使用Wang-Brown多轴疲劳模型对下摆臂进行疲劳分析,并与路试情况进行对比,仿真与实验结果表明,下摆臂的最危险位置接近,且该位置处的疲劳寿命也十分接近。GAO等[7]对Zhang-Yao准则在频域内重构并进行了多轴随机寿命载荷下的寿命预测,通过与试件实验结果对比可得预测结果大部分处于两倍分散带内,此外在计算最大剪应力幅平面时发现,在时域内使用最小外接圆法,在频域内则要采用基于频域的方法进行计算。KASHYZADEH等[8]、SHARIYAT[9]使用McDiarmid准则、Findley准则、Dang Van准则等多种高周疲劳准则计算转向节与稳定杆在随机载荷下的疲劳寿命,与实验数据对比并从预测精度方面评估每种准则,但未明确说明随机载荷下临界平面的选取方法。
当前研究汽车零部件疲劳寿命侧重于使用基于静强度理论的等效应力/应变法,即使应用多轴疲劳准则也多是简单载荷下的寿命计算。本文以转向节为研究对象,使用基于静强度理论的von Mises高周疲劳准则与基于临界平面的C-S准则、McDiarmid准则等七种高周疲劳准则计算转向节随机载荷下的疲劳损伤,并分析临界平面准则中基于的最大剪应力幅平面、最大损伤平面和第一主应力最大值平面三种临界平面在随机载荷下的计算方法,然后从等效应力幅分布、预测寿命、计算成本三个方面对准则进行分析评估。
不同高周疲劳准则以临界点的应力状态为计算的基础数据,通过统计得到临界点的幅值分布与寿命预测规律。虽然在相同路段下汽车不同底盘部件的应力幅范围不同,但是应力分量之间的比例关系具有相似性。本研究以试验场采集到的典型强化路载荷谱为原始数据,同时转向节属于典型的底盘部件,因此统计得到的规律对汽车底盘部件具有适用性。
1 多轴高周疲劳准则理论
目前使用广泛的多轴高周疲劳准则包括von Mises准则、McDiarmid准则[10]、Dang Van准则[11]、Zhang-Yao准则[12]、Findley准则[13]、C-S准则[14]。
(1)von Mises准则。von Mises准则是目前对汽车零部件寿命预测应用最广泛的准则,此准则要求计算点的各应力分量时间历程为同频率、零均值且无相差时计算结果才相对准确,其等效应力幅表达式为
(1)
其中,σa,von为von Mises准则等效正应力幅;Δσij(i,j=1,2,3)为各应力分量变程。应力幅为应力变程的一半,计算随机载荷下疲劳寿命时通常用下式进行等效:
(2)
其中,σij(i,j=1,2,3)为各应力分量;Δ(·)表示计算整个等效应力时间历程的变程函数,即首先计算等效应力时间历程,再进行循环计数获取等效应力幅。这样虽然会使计算结果的准确性降低,但不需要计算与考虑各应力分量变程与相位差的影响,更加便于应用,所以被广泛采用。
(2)Carpinteri-Spagnoli准则(C-S准则)。C-S准则为二维应力场下的von Mises准则的扩展形式,认为法向应力平均值会降低金属材料的抗疲劳性能,所以需要对正应力幅进行平均应力修正。通过将多轴非比例应力转化为单轴零均值应力进行损伤计算,其等效应力幅表达式为
(3)
其中,σa,C-S为C-S准则等效正应力幅;σaeq为经平均应力修正后的等效正应力幅;τa为剪应力幅;σ-1、τ-1分别为应力比R=σmin/σmax=-1时的拉伸和扭转疲劳极限,σmin、σmax分别为循环载荷下的最小应力和最大应力;σm为正应力均值;σa为正应力幅;σu为强度极限。
(3)McDiarmid准则。目前McDiarmid准则在多轴疲劳方面的应用较多,它兼顾了便捷性与准确性,几乎是一种单参数的临界面准则,其等效应力幅表达式为
(4)
其中,τa,McD为McDiarmid准则等效剪应力幅;τ-1,AB为出现A型裂纹和B型裂纹对应的单轴纯扭加载下的疲劳极限,A型裂纹沿着试件表面扩展,B型裂纹由试件表面向内部贯穿,对于拉-扭加载,一般发生A型裂纹[15],有τ-1,AB=τ-1;σn,max为最大正应力。
(4)改进的McDiarmid准则。SHARIYAT[16]研究发现,当法向应力的阶数远高于剪应力的阶数时,McDiarmid准则预测寿命会变得不准确,因此需对其进行改进,改进后的McDiarmid准则可表示为
(5)
其中,τa,McD_1为改进后的McDiarmid准则等效剪应力幅。
(5)Dang Van准则。Dang Van准则是一种双参数准则,该准则在定义等效应力时考虑了静水应力σH(σH=(σx+σy+σz)/3,σx、σy、σz为3个正应力分量)的影响,是依据剪应力幅和最大静水应力而构造出的多轴高周疲劳破坏准则,可表示为
(6)

(6)Findley准则。Findley准则提出临界平面内的正应力最大值与剪应力幅值可以作为疲劳评估的基本参量,该准则被认为比其他临界面准则更加准确,其等效应力幅表达式为
(7)
其中,σa,Fin为Findley准则等效正应力幅。
(7)改进的Findley准则。SHARIYAT[16]改进了Findley准则,并通过对汽车某零部件进行试验研究发现,改进后准则的寿命预测更加准确[19],其表达式为
(8)
其中,τa,Fin_1为改进后的Findley准则等效剪应力幅;k为正应力在疲劳损伤中所占的比重。
(8)Zhang-Yao准则。Zhang-Yao准则以临界面上最大剪切应力幅和最大法向应力的非线性组合为损伤控制参数,考虑了平均应力的影响,对临界面上正应力与剪应力进行了平均应力修正,开展了多轴非比例加载实验,对比结果表明该模型的预测准确性较好,其表达式为
(9)
其中,τa,Z-Y为Zhang-Yao准则等效剪应力幅。
在以上8种多轴疲劳准则中,McDiarmid、Dang Van、Findley等准则最初是用来校核零件是否满足无限寿命的,而不是用于寿命估计,但通过对载荷时间历程进行循环计数,结合损伤累计准则,这些准则越来越广泛地应用于计算构件的疲劳寿命。
当前研究普遍认为剪应力的平均值对材料疲劳性能没有影响,然而DAVOLI等[20]通过对某些材料进行实验研究发现,当最大剪切应力低于剪切屈服强度时,平均剪切应力会明显缩短疲劳寿命,并且计算累积损伤通常使用R=-1时的S-N曲线与T-N曲线,因此本研究考虑平均正应力与平均剪应力的影响,对上述准则中的正应力幅与剪应力幅均进行了平均应力修正。
2 强化路载荷采集与转向节模态分析
2.1 试验场载荷采集
实验车辆为某品牌B级轿车,该车整备质量1538 kg,轴距2796 mm,前悬架为麦弗逊悬架,后悬架为多连杆悬架。根据试验场耐久性试验行驶规范,采样频率设定为1000 Hz,采集不同工况下的轮心六分力信号、轮心与车身加速度信号,在虚拟迭代过程中需要将轮心六分力作为迭代目标,将轮心与车身加速度作为监测信号。对实测信号进行去漂移、去毛刺、滤波、重采样处理。本文重点采用典型随机强化路石块路乙(图1)为研究对象,该路段对底盘零件形成的损伤较为明显。

图1 试验场载荷谱采集Fig.1 Collection of load spectrum in test field
2.2 转向节模态分析与验证
在CATIA软件中通过点云逆向的方式建立转向节有限元模型,对转向节受力与疲劳进行分析前需要进行自由模态分析与验证,以确定所建立的模型是否符合使用要求。将模型导入HyperMesh软件中进行3D网格划分并检查网格单元质量,模型材料的属性见表1。对转向节进行自由模态仿真,提取前6阶固有频率。如图2所示,设计转向节实体零件自由模态试验,使用橡胶软绳悬吊转向节来模拟自由状态。使用单点激励多点响应的锤击法测量转向节模态参数,由于模态仿真得到的固有频率不超过3200 Hz,因此为保证模态试验能够采集到最高阶固有频率,设置采样频率为10 kHz。由仿真与实测得到的前6阶固有频率(表2)可以看出,两者的相对误差不超过10%,所以转向节有限元模型符合分析精度要求。

表1 转向节材料属性Tab.1 Material properties of knuckle

图2 转向节自由模态试验Fig.2 Free modal test of steering knuckle

表2 转向节自由模态固有频率试验与仿真对比Tab.2 Comparison of test and simulation free mode natural frequency of knuckle
3 转向节特征点的载荷及应力分量提取
3.1 转向节连接点载荷提取
在汽车行驶过程中,转向节主要受到减振器、车轮中心、转向横拉杆和下摆臂传递来的力,对转向节进行仿真分析时,需要将各连接点的力施加于有限元模型对应的节点上,连接点信息见图3。由于试验场只能采集到轮心受力,其他连接点的受力难以采集,因此需要使用虚拟迭代提取连接点载荷时间历程。虚拟迭代法只需采集轮心载荷并将其作为车辆多体动力学模型输入激励,采集车身和悬架关键点作为监测信号,从而提取悬架零部件载荷谱[15]。虚拟迭代精度可由相对损伤和均方根值(RMS)相对误差进行校验,当相对损伤值在0.5~2之间或RMS相对误差在20%以内时认为迭代精度满足要求。本次整车轮心六分力(包括三方向力Fx、Fy、Fz以及三方向力矩Mx、My、Mz)迭代过程中的相对损伤值变化趋势如图4所示,可以看出,迭代至第6次时,六分力的相对损伤值均介于0.8022~1.1613之间。图5为提取的石块路乙路段下转向节4个连接点共12条载荷时间长度为82 s的时域载荷曲线,对应位置与方向见图3。

图3 转向节有限元及连接点信息Fig.3 Steering knuckle finite element and connecting point information

图4 左前轮心六分力迭代相对损伤变化曲线Fig.4 Relative damage curves of six-component force iterative of left front wheel center
3.2 临界点应力分量提取
转向节的寿命取决于零件上最薄弱位置的耐疲劳破坏能力,所以首先需要找到疲劳热点,然后分析其载荷循环次数进而判定零件寿命。在汽车行驶过程中转向节各连接点承载状况复杂,因此进行力学分析时引入惯性释放法,即使用零件的惯性(质量)力来平衡外力。在Hypermesh软件中对转向节4个连接点分别在x、y、z三个方向上施加1 N的单位力,共12种载荷工况,进行惯性释放分析后得到.op2文件。
疲劳热点分析在nCode 13.0软件中进行,导入.op2文件与12条时域载荷曲线(图5),并对模型赋予材料属性,使用von Mises等效应力进行疲劳损伤分析。经分析可得到转向节寿命值最小的节点(编号3731)位于图6所示的危险区域。

(a)力F1 (b)力F2 (c)力F3 (d)力F4

图6 von Mises应力下疲劳仿真Fig.6 Fatigue simulation under von Mises stress
基于临界面的损伤模型均需要提取临界面上的正应力与剪应力,而正应力与剪应力需要根据寿命值最小节点处的应力分量计算得到。试验车辆在石块路乙路段行驶过程中,转向节处于弹性变形内,且通过对轮心六分力进行频谱分析可得频率范围均在50 Hz范围内,远小于模态试验中第一阶固有频率1290.99 Hz,满足这两个条件即可使用准静态法对转向节进行动载仿真分析[21]。在ABAQUS软件中对转向节对应节点施加提取到的时域载荷谱并进行动载响应分析,最终可提取得到危险点处的6条应力分量曲线,见图7。
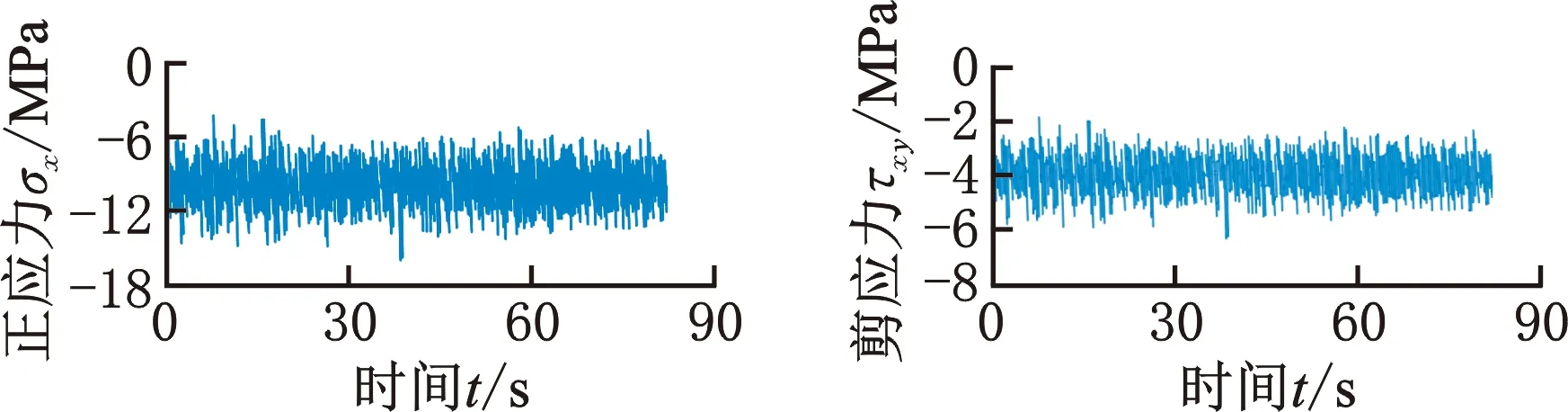
(a)正应力σx (b)剪应力τxy
4 临界面选取与多轴循环计数
4.1 临界面法简介
临界面法认为承载零件结构中某一给定损伤参数达到最大的平面往往是结构疲劳失效的平面,这个平面也常常出现裂纹的萌生和扩展。由于临界面法评定结构疲劳寿命过程的物理意义更加明确,寿命预测结果更加准确,因此已得到了广泛的应用[22]。如图8所示,将承载零件某一节点的应力状态在不同平面上分解,会得到不同的正应力与剪应力结果,平面方向由其法线方向的单位向量l=(sinθcosφ,sinθsinφ,cosθ)表示,其中θ为法线与z轴的夹角,φ为法线在Oxy平面的投影向量与x轴的夹角,且0°≤θ<180°,0°≤φ<180°,若O点的应力分量为
(10)
则此时正应力为
σ=lσijlT
(11)
全应力S沿坐标轴三个分量为
(Sx,Sy,Sz)=lσij
(12)
全应力与剪应力分别为
(13)
(14)
4.2 不同准则的临界面选择
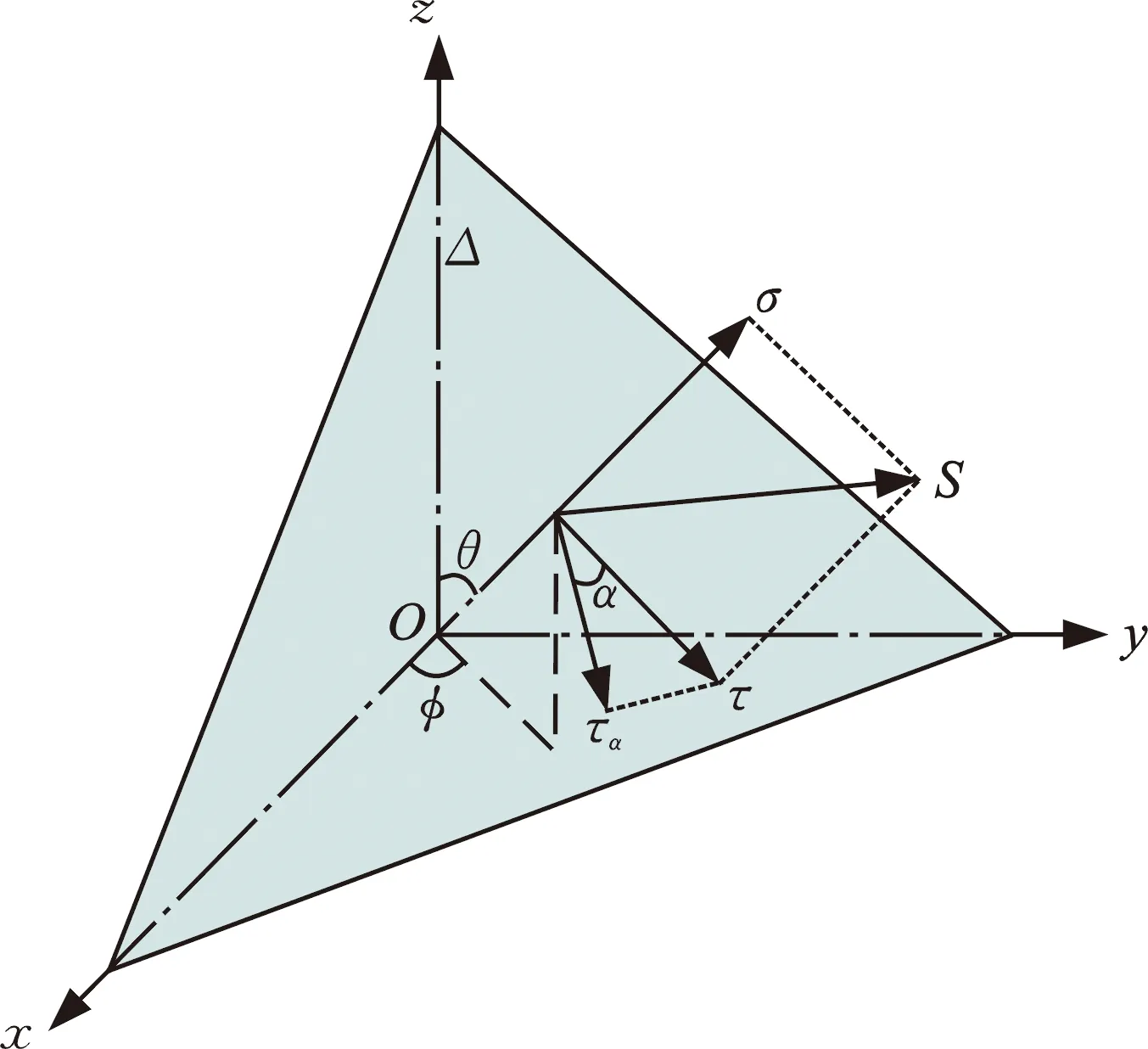
图8 物体内某点受力示意图Fig.8 Schematic diagram of a force on an object
不同疲劳准则对临界面的定义不同,上述7种临界平面高周疲劳准则所基于的临界面主要有:最大剪应力幅平面(McDiarmid准则,改进McDiarmid准则,Dang Van准则,Zhang-Yao准则);最大损伤的平面(Findley准则,改进Findley准则);第一主应力最大的平面(C-S准则)。
4.2.1最大剪应力幅平面
在随机载荷与比例载荷作用下,计算平面上剪应力幅值的方法不同。结构在承受多轴比例加载过程中,经过危险点O的任意平面时,正应力σ(t)与剪应力τ(t)仅大小发生变化,方向不会改变;而对于非比例载荷,正应力σ(t)方向仍然不会改变,仅大小发生变化,但剪应力τ(t)方向与大小均会随时间不断变化,其末端在平面上会形成一条轨迹线Ω,见图9a。
多轴非比例载荷计算等效剪应力幅值的方法主要有最长投影法、最长弦法、最小外接圆法、最小外接椭圆法和最大方差法。前4种方法需要计算出具体的轨迹线Ω才能使用,由于随机载荷非比例度较高,计算轨迹线Ω需要耗费大量时间,因此本文使用最大方差法计算等效剪应力幅。
最大方差法由SUSMEL[23]提出,以图8中的平面Δ为研究对象,将所有时刻剪应力τ(t)沿偏离基准向量α角度(0°≤α<180°)的单位向量q方向分解得到τq(t),见图9b。其中,单位向量q经推导为
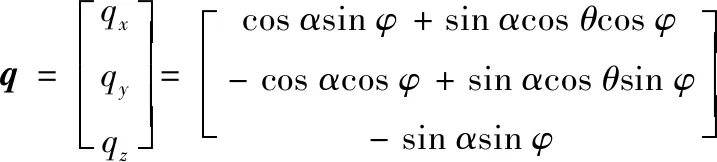
(15)
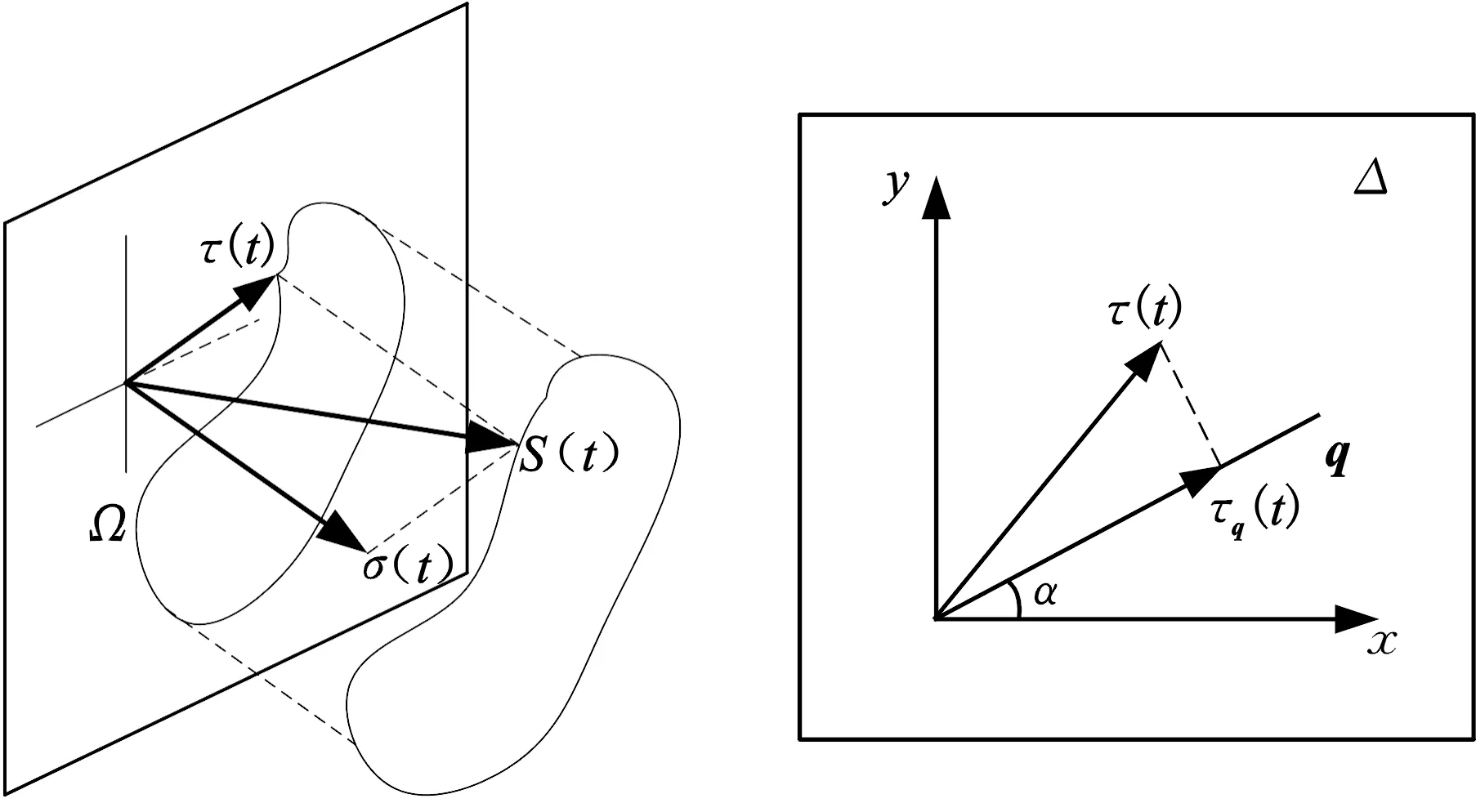
(a)临界面剪应力轨迹线 (b)临界面剪应力分解图图9 轨迹线与剪应力分解示意图Fig.9 Track line and schematic diagram of shear stress decomposition
所有时刻沿q方向分解的剪应力为
τq(t)=qTσij(t)lT
(16)
沿q方向分解的剪应力方差Var(τq(t))经过形式变换后可表示为
Var(τq(t))=dTCd
(17)
式中,d为方向余弦向量;C为协方差矩阵。
等效剪应力幅可表示为
(18)
其中,max(·)表示函数最大值。由式(18)可知,剪应力方差达到最大的平面即为最大剪应力幅平面。本次计算过程中θ、φ、α均以5°的增量增大,共进行46 656次计算,得到θ=125°、φ=95°且α=100°时,Var(τq(t))达到最大值35.24 MPa,则最大剪应力幅平面的法线方向可表示为
l1=(-0.071,0.816,-0.574)
(19)
提取最大剪应力幅平面上的正应力时间历程σ_1-t与剪应力时间历程τ_1-t绘制于图10。
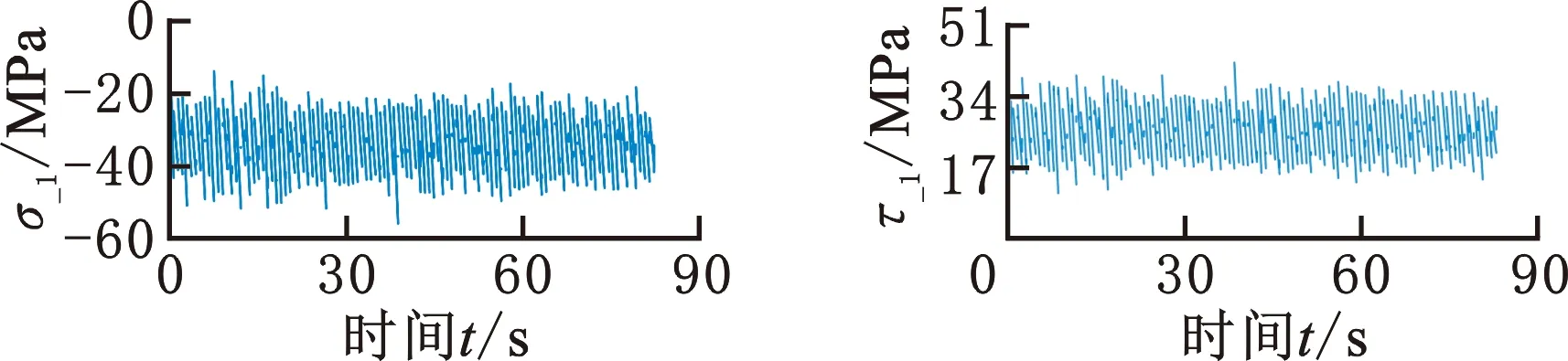
(a)正应力 (b)剪应力图10 最大剪应力幅平面正应力与剪应力时间历程Fig.10 Normal stress and shear stress time history of maximum shear stress amplitude plane
4.2.2最大损伤的平面
Findley准则提出将剪应力幅与最大正应力的组合达到最大值的平面定义为临界面,并在该平面上计算疲劳损伤。其中,剪应力幅可根据式(18)计算,而正应力仅大小变化,方向始终垂直于平面,因此可以使用常规方法计算幅值、均值等参数。在非比例载荷下,BOLCHOUN等[24]使用整个循环下的最大正应力值进行计算,且当应力比R=-1时有σn,max=σa;陈志超[25]利用Goodman公式对临界面的正应力幅值进行修正,将所得到的对称循环加载时的最大正应力幅作为最大正应力。本文在计算最大正应力时也采用上述方式进行求解,即先使用雨流计数法对平面上正应力时间历程进行幅值与均值的统计,再通过Goodman平均应力修正法将均值修正为0,从而得到对称循环加载时的最大正应力幅,Goodman平均应力修正法表达式为
(20)
其中,σa,-1为应力比为-1时的循环应力幅值。
计算过程中θ、φ、α均以5°的增量增大,共进行46 656次计算,得到θ=135°、φ=85°且α=95°时,τaeq+kσn,max达到最大值14.89 MPa,其中,正应力在疲劳损伤中所占的比重k可由式(8)计算得到。最大损伤平面的法线方向可表示为
l2=(0.062,0.704,-0.707)
(21)
提取最大损伤平面上的正应力时间历程σ_2-t与剪应力时间历程τ_2-t绘制于图11。
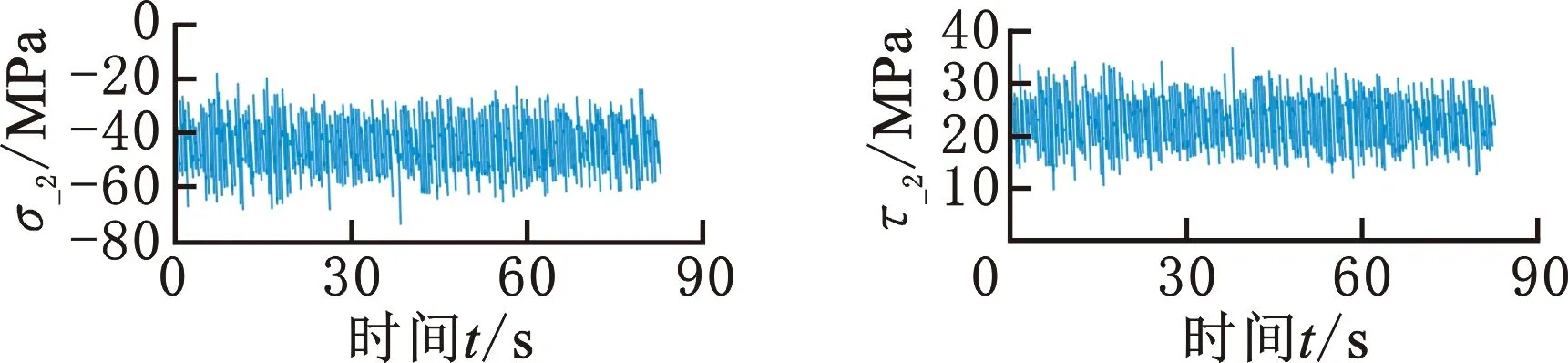
(a)正应力 (b)剪应力图11 最大损伤平面上正应力与剪应力时间历程Fig.11 Normal stress and shear stress time history of maximum damage plane
4.2.3第一主应力最大的平面
由于随机载荷下的主应力方向不断变化,文献[26]提出通过权函数计算平均主应力方向,文献[14]在此基础上简化了求解过程,提出平均主应力轴与对应第一主应力σ1达到最大值σ1max时刻的瞬时主方向重合,因此只需计算第一主应力达到最大值时刻对应的主平面。通过计算可得危险点第一主应力时间历程,见图12。提取第一主应力最大平面上的正应力时间历程σ_3-t与剪应力时间历程τ_3-t绘制于图13。

图12 危险点第一主应力时间历程Fig.12 First principal stress at the point of danger

(a)正应力 (b)剪应力图13 第一主应力最大平面上正应力与剪应力时间历程Fig.13 Normal stress and shear stress time history of the first principal stress maximum plane
由图12可以看出,当t=19.074 s时,第一主应力达到最大值94.314 MPa,此时θ=163.18°,φ=55.53°,则第一主应力最大值平面的法线方向可表示为
l3=(0.1638,0.2385,-0.9572)
(22)
4.3 多轴循环计数
循环计数是将复杂的载荷时间历程简化为具有循环概念的简单载荷,目前普遍认可的计数方法是雨流计数,但该方法通常用来处理单轴随机载荷与多轴比例载荷。对于多轴随机载荷,临界面上正应力与剪应力时间历程有相位差、峰谷值不同时出现等复杂情况,因此相比单轴载荷的处理更为复杂。
有关多轴载荷循环计数方法的研究报道已经有许多。JORDAN等[27]在实验中发现只有最大剪应变的一个半循环内的正应变变程对疲劳损伤是有效的,而另一个半循环内的正应变变程对疲劳损伤无贡献,即不必区分加载半循环和卸载半循环。WANG等[28]认为对疲劳裂纹扩展有贡献的有效正应变在两个相邻的最大切应变的转点之间。
本文根据文献[27]所提方法对临界面上正应力与剪应力时间历程进行雨流计数,举例说明计数过程,如图14所示。图14是一段剪应力与正应力时间历程曲线,以剪应力为主计数通道,提取到b-c-b′、f-g-f′、a-e-a′三个全循环。对于全循环b-c-b′,其变程为Δτ1,三个载荷信息点b、c、b′在正应力时间历程中的对应点分别为2、3、4′。根据文献[27]分别计算两个半循环2、3与3、4′的变程,并选取最大值Δσ1作为辅通道的计数结果,最终可得到第一个多轴计数结果为(Δτ1,Δσ1),同理可得到(Δτ2,Δσ2)、(Δτ3,Δσ3)。此外,使用这种方法对上述三种临界面下提取的剪应力和正应力时间历程分别进行多轴循环计数。

图14 多轴循环计数示意图Fig.14 Schematic diagram of multiaxis cycle count
5 多准则幅值分析及寿命预测
试验车辆转向节材料为QT400-15,抗拉强度σb=484 MPa,根据σ-1=0.4σbCDCSCLCR/Kf修正拉伸疲劳极限,通过查表[29]可得尺寸系数CD=0.89、表面质量系数CS=0.78、载荷系数CL=0.7、可靠性水平系数CR=0.753、疲劳缺口系数Kf=1.59,计算得到σ-1=44.55 MPa,对钢铁材料而言,超过107周次应力循环通常被认为无限寿命。为得到材料S-N曲线,还需要根据σ1000=0.9σbCR估算疲劳寿命为1000周次循环时对应的应力强度,得到σ1000=328.01 MPa。
材料的S-N曲线与T-N曲线通常用Basquin公式表示,其表达式分别为
(23)
(24)

根据以上参数,计算得到S-N曲线为
σa,cri=1703.5(2Nf)-0.2167
(25)
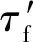
τa,cri=1081.8(2Nf)-0.2167
(26)
根据临界面上正应力与剪应力的多轴雨流计数结果可计算每种准则下的等效应力幅,并统计每种准则等效应力幅的分布情况。通过以上数据计算修正后的拉伸疲劳极限与扭转疲劳极限分别为σ-1=44.55 MPa,τ-1=28.29 MPa,其比值ξ=1.57。本次幅值统计分为小幅值[0,0.5σ-1(τ-1))、中等幅值[0.5σ-1(τ-1),0.8σ-1(τ-1))、大幅值[0.8σ-1(τ-1),∞)三个区间,具体如下:
小幅值
0≤σa,cri<22.28 MPa
0≤τa,cri<14.15 MPa
中等幅值
22.28 MPa≤σa,cri<35.64 MPa
14.15 MPa≤τa,cri<22.63 MPa
大幅值
σa,cri≥35.64 MPa
τa,cri≥22.63 MPa
记录每个区间载荷循环次数绘制于表3。本文8种准则均是针对转向节上同一节点的等效应力幅统计结果,统计得到的小幅值分布情况如下:McDiarmid准则占比最高达到78.4%,Zhang-Yao准则占比只有26.6%,Dang Van准则、Findley准则、改进Findley准则与改进McDiarmid准则占比接近。大幅值分布方面,Zhang-Yao准则占比最高达到59%,McDiarmid准则占比最小(仅为3.4%)。

表3 各准则等效应力幅分布统计Tab.3 Statistics on the distribution of the equivalent forces of each criterion
只有等效应力幅大于疲劳极限才会产生损伤,统计每种准则下有效的等效应力幅列于表4,并使用Miner线性损伤累积理论计算危险点的总损伤与寿命。Miner准则因形式简单、便于应用而被广泛使用,其表达式为
(27)
式中,D为累积损伤;ni为i级载荷的循环次数;Ni为i级载荷下达到寿命时的循环次数;j为载荷级数。
表4为计算得到危险点在每种准则下的累计损伤与寿命结果,使用Dang Van准则、Zhang-Yao准则计算寿命最为保守,其次是von Mises准则、改进的McDiarmid准则、Findley准则、改进的Findley准则、C-S准则,McDiarmid准则的预测寿命值最大,明显大于其他准则的预测寿命值。改进的McDiarmid准则与原准则相比,其预测寿命明显缩短,而改进的Findley准则预测寿命与原准则预测寿命接近。

表4 各准则下转向节损伤和寿命统计Tab.4 Statistics of the damage and life for the knuckle under each criterion
从计算成本方面考虑,每种准则的计算成本差异主要体现在提取临界面环节。von Mises准则不需要多轴循环计数与求解临界面,最便于应用;C-S准则使用第一主应力达到最大值时的应力分量便能计算临界面方向;最大剪应力幅平面需要计算所有平面的剪应力数据,挑选出等效剪应力幅最大的平面;最大损伤平面(Findley准则)计算成本最高,需要计算所有平面的剪应力与正应力数据,使提取的平面剪应力幅与最大正应力线性组合最大。
6 结论
(1)对转向节有限元模型进行了模态分析与验证,对比前6阶固有频率的相对误差均在10%以内,验证了模型满足仿真分析精度要求。将实车实测石块路乙等试验场强化路载荷谱作为疲劳分析的原始数据,并进行了转向节连接点载荷谱分解。
(2)分析了随机载荷下最大剪应力幅平面、最大损伤平面和第一主应力最大值平面三种类型临界面的选取方法,并提取了临界面上正应力和剪应力时间历程;通过多轴循环计数,获取到所有正应力幅与相对应的剪应力幅,并将多轴疲劳准则应用到随机载荷下的寿命预测。
(3)从等效应力幅分布、寿命预测结果和计算成本等方面对各准则进行了分析评估。研究结果表明,Zhang-Yao准则的等效应力幅整体偏大,其预测寿命与Dang Van准则的预测寿命接近,但明显短于其他准则的预测寿命,McDiarmid准则的大应力幅仅占3.4%,其预测寿命明显长于其他准则的预测寿命,而改进的McDiarmid准则预测寿命明显缩短,改进的Findley准则预测寿命与原准则预测寿命接近。von Mises准则计算成本低,最便于应用;Findley准则提取临界面过程最复杂,计算成本最高。

