考虑水化热影响的混凝土坝位移监测统计分析模型及其解析
华倩宇,苏怀智,杨立夫
(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.河海大学水利水电学院,江苏 南京 210098)
混凝土坝在施工期浇筑混凝土后,水泥水化过程释放大量水化热,将严重威胁结构的运行安全和结构寿命,尤其是对厚度较大的混凝土结构,如混凝土坝、闸墩、桥墩等易因温度应力产生表面裂缝或深层贯穿裂缝,以及因大量水化热消散产生额外变形[1]。在自然散热条件下,混凝土坝等大体积混凝土结构的内部水化热一般需要200 a左右才能完全消散[2]。混凝土坝的温度应力问题一直受到关注,为了减少水化热对工程的影响,国内外工程多采取通水冷却[3-4]、降低水泥含量[5-6]等措施降低混凝土坝内部残余水化热热量,但残余水化热仍是一个较普遍的现象。为保障混凝土坝的安全运行,通过对混凝土坝日常水位、坝体内部温度、位移等数据的实时监测,实现混凝土坝运行状况的安全评估[7]和变形预测[8]。根据吴中如[9]院士提出的大坝位移统计模型,可以进一步量化水位和温度对大坝位移的影响程度,但如何通过监测资料量化残余水化热对混凝土坝位移的影响程度仍是一个亟待解决的问题。
随着对混凝土坝安全监测的日益重视,监测仪器布置的时间越来越早,在这些监测数据的初期,不可避免地包含了残余水化热消散过程的影响[10-11],但现有统计模型无法直接分离出残余水化热对混凝土坝位移的影响。薛素铎等[12]基于水泥水化反应三阶段的特征提出S形水化热模型,朱伯芳院士提出混凝土绝热温升的新计算模型[13],这些模型通过结合有限元模型进行数值模拟,其结果能与试验数据较好地吻合,但这些模型是针对实验室中的混凝土标准试块建立,由于混凝土体积差异以及边界影响因素差异,这些模型不能直接用于量化混凝土坝的水化热。针对这一点,刘丹丹等[14]建立了施工期混凝土温度统计模型,黄耀英等[15]建立了小尺度施工期温度统计模型,这些模型都能分离在通水冷却影响下水化热分量,但不能直接用于混凝土坝坝内残余水化热消散阶段。
现已有很多成熟的算法用于建立混凝土坝的位移统计模型,如徐洪钟等[16]引入偏最小二乘法对混凝土坝的位移统计模型进行求解,Xu等[17]提出基于遗传算法的偏最小二乘法建立混凝土坝的位移统计模型,有效避免了回归因子间多重共线性对回归模型的影响。本文在偏最小二乘法的基础上,提出向后删除变量-偏最小二乘法,基于这一改进算法建立混凝土坝位移统计模型;针对监测资料中包含水化热影响的这类工况,利用一维热传导方程的近似解推导出水化热分量的表达式;借助非线性最小二乘法对包含非线性项的水化热分量进行回归分析,提出了完整的混凝土坝水化热位移分量分离流程;通过对混凝土坝实际监测资料的分析,首次实现了混凝土坝残余水化热对实际位移影响的量化分析。
1 基于改进偏最小二乘法的混凝土坝位移统计模型建立
1.1 混凝土坝位移统计模型
混凝土坝在水压力、扬压力、泥沙压力和温度等荷载作用下,坝体任一点将产生相应的位移矢量δ,根据成因将其分解为水压分量、温度分量和时效分量[9],即
δ′=δH+δT+δθ
(1)
式中:δ′为混凝土坝某点顺河向位移;δH为水压分量;δT为温度分量;δθ为时效分量。
水压分量如下式所示:
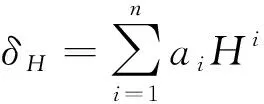
(2)
式中:ɑi为系数因子;H为上游水深;n为指数因子,重力坝取3,拱坝取4。
当只有气温监测资料时,可选用多周期的谐波作为因子,即温度分量如下式所示:
(3)
式中:b1i、b2i均为系数因子,i=1表示年周期,i=2表示半年周期;一般m2取1或2。
当温度计个数较多时,用各温度计的测值作为因子,使回归方程中包含的因子过多,从而增加观测数据处理的工作量。为解决这一问题,本文采用相同高程温度计测值的等效温度作为因子[18],此时温度分量如下式所示:
(4)
(5)
(6)
式中:b1i、b2i为系数因子;¯Ti为各层温度计测值等效温度的平均温度;βi为各层温度计测值等效温度的梯度;Ati为相同高程温度分布的面积;Mti为Ati对相同高程温度分布纵轴的面积矩;Bi为对应高程坝体截面宽度;m为不同高程温度计分布总层数。
时效分量如下式所示:
(7)
式中:c1、c2为系数。
1.2 偏最小二乘法的改进
偏最小二乘法是一种先进的多元统计分析方法,能有效解决变量间多重相关性的问题,故适用于影响因素较多的大坝位移统计模型[19-20]。从其算法特点和实际应用来看,传统的偏最小二乘法也存在不足之处,如其提取的主成分可能只对自变量有很强的综合能力,而与因变量的相关程度并非最大;对含有较多自变量的模型拟合效果欠佳,且不能对自变量进行筛选和识别。故传统的偏最小二乘法无法剔除与因变量不相关的信息,本文针对这一点进行改进,即将解释性不强的自变量剔除,使回归方程更加简洁、精确。
由第1.1节可知混凝土坝位移的影响因素较多,因此混凝土坝位移回归方程包含的回归因子较多,其中可能包含对混凝土坝位移影响不显著的因子。如果回归方程存在这类因子,将会扩大估计方差,降低模型精度,影响回归方程的稳定性,此时需要将不显著的回归因子从混凝土坝位移模型中剔除[21]。判断某个回归因子是否有必要从混凝土坝位移统计模型中删除,关键是看这个回归因子能否对混凝土坝位移提供显著的附加信息。考虑采用t检验[22]考察每一个回归因子对混凝土坝位移的影响程度。为尽可能多地保留回归因子,用向后删除变量法剔除多余因子。其具体步骤如下:
步骤1将所有的回归因子(p个)包含在混凝土坝位移线性回归模型中,依次对每一个回归因子进行t检验;
步骤2如果有若干回归因子未能通过t检验,剔除t的绝对值最小的回归因子;
步骤3将剩余的p-1个回归因子拟合混凝土坝位移线性回归模型,重新对p-1个剩余回归因子进行t检验,剔除t的绝对值最小的回归因子;
步骤4重复步骤3,直到混凝土坝位移回归模型中剩余的所有回归因子均通过t检验。
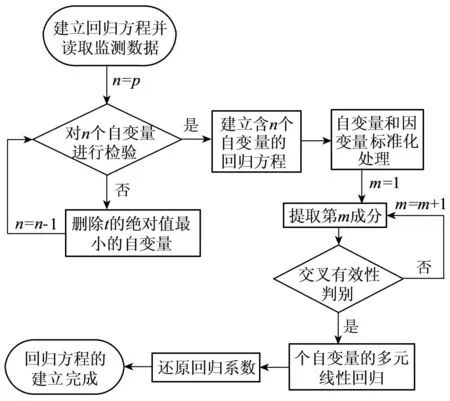
结合上述对偏最小二乘法的改进,基于改进偏最小二乘法的混凝土坝位移统计模型构建流程具体步骤如下:读取混凝土坝位移、水位和温度的监测资料,根据1.1节将混凝土坝的水位、温度和时效因作为自变量集合X′,混凝土坝监测位移作为因变量集合Y,建立二者之间的线性回归方程,通过向后删除变量法对自变量集合X′中的每一个自变量进行多重共线性分析并将不显著的自变量删除,剩下来的自变量组成新的自变量集合X。接下来分别在自变量集合X和因变量集合Y中提取s1和u1两个主成分,对主成分的要求是最大程度地携带原数据系统中的变异信息,同时相关程度也要达到最大,使二者之间的协方差取最大值,即有:
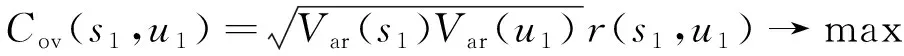
(8)
式中:Cov(s1,u1)为s1和u1的协方差;Var(s1)、Var(u1)分别为s1和u1的方差;r(s1,u1)为s1和u1相关系数。
提取第一主成分s1和u1后,分别进行X对s1的回归和Y对u1的回归,出现两种情况:第一种是回归方程已经达到满意的精度,那么就可以停止计算;第二种是未达到满意的精度,那么就需要利用X被s1解释后的残余信息和Y被u1解释后的残余信息,然后进行第二轮主成分的提取,得到第二主成分s2和u2。如此反复,直到能达到一个较为满意的精度为止。若最终对X提取了m个主成分,记为s1,s2,…,sm,则Y对X的回归分析即转化为Y对s1,s2,…,sm的多元线性回归分析,而主成分s1,s2,…,sm均可由X线性表示,所以最后可以还原成Y对X的回归方程。

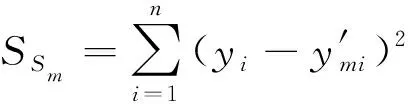
(9)
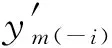
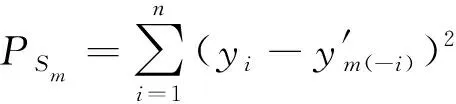
(10)
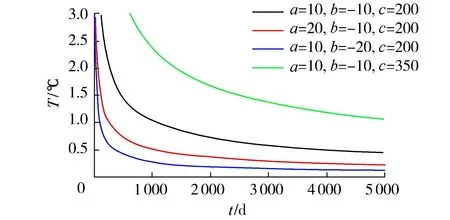
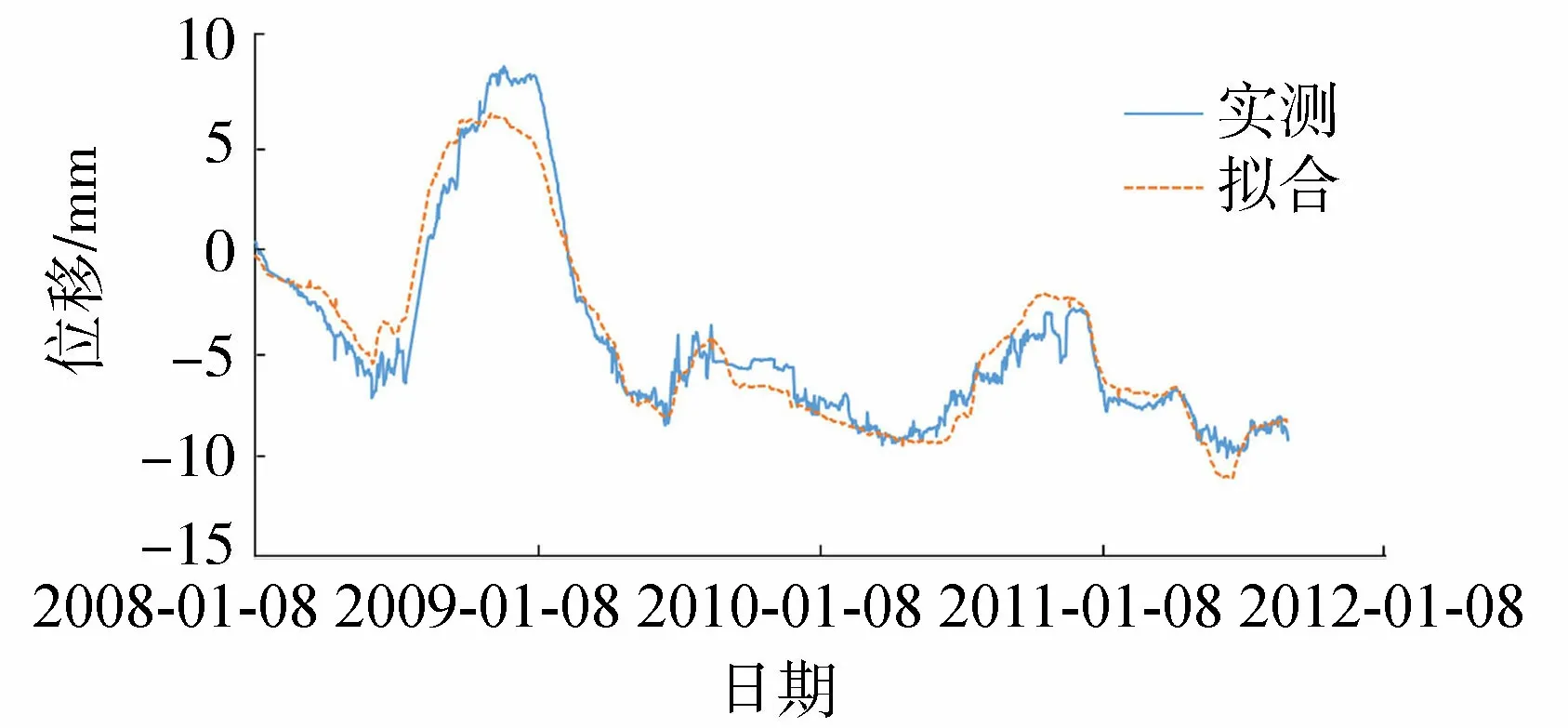
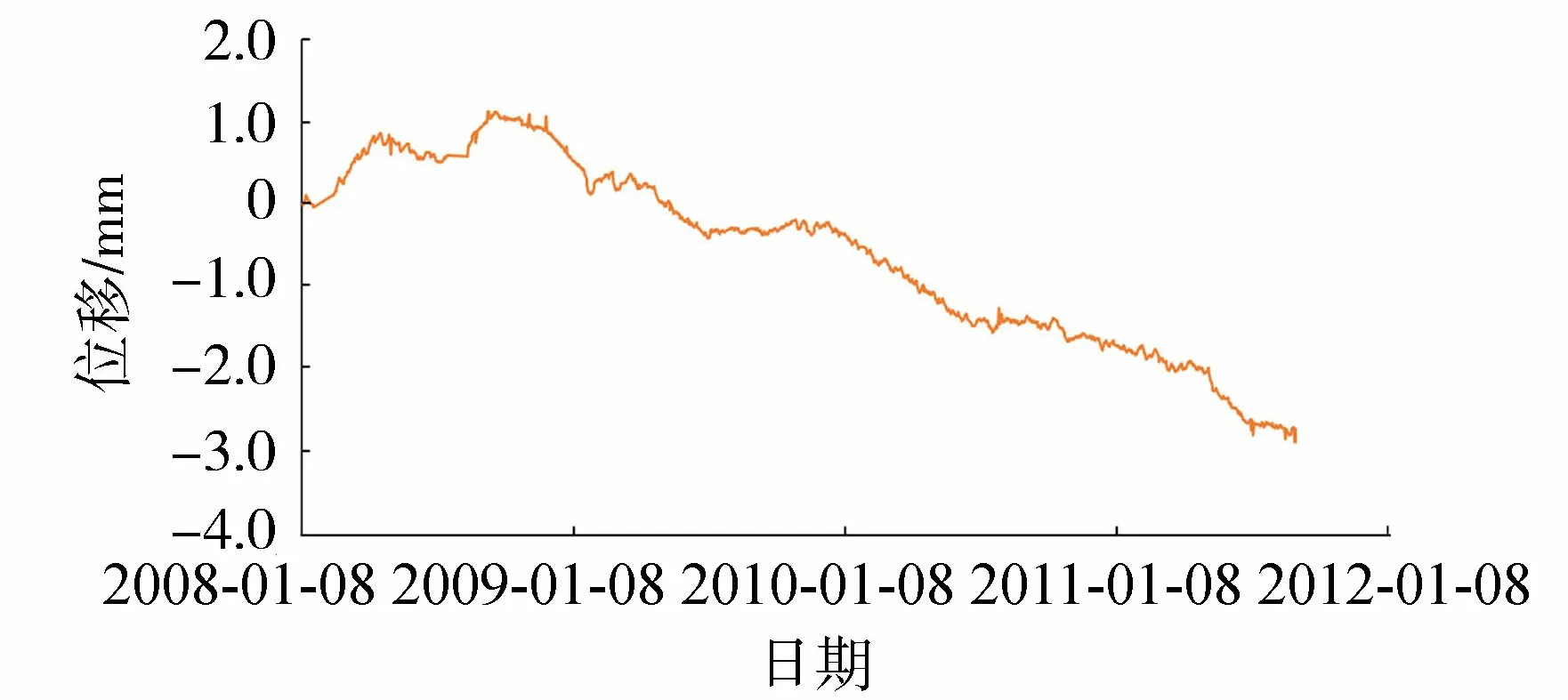
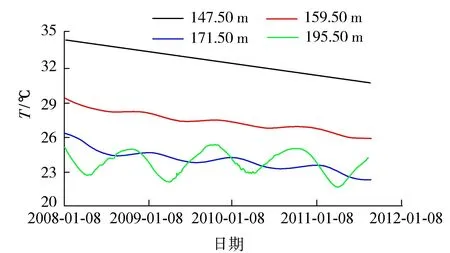
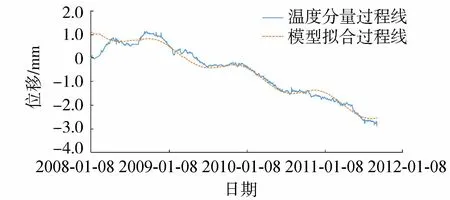
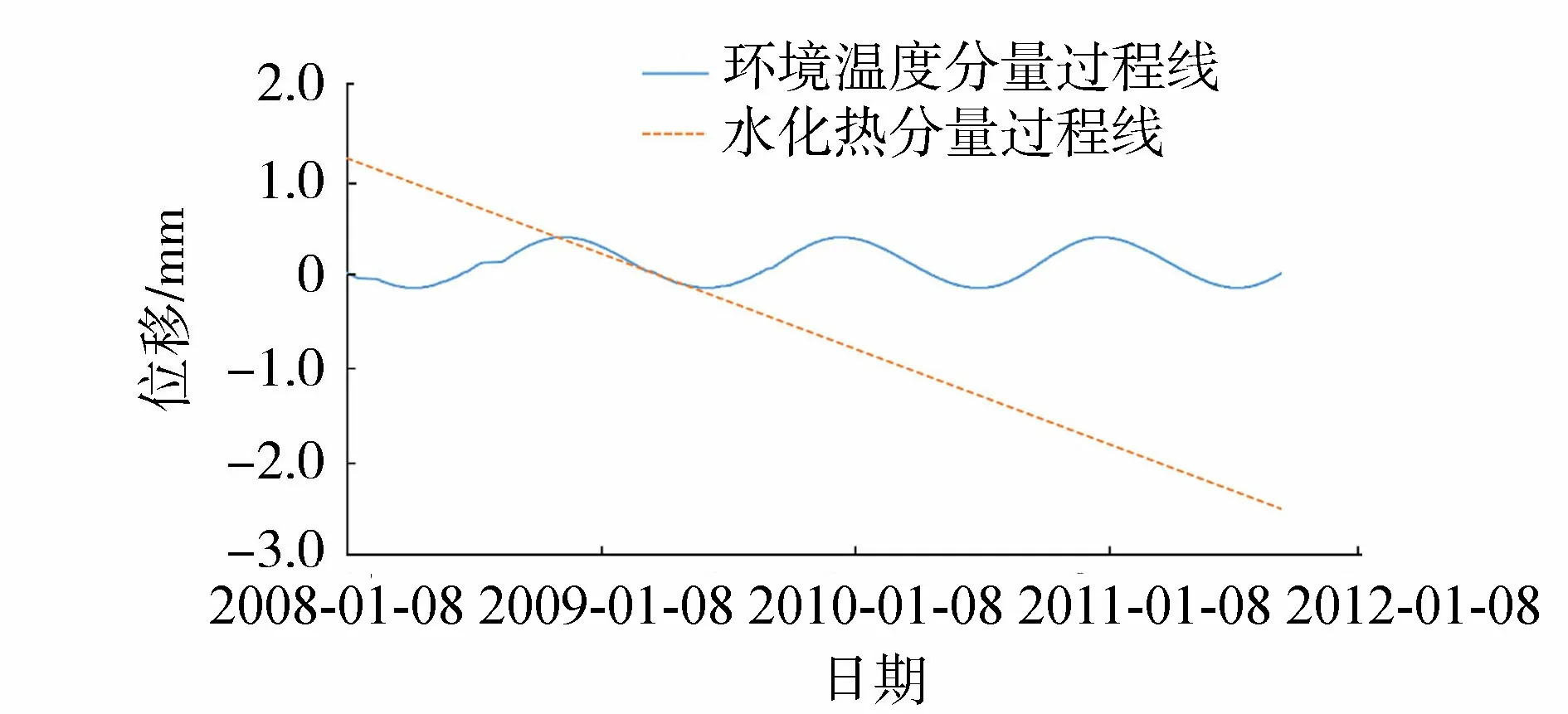
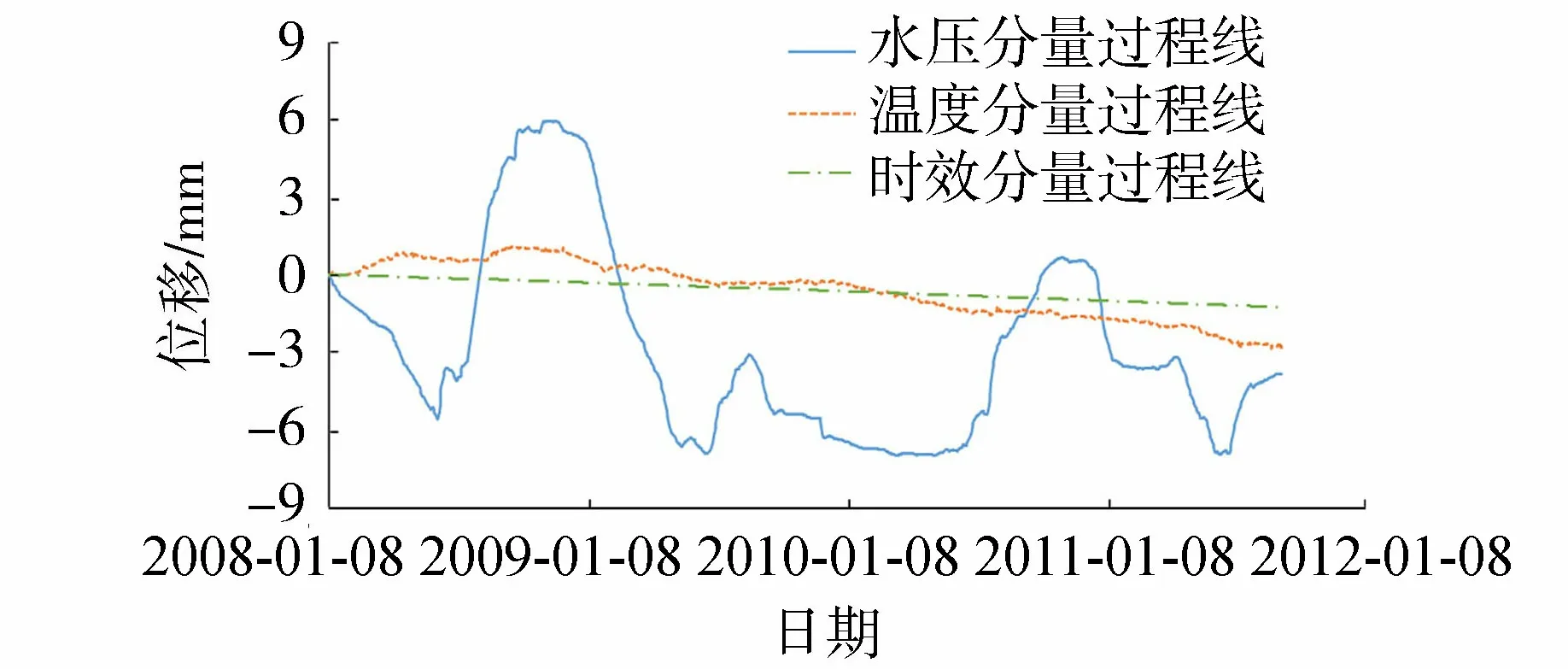
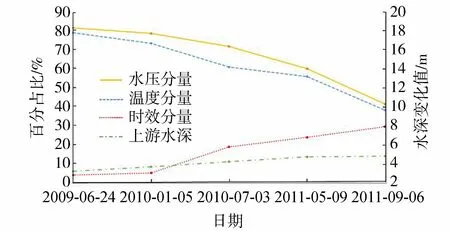
如果回归方程的误差较大,则PSm对样本点的变动就很敏感,其数值会增大。因此,当PSm达到最小值时,此时对应的m即为所求的成分个数。通常,总有PSm>SSm,而SSm (11) 因此,对大坝安全监测的因变量Y,采用下式判断成分sm的交叉有效性: (12) 在偏最小二乘法建模的每一步计算结束前可进行交叉有效性检验,如果在第m步提取的sm成分的边际贡献显著,则进行第m+1步提取成分的计算。 改进偏最小二乘法利用不显著回归因子的筛选以提高所建模型的精度。同时将多元线性回归分析、主成分分析和典型相关分析进行有机结合,吸取主成分回归分析中从解释变量提取信息的思想,注意了主成分回归中所忽略的自变量对因变量的解释问题,该方法能有效解决变量间的多重相关性问题。综合第1.2节内容可得基于改进偏最小二乘法的混凝土坝位移统计模型构建流程如图1所示,该算法针对混凝土坝的监测资料所构建的自变量集合X和因变量集合Y,先进行多重共线性检验并使用向后删除变量法,剔除对大坝位移影响不显著的回归因子,然后再对剩下的回归因子使用偏最小二乘法,最后建立混凝土坝位移的统计模型。这一算法可有效剔除多余自变量,且不受剩余自变量间多重线性相关的影响,建立合理的混凝土坝位移统计模型。 图1 基于改进偏最小二乘法的混凝土坝位移统计模型构建流程 通过观察多个大坝运行期前几年的温度计实测数据,发现温度时程曲线存在环境温度引起的周期性波动外,还呈现平缓的下降趋势,这一现象在混凝土厚度较大的坝基附近尤为明显。经分析,这是由于混凝土坝浇筑期间水化热未完全消散而残留在坝体内,在蓄水后由于上下游环境温度和坝体内部温度的差异而进一步逐渐消散,直至坝体内部温度与外界环境温度达到一个相对平衡的状态。为了研究这一部分水化热对大坝变形的影响,需要将其与其他影响因素分离。 由于大坝沿坝轴线方向和竖直方向尺寸较大,且热交换主要发生在上下游坝面,即热传递方向为顺河流方向,故混凝土坝体内部水化热消散的问题即是一个内部没有热源的一维热传导问题: (13) 式中:T为垂直于坝轴线方向坐标为x处的温度;α2为导温系数。 对于同一座大坝,其上下游表面温度近似相等,且越靠近坝体横截面中心坝体内部温度越高,不妨设其为一个关于坐标x开口向下的抛物线方程φ(x),故初始条件为 式中:L为不同高程坝体截面宽度;b、c为待定参数,其中b<0。 考虑到混凝土坝的体积较大,将初始温度分布函数φ(x)延拓至无限区间后可把该问题视作热传导方程Cauchy问题,此时热传导方程的理论解为 (15) 由此可得混凝土坝上同一高程的平均温度为 (16) 式(16)中含有广义积分,无法求解该积分具体数值。通过选取多组参数α、b、c,并在同一组参数条件下,将无穷积分区间取为多组有限区间进行积分计算,并利用MATLAB绘出相应的温度时程曲线。选取其中4组不同α、b、c值在区间[0,L]绘出理论解的温度时程曲线如图2所示。 图2 不同参数组合时理论解的温度时程曲线 (17) 式中:b1代表最高水化热的影响;b2代表热扩散系数的影响且b2>0;b3代表混凝土龄期的影响且b3>0。 同样,选取多组不同的b1、b2、b3求取近似解,其中4组近似解的温度时程曲线如图3所示。 由图2和图3可知,改变理论解与拟合解的参数都能保证二者温度时程曲线凹凸性与整体趋势的相似性,故提出的近似解式(17)是合理的。 由于混凝土大坝任一点位移与各点变温值呈线性关系[6],故温度分量中的水化热分量δTW可直接使用与式(17)相差一个系数k的等式表示,即 (18) 混凝土坝内部的温度场一部分是由坝体的外部环境温度影响,但运行不久的混凝土坝的坝内还残留一部分水化热,该部分的水化热在一定程度上也会影响混凝土坝的坝体内部温度场。因此在利用混凝土坝坝体的温度实测数据建立混凝土坝温度位移分析模型时可将其进一步分解为式(4)所示的环境温度分量和式(18)所示的水化热分量来表示,即 (19) 式中:δTE为位移的环境温度分量;δTW为位移的水化热分量。 根据以上原理和方法,结合某混凝土重力坝的位移、水位、坝体温度等实测资料,利用改进的偏最小二乘法构建该坝顺河流方向的位移统计模型,并对位移温度分量予以分离,在此基础上,利用该温度位移建立分析模型,以量化坝体内部残余水化热对混凝土坝位移的影响程度。 某水利枢纽工程主坝为全断面碾压混凝土重力坝,最大坝高130 m,坝顶长720 m,共分为27个坝段。选取该混凝土坝的6A号非溢流坝段,对其2008年1月8日至2011年9月6日之间200 m高程的水平位移、坝体温度和水位监测数据进行分析,图4为坝上游水深顺河向位移过程线。 图4 坝上水深和6A号坝段水平位移过程线 由于该工程为混凝土重力坝,故式(2)中的指数因子n选为3;根据选取坝段温度计分布图及监测数据,式(4)中的层数m取为10。为使回归方程常数项较小,设定初始监测日期为回归方程初始状态。最终建立如式(20)所示的统计模型,模型中共含有25个回归因子。 (20) 式中:H0为初始监测日对应的上游水深;T0i为初始监测日所对应的各层温度计测值等效温度的平均温度;β0i为初始监测日对应的各层温度计测值等效温度的梯度;t0为初始监测日,取值为1。 各因子均转换为相对量,故下文所涉及的混凝土坝位移的不同分量均为相对于初始监测日的相对位移。 偏最小二乘法提取了4个主成分来表征剩下的17个回归因子,交叉的有效性为0.091 951,并且对位移进行了回归统计。回归模型的精度可用位移解释能力检验,各个回归因子的系数如表1所示。该回归模型对因变量即位移的解释能力为0.938 3,表明该回归模型合理且精度较高。同样可以通过图5中实测位移的过程线和统计模型拟合出的过程线看出该统计模型拟合精度较高。 图5 高程200 m处实测与拟合位移过程 表1 剩余17个回归因子系数 此外,从位移统计模型中,将温度分量分离出来,得到位移的温度荷载分量δT并在图6中绘制其过程线。从图中可以看出,位移的温度荷载分量呈现一定波动变化的同时,整体呈现负向增大趋势。 图6 位移的温度荷载分量过程 这一现象表明坝内温度受环境温度影响呈周期性波动,导致位移的温度荷载分量呈周期性波动。与此同时,当水化热逐渐消散时,坝内温度逐渐下降,顺河向位移逐渐减少,即位移的温度荷载分量出现负向增大。简而言之,位移的温度荷载分量除了受呈周期变化的环境温度影响以外,还受到未消散的水化热影响。 首先选取高程分别为147.50 m、159.50 m、171.50 m和195.50 m的温度计数据,将这4个不同高程的温度数据分别进行等效温度处理后作出其等效温度过程线如图7所示。 图7 典型高程等效温度过程线 由图7可知:不同高程的坝内温度除周期性波动以外,均有一定程度的下降,说明坝内留有未消散的水化热;越接近坝基,温度下降趋势越明显,说明残留的水化热更多;越接近坝基,温度的周期性波动幅度越小,说明受环境温度的影响更小。 对图6和图7分析可知,水化热分量对位移有一定的影响。为进一步分析其影响程度,需将其从温度荷载分量中分离出来。 根据第3节建立如下统计模型: (21) 计算可得各个因子的系数如表2所示。该回归方程的确定系数为0.961 1,表明模型合理且拟合精度较高。图8为从混凝土坝位移统计模型中分离出的温度分量过程线和利用温度位移统计模型拟合出的过程线,从该图中亦可以看出温度位移统计模型拟合效果较好。 表2 最终7个回归因子系数 图8 温度分量实际过程线与拟合过程线 由图8可知,开始监测的前3个月坝内温度场还未稳定,此时坝体内的水化热还没有开始消散,该模型拟合效果稍差。当坝内温度场基本稳定,即水化热开始消散时,拟合精度较高,总体效果良好,说明上面分离出的温度分量表达式与环境温度分量表达式是合理的。利用该温度位移模型分离出大坝位移的环境温度分量和水化热分量,绘制的位移过程线如图9所示。 图9 位移的水化热分量和环境温度分量过程 通过实例计算得知混凝土坝的位移影响因素中的确存在水化热分量,且通过温度位移统计将其从混凝土坝监测位移中成功分离,但其对大坝整体位移影响程度的大小,以及是否值得重视,还需要进一步分析。首先利用混凝土坝位移统计模型将监测位移的水压力分量、温度分量以及时效分量分离出来并绘制这三个分量的位移过程线在图10中。 图10 位移的水压分量、温度分量和时效分量过程 由图10可知,水压分量为混凝土坝位移的主要影响因素;随着时间推移,时效分量逐渐增大但增长趋势逐渐平稳;随着时间推移,温度分量明显增大且增长趋势逐渐变大。为凸显温度分量在混凝土坝总位移中的占比,通过观察混凝土坝实测位移过程线中与2011年9月6日监测位移数值相近的点,最终选取2009年6月24日、2010年1月5日、2010年7月3日、2011年5月9和2011年9月6日分别计算混凝土坝位移的水压分量、温度分量和时效分量占当日监测位移的占比,最后将各分量这5天的占比以及相对于初始监测日的上游水深变化值绘制在图11中。 图11 位移的各分量占比及上游水深 由图11可知:随着上游水深相对于初始监测日由17.8 m减少至9.6 m,大坝位移的水压分量占比随之由81.8%减小至41.3%。随着时间的推移,大坝位移的时效分量和温度分量占比均呈上升趋势,但时效分量的占比较小,仅由5.5%增大至13.4%,而温度分量由3.5%增大至29.3%。由此可见水压和温度是影响大坝总位移的主要因素。 从图9可以看出温度分量中的环境温度分量呈小范围的周期性变化,而水化热分量呈大幅度负向增长的趋势,故导致温度分量占比明显增大的原因是水化热分量的明显增长。为直观地展现水化热分量对大坝位移的影响程度,同图11中选取2009年6月24日、2010年1月5日、2010年7月3日、2011年5月9和2011年9月6日分别计算水化热分量的拟合值及其占当日监测位移的百分比,最后将结果绘制在图12中。从图12中可知,刚开始监测时,大坝位移的水化热分量在大坝总位移中的占比仅为3.1%,随着时间的推移,水化热分量的占比发生明显增大,达到了27.3%。 综合图11和图12可知,大坝开始变形监测后,朝向下游方向的大坝位移由于各种原因逐渐减小并出现朝向上游的位移,起初仅有一小部分是残留在坝体内逐渐消散的水化热导致的,往往容易被忽视,但随着时间的推移,这部分水化热对大坝位移的影响逐渐凸显出来。因此残余水化热对大坝位移的影响是不可忽视的,在对同类工程进行大坝变形监测及风险评估时应当对这一部分位移予以足够的重视。 a.向后删除变量-偏最小二乘法可剔除回归模型中对因变量影响不显著的回归因子,有效避免剩余回归因子间的多重相关性对回归模型的影响,从大坝位移回归模型中合理、有效地分离出温度分量。 b.基于一维热传导方程的理论解,得到受水化热影响的坝体温度的简化表达式,进而利用混凝土坝温度变形与温度呈线性关系推导出位移的水化热分量的表达式。该表达式形式简单,更适合作为影响因子用于建立混凝土坝位移统计模型。 c.工程实例分析表明,利用改进的偏最小二乘法所建立统计模型,拟合精度高,同时能够以较高的精度分离出混凝土坝监测位移中的水化热分量。通过计算出混凝土坝位移水化热分量占监测位移的百分比,表明起初残留水化热对大坝位移的影响并不明显,容易被忽视,但随着时间的推移这一影响逐渐凸显,成为影响大坝位移的重要影响因素之一。残余水化热对大坝总位移的影响应当予以重视。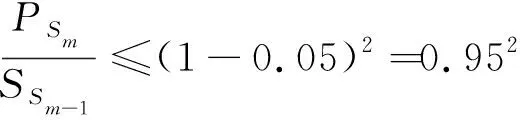
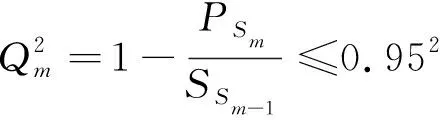
1.3 基于改进偏最小二乘法的混凝土坝位移统计模型构建流程和步骤
2 基于热传导方程的混凝土坝水化热位移理论推导
2.1 热传导方程
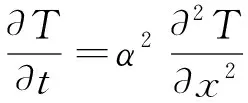
2.2 水化热分量推导
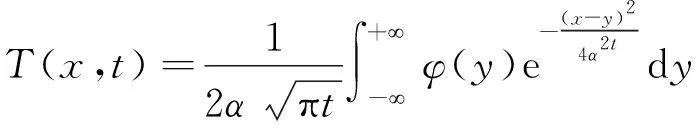
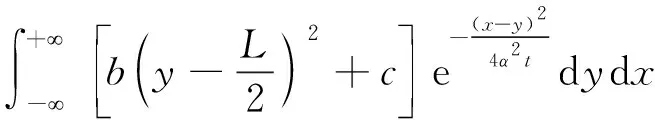
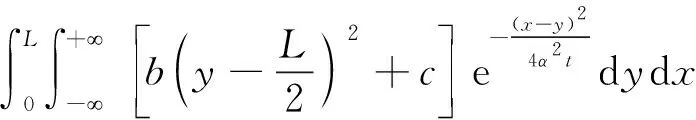
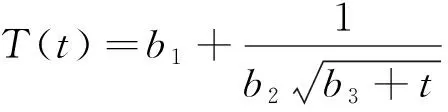
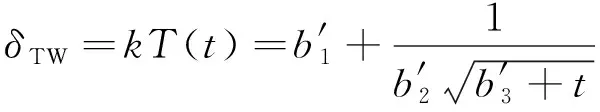
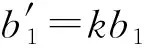
3 考虑水化热影响的混凝土坝温度位移分析模型
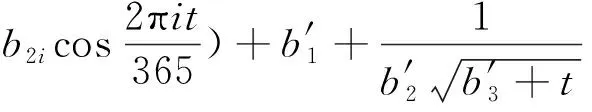
4 实际工程案例分析
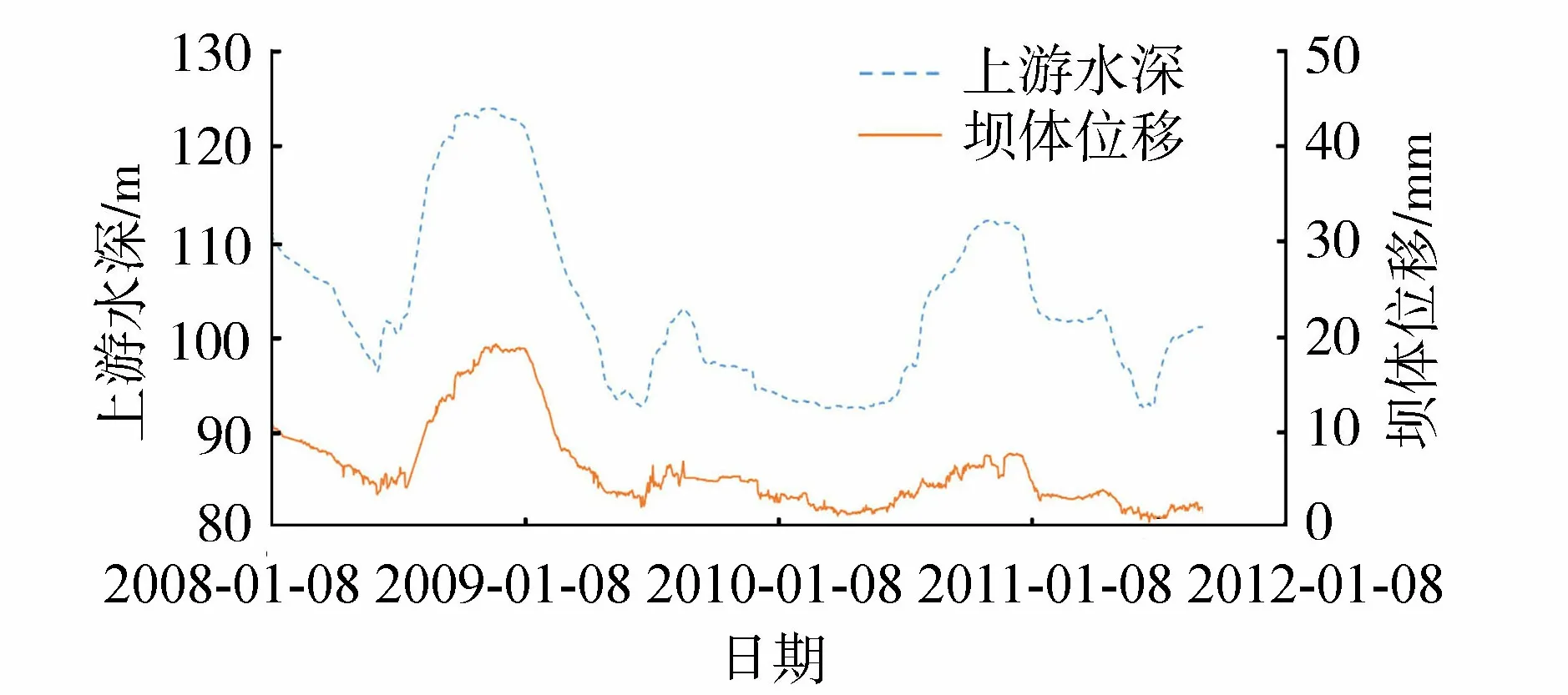
4.1 工程及监测概况
4.2 位移统计模型及其分析
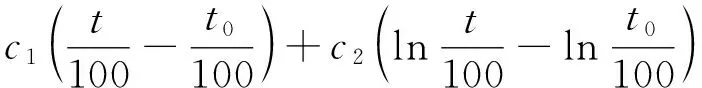
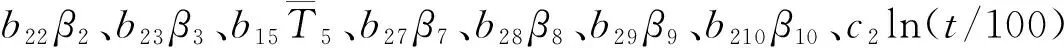

4.3 混凝土坝温度位移统计模型及其水化热影响分析

5 结 语

