桩周饱和黏土非齐次渗流固结解

高子坤, 傅长荣

(1.丽水学院土木工程系，浙江 丽水 323000; 2.浙西南地质灾害防治研究所，浙江 丽水 323000)

超静孔隙水压力的消散速度及程度影响基础的承载力，并反映饱和土层固结度及压缩量随时间的变化规律。该问题相关的研究主要包括初始超静孔隙水压力的确定，反映超静孔隙水压力时空变化规律理论或数值解答的推导[1-2]及其在工程与环境问题解决中的应用等内容。

Sagaseta[3-4]探讨了不排水条件下桩-土作用引起的地基土位移、应力求解等问题；高子坤等[1,5-6]对半空间中压桩挤土造成的附加位移、应力、超静孔隙水压力及其消散过程展开研究，得到相应问题的解答，但针对土体超静孔隙水压力消散固结问题的解答局限于齐次边界；陈文[7]分析了饱和黏土中沉桩挤土机理及效应；刘时鹏等[8]采用K0固结排水模型，推导了饱和黏土中压桩挤土问题的应力场并得到初始超静孔隙水压力解答；曹权等[9]针对饱和软黏土中压桩挤土问题，引入对数应变参数描述大变形及软化等特征，推导土中孔扩张造成的应力场，并分析了超静孔隙水压力分布规律；姚笑青等[10-11]对沉桩在饱和黏土中引起的超静孔隙水压力进行了估算。

本文针对空间轴对称非齐次固结问题，建立非齐次固结定解条件并推导解答，计算得到超静孔隙水压力随时间、空间变化的模拟数据，绘制时间-平均固结度曲线、水头等值线和流速矢量图。结合工程实例，应用实测的桩基承载力随时间变化数据换算平均固结度，以验证理论推导的正确性。

1 解答推导

空间轴对称问题固结微分方程为[12]

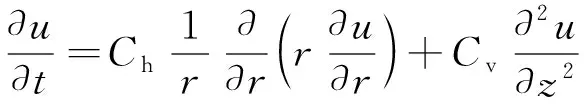
(1)

式中：u为超静孔隙水压力；Ch、Cv分别为水平和竖直方向的固结系数；z、r分别为竖直和水平(径)向坐标。

建立固结模型如图1所示，包括桩端平面(地下或地表)、桩尖平面、桩土接触界面以及初始超静孔隙水压力影响范围等。

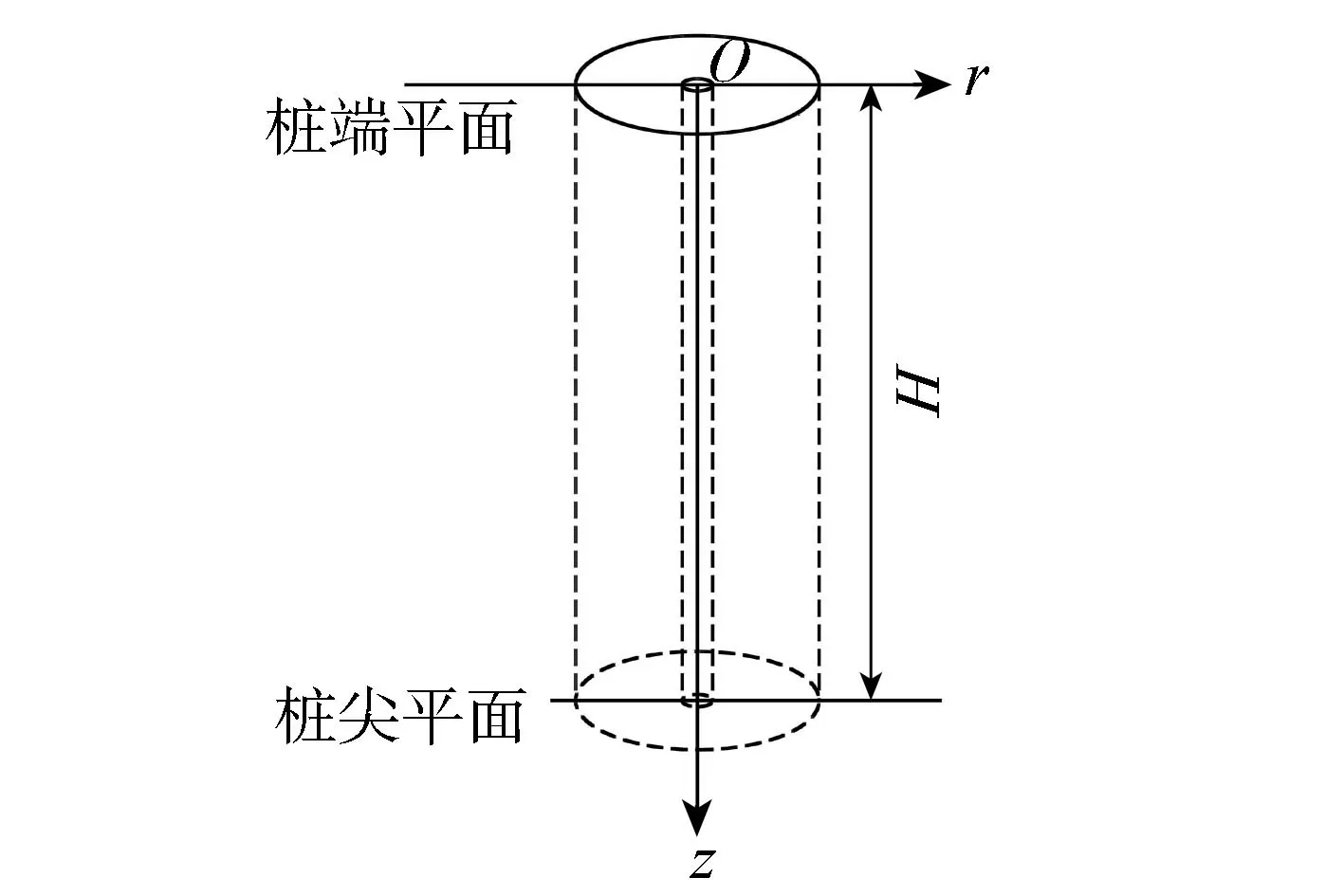
图1 固结模型

考虑固结开始时，场地附近的河流或水库水位影响，建立桩端平面水头边界；考虑基桩以承压含水砂砾石为持力层，或为加速固结排水设计砂井抽水降压等措施的影响，建立桩尖平面水力梯度边界，即式(1)的边界条件为

(2)

初始条件为

u|t=0=f(r,z)

(3)

式中：φ(t)、ψ(t)分别为桩端边界处水头压力函数和桩尖平面边界处水力梯度函数；f(r,z)为任意函数；rw为桩孔半径；re为f(r,z)影响半径；H为桩长。

对定解方程式(1)进行齐次化运算，令：

u(r,z,t)=V(r,z,t)+W(z,t)

(4)

其中W(z,t)=zψ(t)+φ(t)

依据式(2)及W(z,t)表达式可得桩尖平面水力梯度Wz(H,t)=∂W(H,t)/∂z=ψ(t)，桩端平面水头W(0,t)=φ(t)。

将式(4)代入式(1)可得：

(5)

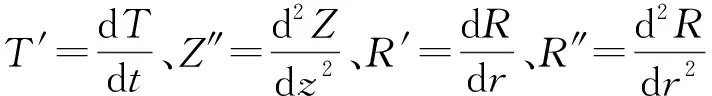
RZT′-ChDZT-CvTRZ″=0

(6)

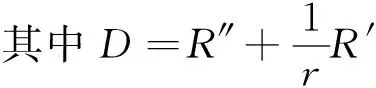
引入参数μ、λ，对式(6)分离变量可得：

(7)

式(7)满足边界条件R′|r=rw=0，R|r=re=0、Z|z=0=0、Z′|z=H=0和初始条件V|t=0=f(r,z)-W(z,0)。

求解式(7)可得：

(8)

(9)

T(t)=Ae-λk,iCht

(10)

结合初始条件V(r,z,0)=f(r,z)-W(z,0)，将式(8)～(10)代入V(r,z,t)可得：

(11)

其中λk,i=αi2+nμk

Mi=Y0(αir)-Y0(αire)J0(αir)/J0(αire)

式中：αi(i=1,2,3,…)为特征方程J1(αirw)·Y0(αire)-J0(αire)Y1(αirw)=0的特征值；J0、J1分别为0阶和1阶1类Bessel函数；Y0、Y1分别为0阶和1阶2类Bessel函数。

依据u(r,z,t)=V(r,z,t)+W(z,t)可得式(1)的理论解：

u(r,z,t)=V(r,z,t)+zψ+φ

(12)

由式(12)可得t时刻平均固结度理论计算式为

(13)

2 工程实例

某试桩承载力实测值及其换算的平均固结度如表1所示[1,12]。

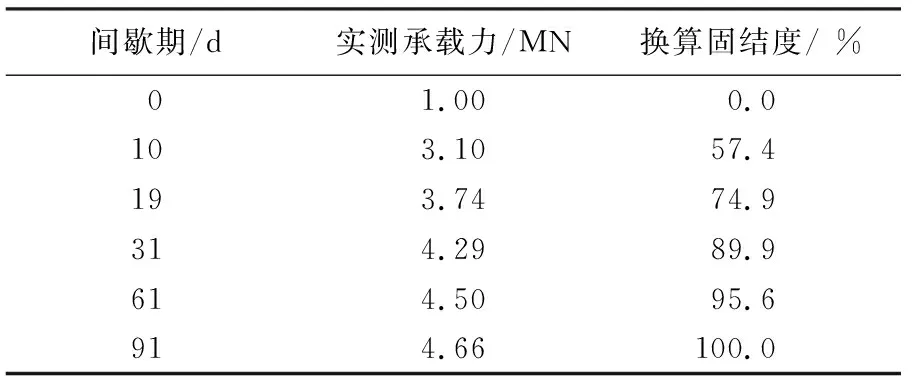
表1 承载力及平均固结度

f1(r,z)=βΔσ0+αfΔτ0

(14)

其中Δσ0=(Δσr+Δσθ+Δσz)/3

式中：Δσr、Δσθ、Δσz、Δτrz为沉桩引起的桩周土体的应力增量，由文献[1]确定；A为Skempton孔压参数；β为Henkel孔隙压力系数，对于饱和黏土β=1。

为便于比较及验证，也对式(13)所示的初始条件进行固结渗流问题计算：

f2(r,z)=γ′z

(15)

2.1 固结渗流计算

依据式(12),对水头和水力梯度为φ=3 m、ψ=-0.4和φ=3 m、ψ=0.4两种工况进行计算，绘制超静孔隙水压力等值线和渗流速度矢量如图2～5所示，图2和图4基于初始条件式(14)，图3和图5基于初始条件式(15)。由图2～5比较分析可知：固结开始时刻(0 d)，等值线及流速矢量的空间分布与初始条件吻合，验证了级数解答的正确性与收敛性；

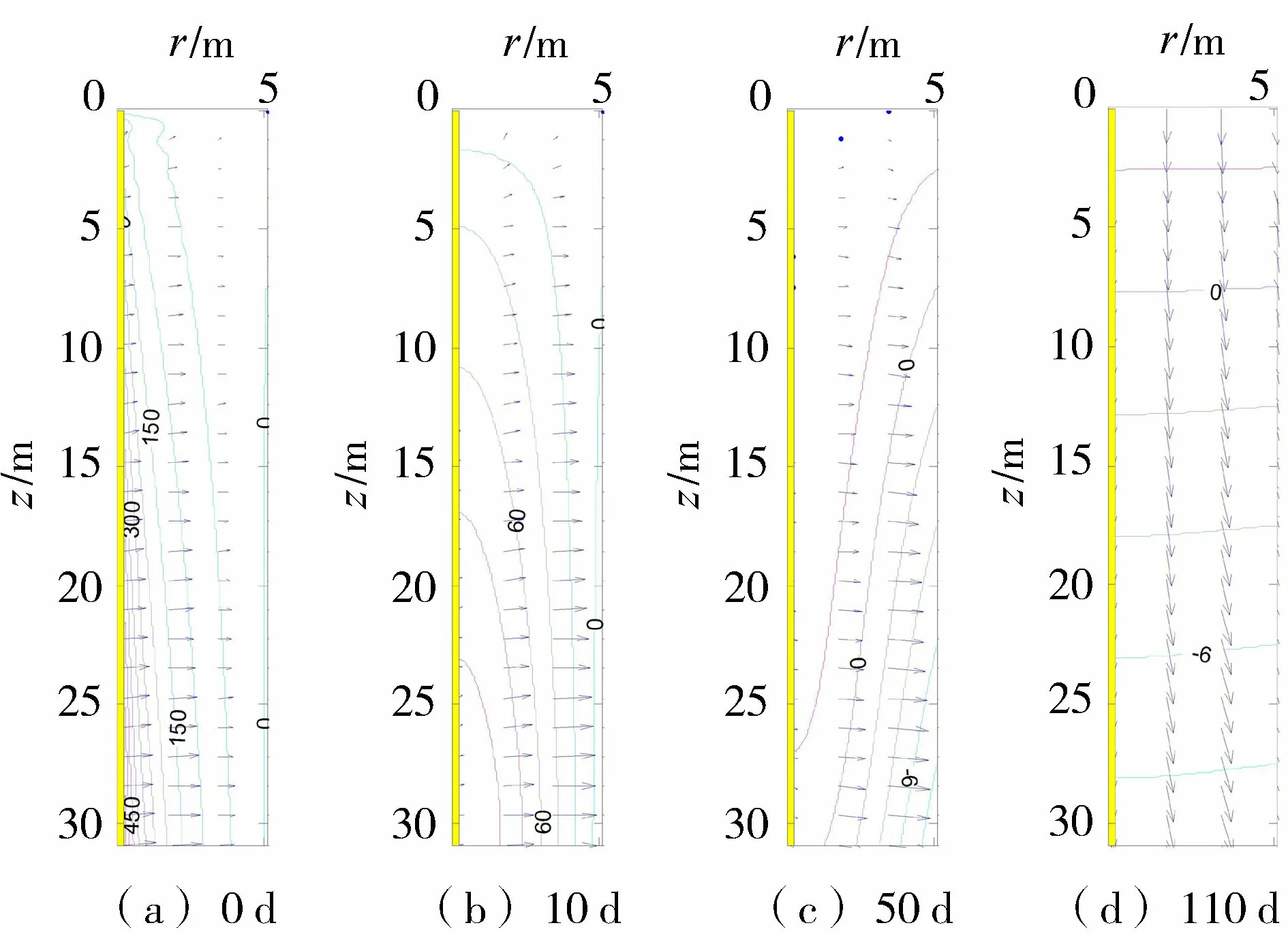
图2 超静孔隙水压力等值线(初始条件式(14)，φ=3 m，ψ=-0.4;单位：kPa)

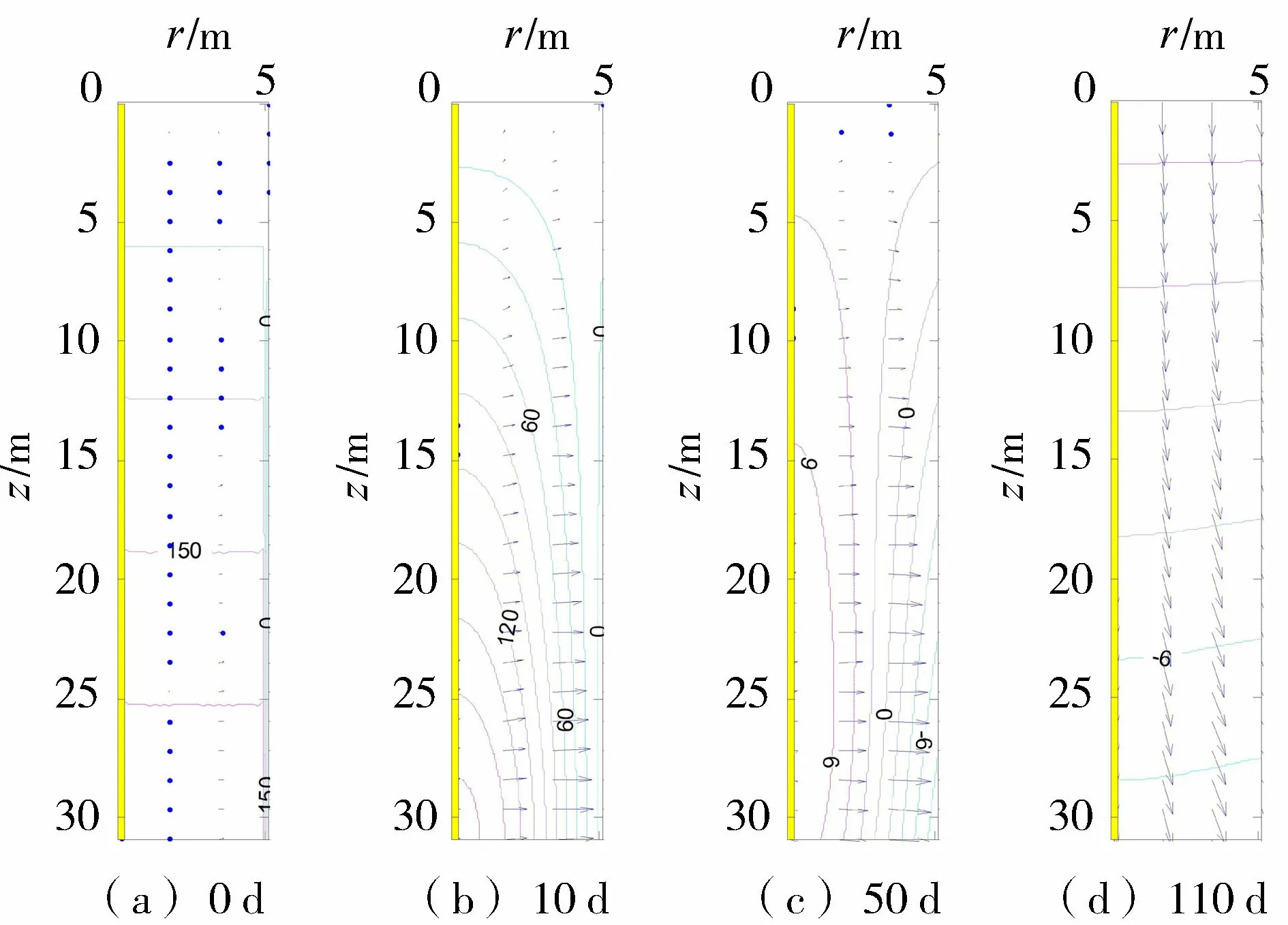
图3 超静孔隙水压力等值线(初始条件式(15)，φ=3 m，ψ=-0.4;单位：kPa)

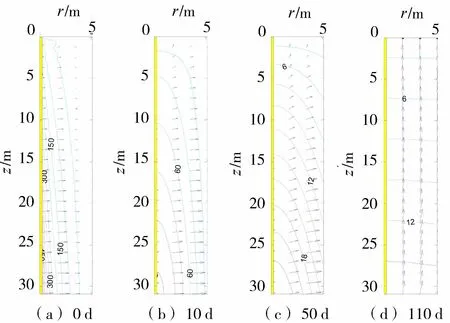
图4 超静孔隙水压力等值线(初始条件式(14)，φ=3 m，ψ=0.4;单位：kPa)

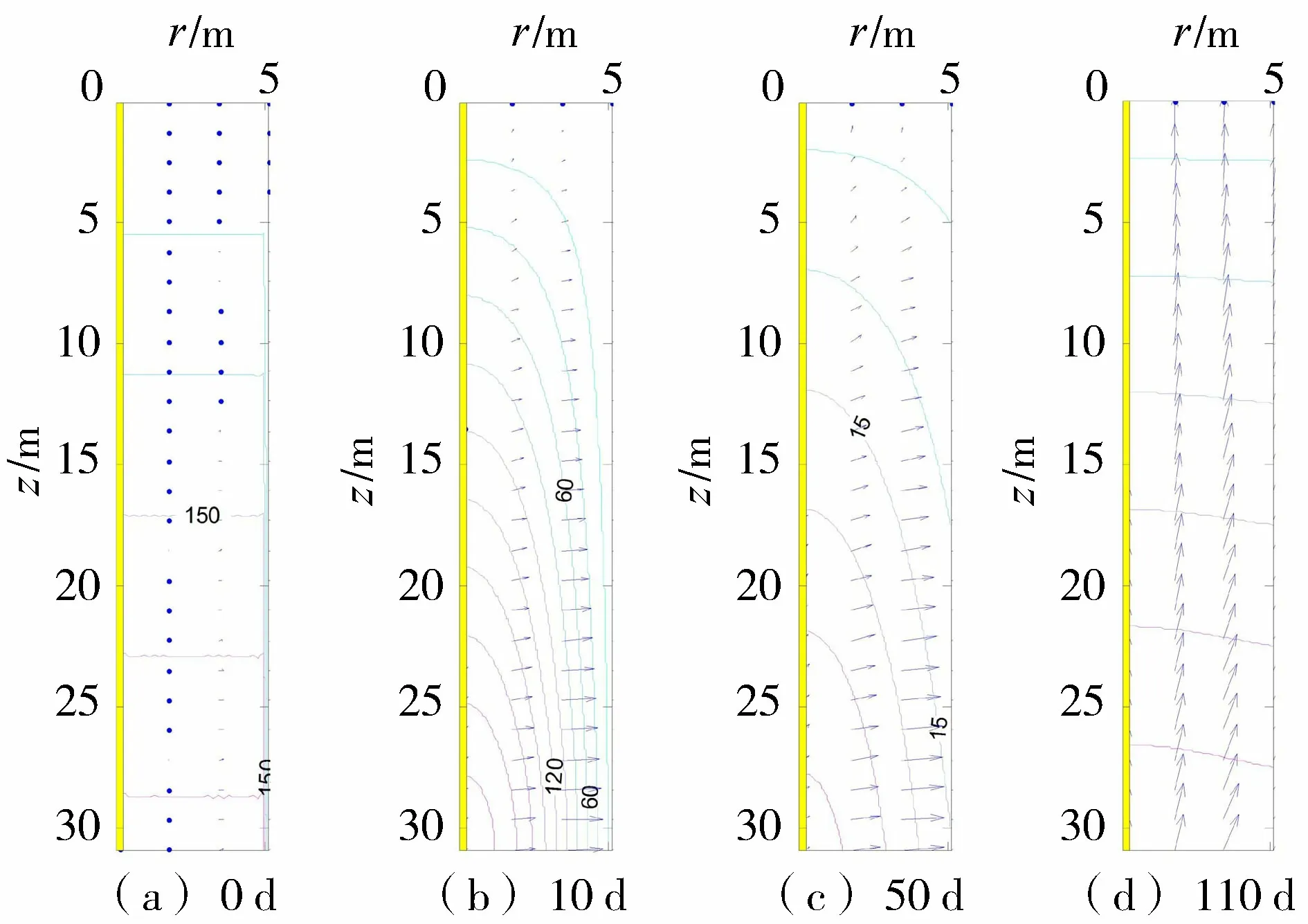
图5 超静孔隙水压力等值线(初始条件式(15)，φ=3 m，ψ=0.4;单位：kPa)

在固结稳定阶段(110 d)，等值线及流速矢量的空间分布由边界取值确定，为稳定渗流；固结渗流中间阶段(10～50 d)，渗流的空间分布和流速矢量的大小与方向受边界条件和初始条件共同作用，随时间变化，为非稳定渗流；负水力梯度将提高排水固结速度，并最终在桩周土中产生负超静孔隙水压力,即超固结，如图2和图3所示；正水力梯度的作用与负水力梯度相反，使土层的超静孔隙水压力无法完全消散，如图4和图5所示。

2.2 平均固结度计算

依据式(14)(15)对两种工况进行计算：地表水位分别为0 m、3 m、6 m和9 m且桩尖平面处水力梯度为0(隔水)的工况；地表水位6 m，且桩尖平面处水力梯度分别为-2/5、-1/5、0、1/5和2/5的工况。并结合表1所列固结度数据绘制图6和图7。

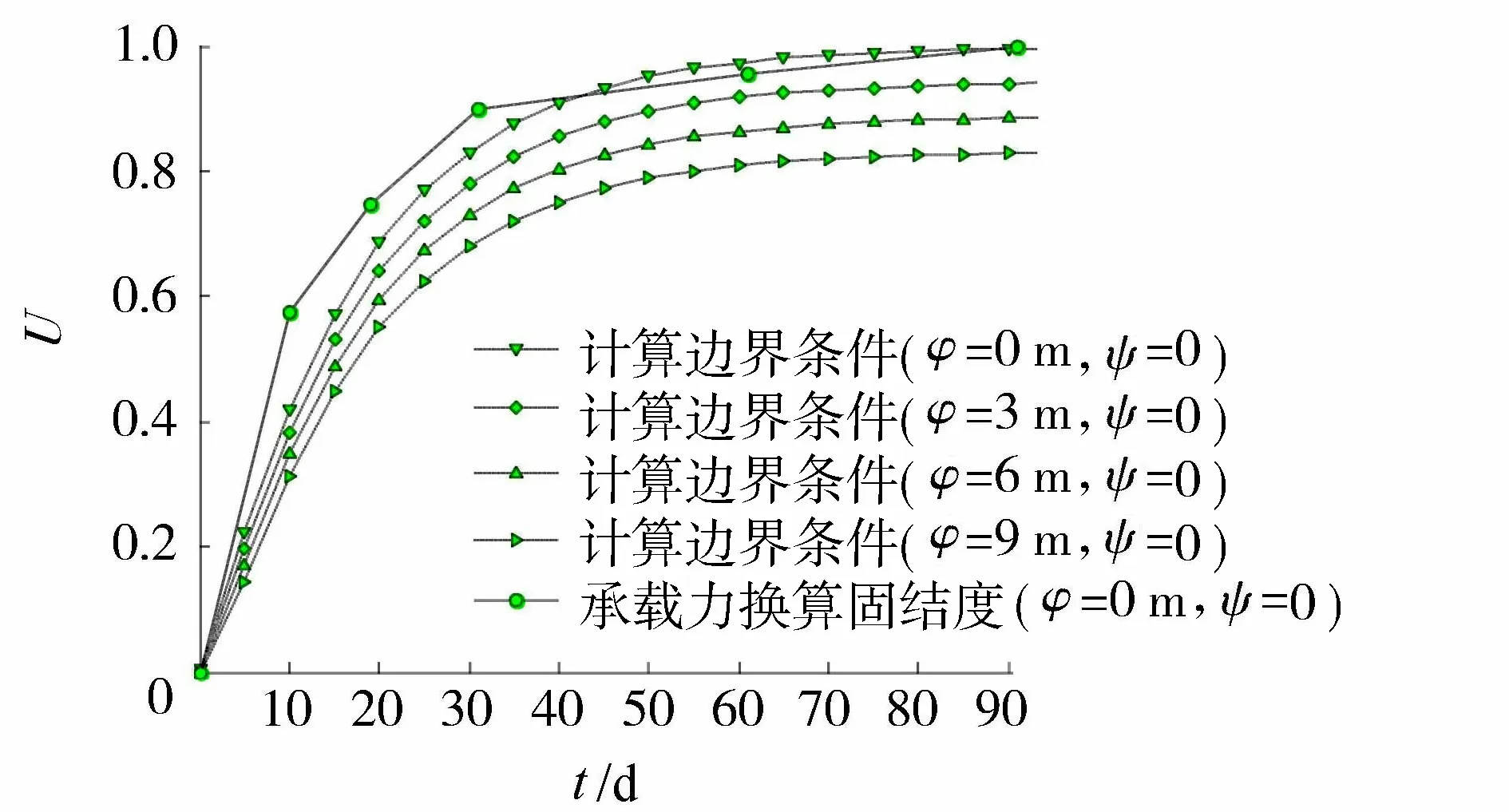
图6 桩尖平面水力梯度为0的时间-平均固结度曲线

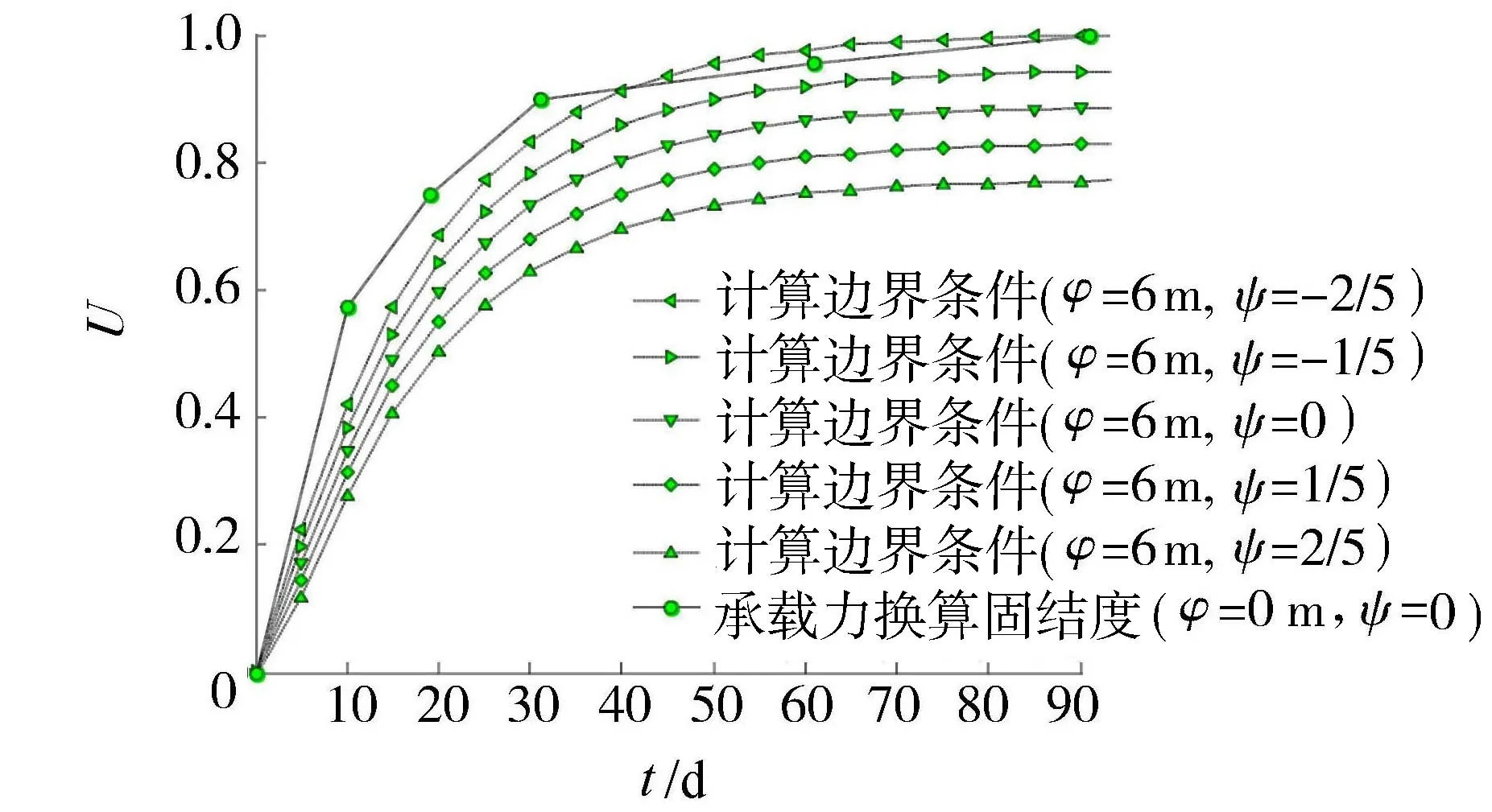
图7 地表水位保持6 m的时间-平均固结度曲线

由图6可知，对于地表水位为0 m的情况，计算所取边界条件与工程实例的边界相同，理论解答计算的固结度随时间变化规律也与实测承载力换算的固结度符合，验证了理论解答的正确性。

对于地表水位分别为3 m、6 m和9 m的情况，由于水位上升形成补给边界，同一时间点计算的平均固结度比0 m的情况降低。分析图6可知，对于50～70 d的时间区间，补给边界水位高每增加3 m(例如边界水头由0 m增加到3 m)，土层平均固结度值降低6%左右。

比较图6与图7可知，φ=6 m、ψ=-2/5与φ=0 m、ψ=0的理论计算固结曲线基本相同，说明φ=6 m与ψ=-2/5的补给与排水效果可以互相平衡，本文理论解答可以应用于抽水或回灌水量设计。

3 结 论

a.结合工程场地存在的各种渗流固结边界条件，建立空间轴对称、非齐次的定解条件，推导固结渗流和平均固结度计算理论公式。针对不同时刻、不同初始条件、不同边界条件，绘制桩周饱和黏土固结渗流水头等值线和流速矢量图，分析比较其时空变化规律，验证了解答的正确性与工程适用性。

b.应用实测试桩数据换算固结度，与本文理论解答计算结果进行对比，进一步验证了理论公式的正确性。

c.解答适用于具备稳定水头、水力梯度值或补给源的边界条件，适用于以抽水降压、加速固结或回灌减少地面沉降等为目的抽水或灌水量设计。